关于FPn-投射模

张健芳， 高增辉

（成都信息工程大学应用数学学院，四川成都610225）

在同调代数中，投射模、内射模和平坦模是基本且重要的研究对象.1970年，Stenström［1］引入FP-内射模的概念，并利用该内射模刻画了凝聚环.称一个右R-模M为FP-内射的，如果对每个有限表现右R-模F，都有Ext1R（F，M）＝0成立.相应地，右R-模M的FP-内射维数FP-idR（M），定义为使Extn+1R（F，M）＝0的最小正整数n；如果这样的n不存在，那么记为FP-idR（M）＝∞.进而定义环R的右整体FP-内射维数为r.FP-dim（R）＝sup｛FP-idR（M）｜M是一个右R-模｝.对任意非负整数n，称一个右R-模是有限n-表现的，如果存在一个右R-模的正合列Pn→Pn-1→…→P0→M→0，其中每个Pi是有限生成的投射模［2-3］.1994年，Costa［2］利用有限n-表现模类定义并研究了n-凝聚环（即环R称为右n-凝聚，若每个有限n-表现右R-模是有限（n+1）-表现）.1996年，Chen等［4］定义了n-FP-内射与n-平坦模，并且给出n-凝聚环一些类似于凝聚环的很好的刻画.

2003年，周德旭［5］引入FPn-内射与FPn-平坦模的概念，并利用它们刻画了右n-凝聚环.称一个右R-模M为FPn-内射模，若对任意的有限n-表现右R-模P，有Ext1R（P，M）＝0.2017年，Bravo等［3］也定义了FPn-内射模和FPn-平坦模的概念，讨论与有限n-表现模和n-凝聚环相关的相对同调性质，得到许多很好的刻画.2005年，Mao等［6］引入并研究模与环的FP-投射维数.设M是右R-模，记fpd（M）＝inf｛n｜Extn+1R（M，N）＝0，N是任意FP-内射右R-模｝，称为M的FP-投射维数.若不存在这样的n，则规定fpd（M）＝∞.特别地，若fpd（M）＝0，则称M为FP-投射模.环R的右FP-投射整体维数定义为

rfpD（R）＝sup｛fpd（M）｜M是一个有限生成右R-模｝.随后，FP-投射模及FP-投射维数受到了广泛关注和研究［7-9］.受文献［3］和［5］的启发，对任意整数n≥0或n＝∞，引入FPn-投射模和模的FPn-投射维数的概念，并利用它们给出右n-凝聚环一些新刻画.

下面所讨论的环均指有单位元的结合环，模指酉模，采用的术语和符号都是标准的［10-14］.

1 预备知识

下面将给出本文所需要的一些基本概念和结果.

定义1.1［2］称右R-模P为有限n-表现模，若存在一个右R-模的正合列

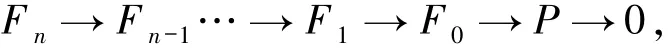
其中每个Fi是有限生成自由模（等价地，投射模）.

注1.21）由定义易知，对任意的n∈N，每个有限生成投射模都是有限n-表现的，且右R-模M是有限0-表现模（有限1-表现模）当且仅当它是有限生成的（有限表现的）.

2）记所有n-表现右R-模组成的模类为FPn，则有在文献［15-16］中，FP∞也称为超有限表现模类.

3）由定义可知，每个有限（n+1）-表现右R-模都是有限n-表现的，但反之未必.如果每个有限n-表现右R-模是有限（n+1）-表现的，则环R称为右n-凝聚环［2］.

定义1.3［3，5］称右R-模M为FPn-内射模，若对任意的有限n-表现右R-模P，均有

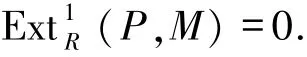
注1.41）由定义知，右R-模M是FP0-内射模（FP1-内射模）当且仅当它是内射模（FP-内射模）.

2）用FPn-Inj表示所有FPn-内射右R-模组成的模类，则容易得到）对于n＝∞时，文献［16］和［17］分别独

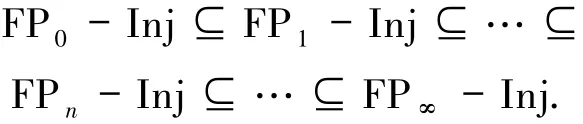
3立研究了FP∞-内射模的同调性质，FP∞-内射模也被称为弱内射模以及absolutely clean模.

Ng［18］定义了模与环的有限表现维数，即

定义1.5［18］设M是一个右R-模，定义M的有限表现维数为f.p.dim（M）＝inf｛n｜存在一个右R-模的正合列Pn+1→Pn→…→P0→M→0，其中每个Pi是投射模，且Pn+1，Pn是有限生成的｝.若这样的n不存在，则记f.p.dim（M）＝∞.

令r.f.p.dim（R）＝sup｛f.p.dim（M）｜M是有限生成右R-模｝为环R的右整体有限表现维数.

定义1.6［6］设M是一个右R-模，记为--内射右R模｝，称之为M的FP投射维数.若这是任意FP-样的n不存在，则规定fpd（M）＝∞.特别地，若fpd（M）＝0，则称M为FP-投射模.

记rfpD（R）＝sup｛fpd（M）｜M是一个有限生成右R-模｝，称为环R的右FP-投射整体维数.

引理1.7［6］设R是右凝聚环且M是一个右R-模，则有fpd（M）≤n当且仅当存在一个右R-模的正合列0→Pn→Pn-1→…→P1→P0→M→0，其中每个Pi是FP-投射的.

定义1.8［11］1）令F是一个右R-模类，M是一个右R-模.称同态φ：M→F为M的F-预包络，其中F∈F，若对任意同态f：M→F′，F′∈F，恒存在同态g：F→F′，使得gφ＝f.进而，若F＝F′且f＝φ时，还有同态g：F→F′是自同构，则称φ：M→F是M的F-包络.对偶地，可以定义M的F-（预）覆盖.

2）设F是一个右R-模类.令F⊥：＝对所有C∈F｝和对所有C∈F｝，分别称为F的右正交类和左正交类.

3）设A和B是2个模类.若A＝⊥B，且B＝A⊥，则称（A，B）为一个余挠对或余挠理论.进而，若每个模既有A-覆盖，又有B-包络，则称（A，B）为完备的（complete）余挠理论；若A对满同态的核封闭（等价地，B对单同态的余核封闭），则称（A，B）为遗传的（hereditary）余挠理论.

2 FPn-投射模

下面将引入FPn-投射模的概念，讨论该模类的一些基本性质，并利用它们刻画了右n-凝聚环.

定义2.1称一个右R-模M为FPn-投射模，若对任意的FPn-内射右R-模N，有Ext1R（M，N）＝0.用FPn-Proj表示所有FPn-投射右R-模组成的模类.

注2.21）因为所有的FPm-内射模都是FPn-内射的（n≥m），由定义可知，每个FPn-投射模是FPm-投射的，从而有

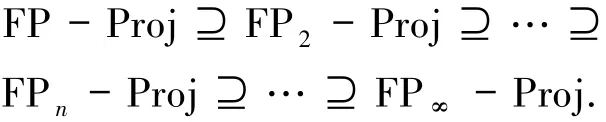
2）由文献［3］的推论4.2可知，（FPn-Proj，FPn-Inj）是一个完备余挠对.再根据文献［11］的定义7.1.5和定理7.4.1可得，每个右R-模都有特殊的FPn-内射预包络，即若M是任意右R-模，则存在一个右R-模的正合列0→M→C→F→0，其中C是FPn-内射模，F是FPn-投射模；对偶地，每个右R-模都有特殊的FPn-投射预覆盖.

3）对任意整数n≥1，一般情况下FPn-投射模未必是FPn+1-投射的.事实上，设R是一个2-凝聚但非凝聚的环，例如，设V是一个非Noether赋值环且rank（V）＞1，令R：＝V［［T］］为形式幂级数环，则由文献［2］的例4.4即知，R是2-凝聚环但不是凝聚的.现在设F是一个有限表现R-模.由定义2.1得F是FP-投射的.断定F必然不是FP2-投射的；若不然，假设F是FP2-投射的，由于R不是凝聚环，故由文献［5］的定理1可知，存在非FP-内射的FP2-内射R-模M，又根据注2.2的2），即知是得M是FP-内射模，这与M的选取矛盾.

命题2.3令｛Mi｝是一簇右R-模，则⊕Mi是FPn-投射模当且仅当每个Mi是FPn-投射模.

证明对任意的FPn-内射右R-模N，由同构知结论成立.

命题2.4设0→A→B→C→0是一个右R-模的正合列，其中C是FPn-投射模，则有：

1）若A是FPn-投射模，则B是FPn-投射的；

2）若B是FPn-投射模，则A是FPn-1-投射模.

证明1）由定义即知.

2）设M是FPn-1-内射右R-模，则存在右R-模的正合列0→M→E→N→0，其中E是内射模.由文献［5］的命题4可知，N是FPn-内射的.由于C是FPn-投射模，故由文献［3］的推论4.2知，Ext1R（C，N）＝0.又注意到每个FPn-1-内射模都是FPn-内射的，从而M是FPn-内射的.于是有下面的正合列

注意到

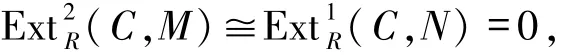
因而

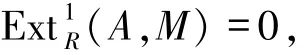
故A是FPn-1-投射模.

定义2.5若环R作为右R-模是FPn-内射的，则称环R为右自FPn-内射环.

下面的结论推广了文献［6］的命题2.9.

命题2.6令R是右自FPn-内射环，M是一右R-模，则以下条件等价：

1）M是FPn-投射模；

2）对任意右R-模正合列0→A→B→C→0，其中A是FPn-内射模，HomR（M，-）保持正合；

3）对每个右R-模正合列0→K→F→M→0，其中F是FPn-内射模，K→F是K的一个FPn-内射预包；

4）M是某一个FPn-内射预包K→F的余核，其中F是投射右R-模.

证明1）⇒2） 令0→A→B→C→0是一个右R-模的正合列，其中A是FPn-内射的，则由1）可知Ext1R（M，A）＝0.于是有HomR（M，B）→HomR（M，C）→0是正合列，从而2）成立.

2）⇒1） 设A是一个FPn-内射右R-模，且0→A→B→C→0是正合列，其中B为内射模，则有正合列

HomR（M，B）→HomR（M，C）→Ext1R（M，A）→0.再由2）有正合列HomR（M，B）→HomR（M，C）→0，所以Ext1R（M，A）＝0，故M是FPn-投射的.

1）⇒3） 设0→K→F→M→0是右R-模的正合列，其中F是FPn-内射模.对任意的FPn-内射右R-模N，由1）有Ext1R（M，N）＝0.于是0→HomR（M，N）→HomR（F，N）→HomR（K，N）→0是正合的，从而K→F是K的一个FPn-内射预包.

3）⇒4） 设0→K→F→M→0是一个右R-模的正合列，其中F是投射模.由于R是自FPn-内射环，可得F是FPn-内射的.再由3）即知K→F是K的一个FPn-内射预包.

4）⇒1） 由条件4），存在一个右R-模正合列0→K→F→M→0，其中F是投射模，K→F是K的一个FPn-内射预包.对任意的FPn-内射右R-模N，有正合列HomR（F，N）→HomR（K，N）→0.注意到HomR（F，N）→HomR（K，N）→Ext1R（M，N）→0是正合的，所以Ext1R（M，N）＝0，故M是FPn-投射模.

下面利用FPn-投射模的性质给出右n-凝聚环的一些等价刻画.

定理2.7对任意环R和任意整数n≥1，以下各条件等价：

1）R是右n-凝聚环；

2）FPn-Proj＝FP∞-Proj；

3）FPn-Proj＝FPn+1-Proj；

4）FPn-投射模类是可解的（resolving）；

5）（FPn-Proj，FPn-Inj）是遗传余挠对；

6）对每个k＞1以及任意N∈FPn-Inj和M∈

证明1）⇒2） 设R是右n-凝聚环，则由文献［3］的定理5.5可知FPn-Inj＝FP∞-Inj.再根据定义2.1，有

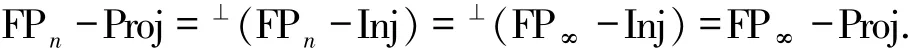
2）⇒3） 假设FPn-Proj＝FP∞-Proj.注意到FPn-Proj⊇FPn+1-Proj⊇…⊇FP∞-Proj，于是得FPn-Proj＝FPn+1-Proj，即3）成立.

3）⇒1） 设F是有限n-表现右R-模，且N是FPn+1-内射右R-模.由注2.2的3）即得，N∈（FPn+1-Proj）⊥＝（FPn-Proj）⊥＝FPn-Inj.于是有再由文献［3］的引理5.2，得F是有限（n+1）-表现的，从而得R是右n-凝聚环.

1）⇒6） 设M是一个FPn-投射右R-模，且N是一个FPn-内射右R-模，则有正合列0→N→E→Ω-1（N）→0，其中E是内射模，Ω-1（N）是N的第一次上合冲.再由文献［5］的命题4可知，Ω-1（N）是FPn+1-内射模.注意到R是右n-凝聚环，由文献［3］的定理5.5可得FPn-Inj＝FPn+1-Inj，故Ω-1（N）∈FPn-Inj.于是有下面的正合列

6）⇒4） 显然，每个投射模都是FPn-投射的.由命题2.4得FPn-投射模类关于扩张是封闭的.下面只需证FPn-投射模类对于满同态的核封闭即可.设0→K→F→M→0是一个右R-模的短正合列，其中M和F是FPn-投射模.对任意的FPn-内射右R-模N，有下面的正合列

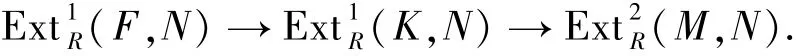
由于F∈FPn-Proj，N∈FPn-Inj，故0.又由6）得，因而即K是FPn-投射模.这就证明了FPn-投射模类是可解的.

4）⇒5） 由文献［3］的推论4.2可得（FPn-Proj，FPn-Inj）是一个完备余挠对.又由4）知FPn-投射模类是可解的，故有（FPn-Proj，FPn-Inj）是遗传余挠对.

5）⇒1） 由文献［3］的定理5.5即得.

3 FPn-投射维数

下面引入并刻画环与模的FPn-投射维数.

定义3.1设M是一个右R-模，对任意FPn-内射模N，则称使得成立的最小非负整数m为M的FPn-投射维数.用FPnpd（M）表示，如果不存在这样的m，则记FPn-pd（M）＝∞.令r.FPn-D（R）＝sup｛FPnpd（M）｜M是有限（n-1）-表现模｝，称环R的右FPn-投射整体维数.

显然，对任意右R-模M，有FPn-pd（M）≤pd（M），且在环R上r.FPn-D（R）≤r.D（R）.

命题3.2设R是右n-凝聚环，M是一个右R-模，则有

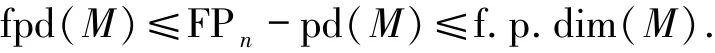
证明由于每个FPn-投射右R-模都是FP-投射的，故有fpd（M）≤FPn-pd（M），则只需证FPn-pd（M）≤f.p.dim（M）.不妨设f.p.dim（M）＝n＜∞，则存在右R-模的正合列Pn+1→Pn→…→P0→M→0，其中每个Pi是投射模，且Pn+1和Pn是有限生成的.令Kn-1＝Coker（Pn+1→Pn）.注意到Pn+1是有限（n-1）-表现的，则有Kn-1是有限n-表现的，从而有正合列0→Kn-1→Pn-1→…→P0→M→0，这里Kn-1是有限n-表现的.因此，对任意的FPn-内射模N，有

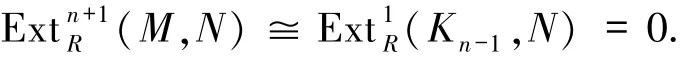
所以FPn-pd（M）≤n，即

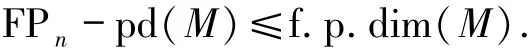
定理3.3设R是右n-凝聚环，n≥0，则对任意的右R-模M，以下各条等价：

1）FPn-pd（M）≤m；

2）对任意FPn-内射右R-模N与任意k≥m，有

3）对任意FPn-内射右R-模N）＝0；

4）对任意右R-模的正合列0→Pm→Pm-1→…→P1→P0→M→0，其中P0，P1，…，Pm-1是FPn-投射模，则Pm是FPn-投射的；

5）若0→Pm→Pm-1→…→P1→P0→M→0是右R-模的正合列，其中P0，P1，…，Pm-1是投射模，则Pm是FPn-投射的.

证明1）⇔2） 由定义直接可得，且2）⇒3）和4）⇒5）是显然成立的.

3）⇒2） 对任意的FPn-内射右R-模N，则存在一个右R-模的正合列0→N→E→Ω-1（N）→0，其中E是内射模，Ω-1（N）是N的第一次上合冲.根据文献［5］的命题4可知，Ω-1（N）∈FPn+1-Inj.注意到R是右n-凝聚环，又由文献［3］的定理5.5即得FPn-Inj＝FPn+1-Inj，则有Ω-1（N）∈FPn-Inj.设M是右R-模，考虑正合列

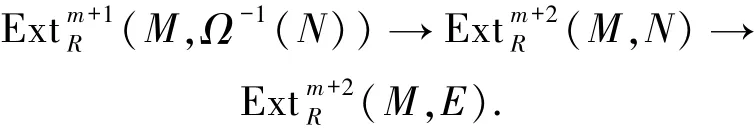
3）⇒4） 设0→Pm→Pm-1→…→P1→P0→M→0是右R-模的正合列，其中P0，P1，…，Pm-1是FPn-投射模.令

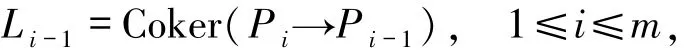
对任意的FPn-内射右R-模N，有正合列

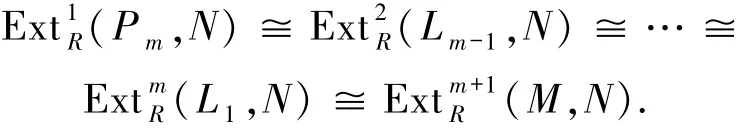
5）⇒3） 设0→Pm→Pm-1→…→P1→P0→M→0是右R-模的正合列，其中P0，P1，…，Pm-1是投射模.令Li-1＝Coker（Pi→Pi-1）（1≤i≤m）.对任意FPn-内射右R-模N，则有下面的同构由5）知，Pm是FPn-投射的，则从而故3）成立.下面利用FPn-投射模来刻画右FPn-投射整体维数为0的环.

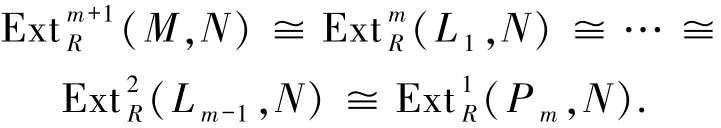
定理3.4对任意环R，以下条件是等价的：

1）r.FPn-D（R）＝0；

2）环R是（n-1）-凝聚环；

3）每个FPn-内射右R-模是FPn-1-内射的；

4）每个FPn-1-投射右R-模是FPn-投射的.

证明1）⇒2） 设M是有限（n-1）-表现右R-模.由1）可知FPn-pd（M）＝0，即M是FPn-投射模.对任意FPn-内射右R-模N，有Ext1R（M，N）＝0.由文献［3］的引理5.2得M是有限n-表现模.

2）⇒1） 对任意的有限（n-1）-表现右R-模M，由2）即知M是有限n-表现模.设N是一个FPn-内射右R-模，则有Ext1R（M，N）＝0，故M是FPn-投射右R-模，即FPn-pd（M）＝0.

2）⇔3） 由文献［5］的定理1即知.

3）⇒4） 令M是FPn-1-投射右R-模.对任意FPn-内射右R-模N，由3）知N是FPn-1-内射的.再利用文献［3］的推论4.2可得Ext1R（M，N）＝0，所以M是FPn-投射右R-模.

4）⇒3） 设N是FPn-内射右R-模，M是FPn-1-投射右R-模，则由4）可知，M是FPn-投射的.由文献［3］的推论4.2有Ext1R（M，N）＝0，故N是FPn-1-内射模.

引理3.5设R是一个右（n-1）-凝聚环，0→A→B→C→0是一个右R-模的正合列，则有：

1）若A、B和C中有2个模的FPn-投射维数有限，则第3个也有限；

2）FPn-pd（A）≤max｛FPn-pd（B），FPnpd（C）-1｝；

3）FPn-pd（B）≤max｛FPn-pd（A），FPnpd（C）｝；

4）FPn-pd（C）≤max｛FPn-pd（B），FPnpd（A）+1｝.

证明利用1）和定理3.3可知，这里2）-4）的证明与文献［10］的引理9.26的证明类似，只需证1）和2）.

1）设…→F1→F0→A→0和…→Q1→Q0→C→0分别是A和C的投射分解.由文献［10］的引理6.20，即马掌引理可得下面的交换图：

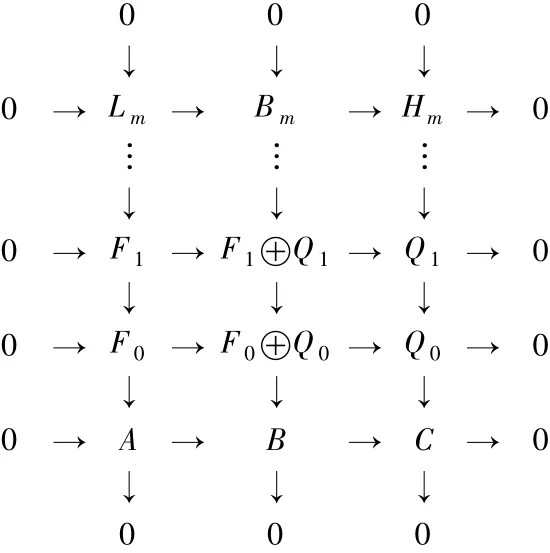
分成如下3种情形讨论：

情形1： 若对某个正整数m，有FPn-pd（A）≤m且FPn-pd（C）≤m，则由定理3.3可知Lm和Hm是FPn-投射模.再利用命题2.4即得Bm是FPn-投射的，故FPn-pd（B）≤m.

情形2： 若对某个正整数m，有FPn-pd（B）≤m且FPn-pd（C）≤m，则Bm和Hm是FPn-投射模.又由命题2.4知Lm是FPn-1-投射的.注意到R是右（n-1）-凝聚环，再利用定理3.4即知Lm是FPn-投射的，从而FPn-pd（A）≤m.

情形3： 若对某个正整数m，有FPn-pd（A）≤m且FPn-pd（B）≤m，则Lm和Bm是FPn-投射模.根据定理3.3得FPn-pd（Hm）≤1，从而FPn-pd（C）≤m+1.

2）令FPn-pd（B）＝n，FPn-pd（C）＝s且s＞n，则对任意FPn-内射右R-模N，有正合列

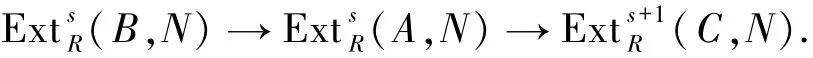
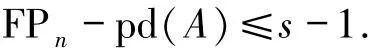
这就证明了

FPn-pd（A）≤max｛FPn-pd（B），FPn-pd（C）-1｝.

命题3.6对于环R，考虑下列各数量：

1）sup｛FPn-pd（M）：M是一个右R-模｝，

2）sup｛id（N）：N是一个FPn-内射右R-模｝，

3）sup｛FPn-pd（N）：N是一个FPn-内射右R-模｝；

则有3）≤1）＝2），当R是右（n-1）-凝聚环时，三者数量相等.

证明3）≤1） 显然.

1）≤2） 不妨设sup｛id（N）：N是一个FPn-内射右R-模｝≤m＜∞.对任意的FPn-内射右R-模N和任意右R-模M，由于id（N）≤m，故有因而FPn-pd（M）≤m.

2）≤1） 设sup｛FPn-pd（M）：M是一个右R-模｝≤m＜∞.令M是任意右R-模且N是FPn-内射右R-模，则由假设知FPn-pd（M）≤m，即有，故id（N）≤m.

1）≤3） 假设sup｛FPn-pd（N）：N是一个FPn-内射右R-模｝≤m＜∞且M是任意右R-模.由注3.2可知，存在一个右R-模正合列0→M→E→L→0，其中E是FPn-内射模，L是FPn-投射模.由于R是右（n-1）-凝聚环，利用引理3.5的2）可得FPn-pd（M）≤FPn-pd（E）≤m，故结论成立.

推论3.7设R是（n-1）-凝聚环，则以下各条等价：

1）每个右R-模是FPn-投射的；

2）每个FPn-内射右R-模是内射的；

3）每个FPn-内射右R-模是FPn-投射的.