基于深度学习的桥梁健康监测数据有效性分析

梁宗保，柴 洁， 纳守勇，马天立，唐 玉

(1. 重庆交通大学 信息科学与工程学院，重庆 400074； 2. 重庆忠万高速公路有限公司，重庆 401147)

0 引 言

建立四通八达的现代化交通网，大力发展交通运输事业，对发展国民经济，促进文化交流和巩固国防等方面都具有非常重要的作用。桥梁是交通的重要组成部分，桥梁安全问题是在役桥梁的核心问题。通过桥梁结构健康监测系统可以实时了解桥梁结构状态，对桥梁进行有效维护，延长桥梁的使用寿命。

桥梁结构健康监测系统包含信息获取与安全评价两个环节[1]，信息获取环节以多种类型的传感器及相关仪器组成的硬件系统为主。桥梁结构健康监测系统中数据有效性问题大多是由信息获取环节的硬件设备造成的。监测设备出现故障，无法为后续的安全评价提供正确的原始信息，从而对评价结果产生严重影响，导致桥梁结构事故预兆的漏报或误报。因此，传感器采集的原始信息有效性问题是桥梁结构健康监测系统面临的重大科学技术问题。

国内外相关研究都集中在异常数据分析、桥梁安全评估等方面，对桥梁结构健康监测数据有效性分析的研究较少。胡顺仁等[2]采用主成分分析法，结合关联稳态模型分析，通过统计过程控制限和T2控制限的计算发现失效数据点；黄晓微等[3]提出了一种基于K最近邻的传感器有效度算法，并将该算法应用于攀枝花倮果大桥健康监测系统的挠度数据分析；袁慎芳等[4]利用超球面一类支持向量机，结合核主成分分析，成功识别常规监测数据和特殊事件数据。但这些方法都是根据数据的统计特性识别单点失真数据，需要大量的领域知识，不能直接用于判断数据的有效性。

近年来，深度学习(deep learning, DL)在人工智能领域取得了重大成果。DL由G. E. HINTON等[5]在2006年提出，DL模型由多层非线性运算单元组合而成，将较低层的输出作为更高一层的输入，通过这种方式自动地从大量训练数据中学习抽象的特征表示，发现数据的分布特征。 DL因在特征提取与处理方面的优势在计算机视觉[6]、语音识别[7-8]与自然语言处理[9]等领域应用广泛。DL在桥梁健康监测系统中也发挥着重要作用。梁宗保等[10]提出了一种基于DL的桥梁结构健康诊断方法，将自编码器、支持向量机(support vector machine, SVM)相结合，采用5层网络对桥梁结构健康进行诊断；冯微等[11]针对车撞桥墩过程中桥墩受损等级不易被实时监测和预警的问题，构建了基于DL的桥墩损伤等级判别模型；S. CHEN等[12]提出了一种多分辨率自适应图滤波分类方法，通过半监督学习标记信号并将该方法间接应用于桥梁结构健康监测。但在监测数据有效性分析中，DL尚未得到广泛应用，鉴于DL具备从复杂数据中提取数据特征、学习数据分布的能力，可以将DL应用于桥梁健康监测数据有效性分析。

桥梁由不同的结构体组成，斜拉桥同一结构体各测量点间呈现位置上的关联[2]，同一时刻受到同一外部作用时，同截面和相邻测量点的数据保持高度关联。针对上述特性，提出了一种灰色关联度与DL相结合的方法，通过灰色关联分析(grey relation analysis, GRA)对数据进行预处理，自动给定数据标签并进行标签正确性验证，结合DL模型深度神经网络(deep neural network, DNN)、深度信念网络(deep belief network, DBN)对数据有效性进行分析，提高模型预测效率，实现了监测数据有效性的智能分析。

1 DNN与DBN

1.1 DNN

DNN是输入层和输出层之间有多个隐藏层的人工神经网络(artificial neural network, ANN)，DNN通过学习来存储输入与输出间的复杂映射关系。DNN中单个神经元为感知机模型，模型结构如图1。感知机模型是生物神经细胞的简单抽样，模型输出是输入经过线性变换与函数激活的结果。神经元上的计算为：

(1)

式中：x为模型输入；w为权重；b为偏置；Z为线性运算结果；f()为激活函数，通常为tanh()或sigmoid()函数；y为神经元输出。DNN的学习是基于损失函数最小化的，通过反向传播算法最小化假设函数与实际值间的距离，迭代优化w与b。

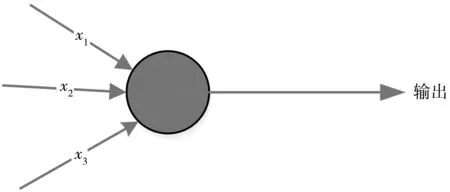
图1 感知机模型

DNN通过叠加多层感知机，解决了浅层神经网络非线性拟合不佳的问题。对于非线性的复杂数据，DNN能自动提取数据特征，具有较高的预测精度。

1.2 DBN

受限玻尔兹曼机(restricted boltzmann machines, RBM)是包含一层可见单元和一层隐藏单元的无向概率图模型，层间全连接，层内无连接，其结构如图2。DBN是由多个RBM累叠所得，且具有若干隐藏变量层的生成模型。作为自编码器，DBN可以在尽量保留数据特征的情况下降低数据维度；作为分类器，DBN可以有效减少分类错误率。DBN的一种高效训练方式是将复杂模型看作是一组简单模型的组合序列，采用逐层无监督的方法学习参数[13]。

图2 RBM模型

DBN允许序列中的RBM接收不同的数据表示，且保持前一个RBM的输出为后一个RBM的输入，因此能够更好的学习数据分布，具有较高的分类性能。

2 数据有效性预测模型设计

DNN、DBN模型可以学习到刻画数据本质属性的特征，对数据分类任务有很大帮助[14]。以下利用DNN与DBN，建立用于分析桥梁结构健康监测系统传感器数据有效性的模型。

2.1 DNN模型结构

建立用于桥梁结构健康监测数据有效性分析的DNN模型主要需要确定以下超参数：模型层数、输入层神经元个数、输出层神经元个数、隐藏层神经元个数。模型输入层神经元个数一般等于输入的数据序列长度，输出层神经元个数为分类任务的类别数。参考Kolmogorov定理，结合对比实验，确定模型层数及神经元个数。模型结构如图3，图中数据为该层内神经元个数。

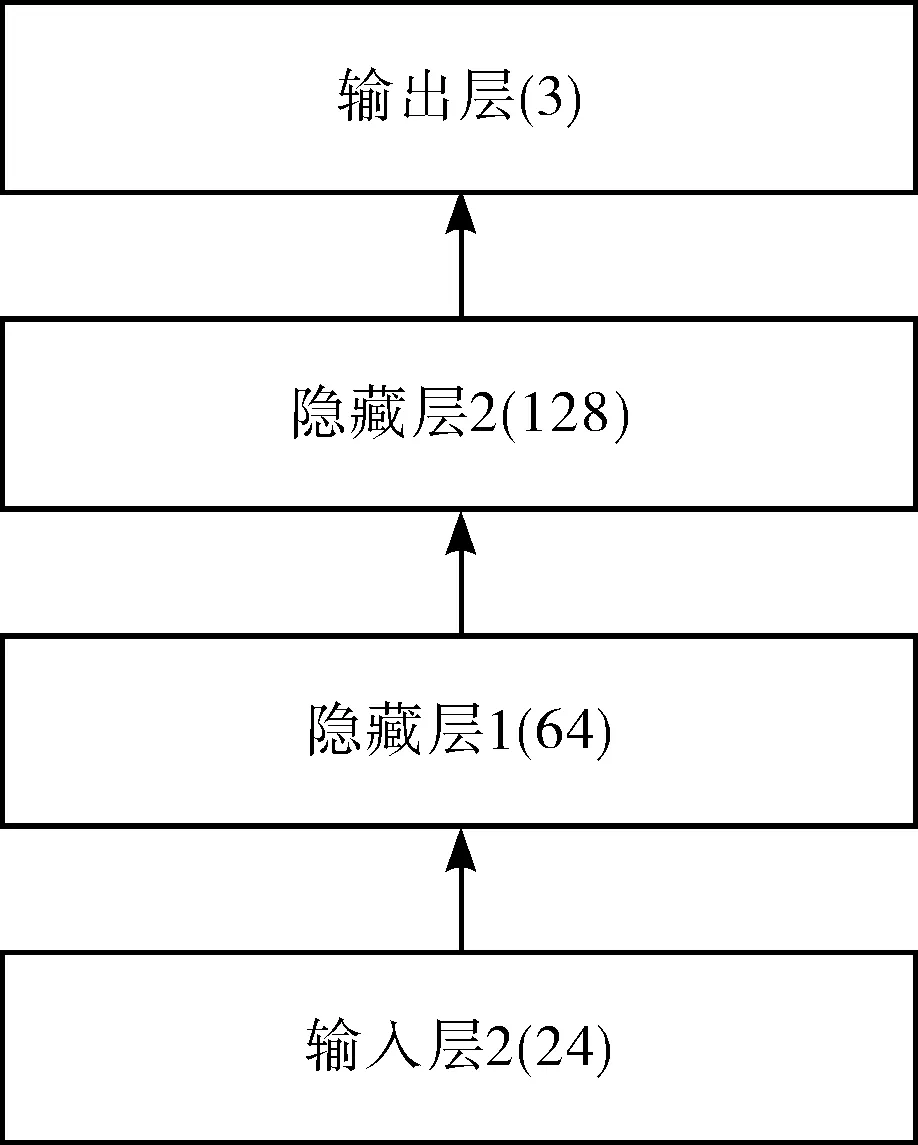
图3 DNN模型结构

模型损失函数采用交叉熵函数：

h0(xi)]

(2)

式中：h0(xi)为输入xi时DNN的输出；yi为样本标签；N为样本个数。

反向传播过程中计算公式为：

(3)

式中：α为学习率。

模型输出与数据段类型对应关系如表1。模型训练过程：利用权重系数矩阵w与偏置向量b和输入向量x进行前向传播得到模型输出；计算模型输出与标签间的损失函数；通过反向传播算法最小化损失函数，优化模型参数，提高模型性能。

表1 模型输出结果对应关系

2.2 DBN模型结构

建立用于桥梁结构健康监测数据有效性分析的DBN模型，模型由两个RBM堆叠而成。模型输入层神经元个数与输入序列长度一致，模型结构如图4，图中括号内为单层神经元个数。模型训练过程采用对比散度算法[15]，详细流程如1)至4)：

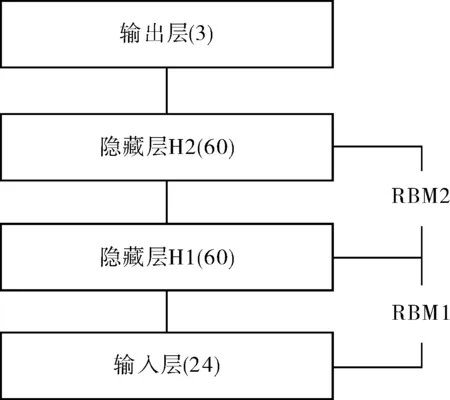
图4 DBN模型结构

1)将输入赋值给可见层v，计算隐藏层中每个神经元被激活的概率p(h1|v1)。隐藏层中神经元hj被激活的概率为：

(4)

式中：hj=1为神经元处于激活状态；f()为激活函数；bj为j的偏置；vi为可见层神经元i的输入；wij为i与j间的权重。

2)利用Gibbs采样，从已得到的概率分布中抽取一个样本：h1～p(h1|v1)。

3)通过h1实现可见层的重构，利用隐藏层反推可见层中神经元被激活的概率p(v2|h1)。可见层中神经元vi被激活的概率为：

(5)

式中：ci为i的偏置。

4)同2)，抽取一个样本v2～p(v2|h1)，用v2计算隐藏层神经元激活概率p(h2|v2)并更新参数为：

(6)

式中：w为权重；b、c分别是可见层和隐藏层的偏置；λ为学习率。

模型训练过程如下：将输入层和隐藏层H1作为第1个RBM，训练RBM的参数，然后固定参数，将H1作为可见层，H2作为隐藏层，训练第2个RBM，逐层训练每一个RBM，最后通过有监督的反向传播算法微调网络中每层之间的权重，进一步优化网络。

3 无效数据段特征分析与数据集构建

对桥梁结构健康监测数据进行特征分析的主要目的是研究数据的分布特征，进一步对数据进行分析与处理。目前桥梁结构健康监测数据的特征分析大多针对单点数据，但在实际应用中，单点与数据段之间存在一定的关联，一个无效数据段必然包含无效数据点，单个数据点的失效也会导致数据段的失效，因此在数据特征分析的基础上针对数据段进行处理，主要方法如下：首先根据无效数据段常见特征标记数据段，然后结合桥梁挠度传感器节点布置情况根据GRA[16]对数据有效性进行分类，构建数据集。

3.1 无效数据段特征分析

数据段失效可能是连续的数据点失效，也可能是单个数据点异常。无效数据一般存在两种情况：超过阈值且无法恢复的数据；因传感器故障而产生震荡的数据。

无效数据段常见的特征如下：①漂移失效：在斜拉桥监测中，正常情况下，测点数据在一段时间内的幅值变化具有一定规律，如果某段时间内，数据幅值呈现连续小幅恒定增加或小幅恒定减小的漂移变化，则此段数据为漂移失效；②数据频率异常：正常情况下桥梁结构健康监测数据按照一定的频率波动，无效数据可能出现波动异常；③恒值失效：传感器因故停止工作或输出不变，可能导致某一时间段内数据为恒定值；④数据段跳变：相比原有数据，某段数据的波动特征变化不明显，但幅值出现较为明显的增加或减少。

3.2 数据集构建

根据3.1节中无效数据段常见特征能够对数据段进行可视化标记，但很大一部分无效数据段的变化处于合理的范围内，没有表现出可视化的常见无效特征，因此不能直接标记。鉴于斜拉桥同截面与相邻节点的数据存在高度关联的特性，可利用关联性分析来标记无效数据段。

关联性分析是一种能够可视化地定量地说明事物或参数之间相互关系的方法，主要思路是通过比较一个样本数据序列和其他若干序列在不同维度上的相似程度来衡量序列间的紧密性。GRA是一种经典的多因素关联分析方法，主要研究对象是离散的数据状态变量，比如桥梁结构健康监测数据。在系统发展过程中，如果两个因素的变化趋势具有一致性，即同步程度较高，则认为两者关联较大；反之，则两者关联较小。斜拉桥结构特性表明，其相邻节点在荷载作用下的效应数据之间的关联性较强，而节点数据失效则会影响这种关联性。因此灰色关联度可以运用在斜拉桥挠度数据分析中，根据参考序列和比较序列间的动态关联关系判断监测数据是否有效。GRA标记数据的步骤如下：

1)确定数据列：将挠度传感器数据以天为单位切分为数据段，需要判断有效性的数据段为参考数据列，相邻和同截面节点的数据列为比较数据列。

2)数据标准化：对数据序列进行无量纲处理，转化为方差为0，标准差为1的数据序列。

3)计算关联系数：假设参考数据列X0和m个比较数据列X{Xi|i=1,2,……m}均有n维分量，关联系数的计算公式为：

ξoi(k)=

(7)

式中：ρ为分辨系数，取值一般在区间(0, 1)；k为第k维分量。

4)计算关联度：计算参考数据列在各个分量上的关联系数均值为：

(8)

式中：roi为关联度，反映了序列间的变化相似度。

5)判定参考数据列有效性：参照关联度常用强度判定[17]，结合斜拉桥结构力学理论分析及桥梁行业一般认定[2]，对数据序列进行有效性判定的标准如下：关联度0.8～1.0属于强关联，判定为有效数据段；0.8～0.6属于较强关联，判定为一般有效数据段；0.6以下属于弱关联，判定为无效数据段。判定结果标签设定如表2。

表2 数据处理结果对应关系

其中，有效数据段即能够真实反映桥梁节点结构状况的数据段，可直接用于后续的桥梁健康诊断。无效数据段即无法真实反映桥梁节点结构状况的数据段，不可用于桥梁健康诊断。而一般有效数据段即能够大致反映桥梁节点结构情况的数据段，需要进一步处理以确认其是否可用。例如通过修复其中的异常数据点，重新计算关联度来确定其是否为有效数据段。

采用上述判定标准对参考数据列与比较数据列的关联度均值进行判定，完成数据集的构建。

6)验证数据标签可信度：使用统计算法3σ、孤立森林和LOF算法对传感器数据进行单点异常分析，通过异常点在数据段所占比例验证标签可信度。

根据上述方法结合传感器布置位置对马桑溪大桥主梁挠度传感器数据进行特征分析与处理，构建数据集。马桑溪大桥挠度传感器节点布置如图5，图中节点标号与关联度计算中数据列标号对应。图6为数据段关联度计算结果示例。表3为数据集标签可信度验证结果。

图5 桥梁主梁传感器节点布置

4 实验与结果分析

4.1 数据集、度量方式与实现细节

在桥梁结构健康监测数据有效性分析中，使用第3部分的数据列构建数据集，判定结果为数据标签，表1为模型输出与数据标签间对应关系。将数据集以6∶2∶2的比例切分为训练集、验证集与测试集。采用交叉熵函数和准确度作为衡量指标。模型构建主要基于Keras与TensorFlow框架，选定规模为32的小批量RMSprop作为模型优化器，即反向传播算法。

表3 数据标签可信度

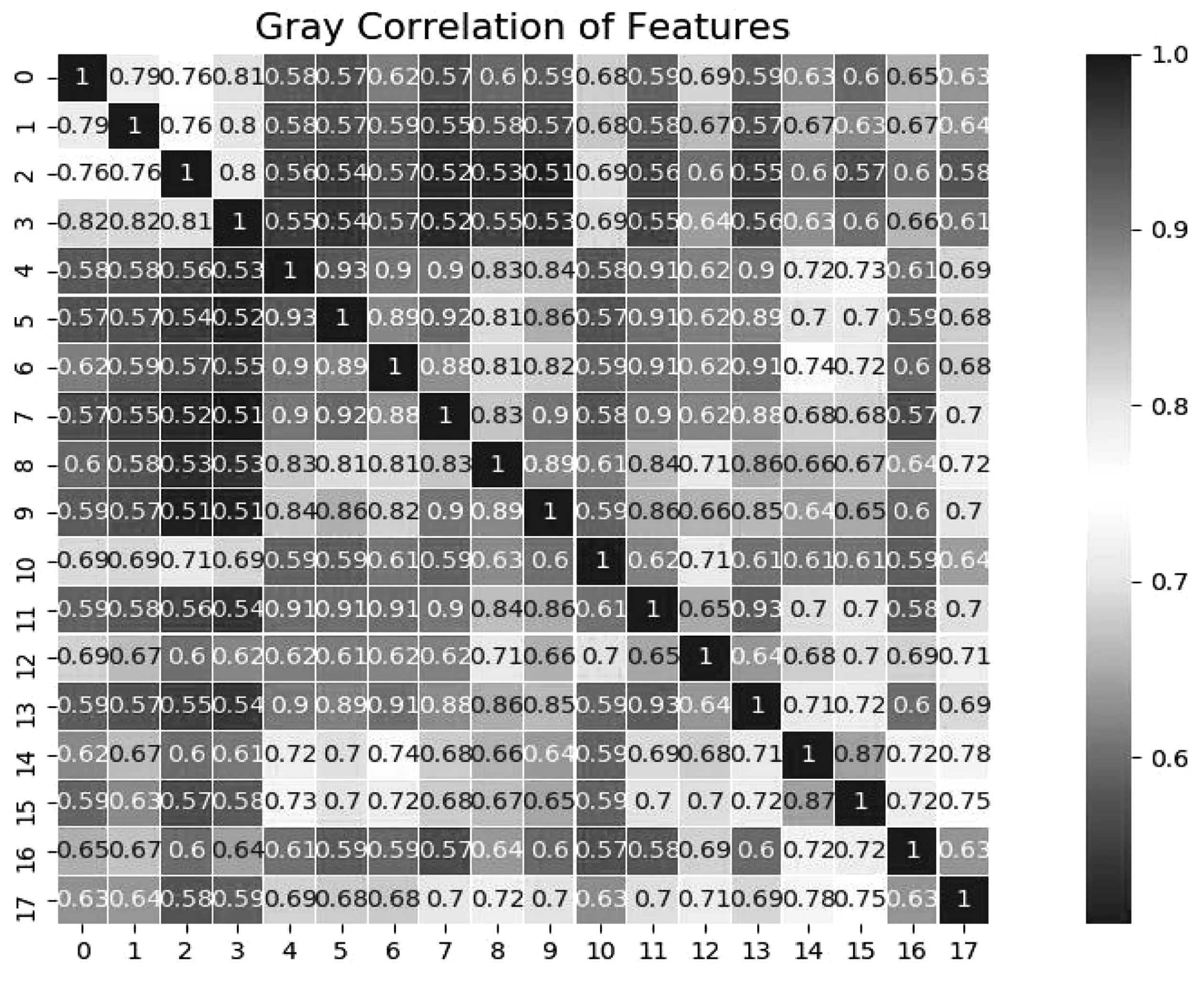
图6 关联度计算结果示例

4.2 实验与实验结果

基于Keras框架构建DNN模型，模型架构如图3，隐藏层选择修正线性单元(rectified linear unit, RLU)作为激活函数；输出层激活函数为Softmax函数；损失函数使用交叉熵函数；学习率0.05；迭代次数100。根据图4构建DBN模型，激活函数、损失函数、评价指标、迭代次数、学习率与DNN相同。

使用决策树(decision tree)、随机森林(random forest)、 SVM等机器学习分类方法进行对比实验，实验效果如表4。

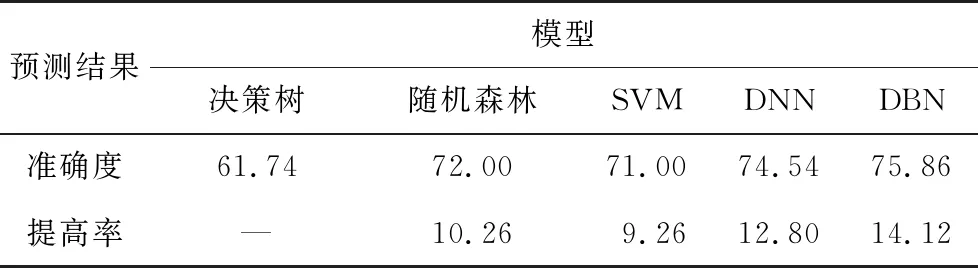
表4 模型预测结果对比

4.3 实验分析

将决策树、随机森林、SVM等多种经典机器学习算法与DNN、DBN模型进行对比实验，实验结果如表4。在相同数据集上，相比于决策树模型，DBN提高约14.12%的预测精度。实验证明，深度模型具备较强的数据分析与处理能力，更适用于桥梁健康监测数据有效性分析。

但DNN、DBN模型中存在大量参数，且参数初始值随机设定，因此在训练过程中容易陷入局部最优，影响网络模型训练及测试精度。结合人工萤火虫群优化算法(glowworm swarm optimization, GSO[18]，进一步优化DBN。GSO具有较好的解决优化问题的能力，将损失函数作为目标函数，采用GSO对RBM的初始参数进行优化，提高模型泛化性及测试精度。实验结果如表5，表中DBN-R表示参数随机初始化，DBN-GSO表示使用萤火虫算法优化初始参数。实验证明使用GSO算法进行模型参数初始化可以提高模型预测精度。

表5 模型优化结果

5 结 论

数据有效性分析对桥梁健康监测系统具有重要意义。基于斜拉桥结构特性，使用GRA对桥梁挠度传感器数据段有效性进行判断，结合多种异常检测算法对判断结果进行验证。以判定结果为数据标签，利用DNN、DBN模型进行训练，结合GSO与DBN，得出以下结论：

1)采用GRA衡量数据段间的相关性，能够自动给定数据标签并进行验证，为预测模型提供数据集。

2) 基于DL的数据有效性分析模型效果优于经典机器学习方法。相比于决策树，DBN模型预测准确度提高了14.12%，具有更高的预测精度与应用价值。

3)基于DBN-GSO的桥梁结构健康监测数据有效性分析模型预测精度达到了94.47%，验证了所提方法的有效性。