离场航空器滑行时间预测研究

李 楠，焦庆宇，张连东，樊 瑞

(1. 中国民航大学 空中交通管理学院，天津 300300； 2. 南京航空航天大学 民航学院，江苏 南京 211106)

0 引 言

机场运行效率对于整个空中交通系统至关重要。大型机场的场面运行错综复杂，地面交通流量大、密度高、协调难度大导致出现运行保障压力大的情况时有发生。航空器滑行时间预测的准确性对于优化航班推出时刻、提高机场地面运行效率及离场时隙的使用效率、减少空中交通网络延误的传播具有重要作用。在此驱动下，准确的预测航空器的离场滑行时间从而计算出合理的撤轮档时间，成为离场管理系统(DMAN)和机场协同决策系统(A-CDM)中离场时隙有效利用的重要前提。同时可以为航空公司准确计算油量、航空器减少地面排放提供理论参考。

国外学者对于滑行时间预测开展了广泛的研究。H. IDRIS等[1]基于多元线性回归算法对波士顿机场的航空器滑出时间进行预测，提出了场面航空器数量与航班滑行时间的关系；R. A. SHUMSKY[2]探讨了航空公司运行对滑行时间预测的影响；R. R. CLEWLOW等[3]继续细化了场面滑行航空器数量与滑行时间的关系，重点研究了进场滑行航空器数量与离场航班滑出时间的关系；S.RAVIZZA等[4]将滑行距离分为推出路段、转弯路段以及直线滑行路段，并对航空器经过这3个路段时的滑行转角、速度进行研究，运用多元线性回归算法建立预测模型；F. HERREMA等[5]运用多元线性回归、支持向量机、TSK模糊模型3种方法对滑行时间预测结果进行对比研究；H. LEE等[6]运用LINOS仿真软件对机坪推出时间及滑行时间进行仿真，并运用机器学习中的随机森林算法对计算机模拟的滑行时间与软件仿真的滑行时间准确率进行对比分析；A. E. I. BROWNLEE等[7]运用模糊系统算法和时间窗算法将确定性情况下滑行时间预测与滑行路径规划结合。

国内研究主要通过将滑行时间预测与滑行路径规划结合进行研究，而针对滑行时间的单独研究则较少。刘继新等[8]运用支持向量机-BP神经网络结合方法对滑行路径进行预测，在离场滑行时间的预测下对航班滑行路径进行优化研究；姚梦飞[9]运用长短期记忆模型和循环神经网络算法对航空器滑行路径进行预测，通过研究航空器以往的滑行轨迹坐标与速度从而预测未来的航空器位置；冯霞等[10]通过研究场面航空器数量来衡量场面拥挤情况，并基于此建立航空器滑出时间模型。

以上研究并未考虑跑道运行模式以及机场运行高峰与低谷时间对滑行时间的影响，造成跑道运行模式及时间段的变化下预测准确度降低的情况出现。笔者将跑道起降组合模式、高峰低谷时段运行加入到分析因素中，运用多元回归方法对滑行时间进行预测，得出最优的滑行时间预测模型。

1 数据描述

1.1 样本数据分析

笔者对首都机场2019年3月及2019年6—7月共计90 d的进离港航班进行统计分析，数据覆盖一周中的所有天及节假日。其中总数据为46 935条，由于7月2日及7月6日天气影响造成数据误差较大，这两天数据并未作为研究样本。原始数据信息由航班号、停机位、上轮档时刻、撤轮档时刻、起飞时刻、降落时刻组成。航空器样本数据集如表1。

表1 首都机场航空器样本数据

对获取的数据进行去噪声处理后得到样本总体滑行时间最大值、最小值、平均数、中位数、标准差如表2。

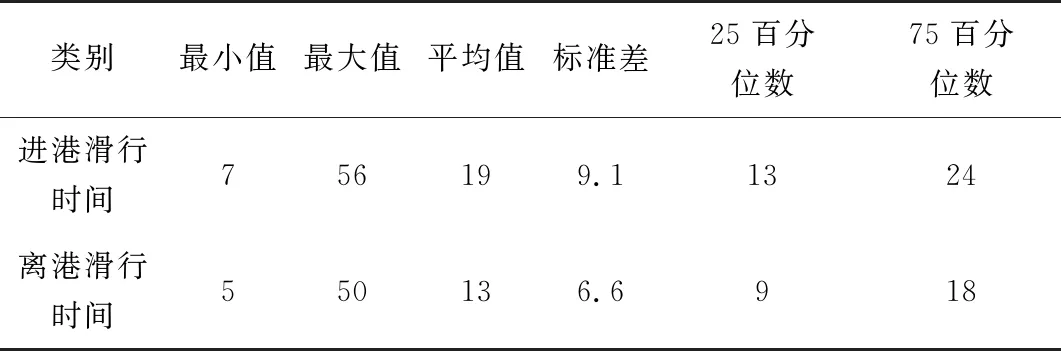
表2 航空器滑行时间统计分析

图1为北京机场航空器离场滑行时间频率分布。由图1可知，北京首都机场离场航空器滑行时间呈现右偏态分布，其偏度和峰度分别为1.26、2.74，进场航空器偏度和峰度分别为1.1、1.3。同时表2中的第25百分位数及第75百分位数表明，首都机场滑出时间集中在13～24 min，滑入时间集中在9～18 min，航空器滑出时间分布更集中，表明进场航空器滑行效率较离场航空器滑行效率更高。

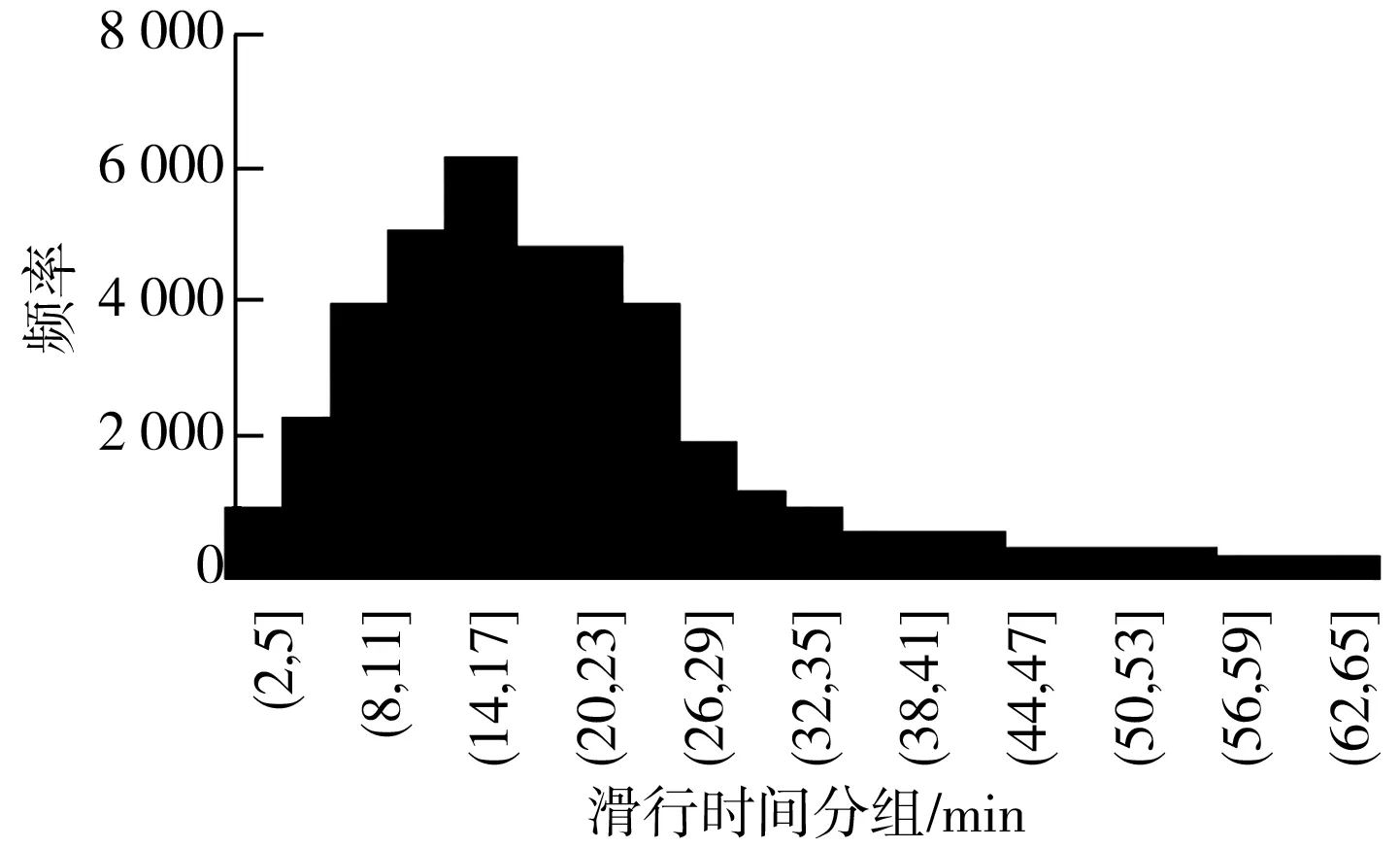
图1 首都机场离场航空器滑行时间分布

1.2 关键指标定义与分析

1.2.1 滑行时间

笔者参照中国民用航空局机场协同决策(A-CDM)系统中对航空器滑行时间的定义进行计算。

离场航空器滑行时间(Ttaxi-out)指航空器从撤轮挡时刻(Tblock-out)开始到起飞离地时刻(Tdeparture)为止的时间。离场滑行时间包括停机坪推出时间、滑行道滑行时间及跑道前等待时间，如式(1)：

Ttaxi-out=Tdeparture-Tblock-out

(1)

进场航空器滑行时间(Ttaxi-in)指航空器从落地(Tarrive)开始到滑入停机位停妥上轮挡时刻(Tblock-in)为止的时间，如式(2)：

Ttaxi-in=Tarrive-Tblock-in

(2)

1.2.2 滑行距离

首都机场为3条跑道及3个航站楼共同运行模式，进离场航空器共用滑行道及跑道，机场场面交通流复杂。实际运行中航空器滑行路径的选择并不是基于最短路径，与场面的滑行规则、停机位和使用跑道等相关。笔者引用了文献[11]中主流滑行路径的定义及机场航行资料(AIP)的滑行规则，将停机位与起飞跑道之间使用频率最多的滑行路径作为该机位主流滑行路径。通过统计一周的场面监视数据得出不同停机位与起飞跑道对应的主流滑行路径，计算主流滑行路径的距离，用其来作为航空器的滑行距离。

1.2.3 场面运动航空器数量

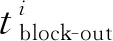
笔者引用R. R. CLEWLOW等[3]对离场的航空器数量的定义并进行研究，如式(3)：

(3)

同理，给出进场航空器数量的定义及解释，如式(4)：

(4)

针对于离场航空器i，如果航空器j的落地时间早于航空器i撤轮挡时间，同时航空器j的上轮挡时间晚于航空器i的撤轮挡时间，那么航空器j属于对航空器i滑行时间有影响的场面离场运动航空器，所有满足此条件的航空器数目表示为D1(i)；针对于离场航空器i，如果航空器j的撤轮挡时间要晚于航空器i撤轮挡时间，且早于航空器i起飞离地时间，那么航空器j属于对航空器i滑行时间有影响的场面离场运动航空器，所有满足此条件的航空器数目表示为D2(i)；定义D3(i)为D1(i)、D2(i)航空器数量的集合。

对于进场运动的航空器，针对于离场航空器i，如果航空器j在航空器i撤轮挡前已经落地且航空器j上轮挡时间在航空器i撤轮挡时间之后，那么航空器j属于对航空器i滑行时间有影响的场面进场运动航空器，所有满足此条件的航空器数目表示为A1(i)；针对于离场航空器i，如果航空器j在航空器i撤轮挡后落地且航空器j落地时间在航空器i离场时间之前，那么航空器j属于对航空器i滑行时间有影响的场面进场运动航空器，所有满足此条件的航空器数目表示为A2(i)；定义A3(i)为A1(i)、A2(i)定义航空器数量的集合；针对于离场航空器i，如果航空器j在航空器i撤轮挡后落地且在航空器i起飞前上轮挡的，那么航空器j属于对航空器i滑行时间有影响的场面进场运动航空器，所有满足此条件的航空器数目表示为A4(i)。

笔者对上述定义解释度进行对比分析，得出拟合程度最高的定义结果。

表3 进、离场滑行航空器定义R2值

通过对表3的结果研究，笔者选取定义D2(i)(离场)与定义A2(i)(进场)作为模型输入变量。

1.2.4 跑道运行模式

跑道运行模式的改变分为跑道运行方向改变和多跑道组合起降方式的改变。不同跑道运行模式下，其进离场航空器交通流相互作用的范围不同，造成航空器滑行时间的差异。跑道运行模式通常以“A1，A2 |D1，D2”的形式来描述，其中A1和A2是降落跑道，D1和D2为起飞跑道。例如“36R,01|36L,36R”代表机场在该时段下跑道36R，01跑道作为降落跑道，而36L，36R跑道作为起飞跑道。理论上，若该机场有n条跑道，每条跑道两个方向，其跑道运行模式会有6n种可能，因为每条跑道分为进场、离场、或进离场混合运行3种模式。但在实际运行中，由于机场盛行风向及交通流量变化的原因，机场通常使用3～5种跑道运行模式，不同跑道运行模式下的航空器滑行时间不同。笔者运用哑变量对跑道运行模式进行描述，若该航空器使用此跑道运行模式，则设为1，否则为0。首都机场不同跑道运行模式使用的频率见表4。

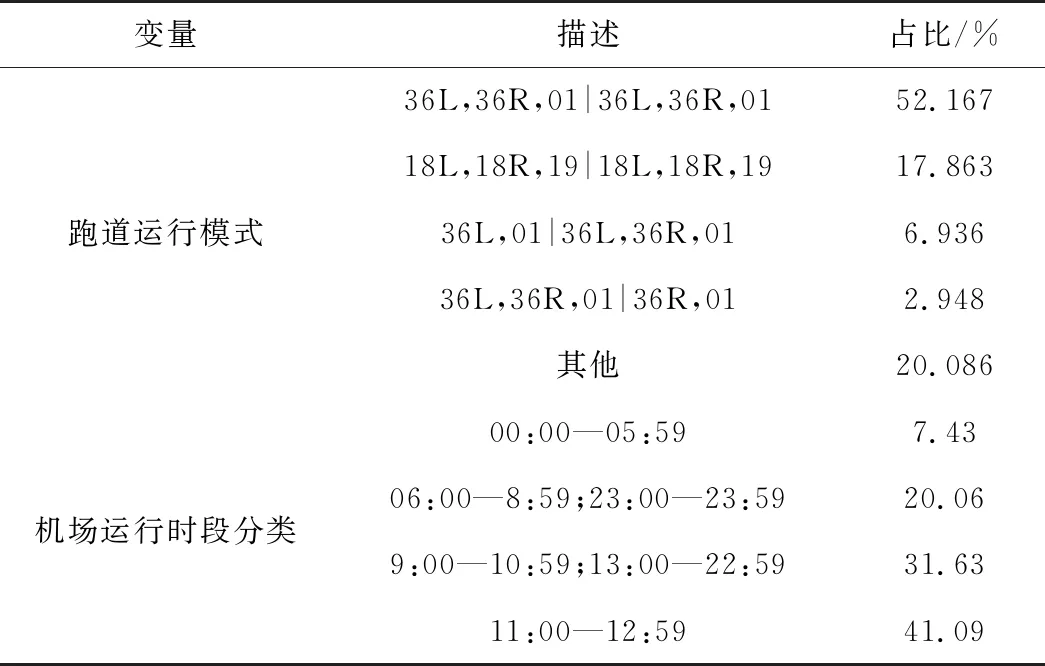
表4 跑道运行模式及运行时段使用频率

1.2.5 机场运行时段分类

在不同时间段下，机场流量也各不相同，从而导致滑行时间的差异。高峰时段的进离场航空器数量多，机场场面运行负荷大，航空器滑行时间要大于非高峰运行时段。为提高预测准确度，对首都机场的进离场航空器数量进行分段分析，运用DBSCAN聚类算法按照每小时场面运动的航空器数量为依据进行划分，若航空器在场面上为跨小时运行的，则这两个时段都将该航空器计入统计。 DBSCAN算法结果显示，按照机场每小时进离场航空器数量将24 h划分为4类，如表5。

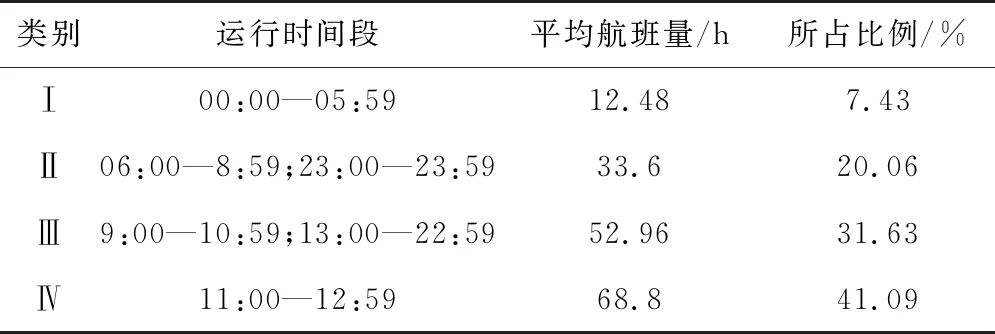
表5 基于DBSCAN算法的运行时间段分类

通过DBSCAN算法结果可知，00：00—05:59时间段平均每小时航班数量约为12架次。06:00—8:59、23:00—23：59两个时间段由于其每小时的场面航空器数量平均为33.6架次，所以被整合为同一个时间分类。9:00—10:59、13:00—22：59两个时间段内其每小时场面航空器数量平均为52.96架次，所以将这两个时间段划分为一个时间段。最后将11：00—12:59划分为一个时间段，这个时间段内，平均每小时场面航空器数量达到最多，为68.8架次。

滑行时间预测模型中所有变量统计分析信息见表4和表6。

表6 首都机场滑行时间预测模型变量统计分析信息

2 离场滑行时间预测与分析

对滑行距离(x1)、进场航空器数量(x2)、离场航空器数量(x3)、跑道运行模式(x4)4个变量建立多元线性回归模型及机器学习模型，分别对不同时间分类下航空器滑行时间进行建模。

2.1 机器学习滑行时间预测分析

机器学习中多元线性回归模型与传统统计学多元线性回归模型的区别在于统计学方法得出的结果是最小化数据点之间的平方误差，无区分训练集与测试集，主要评估变量与结果之间的重要性与稳健性。而机器学习是将数据随机区分为训练集与测试集，在训练集上对数据进行拟合，将所得的结果在测试集中进行测试，找出误差较大的数据，并利用损失函数对模型不断进行修正与测试，最终得出较为精准的预测模型。

Lasso回归在线性回归优化函数的基础上增加了L1范数正则项以防止模型出现多重共线性及过拟合情况。其优化函数如式(5)：

(5)

笔者以11:00—13:00时段为例，对该时段影响离场航空器滑行时间做逐步多元回归拟合，得出的结果如表7及图2。

表7 11:00—13:00时段机器学习回归模型预测评价指标

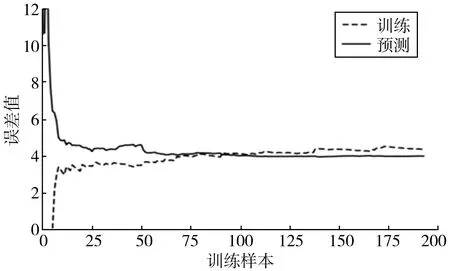
图2 11:00—13:00预测模型学习曲线

表8为在机器学习预测模型中加入DBSCAN算法对运行时段分类后，不同时间分类下的机器学习Lasso回归模型预测结果评价。

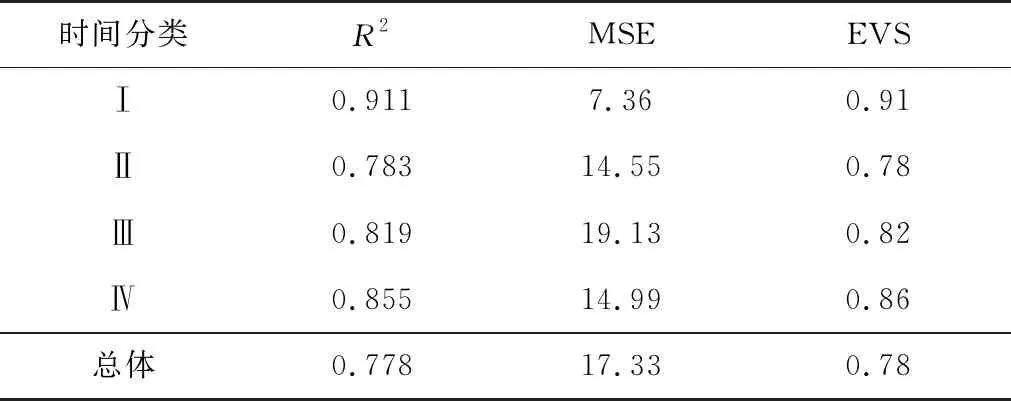
表8 基于机器学习模型预测评价指标

从表8中可知，在进行不同时间段分类后的模型拟合效果均优于未进行分类的模型总体拟合效果，表明运用DBSCAN算法进行机场运行时间分类可进一步提高模型的准确率。

机器学习Lasso回归中有两个参数需要进行调整，一个是训练集与数据集的比例，另一个是随机种子的选取。这两个参数共同作用于模型的稳健性与可预测性，通过对数据集按不同比例的划分，其最终模型的R2与MSE也不相同。一个好的模型需要高R2值与低MSE值，所以笔者将以R2与MSE的差来计算：

P=R2-MSE

(6)

式中：R2与MSE均已进行无量纲化处理，得到结果如图3。

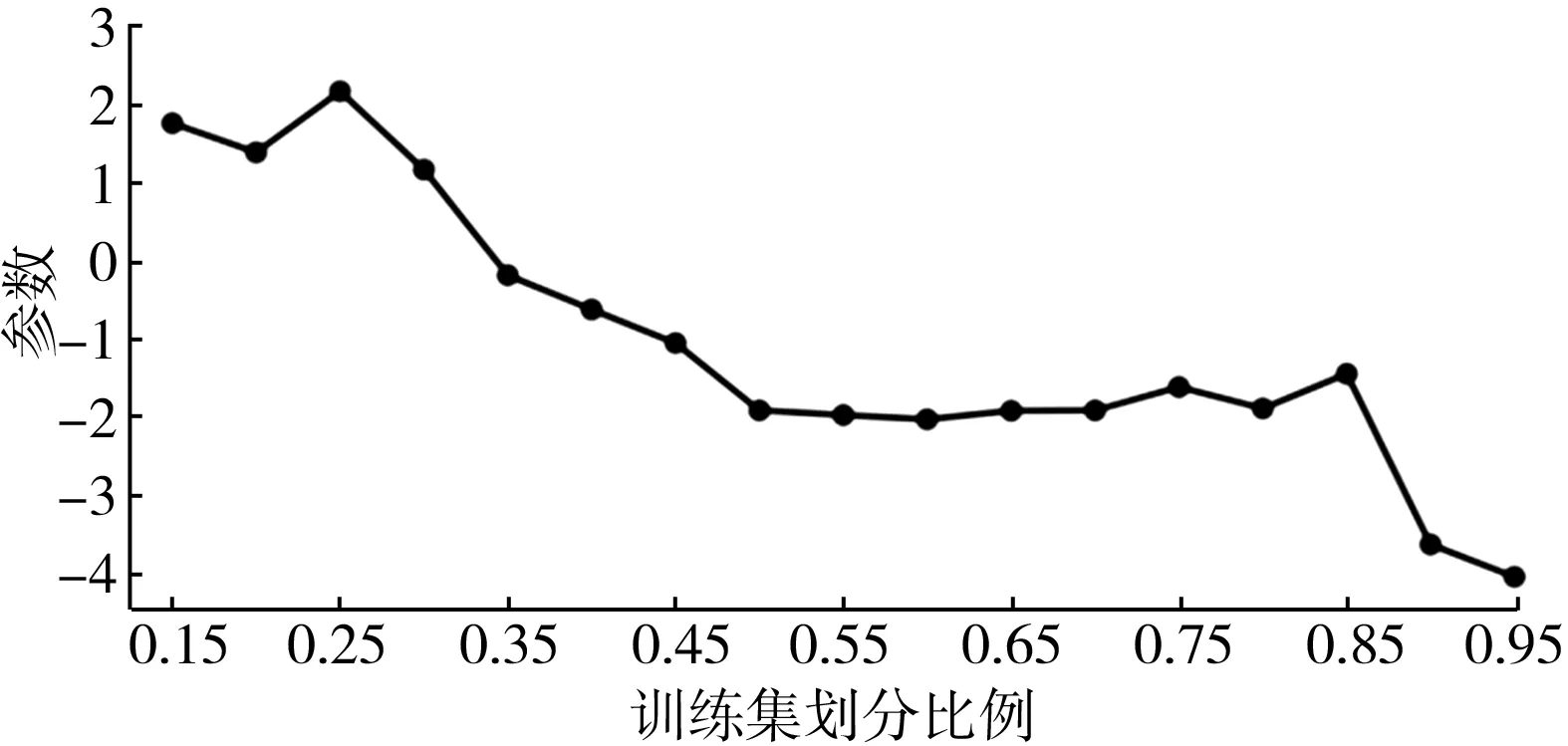
图3 Lasso回归调参图

由图3可知，在预测集与训练集为0.75∶0.25的比例分开，且随机种子选取为0时，模型拟合效果最好。

2.2 基于传统统计学的预测模型

基于传统统计学的回归模型[式(7)]对滑行距离(x1)、进场航空器数量(x2)、离场航空器数量(x3)、跑道运行模式(x4)4个变量建立多元线性回归模型：

Y=βixi+ε(i=1,2,…,n)

(7)

利用SPSS进行运算，模型全部通过了T检验及显著性检验。笔者以I类系数分析为例进行展示，结果如表9。

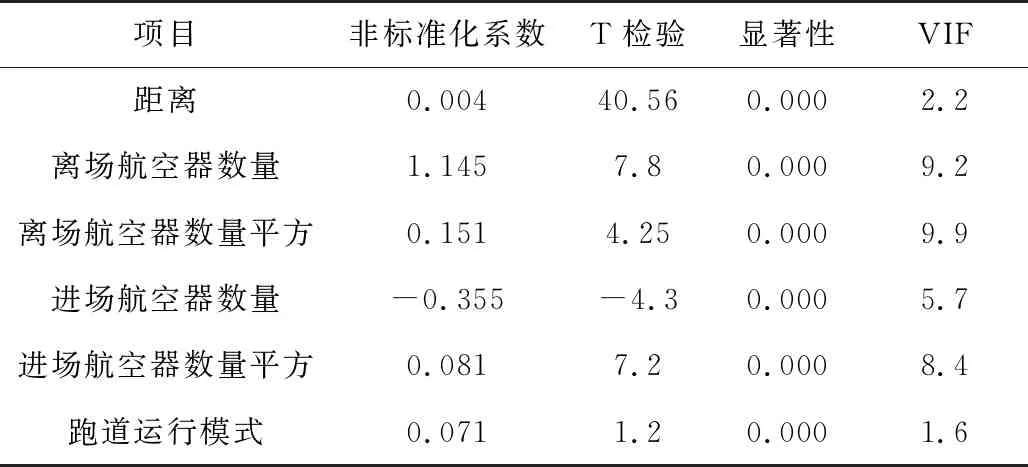
表9 Ⅰ类系数分析

2.3 模型准确度对比评价

预测值与实际值的误差如图4。共提取100个预测值与实际值数据进行绘图。由图4可以看出，预测值与实际值的大致走向趋于一致，说明模型的拟合程度较好。通过对结果的比较来看，机器学习方法对首都机场全天离场滑行预测结果与实际结果在±3 min的准确性平均达到69.3%，±5 min的准确性达到87%。

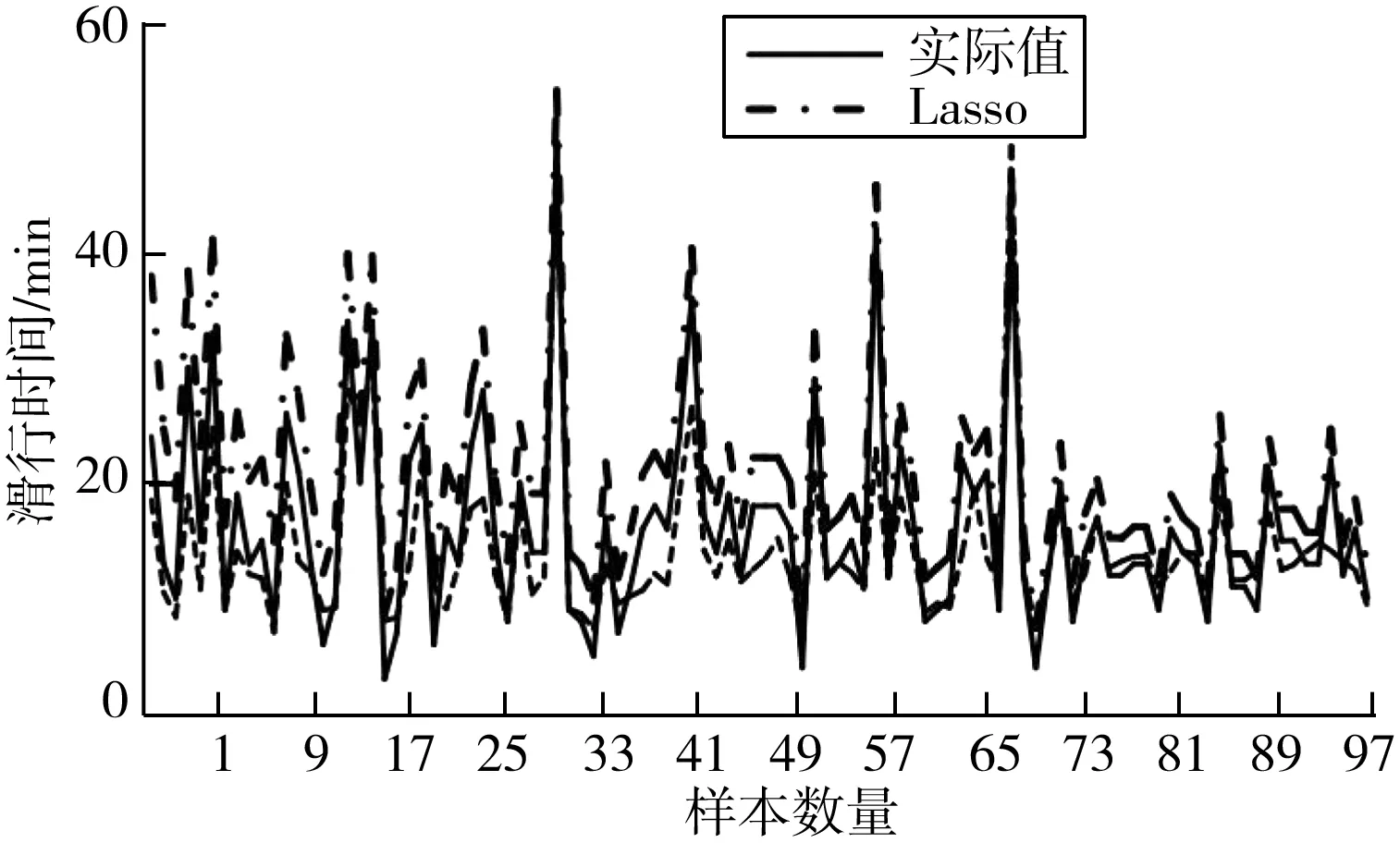
图4 机器学习与统计学预测准确率对比

笔者以误差图与±1、±3、±5 min准确率对比这3个指标对模型的准确性进行评价。准确率为模型预测时间与实际滑行时间的差值在某一设定范围内的数量与总预测样本数之比。例如±3 min准确率为实际值与模型预测值相差3 min以内的样本数量占所有预测样本数的百分比。离场滑行时间预测值与准确值误差如表10。

表10 模型预测准确率对比

同时，将笔者的模型结果与现有其他学者的研究成果进行对比发现，在运用DBSCAN算法进行机场运行时段分类后的模型拟合效果(R2=0.78)高于未进行运行时段分类的模型[11](R2=0.70)，也高于使用计量经济学回归方法[8]的效果(R2=0.74)。由此表明，在利用DBSCAN算法及引用跑道运行模式的航空器滑行时间预测模型拟合效果更好。

3 结 论

对首都机场航班运行数据进行分析，最终得出影响滑行时间的因素为滑行距离、进场航空器数量、离场航空器数量、跑道运行模式和时间段。

通过分析发现：

1)滑行距离与进、离场航空器数量这3个变量对模型的预测贡献程度较大。

2)跑道运行模式的变化会引起滑行时间的波动，所以跑道运行模式这一变量的引用可以进一步提高预测的精确度。

3)不同时间段内的航班数量不同。为提升模型的准确性，笔者运用DBSCAN算法按每小时航班流量对机场运行时段进行分类建模。

4)运用机器学习与传统统计学两种方法建立多元回归模型对离场滑行时间进行预测。结果显示，机器学习交叉训练集下多元回归模型的预测准确度较高，预测与实际误差值在5 min内的占87%，可用于大型机场实际运行航班滑行时间预测。