结合Kriging与改进NSGA-II的RV减速器优化

缪嘉成，李朝阳，陈兵奎

(重庆大学 机械机械传动国家重点实验室，重庆 400044)

RV(rotational vector)减速器是一种效率高、体积小、重量轻、扭转刚度大、传动精度高的新型传动机构，在工业机器人、数控机床、医药化工设备等领域应用广泛。其设计参数众多，约束条件复杂，传动性能相互耦合，传统设计方法难以获得最优解。随着优化理论逐渐成熟，多目标优化算法逐渐应用于摆线类减速器设计。Wang等[1]对K-H-V摆线减速器进行了优化，提升了传动效率并缩小了体积。Wang等[2]改进了NSGA-II算法，增强了种群的分布性，并用于摆线针轮减速器的优化。Jat等[3]使用NSGA-II对深沟球轴承的基本额定动载荷和弹流动态最小膜厚度进行了优化。

扭转刚度是RV减速器的关键性能指标之一[4]。中外学者针对摆线及RV减速器刚度特性进行了深入研究[4-7]，但未见针对其刚度优化方法的报道。RV减速器刚度分析通常采用数值方法或ANSYS有限元仿真[4,6]，前者难以精确反映减速器结构参数与扭转刚度间的非线性关系，后者的计算量难以满足优化算法的要求。为减少耗时的CAE(computer aided engineering)模拟，需结合理论模型与CAD (computer aided design)二次开发，建立部分扭转刚度的Kriging代理模型[8]。

RV减速器结构优化的关键是解决多目标混合整数非线性规划(MOMINLP, multi-objectives mixed integer non-liner programming)问题，求解小样本问题常用分支界定法、割平面法等精确算法。由于精确方法求解高维问题的时间复杂度极高，中外学者对进化算法加以改进[9]，部分研究基于实数编码的粒子群算法(PSO, particle swarm optimization)或差分进化算法(DE, differential evolution algorithm )，利用三角函数、Sigmod函数等建立实数与整数的映射关系[10-11]。

笔者以BAJ-25E为研究对象，建立RV减速器效率和体积的目标函数以及部分刚度的Kriging代理模型，提出一种能够同时处理离散种群、整数种群与实数种群的改进NSGA-II算法，并将其应用于RV减速器的结构参数优化。

1 结构优化的数学模型

RV减速器的结构如图1所示，为保证与现有RV减速器的兼容性，基本参数由设计人员给出，包括输入功率P(W)、输入转速n(r/min)、行星轮个数np、输出扭矩T2(mN·m)，表示为

图1 RV减速器结构原理图Fig.1 Structure of the RV reducer

(1)

(2)

1.1 RV减速器的性能指标

由于RV减速器的体积与扭转刚度的耦合关系较强，需同时考虑体积和扭转刚度目标，传动效率作为重要性能指标也应纳入优化目标。

1.1.1 体积

在满足RV减速器所需的输入功率和输出转矩的基础上，将减小外形尺寸作为设计目标。如图2所示，体积目标函数为

图2 一体化RV减速器外形尺寸Fig.2 Dimensions of the integrated RV reducer

[(d3+2(τ1+τ2+τ3))2-(d3+2τ1)2]h3},

(3)

式中：τ1,τ2,τ3表示针齿壳各部分的厚度；h1,h2,h3表示针齿壳各部分的长度，h3=δ1+b+δ2+2L′+2B-h1-h2，d3=d1+2d2。δ1和δ2分别表示输出端盘端面到行星轮端面的距离，以及行星轮端面到支承轴承端面的距离。

1.1.2 扭转刚度

影响RV减速器刚度的元件主要有输入轴、渐开线行星传动机构、转臂轴承、支承轴承、曲柄轴和摆线针轮传动机构。

1)在输入扭矩T1作用下，输入轴的扭转角为

式中di为输入轴各部分的直径。

2)通过数值弹性力学求解，渐开线行星传动机构总啮合刚度为

cr=(0.75εα+0.25)c′，

(4)

式中：εα为端面重合度；c′为单对齿刚度。

3)转臂轴承为一体化滚子轴承，以圆柱滚子为滚动体，曲柄轴为内滚道，摆线轮坐标孔为外滚道，材料为GCr15。采用单列短圆柱滚子轴承刚度经验公式[12]计算转臂轴承的径向刚度为

(5)

4)支承轴承同为一体化滚子轴承，考虑变形协调条件，输出端盘刚性较大，视为刚体。np对支承轴承在输出端盘扭矩的作用下将产生相等的径向形变，单个支撑轴承的径向力为

(6)

式中asp为渐开线齿轮中心距。将|R′|代入式(5)，可得支承轴承径向刚度K′r。

5)根据文献[14]，曲柄轴的总变形为

(7)

式中：Li为曲柄轴各段的长度；I为惯性矩；E为弹性模量;Ft为切向分力。

6)由文献[4]可知，摆线针轮传动处于低速级，对减速器扭转刚度的影响较大，故采用CAE仿真计算摆线轮与针齿间啮合刚度K″，以提高模型的精度。为提高CAE模型建模效率，开发了参数化建模软件，图3为典型零件图形化建模界面。

图3 RV减速器参数化建模软件Fig.3 Parametric modeling software of the RV reducer

用户界面采用三维建模软件NX12的Block UI Styler实现，通过C++完成用户界面编辑及尺寸参数定义，采用Visual Studio对程序进行编译与链接。尺寸驱动的RV减速器模型将创建三维模型的过程分解，分别对特征、对象、实体的操作进行函数化处理。在建模界面输入Kriging样本点对应的尺寸参数，驱动软件生成三维零件图。

将图3所示摆线针轮传动模型导入仿真软件中，对针齿壳施加固定约束，在摆线轮端面施加额定扭矩Tg，其中单个摆线轮传递的扭矩Tg=0.55T2。对摆线轮和针齿壳进行自动网格划分，对涉及接触作用的区域局部细分，采用Abaqus二次开发实现上述流程的自动化，如图4所示。通过脚本接口建立图形用户界面GUI与内核的通信，提取摆线轮在扭矩Tg作用下当前角度的角位移βH。

图4 摆线针轮有限元分析程序Fig.4 FEM analysis program of the cycloid-pin

将输入轴与针齿壳固定，在输出轴上施加额定扭矩T2，各弹性元件将引起相应的弹性转角θi如表1所示，RV减速器的总刚度K′[7]为

表1 各元件引起的弹性转角Table 1 Elastic angle caused by each component

(8)

1.1.3 传动效率

RV减速器的主要效率损失来自于齿轮啮合摩擦损失和轴承摩擦损失[15]，表示为

η=η16ηB。

(9)

式中：ηB为轴承总效率，η16为封闭差动齿轮传动效率，

1.2 结构参数的约束条件

1)考虑相邻行星轮齿顶不干涉(g4)、行星齿轮装配条件(h1)、弯曲接触强度(g5,g6)等，如表2所示。

表2 渐开线行星传动机构的约束条件Table 2 Constraints of the involute planetary transmission

2)考虑圆柱滚子安全接触应力(g8)[3]、转臂轴承几何约束(g10)、轴承寿命(g11)等，如表3所示。

表3 转臂轴承的约束条件Table 3 Constraints of turning arm bearing

表中的Qmax=4.08×10-3|R|/Z；s为安全系数；[σc]为许用压应力；Do为行星轮传动轴直径；e为偏心距；nb为转臂轴承内外圈相对转速；寿命指数ε=10/3；p为平均当量动载荷；基本额定动载荷Cd为

平均当量动载荷p为

支承轴承的约束条件相似，故不再赘述。

3)考虑针齿分布圆直径(g12)、摆线轮不根切条件(g16)、摆线针轮接触强度(g17)等，如表4所示。

表4 摆线针轮传动机构的约束条件Table 4 Constraints of the cycloidal pin transmission

4)考虑两级传动的尺寸均衡(g18)，并保证最大输出转矩(g19)，如表5所示。

表5 整体约束条件Table 5 Overall constraints

2 多目标优化的理论基础

2.1 MP-NSGA-II算法

ridPSO和ridDE[10-11]是适用于单目标MINLP问题的主流算法，不具备多目标寻优能力。笔者结合多目标进化算法NSGA-II提出MP-NSGA-II。该算法继承了NSGA-II解集分布性良好、时间复杂度低、收敛速度快等优点,并且扩展了处理实数、整数及离散变量的能力。

图5 MP-NSGA-II算法流程图Fig.5 MP-NSGA-II algorithm flow chart

处理混合种群的具体步骤为：

1)产生初始种群：利用设计变量的取值范围生成自变量范围矩阵，根据前m1个连续变量和后m2个离散变量在矩阵中的位置将其分割为2个子矩阵Mr和Mi。针对子矩阵Mr，使用rand函数生成一个实数值的初始种群Pr。针对子矩阵Mi，使用rand函数和四舍五入法生成一个十进制整数的初始种群Pi。

2)混合种群交叉：种群Pr和Pi均是行数为种群规模，列数为设计变量数的矩阵，将Pi转化为浮点数矩阵，两矩阵水平合并，生成混合种群Pm,采用两点交叉实现个体间染色体的重组。

3)子种群变异：将混合种群分割为子种群Pr和Pi，Pi转化为整数矩阵。采用实数值高斯变异算子对Pr进行变异，整数值变异算子实现矩阵Pi中个体突变，并将两矩阵合成混合种群Pm。

由于截断法[9]只能处理连续的整数变量，为处理MIP(mixed integer programming)问题中的离散变量，提出一种基于数组索引的离散变量通用编码方案如图6。将离散变量Zd的nd个可取值设为数组Zarr,数组索引编码为取值(0,1,…,nd-1)的整数子种群Znum。在评估函数值和限制条件的阶段，根据数组Zarr和数组索引种群Znum解码出离散子种群Zdis。

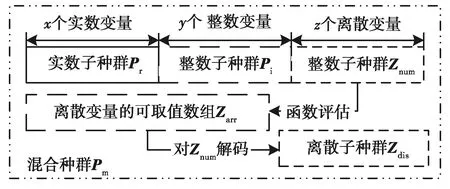
图6 离散变量通用编码方案Fig.6 Discrete variable universal coding scheme

为增强种群的分布性并降低计算代价，引入考虑拥挤距离的非支配排序。由于计算欧氏距离的效率较低，采用差分计算目标值的偏移量占比代表拥挤距离。根据混合种群个体目标值由小到大排序，两相邻个体xi和xj间的拥挤距离定义为

(10)

式中：f(x)是个体x的目标值，f(x)max和f(x)min分别是混合种群中最大和最小的目标值。根据拥挤距离更新个体的适应度Vfit，用于选择下一代个体。

2.2 双加点准则Kriging代理

利用拉丁超立方试验设计在设计变量空间内采样，得到Kriging代理模型的初始样本点，样本点满足使下式取得最小值：

(11)

Kriging代理模型定义了设计变量x与预测值y的关系，表达式[8]为

y(x)=F(β,x)+z(x)，

(12)

式中：F(β,x)为设计变量空间的全局模型，z(x)为按N(0,σ2)随机分布的局部偏差,z(x)的统计特征为

(13)

R(xi,xj)是用于刻画样本点xi和xj间关联程度的相关模型，通常采用高斯相关模型

(14)

利用线性加权插值方法得到Kriging模型在预测点x处的响应值和预测方差：

(15)

(16)

式中：R是相关模型矩阵；r(x)是x点与样本点间的相关模型向量；g是样本点响应的向量；q是元素均为1且个数为nv的单位列向量。

在优化过程中添加样本点可有效提高代理模型的精度，通常选择在期望提高(EI)或均方误差(MSE)较大处加点。为有效利用进化算法优化过程中的信息，将Pareto最优集引入加点准则。在迭代过程中根据Pareto集的拥挤距离选择分散样本点更新Kriging模型。单次迭代中均方误差较大处加点数SE和Pareto最优解处加点数SP分别为

(17)

式中：g是迭代总次数；gc是当前迭代数；CE和CT分别是调整系数和最小加点数。

2.3 熵权法Pareto选优

熵权法是一种客观赋权方法，利用决策指标的熵计算熵权值，在i个性能指标X1,X2,…,Xi，j个Pareto最优解的评价问题中，第p个性能指标Xp={x1,x2,…,xj}，Xp的熵Hp定义为

(18)

(19)

3 优化方法的验证及实现

3.1 MP-NSGA-II评估

为评估MP-NSGA-II算法的有效性，对文献[11]中的14个MINLP问题进行仿真，已知最优源自MDE、MDELS、MDEIHS、ridPSO和ridDE。

表6均为最小化目标问题，MP-NSGA-II的种群规模为1 000。为体现算法的收敛特性，进化代数设为10 000。MP-NSGA-II单次运行最优解与已知最优差距小于0.1%，并改进了3个已知最优解：P5(x=1.374 823 1,y=1)，P9(x=[27,27,27],y=[88,44])，P12(x=[0.902 19,0.887 75,0.949 18, 0.848 72],y=[5,5,4,6])。由于P7中已知最优的自变量x2=0时目标函数分母为0，原解不成立。

表6 MINLP基准问题仿真Table 6 MINLP benchmark simulation

3.2 Kriging近似模型

图7 Kriging可视化模型Fig.7 Kriging visual model

采用复相关系数R2检验拟合模型的精度为

(20)

复相关系数越接近1，近似模型的精度越高。选择16个样本点检验Kriging模型的精度，如图8所示。检验得复相关系数R2为0.920 8，说明该代理模型的精度能够满足结构优化的需要。

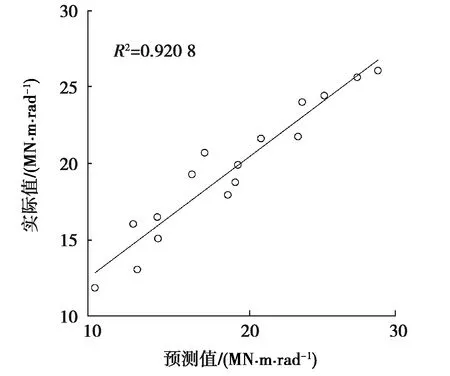
图8 Kriging模型精度检验Fig.8 Precision validation of the Kriging model

3.3 结构优化子程序

RV减速器的优化目标为{η,V,K′}T，约束函数为几何及应力约束，优化模型为

(21)

式中：g(X,C)为不等式约束；h(X,C)为等式约束。

由上述的优化模型及算法原理，以PySide2为开发框架，编写一体化结构RV减速器设计软件。其优化子程序如图9所示，由基本参数及设计变量设置、优化算法参数设置及优化结果输出组成。

根据RV减速器的实际工况给出RV减速器的动力学及结构基本参数，如图9左上。根据RV减速器的设计要求及BAJ-25E减速器的设计参数，初算设计变量范围，如图9左下。

图9 一体化结构RV减速器设计软件界面Fig.9 Integrated RV reducer design software interface

设置MP-NSGA-II算法的种群规模为3 000，遗传代数为1 000，代沟为0.5，交叉概率为90%，变异概率为10%。选择方式为轮盘赌选择，重组方式为两点交叉。Pareto前沿如图10所示，可知优化目标间相互制约，需从解集中优选理想解。

图10 Pareto前沿Fig.10 Pareto frontier

生成RV减速器的结构及性能参数表如图9右下所示。设定传动效率及扭转刚度下限和体积上限，以缩减Pareto最优解集的规模。

4 结果与分析

各优化目标通过结构参数相互耦合，利用两目标的Pareto前沿分析优化目标间的耦合关系，为后续的Pareto选优提供依据，如图11所示。

图11 各优化目标间的耦合关系Fig.11 Coupling relationships between optimization objectives

从图11(a)和(b)可看出扭转刚度和体积变化时，传动效率维持在85.2%～85.6%，与其余优化目标的耦合关系不显著。11(c)表明体积与扭转刚度成显著正相关。因此，主要考虑体积和扭转刚度的设计要求，初步筛选5个设计方案如表7所示。

表7 初选设计方案Table 7 Preliminary design selection

采用熵权法，将性能指标决策矩阵归一化，求解各指标的信息熵Hp，并计算各目标熵权值：

wp=[0.293 2,0.318 6,0.388 2],p=1,2,3。

由熵权值wp及归一化指标rpq对各方案评分，为

Zq=r1qw1-r2qw2+r3qw3(q=1,2,3,4,5)。

(22)

根据Zq排序，选择理想方案2。BAJ-25E的结构参数与优化后的RV减速器参数如表8所示。

表8 优化参数对比及敏感性分析Table 8 Comparison of optimized parameters and sensitivity analysis

由表8知，经MP-NSGA-II算法优化可直接获得符合约束条件的优化值，无需圆整处理。与初始值相比，优化解的传动效率提升了1.24%，体积减小了1.69%，扭转刚度增大了53.83%。

在制造过程中，尺寸参数可能出现1%左右的偏差[3]，对性能指标的敏感性分析有助于指导实际生产中的误差控制。研究连续变量变化±1%对优化后的减速器扭转刚度的影响，如表8。可见Dz、K1、L和L′对扭转刚度的影响均超过0.5%，其它参数波动的影响较小，均低于0.2%。

5 结 论

1)分析了影响RV减速器性能的结构参数，综合17个设计变量，3个目标函数和21个约束条件建立了结构优化的数学模型。

2)提出MP-NSGA-II算法，利用MINLP基准问题测试了改进算法的性能，并改进了3个已知最优解，证明了该算法的有效性。

3)结合Kriging与MP-NSGA-II得到Pareto前沿，利用熵权法完成Pareto选优，有效提高了RV减速器的综合性能。