应用于汽车发动机start/stop模式的磁流变悬置设计与分析

邓召学，杨青桦，蔡 强，刘天琴

(重庆交通大学 机电与车辆工程学院，重庆 400074)

汽车的振动特性对乘客乘坐的舒适性有很大影响。车辆振动的特点是振源多，形态复杂[1]。振动主要来自于发动机，通过发动机悬置传递到车身。考虑到目前车辆大量集中在城市里，因此主要运行工况为城市工况，城市工况要求汽车频繁地启动(start)、关闭(stop)发动机，此时发动机产生大的位移和扭矩激励传递到悬置。为了减少start/stop模式下的车辆振动，所安装的发动机悬置应该具有高阻尼和大刚度[2]。

磁流变液(MRF)作为一种新型智能材料，具有可控性好、响应迅速、能耗低等特点[3]。因此应用于汽车发动机液压悬置系统时，通过控制其磁场可以表现出很好的隔振性能[4-8]，实现真正意义上的宽频隔振[9-10]。

Yang等[11]设计了一种带复位弹簧的周径向流动式磁流变悬置，试验表明该结构可以改善磁流变悬置在低频和高频段的隔振性能。Nguyen等[12-13]设计了一种新型的可用于船舶等中高速发动机的流动和剪切混合工作模式的磁流变悬置，与传统磁流变悬置相比可实现多向隔振。Kang等[14]提出了一种应用于中高速柴油发动机的磁流变悬置，实验结果表明该悬置至少有10 kN的阻尼力，当激励电流达到3 A时，磁流变悬置可减少50%的振动激励。Yoon等[15]设计了一种用于重型货车的半主动磁流变悬置，通过仿真计算了该悬置的阻尼力和可控范围，证实该悬置可以有效地隔离振动传递。吴群等[16]为提高发动机低频段的隔振性能，研究了磁流变悬置参数对低频动特性的影响。目前人们对磁流变悬置的阻尼力数学模型进行了大量的研究分析[17-19]，但是很少涉及液阻效应和电流对磁流变液黏度的影响规律。

针对汽车发动机在start/stop模式下产生大位移和大扭矩的特点，设计了一种具有惯性通道的流动模式磁流变悬置，考虑激励电流对磁流变液黏度的影响规律和磁流变悬置的液阻效应，建立了悬置的阻尼力数学模型。通过理论分析、仿真计算和试验验证，对磁流变悬置的隔振性能进行了研究。

1 磁流变悬置结构

所设计的流动模式磁流变悬置结构如图1所示。磁流变悬置主要由用于承载静载荷的橡胶主簧、螺栓杆、悬置壳体和橡胶底膜、扰流盘和惯性通道以及设置在橡胶底膜上方将隔振腔分为上液腔和下液腔的磁芯组件构成，隔振腔内充满磁流变液。磁芯组件由励磁线圈、内磁芯、外磁芯、隔磁套筒、上隔磁板和下隔磁板组成，内磁芯和外磁芯之间的环形通道构成阻尼通道，外磁芯和壳体上设有横向导线孔。励磁线圈在施加电流时产生的磁通穿过内磁芯、阻尼通道和外磁芯构成磁回路。

所设计的流动模式磁流变悬置具有输出阻尼力大、可靠性高、结构简单等优点。通过改变激励线圈电流大小来控制流动阻尼通道处的磁场强度，进而改变其输出阻尼力，实现对发动机振动的有效衰减，缓解汽车发动机在启动、熄火等低频条件下的大位移振动。

1.橡胶底膜；2.下隔磁板；3.阻尼通道；4.励磁线圈；5.上隔磁板；6.橡胶主簧；7.螺栓杆；8.扰流盘；9.隔磁套筒； 10.内磁芯；11.导线密封螺栓；12.外磁芯；13.惯性通道图1 磁流变悬置结构示意图Fig.1 Structure of the MR mount

2 阻尼力数学模型

由图2可知，磁路结构中的阻尼通道是磁流变悬置的核心。阻尼通道的进出口压降决定了悬置的隔振性能，而磁路结构、激励电流等因素决定了阻尼通道处的磁感应强度，进而影响阻尼通道内的液阻大小，使得阻尼通道进出口压降发生变化。

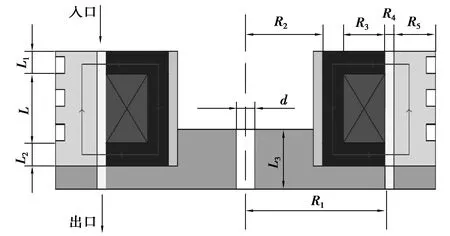
图2 磁流变悬置磁路结构示意图Fig.2 Structure of the MR mount magnetic circuit

为了便于分析所提出的悬置模型，对模型进行以下假设简化：1)磁流变液为不可压缩流体；2)磁流变液在阻尼通道内的流动为层流状态；3)悬置仅受垂直方向上的正弦振动激励。

在垂直激励下，悬置橡胶主簧产生位移，迫使磁流变液从上液腔通过阻尼通道和惯性通道流向下液腔的液体流量Qi为

(1)

阻尼通道液阻Ri1为

(2)

惯性通道液阻Ri2为

(3)

流经阻尼通道的流量Q1可表示为

(4)

阻尼通道内压降为

(5)

惯性通道内压降为

(6)

式中：η1为有效阻尼通道处磁流变液的黏度，该黏度与激励电流呈非线性关系；η0为磁流变液的零场黏度；Lz为流动阻尼通道总长度，Lz=L1+L2+L；L1、L2分别为单侧有效阻尼通道长度，L1=L2；L为无效阻尼通道长度；d1为流动阻尼通道的等效直径，d1=2R1+R4；R1为内磁芯半径；R4为阻尼通道间隙宽度；L3为惯性通道的长度；d为惯性通道直径；ΔPη为由磁流变液流动时自身黏性引起的压力差；ΔPMR为在磁场作用下磁流变液流动时受到剪切屈服应力引起的压差；CA为修正系数，取值范围为2～3；τBY为磁流变液的剪切屈服应力。

磁流变悬置的输出阻尼力可表示为

(7)

由式(7)可知，第1部分是由液体自身黏度产生的黏性阻尼力，第2部分是与磁场相关的可控阻尼力，第3部分为液体通过惯性通道引起的阻尼力；通过控制励磁线圈电流的大小可实现对悬置输出阻尼力的连续调控。

悬置的恢复力F可表示为

(8)

式中：Fe为橡胶的主簧力，λ为橡胶主簧的动态硬化系数，k为橡胶主簧静刚度，X为正弦激励的幅值。

3 磁流变悬置仿真分析

3.1 磁场仿真分析

磁流变悬置的可控性能取决于悬置的磁路结构，使用ANSYS电磁仿真模块对悬置内部磁场进行了仿真分析。悬置的磁路结构截面具有对称性，因此在不影响仿真结果的条件下，采用简化后的2D轴对称四节点四边形单元(PLANE13)模型进行有限元分析；为防止漏磁，隔磁组件采用低磁导率的铝制材料；内、外磁芯由电工纯铁(#DT4)制成，仿真计算时假设该模型边界无漏磁。经过多次仿真计算，得到磁路结构的主要参数如表1所示。

表1 磁流变悬置磁路结构参数Table 1 Structural parameters of the MR mount magnetic circuit

悬置使用的磁流变液为重庆仪表材料研究所生产的MRF-250型磁流变液，该磁流变液零场黏度为0.25 Pa·s，密度为2.65 g/mL。其黏度η1和剪切屈服应力τy受激励电流产生的磁场影响。根据所提供的屈服应力数据，采用多项式曲线拟合方法得到磁流变液黏度η1与激励电流I、屈服应力τy与磁感应强度B的关系如图3～4所示。

图3 磁流变液η1-I曲线Fig.3 The η1-I curve of the MRF

图4 磁流变液 τy-B曲线Fig.4 The τy-B curve of the MRF

磁流变液黏度与电流的拟合多项式为

η1=0.282 9-10.451I+119.26I2-143.91I3+88.826I4-29.132I5+3.928 2I6。

(9)

剪切屈服应力与磁感应强度的拟合多项式为

τy/kPa=0.0387 2+9.511 2-4B+9.138 2-7B2-1.195 0-10B3+3.076 9-14B4-

3.782 3-18B5+1.417 7-22B6。

(10)

图5为给励磁线圈施加1.0 A电流、阻尼通道间隙为2 mm时的磁路结构有限元分析结果。

图5(a)为悬置磁路的磁感应强度分布图，从图中可以看出，磁路的磁感应强度分布比较均匀；上、下有效阻尼通道处的磁感应强度远大于中部无效阻尼通道处的磁感应强度，并且中部无效阻尼通道处的磁感应强度趋于0，说明励磁线圈产生的磁通主要穿过磁芯，符合设计要求。图5(b)为磁路的磁通分布图，可以看出大部分磁通主要沿磁通路径分布，并且垂直穿过有效阻尼通道；因为DT4的导磁性能优于磁流变液，导致了小部分磁通未垂直穿过阻尼通道。

图5 电流为1.0 A、阻尼通道间隙为2.0 mm时磁路的仿真结果Fig.5 The simulation results of the magnetic circuit when the current is 1.0 A and the damping gap is 2.0 mm

对阻尼通道内等比取2列各40个节点进行编号，如图6所示，提取节点处的磁感应强度，并且将2列节点处的磁感应强度一一对应求平均值，得到如图7所示的不同阻尼通道宽度下的磁感应强度曲线。由曲线可以看出，有效阻尼通道处的磁感应强度分布相对均匀,当阻尼通道间隙为2 mm时有效阻尼通道处的平均磁感应强度为0.437 T，阻尼通道间隙为1 mm时有效阻尼通道处的平均磁感应强度为0.644 T。随着阻尼通道间隙宽度逐渐减小，有效阻尼通道处的磁感应强度逐渐增大。

图6 阻尼通道节点编号Fig.6 Node numbers of the damping gap

图7 阻尼通道间隙处磁感应强度曲线，I=1.0 AFig.7 Magnetic induction intensity curve of the damping gap when I=1.0 A

图8所示为给励磁线圈施加1.0 A电流、阻尼通道间隙为2.0 mm时，有效阻尼通道长度和内磁芯半径与有效阻尼通道处磁感应强度的关系曲面。由图可知，随着有效阻尼通道长度增加，有效阻尼通道处的磁感应强度逐渐减小；随着内磁芯半径增加，有效阻尼通道处的磁感应强度逐渐增大，但是增幅较小，说明内磁芯半径对阻尼通道处磁感应强度影响较弱。

图8 电流为1.0 A、阻尼通道间隙为2.0 mm时有效阻尼通道处磁感应强度曲面Fig.8 The magnetic induction intensity at the effective damping gap when the current is 1.0 A and the damping gap is 2.0 mm

3.2 阻尼性能分析

汽车发动机处于start/stop模式时的激振频率在25 Hz左右。因此结合悬置磁路的磁场仿真结果以及阻尼力数学模型，在激振频率为25 Hz、激励幅值为1 mm的条件下，对磁流变悬置工作时的流量变化及输出阻尼力进行了仿真分析。

图9表示磁流变悬置工作时液体流量和激励电流之间的关系。随着激励电流增加，有效阻尼通道处的磁流变液黏度发生如图3所示的变化，由式(1)～(4)可知流经阻尼通道的液体流量非线性减少，同时惯性通道内的液体流量增加，并且它们的流量总和保持恒定。

图10为悬置的输出阻尼力与激励电流的关系曲线。从图中可以看出磁流变悬置的恢复力和可控阻尼力随着电流增大而增大，可控阻尼力的变化趋势与图4所示的磁流变液τy-B曲线基本一致；但是黏性阻尼力随着激励电流增加反而减小。由阻尼力数学模型与图9所示流量的变化曲线可知，随着电流增大，悬置黏性阻尼力与通过阻尼通道流量曲线变化趋势具有一致性，流经阻尼通道的流量减小导致黏性阻尼力减小。

图9 磁流变悬置液体流量与激励电流关系曲线Fig.9 Relationship between the fluid flow rate and the excitation current of the MR mount

图10 磁流变悬置阻尼力与激励电流关系曲线Fig.10 Dependence of the damping force upon the excitation current of the MR mount

图11为悬置阻尼通道间隙、内磁芯半径与悬置恢复力的关系曲面。从图中可以看出，悬置的恢复力随着阻尼通道间隙和内磁芯半径增加而减小。当阻尼通道间隙较大时，内磁芯半径对悬置恢复力的影响较小；随着阻尼间隙逐渐变小，内磁芯半径对悬置恢复力的影响逐渐变大。阻尼通道间隙宽度对悬置恢复力影响较大，当阻尼通道间隙从2 mm减小至1 mm时，悬置的恢复力急剧增大。通过对比图11(a)和(b)，阻尼通道间隙从2 mm减小至1 mm，有激励电流时，结合阻尼力数学模型可知，磁流变悬置黏性阻尼力的增加速度大于可控阻尼力的增加速度，进而使磁流变悬置的可控性变差。

图11 悬置恢复力关系曲面Fig.11 Relationships of the restoring force with the radius of the internal magnetic core and the damping gap of the MR mount

理想的磁流变悬置在低频工况下应具有大阻尼大刚度特性，在高频工况下具有小阻尼小刚度特性。为保证磁流变悬置尽可能满足理想工作特性同时能够具有良好的可控性和结构紧凑性，结合磁流变悬置仿真分析结果可知，悬置阻尼通道间隙不宜过小，并且有效阻尼通道长度和磁芯的径向尺寸不宜过大。

4 试验测试与分析

4.1 磁流变悬置性能试验与分析

在结构设计和理论分析的基础上，加工了磁流变悬置样件，悬置的关键结构参数如表1所示。在液压伺服测试系统(MTS810测试仪)上进行了悬置的性能测试。图12(a)和(b)分别为磁流变悬置实物图和试验测试台。通过致动器提供不同频率的正弦位移激励(振幅为1 mm，激励频率范围为1～50 Hz)，磁场通过外加电流控制，范围：0～1.0 A。如图12(b)所示，阻尼力由力传感器测量，参考初始点的向上位移和拉伸力定义为正方向。

图12 磁流变悬置性能试验图Fig.12 The MR mount and the performance test equipment

图13为在不同激励电流下磁流变悬置的动刚度与频率的关系图。由图可知随着激励频率增大，磁流变悬置的动刚度增大，当激励频率在1～25 Hz区间时，悬置的动刚度迅速增加，激励频率超过25 Hz后，悬置的动刚度增加速度逐渐减小，最后动刚度曲线趋于平稳；当频率与激励幅值不变时，磁流变悬置的动刚度随着电流增大而增大。激励频率为25 Hz、无激励电流时，悬置的动刚度为390 kN/m，激励电流为1.0 A时，悬置动刚度为680 kN/m。因此，该磁流变悬置具有良好的可控性。

图13 磁流变悬置动刚度曲线Fig.13 Dynamic stiffness curve of the MR mount

图14给出了当激励频率为25 Hz、幅值为1 mm、向磁流变悬置施加1 200 N的预载荷时，悬置的恢复力和可控阻尼力变化曲线。悬置的恢复力和可控阻尼力随着激励电流增大而增大。当激励电流为0 A时，磁流变悬置的恢复力主要为橡胶的主簧力和磁流变液的黏性阻尼力，随着激励电流增大，磁流变悬置的可控力增大，当激励电流为1 A时，可控阻尼力达到最大为144.6 N。当激励电流从0.75 A增加至1 A时，悬置的可控力增幅很小，说明该磁流变悬置的饱和电流为0.75 A。

图14 试验结果Fig.14 Test results

图15所示为磁流变悬置输出阻尼力试验和仿真结果对比曲线。当激励电流较小时，悬置输出阻尼力的实验值与仿真值差异较小；随着激励电流增加，输出阻尼力的实验值小于仿真值。造成这种差异的主要原因在于理论计算时假设液体的流动方式为层流，但是磁场对磁流变液的流动特性有较大的影响；另外在磁场作用下，阻尼通道内磁性颗粒由单链状凝聚为柱状，导致理论饱和剪切应力大于试验值；并且悬置的阻尼力数学模型是基于磁流变液Bingham模型推导的，未考虑磁流变液的增稠效应，也会导致悬置阻尼力的实际测试值小于理论值[20]。但是理论计算和试验结果的主要变化趋势有很好的一致性，表明磁流变悬置理论设计方法是正确的。

图15 仿真与试验阻尼力对比曲线Fig.15 Damping force comparison between simulation and test

4.2 Start/stop模式下实车试验

为验证设计的磁流变悬置在发动机start/stop模式下的隔振性能，对装有磁流变悬置车辆的悬置主动侧(靠近发动机)和被动侧(靠近车身)的振动加速度进行了试验测试与分析。图16为实车测试现场。实验设备主要包括：长安某型号乘用车、2个加速度传感器、数据采集与分析系统。2个加速度传感器分别固定在车辆发动机右侧悬置的主动侧和被动侧。试验工况为启动(start)工况和怠速熄火(stop)工况。

图16 Start/stop模式下实车试验Fig.16 Vehicle test in the start/stop mode

图17为车辆启动(start)、熄火(stop)的发动机转速曲线。发动机启动后，其转速迅速升高，在4 s左右达到峰值，达到峰值后转速开始下降，在8 s左右下降到700 r/min并且保持稳定怠速状态；发动机熄火后，转速瞬间下降到0 r/min，此时，发动机停止工作。

图17 发动机start-stop转速曲线Fig.17 Engine start-stop speed curve

通过调节直流电源为磁流变悬置励磁线圈提供激励电流。该试验测试了激励电流为0～1.0 A时悬置在start/stop模式下的振动加速度信号响应。

图18为实车start模式下悬置的振动加速度响应曲线。当激励电流从0 A增加到1.0 A时，发动机悬置的振动加速度幅值逐渐减小，激励电流为1.0 A时的悬置主动侧和被动侧的振动加速度幅值相对于无激励电流时的振动加速度幅值减小了约1/2。对比图18(a)和(b)可以看出，振动信号从发动机传递到车身时，振动加速度幅值也下降了1/2。因此，设计的磁流变悬置能有效地隔离发动机start模式下的振动，并且具有良好的可控性。

图18 Start 模式悬置加速度信号响应Fig.18 The acceleration signal responses of the MR mount in the start mode

图19为实车stop模式下悬置的振动加速度响应曲线。随着激励电流增大，悬置主动侧和被动侧的振动加速度幅值减小程度较弱，仅在发动机熄火瞬间能有效地隔离振动。产生这种现象的原因是发动机处于怠速状态时其振动特性为高频小振幅，由磁流变悬置理想特性可知，该工况下要求悬置具有小刚度和小阻尼，而在熄火瞬间，发动机的转矩变化较大，此时需要悬置具有大刚度和大阻尼来衰减振动。对比图19(a)和(b)可以看出，振动信号通过磁流变悬置从发动机传递到车身时，振动加速度幅值下降了约2/3，因此该磁流变悬置能有效地衰减发动机stop模式下的振动传递。

图19 Stop 模式悬置加速度信号响应Fig.19 The acceleration signal responses of the MR mount in the stop mode

5 结 论

1)设计了一种应用于汽车发动机start/stop模式振动控制的流动模式磁流变悬置，在考虑了激励电流对磁流变液黏度的影响规律和悬置液阻效应基础上，建立了悬置的力学模型。

2)仿真分析了激励电流与磁路的结构参数对悬置阻尼通道处磁感应强度的影响规律和悬置工作时阻尼通道处的液体流量以及悬置恢复力和可控力的影响规律。

3)磁流变悬置的性能试验结果表明设计的磁流变悬置动刚度变化范围为0～290 N/mm，最大可控力为144.6 N，表现出良好的可控性。悬置的性能试验与理论计算比较表明悬置恢复力和可控力曲线实验值与理论值吻合程度较好，表明提出的设计分析方法是正确有效的。

4)进行了start/stop模式下实车试验，对装有磁流变悬置车辆的悬置发动机侧和车身侧的振动加速度进行了测试分析。结果表明提出的磁流变悬置能够有效地衰减汽车发动机在start/stop模式下的大振幅振动和扭矩激励。