基于Bhattacharyya距离的小电流接地故障选线

黄昱皓

(三峡大学电气与新能源学院，湖北 宜昌 443002)

随着城市配电网不断发展，电力电缆在城市配电网输电网络中所占比例不断增加。由于受到外界运行条件和系统内部工况等因素的干扰导致电缆线路发生单相接地故障的比例占配电网系统故障总量的80%左右[1]。小电流接地系统发生单相接地故障一般也可持续运行一段时间，但是在运行过程中可能发展成为多点接地继而发展成弧光接地，造成接地点产生弧光过电压，从而危害相关电气设备的绝缘性能，造成设备绝缘老化，降低设备的运行寿命。快速选出故障线路并消除故障可以保障配电网系统的长期安全稳定运行。小电流接地故障选线从采用的信号量可分为稳态选线法和暂态选线法。

稳态选线法中的典型代表有最大投影差值(Δ(IsinΨ))法[2]，其优点是能够克服电流互感器不平衡电流导致选线失败，但该选线算法不能克服交流电网电压故障或电压互感器断线的影响。此外，该算法还存在需要多次对采集信号样本进行投影变换，计算量较大，造成了故障选线的算法时延。小波包变换利用多次叠代的小波变换分析信号样本的细节部分，可以精确地分析出零序电流波形的突变时刻。文献[3]利用小波包变换自适应确定选线的故障频带范围，从能量最大原理出发求出模极大值所对应的均方根值，以此作为故障选线的依据。经验模态分解是一种在不同频率尺度上度量信号变化规律的处理时变非线性信号的一种有效手段，但是经验模态分解存在频谱混叠的问题，为此集总经验模态分解被提出。文献[4]采用改进的集总经验模态分解获得一种小电流接地系统选线算法，并经仿真验证该选线算法的有效性，但是其选线的门槛值还需要进一步研究。文献[5]综合了谐振接地系统的工频和故障暂态电气信息的故障线路筛选方法，该方法考虑电流互感器或电压互感器的接线方式，比较符合实际现场对选线的要求。文献[6]利用经验模态分解后的零序电流本征函数进行Hausdorff距离计算，在Simulink仿真平台上对所提算法进行了测试，选线结果表明该算法具有一定抗干扰能力，但是其选线的门槛值的确定缺乏理论依据。同样是为了避免经验模态分解的模态混叠问题，经验小波变换EWT可以避免端点效应和模态混叠，还可以从噪声环境中提取信号的本征分量。文献[7]将EWT用在谐振接地系统的故障选线中，获得了较好的选线效果，节约了选线时间，缩短了选线的时延。文献[8]采用傅立叶算法改进最大投影差值法的计算量，同样缩减了选线的时延。

基于Bhattacharyya距离算法对故障后的谐振接地系统出线零序电流进行分析，提出了一种新颖的谐振接地系统故障选线方法。Bhattacharyya距离算法通过直接将电流互感器采集得到三相电流获得的零序电流序列进行等距离剖分后得到其连续概率分布函数，从而考虑了谐振接地系统故障线路的参数随机性，比较符合实际情况。通过仿真分析，发现Bhattacharyya距离比Bhattacharyya系数能够更好地筛选出故障线路，且对外界随机性因素的干扰具有一定免疫能力，因而是一种比较实用的谐振接地系统故障选线方法。

1 小电流故障选线仿真平台

图1 配电网谐振接地系统简化模型

以Matlab/Simulink仿真软件作为10 kV配电网小电流接地系统单相接地故障仿真的平台。如图1所示，该谐振接地系统共有4条负荷出线，分别记为L1—L4。其中，符号T为110 kV/10 kV变比的配电变压器；L为谐振系统的消弧线圈的电感值；R为消弧线圈的电阻值；Rg为非金属性接地的过渡电阻。实际10 kV配电网中，架空线路长度在10～25 km，建模时架空线路均采用单个Π型等值电路级联模型，L1、L2、L3、L4的架空线路长度分别为11 km、14 km、26 km和20 km。消弧线圈采取过补偿方式，且相关参数取为R=25 Ω、L=0.86 H。

作为1个仿真示例，设置1个非金属性故障发生起始时刻设置为0.02 s，经历1个周波后该接地故障被切除。电流互感器的采样频率为20 kHz可以满足故障线路筛选的数据需要。系统的故障电压初相角φ=15°，非金属性故障的过渡电阻Rg=30 Ω，出线L1距离母线侧5 km处发生单相接地故障后，线路L1—L2的零序电流波形变化轨迹见图2，从图2中可以看出，故障时刻故障线路的零序电流发生明显的突变，在数值上故障线路的零序电流幅值明显要大于非故障线路，且从方向上看二者波形极性刚好相反，这说明完全可以根据故障后各条出线的零序电流暂态波形的Bhattacharyya距离测度来区分故障线路和非故障线路。

图2 故障后出线L1—L2的零序电流波形

2 Bhattacharyya距离测度及其在故障选线中的应用

2.1 Bhattacharyya距离测度

Bhattacharyya距离测度[9-10]是基于统计学原理相似度度量方法，该相似度计算方法已经广泛应用于模式识别、图像处理和信号分析等领域中。Bhattacharyya距离不依赖于2个分类样本中相同分量的绝对数量，这是其优于传统相似度计算方法例如余弦相似度、CPC(Constrained Pearson Correlation)算法、MSD (Mean Square Difference)算法等的主要原因。假设p1(x)和p2(x)是样本类w1和w2的连续概率分布函数(Probability Distribution Function, PDF)，那么采用Bhattacharyya距离(Bhattacharyya Distance,BD)测度计算样本类w1和w2的PDF之间的相似度为

(3)

式(3)中的定积分值也称作Bhattacharyya系数(Bhattacharyya Coefficient,BC)[11]，即:

(4)

式(4)中，0≤BC(p1,p2)≤1；当w1和w2的变量X为离散随机变量时，式(4)可以改写为

(5)

Bhattacharyya距离测度在度量直方图相似度时具有很好的计算效果。运用Bhattacharyya距离算法计算2条出线零序电流波形的相似度时，需要将2条出线零序电流采样值转换为2个独立的离散随机变量的概率分布函数p1(x)和p2(x)，继而采用式(3)—式(5)计算2条出线零序电流波形的Bhattacharyya距离。如果2个概率分布直方图的重叠程度越高，表示这2条出线零序电流波形相似度越高，也就是Bhattacharyya距离值BD越趋于0，而Bhattacharyya系数值BC越趋于1。反之，BD值越趋于无穷大，BC值越趋于0。至于选择BC值作为选线判据，还是以BD值作为选线判据，这需要通过仿真测试的结果来决定。

2.2 计算Bhattacharyya距离值

在计算2条出线零序电流的Bhattacharyya距离值前，需要将配电网模型中提取的出线L1和L2的零序电流IL1和IL2采样时间离散序列值转化为计算图像灰度相似度时所用到的离散随机变量的概率分布函数，并得到零序电流波形概率分布直方图。

首先，将零序电流取1个周波(或者半个周波)内的数据窗口进行分析，得到其最大值b和最小值a，即可以将零序电流在区间[a,b]内变化。接着将区间[a,b]等分为n份，每份的区间长度h=(b-a)/n，并依次按照升序将这些小区间编号为1,2,3,…,n，并将其作为分布直方图的横坐标。分布直方图的纵坐标由出线L1和L2的零序电流采样值落入各小区间的个数占总采样点数的百分比构成。具体的处理如图3所示。

从而建立了出线L1和L2的零序电流离散序列的概率分布函数和分布直方图。当出线L1发生单相接地故障时，出线L1和L2的零序电流波形分布直方图(数据窗口长度为半个周波且n=10)如图4所示。从图4中可以看出，故障线路L1和非故障线路L2零序电流波形分布直方图相似度不高。将4条出线之间的BC值和BD值用矩阵表示如下：

图3 零序电流波形区间划分

从BC值和BD值的计算结果可以看出，故障线路与非故障线路、非故障线路之间的BC值相差裕度太小无法构造合适的选线判据；相反，BD值具有足够的选线裕度，可以合理选择门槛值以保证选线的准确性。

3 选线判据构造及流程

通过小电流接地选线装置按一定的频率采样可以获取线路零序电流的离散时间序列{yL(i)|i∈(1,M)}，M表示数据窗长度(半个周波)。在此基础上，按下列步骤计算Bhattacharyya距离值。

图4 零序电流波形分布直方图

a.取2条出线零序电流时间序列的最小值和最大值，并按照从小到大顺序将其等分为n个子区间，并计算落在各个子区间内的采样值占总采样点的百分比p1(x)和p2(x)，x的取值范围是[1,n]内的正整数。

b.按照式(3)—式(5)计算2条出线零序电流波形的Bhattacharyya距离BD(p1,p2)。

c.选择合适的选线门槛值，超过该门槛值则启动选线装置，对于与其他出线的BD值均大于门槛值的线路确定为故障线路，可以予以切除。

4 仿真算例

利用小电流接地系统仿真平台，分析在不同故障初始条件下过渡电阻、故障电压初相位以及故障点距离10 kV母线的距离对谐振接地系统故障选线的影响。为保证Bhattacharyya距离测度对于不同的系统运行工况下均能可靠地筛选出故障线路，从这3个主要影响因子出发研究Bhattacharyya距离或Bhattacharyya系数对选线的特征或优势。Bhattacharyya距离计算中主要涉及离散随机变量的概率分布函数，利用获得的概率分布函数计算BD值或BC值。

4.1 过渡电阻对故障选线的影响

分别选取故障时刻的接地电阻Rg为0、50 Ω、80 Ω和100 Ω，保持故障电压初相角为φ=15°，设置故障点f距离L1线路母线侧的距离为6 km。在小电流接地系统仿真平台中按照选线步骤，计算出接地故障后L1—L4之间的Bhattacharyya距离测度，并将计算结果列入表1中。

表1 不同接地电阻下线路间的Bhattacharyya距离值

通过表1中计算的Bhattacharyya距离测度值可知，故障线路L1与非故障线路的BD值在区间[0.12, 0.23]之间波动，非故障线路之间的BD值在区间[0.01, 0.06]之间浮动。这说明Bhattacharyya距离测度可以在不同非金属性接地条件下准确区分出故障线路和非故障线路，这验证Bhattacharyya距离在故障选线上的适用性和抗干扰能力。

4.2 电压初相角对故障选线的影响

在不同的故障电压初相角φ取不同值的条件下，保持非金属接地的过渡电阻Rg=80 Ω。研究Bhattacharyya距离测度抵抗系统不同运行方式的能力。故障线路L1距离10 kV母线2 km处，在小电流接地系统仿真平台中按照选线步骤，计算接地故障发生后出线L1—L4之间的Bhattacharyya距离值，并将计算结果列入表2中。

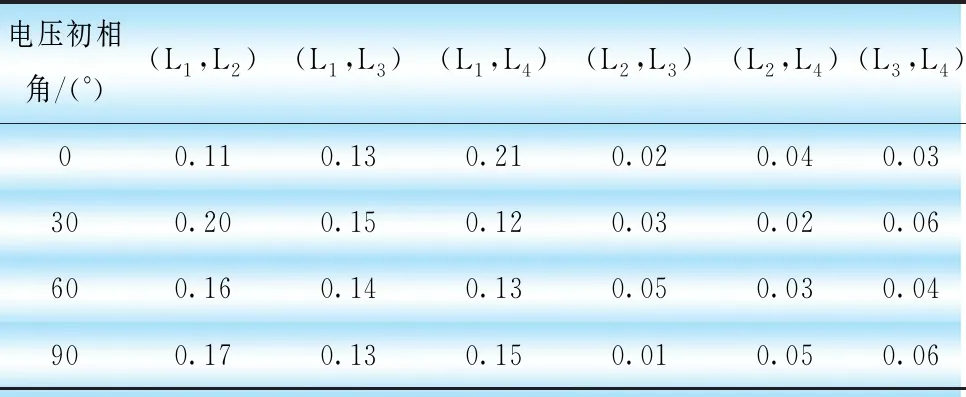
表2 不同故障电压初相角下线路间的Bhattacharyya距离值

从表2的仿真结果数据可知，在不同合闸角下，线路间的Bhattacharyya距离值变化浮动较大，具体表现为故障线路L1和非故障线路之间的Bhattacharyya距离值在区间[0.11,0.21]之间变化，而非故障线路间的Bhattacharyya距离测度值在区间[0.01, 0.06]之间变化，二者之间的差异非常明显，可以设置选线的启动门槛值为0.10，可以保证选线的正确率。

4.3 不同短路距离下的故障选线验证

在不同的非金属性接地故障短路距离下，即故障距离为1 km、3 km、5 km和7 km，接地电阻保持Rg=70 Ω，故障电压初相角保持φ=15°，在小电流接地系统仿真平台中按照上节的选线步骤，计算接地故障发生后出线L1—L4之间的Bhattacharyya距离值，并将计算结果列入表3中。

表3 不同短路距离下线路间的Bhattacharyya距离值

从表3的仿真结果数据可知，在不同非金属性接地故障短路距离下，线路间的Bhattacharyya距离值变化浮动较大，数值上表现为故障线路L1和非故障线路之间的Bhattacharyya距离值在区间[0.12,0.22]之间变化，而非故障线路间的Bhattacharyya距离测度值在区间[0.02, 0.05]之间变化，二者之间的差异非常明显，为此可设置选线的启动门槛值为0.10，可以保证选线的正确率。

5 结束语

介绍一种基于Bhattacharyya距离的谐振接地系统故障选线算法，该算法的优势在于直接根据零序电流的幅值变化规律来判断故障线路和非故障线路。通过建立10 kV配电网小电流接地系统单相接地故障仿真平台，在不同的故障初始条件下，线路之间的Bhattacharyya距离测度值结果表明，该算法具有较好的选线适应性和准确性，是一种比较新颖的谐振接地系统故障选线方法。