机动卫星星座对多区域目标成像任务规划
甘 岚,龚胜平
(清华大学航天航空学院,北京 100084)
0 引 言
对地观测卫星在环境、气象、灾害监测等领域长期发挥着重要作用。为了完成空间任务,常常由多颗卫星组成一个空间系统,即卫星星座[1]。在覆盖全球的对地观测任务中,多颗对地观测星协同的方式能够大大缩短观测重访时间;同时若能充分利用卫星的轨道能力,星座的观测能力将得到更大提高。随着技术不断发展,越来越多具备更强的轨道机动能力的新型卫星投入使用,研究其组成的机动卫星星座的对地观测任务规划问题,成为越来越迫切的需求。
国内外学者在航天器对地观测及任务规划方面进行了广泛研究。文献[2]中提出的方法能够对目标可见性进行快速、准确的计算。文献[3]根据星下点轨迹与区域目标的位置关系,提出了一种区域目标的条带划分方法。文献[4]对深空探测航天器的任务规划方法进行了研究。文献[5]对航天器自主任务规划修复方法进行了分类阐述。卫星任务规划问题已被证明为NP-hard问题[6]。基于该问题,文献[7]等对三类主要的规划算法进行了比较:确定性算法由于本身限制,虽然能解决小规模问题,但是在多星任务规划等大规模问题上,启发式算法和智能搜索算法更加有效。文献[8]提出了一种基于指示的启发式算法(IBMOLS),然而其仅适用于单星任务规划问题,任务规模较小。随着对地成像任务规模的不断扩大,国内外学者针对复杂成像任务规划算法进行了研究。文献[9]研究了可见光和SAR卫星的联合任务规划问题,将其归约为车辆装卸问题,并提出了一种启发式搜索任务规划算法(HADPPEC)。文献[10]针对多星对区域目标的观测任务(SAP问题),将任务规划问题建模为集合覆盖问题,并利用启发式算法进行求解。文献[11]对点目标的成像任务规划进行了研究,对比了模拟退火算法、爬山法和遗传算法的特点。文献[12]将单个空间任务规划问题转化为多个子问题,利用单机调度模型,通过求解这些子问题完成卫星任务规划。文献[13]提出了一种混合遗传算法,通过在模拟退火算法的基础上与遗传算法进行结合,相对于单纯的模拟退火算法结果更优。文献[14]针对遗传算法只能进行全局优化的特点,在种群规模发生改变时适当地切换为局部优化,从而提出了一种新的改进遗传算法。文献[15]在移动目标成像侦测任务中使用了另一种改进遗传算法。
现有研究主要针对单星或多星协同任务,讨论了不同的启发式算法和智能搜索算法的优势,但是缺少考虑卫星进行变轨的情况。本文针对机动卫星星座对多区域目标的成像任务规划问题,首先给出相关约束及优化指标;然后,提出单星单目标观测方法,给出目标可见性及卫星变轨策略;接着,通过条带划分将区域目标观测问题转化为点目标观测问题,建立优化问题模型并给出条带观测策略,利用遗传算法优化星座对多区域目标的观测总面积;最后,通过仿真算例验证算法的可行性和优化效果。
1 相关约束及指标
本文针对特定的星座构型及成像条件,相关约束包括:
1)卫星星座由n颗太阳同步圆轨道卫星组成,共有m个随机分布的区域目标;
2)仅考虑地球J2摄动下的引力场模型;
3)卫星采用脉冲方式变轨,单颗卫星存在最大总速度增量约束,即速度增量Δv需满足:
∑Δv≤Δvmax
(1)
4)卫星变轨后存在返回构型最大时长约束,即返回构型时间tre需满足:
tre≤tre_max
(2)
5)卫星上搭载载荷为光学相机,观测任务存在光照约束,即太阳高度角αh需满足:
αh>0
(3)
6)卫星姿态机动存在最大姿态机动角约束,即姿态机动角αobs需满足:
αobs≤αobs_max
(4)
7)卫星变轨存在最小近地点高度约束,即近地点高度hperigee需满足:
hperigee (5) 8)由于星座已经具备全球绝大部分区域的成像能力,考虑到工程实际,每颗卫星最多执行一次变轨策略,变轨序列x需满足: x={s1,s2,…,sn} (6) 式中:si代表第i颗卫星的变轨策略。 考虑到工程实际,短时间(如24 h)内卫星星座很难实现全球覆盖。在卫星星座对多区域目标成像任务规划过程中,通过变轨使卫星观测到尽可能大的区域目标面积J。该问题可以表示为如下优化模型: (7) 式中:x为优化变量,代表星座的变轨序列;优化的性能指标为最大化观测总面积。 在讨论多区域目标的任务规划问题前,提出单星单目标观测方法:结合解析和数值方法,完成点目标可见性分析;对于不可见的目标,给出变轨策略。单星单目标观测方法在文献[16]中进行了详细阐述,这里只对必要的条件和内容进行介绍,其余不再赘述。 建立如图1所示地心惯性坐标系:X轴由地心指向轨道升交点,Z轴沿地轴指向北极,Y轴构成右手正交系。 图1 解析方法地心惯性坐标系 图1中,S,T分别为卫星、目标初始时刻的位置。卫星在轨道平面内运行,目标则随地球自转沿所在纬线圈运行。考虑一种特殊情况:若当目标运行到轨道平面内T′位置时,卫星恰好运行到目标正上方S′处,即能够对目标进行直接观测。 在二体模型下,将目标所在纬线圈方程与卫星轨道平面方程联立求解,得到T′的坐标及目标由T运动到T′绕Z轴转过的角度θTT′。在此基础上,考虑J2摄动带来的卫星升交点赤经Ω随时间的长期变化,可以求得目标随地球自转到达该点的时间t′T为: (8) 由于卫星最大姿态机动角约束,当卫星处于S′时,卫星存在一个可观测范围,其边界点分别为T″,T‴。以其中一个边界点T″为例,目标随地球自转运动到T″的时间为t″T,由T″运动到T′的时间为tT′T″,如图2所示。 图2 卫星与目标位置关系 卫星运动到成像点S′的时间tS′为 tS′=t1+nS′T1 (9) 式中:t1为卫星从S起第一次经过S′的时间;nS′为自然数,代表卫星第一次到达S′后转过的圈数;T1为卫星运行轨道周期。 在考虑J2摄动的情况下,T1的计算表达式为 (10) 对于一般的情况,目标和卫星运行总会存在一个时间差Δt: Δt=tS′-tT′ (11) 即当卫星运行到S′时,目标并不能恰好处于T′。当卫星运行到成像点S′点时,如果目标运行到边界点T″、T‴之间,则认为目标可见;否则目标不可见,需要进行变轨,使卫星到达成像点S′的时间提前或推迟,从而满足观测条件。那么,可以得到目标是否可见的判定条件为 |Δt|≤tT′T″ (12) 如表1所示,目标的可见性可以具体分为四种情况。 表1 目标可见条件及可见性 在上述解析法的基础上,考虑太阳高度角[17]、地心角、卫星最大姿态机动角度等约束,通过数值方法在ts′时刻附近一定时段内计算目标可见性,可以精确获得目标的可见时段。 在卫星的变轨策略中,主要采用向前、向后相位机动组合的方式进行卫星的轨道机动,以完成对不可见目标的观测及观测完成后返回原构型。 需要注意的是,在变轨时卫星在过渡轨道运行一圈;返回构型时,则通过在过渡轨道运行尽可能多的圈数以节省燃料。在进行相位机动前,需保证卫星有足够的燃料。对于同一目标,卫星的变轨策略是唯一确定的。 对于单个区域目标,考虑以平行于卫星星下点轨迹、等幅宽间隔的多条分割线,将区域目标划分为多个条带[3]。对第j个区域目标,将其分别划分为lj个条带,并按顺序编号。 对任意一颗卫星,如果相邻两条分割线与区域目标上界的交点可见,那么其间所夹的条带可见。这样,将卫星对于区域目标的观测问题转化为卫星对点目标的观测问题。从而可以利用单星单目标观测方法,得到星座对于区域目标各条带的可见性。对于星座各卫星,第j个区域目标中各条带的可见性示例如表2所示。 表2 单个区域目标可见性示例 其中:“1”代表可见;“2”代表不可见但满足变轨约束,卫星可以通过执行变轨策略实现对该条带的观测;“0”代表不可见且不满足变轨约束。 成像任务流程可以描述为:首先,卫星星座确定卫星变轨序列,即各卫星分别选择一个变轨可见条带并针对其进行变轨;其次,各卫星根据条带观测策略选择观测条带;最后,各卫星根据返回构型策略返回构型。在此基础上,将式(7)改写,建立如下优化问题模型: (13) P(x)={pijk} (14) (15) 式中:i为卫星编号,j为目标编号,k为条带编号;wjk表示条带面积;pijk表示条带可见性,可见时其值为1,否则为0;qijk表示卫星是否观测该条带,观测则其值为1,否则为0;P(x)为条带可见性集合,由卫星变轨序列x决定;变轨策略si用各卫星变轨可见条带表示,其对应的变轨策略唯一确定。x为优化变量,其可行域为x∈Vseq,且Vseq为变轨序列集合。优化的性能指标为最大化观测总面积J。 在x确定的情况下,卫星在对区域目标进行观测过程中,需要从条带可见性集合P(x)中选择可见条带进行观测。因此,为使星座观测总面积J最大,需要分析卫星的条带观测策略,即在式(13)中pijk确定的情况下,给出适当的qijk。 当区域目标数超过一定数量时,各卫星的变轨可见条带集Smaneuver规模变大,任务规划变轨序列集合Vseq规模也将随之变得异常庞大。遗传算法(Genetic algorithm, GA)[18]起源于对生物系统所进行的计算机模拟研究。其本质是一种并行、高效、全局搜索的方法。在Vseq中进行变轨序列搜索时,遗传算法相比传统搜索方法更加有效。 基因组用来表示每一颗卫星的变轨策略,采用整数编码方式。每个基因组编码为2位码,包括目标编号、条带编号,可由以下2元组表示: si=[τi,λi] (16) 染色体用来表示变轨序列x,由n个基因组组成,每个基因组编号和卫星编号一一对应,如图3所示。 图3 变轨序列 遗传算法中的适应性为观测总面积J,其计算方法为:对于一条确定的染色体,各卫星针对相应基因组中的条带进行变轨,得到变轨后的条带可见性集合P(x);随后确定卫星的条带观测策略,从而得到观测总面积J。 遗传算法执行过程如下: 步骤1 设定初始种群的大小、自然选择率、变异概率、遗传代数。 步骤2 根据初始种群的大小,随机选择满足变轨约束的区域目标及条带,组成初始种群。 步骤3 对种群中的每一条变轨序列,计算其适应性。 步骤4 进行自然选择、交叉、变异。自然选择采用锦标赛选择方法;交叉、变异的对象均为基因组,交叉方法采用PMX(Partial-mapped crossover)方法;变异方法采用随机变异方法,若发生变异,则从该基因组对应卫星变轨可见条带集Smaneuver中随机选择。 步骤5 重复步骤3~4直至满足遗传代数要求,输出结果个体,即为优化的变轨序列。 由于遗传算法中遗传代数及种群大小为常数,其时间复杂度为常数型;选择观测条带时,由于条带观测策略确定且与卫星数量相关,其时间复杂度为线性型,故本算法时间复杂度为线性型,能够快速地完成变轨序列搜索。 本文对多区域目标成像任务规划方法选取算例进行仿真。相关约束为:单颗卫星最大总速度增量为700 m/s,最大姿态机动角为30°,卫星变轨最小近地点高度为250 km,返回构型最大时长为12 h。仿真环境为3.6 GHz CPU的计算机,编程语言为MATLAB语言。仿真起始、结束时刻分别为 2018-11-07 04∶00∶00(UTCG)、2018-11-08 04∶00∶00(UTCG),仿真时间为24 h。数值方法积分输出步长设置为1 s,如有更高精度要求可以将步长设置为更短。 星座由均匀分布在3个太阳同步圆轨道上的共9颗卫星组成。轨道高度均为500.0 km,倾角为97.4065°,其余轨道根数如表3所示。 表3 卫星部分轨道根数 为便于展示结果,由3个区域目标组成目标集,如表4所示。 表4 区域目标参数 3个目标依次被划分为21、17、17个条带。可见条带集Svisible规模如表5所示。 表5 可见条带集规模 此时,条带观测策略集规模非常庞大,难以用遍历的方法搜索最优条带观测策略。为了对本算法给出的条带观测策略进行校验,在仅考虑目标1、2的情况下,利用遍历方法求得条带观测策略总数为9.05×107,最优解对应的最大观测总面积为3.88×1011m2,耗时1080.84 s;利用本算法得到的策略与最优解相同,仅耗时0.23 s。在给出的条带观测策略接近甚至等于最优解的情况下,本算法极大提高了效率。 分析变轨序列集合Vseq的规模,变轨序列数达到1.13×109。由于遍历1000个序列耗时约1.25 s,若对Vseq进行遍历,估计耗时392.4 h。利用遗传算法在策略集中搜索变轨序列,初始种群大小为100,自然选择率为50%,变异概率10%,经过200代自然选择后得到最终的变轨序列。遗传算法耗时23.00 s,最终规划结果如表6所示。 表6 规划结果对比 由表6可知,进行任务规划后,观测到的区域目标总面积提升约21.02%,所有卫星可见条带总数提升约26.20%。在计算规模上,遗传算法每代只需对100个变轨序列进行操作;同时,每一代50%的种群都被保存到下一代种群中,从而减小了计算规模。本算法同样适用于更多区域目标,且随着目标数目增多、总策略集规模扩大,本算法的效率优势更明显。 本文提出了一种机动卫星星座对多区域目标的任务规划算法。在单星单目标观测方法的基础上,通过条带划分,将区域目标观测问题进行转化,从而建立规划问题优化模型,将任务规划问题转化为序列优化问题。条带观测策略快速可行,遗传算法的优化效率高,星座观测能力得到显著提升。仿真结果表明,任务规划算法使可见条带总数提升约26.20%,观测总面积提升约21.02%。2 单星单目标观测方法
2.1 可见性分析




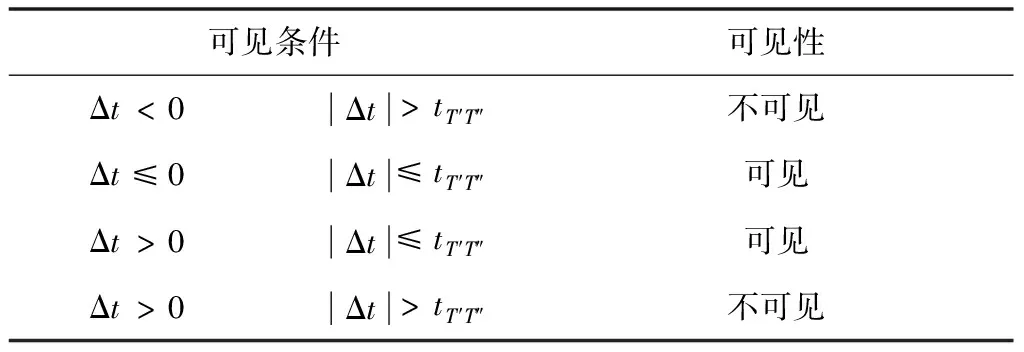
2.2 变轨策略
3 区域目标任务规划
3.1 区域目标条带划分
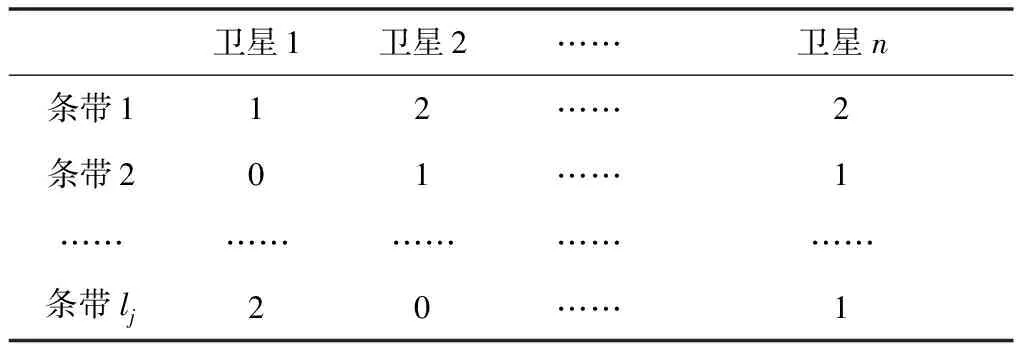

3.2 优化问题模型
3.3 条带观测策略



3.4 变轨序列搜索
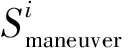

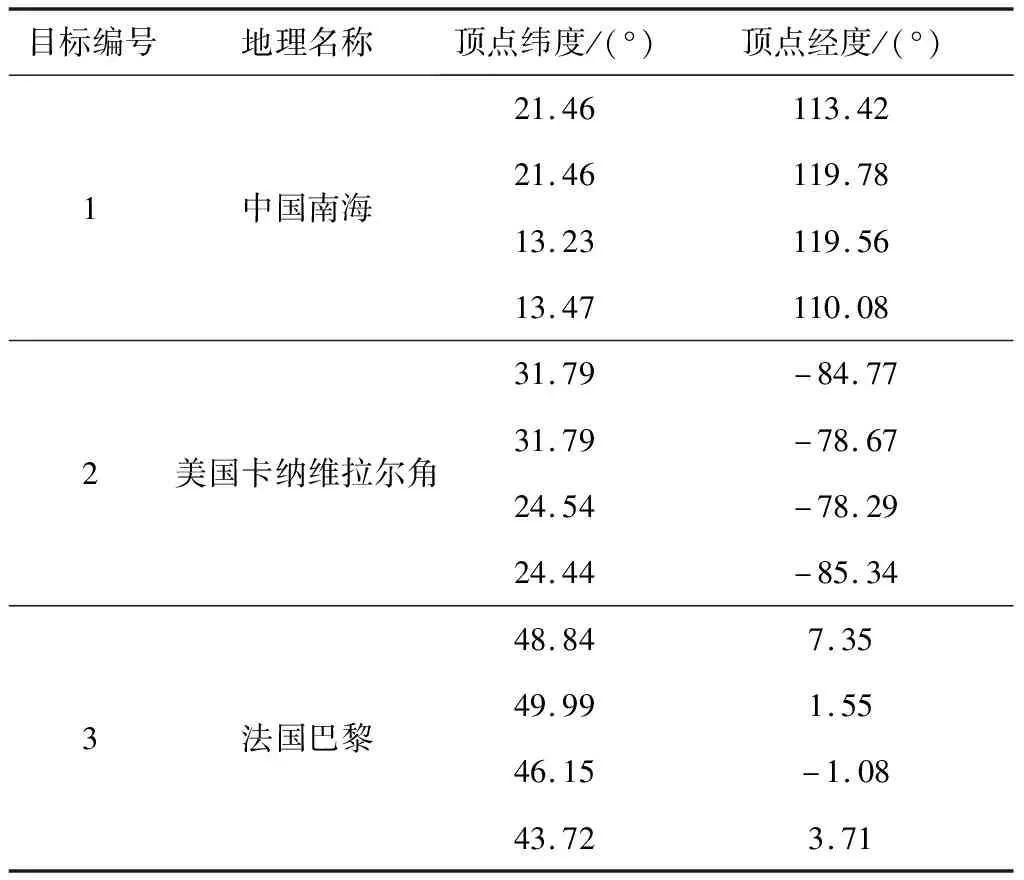
4 仿真校验
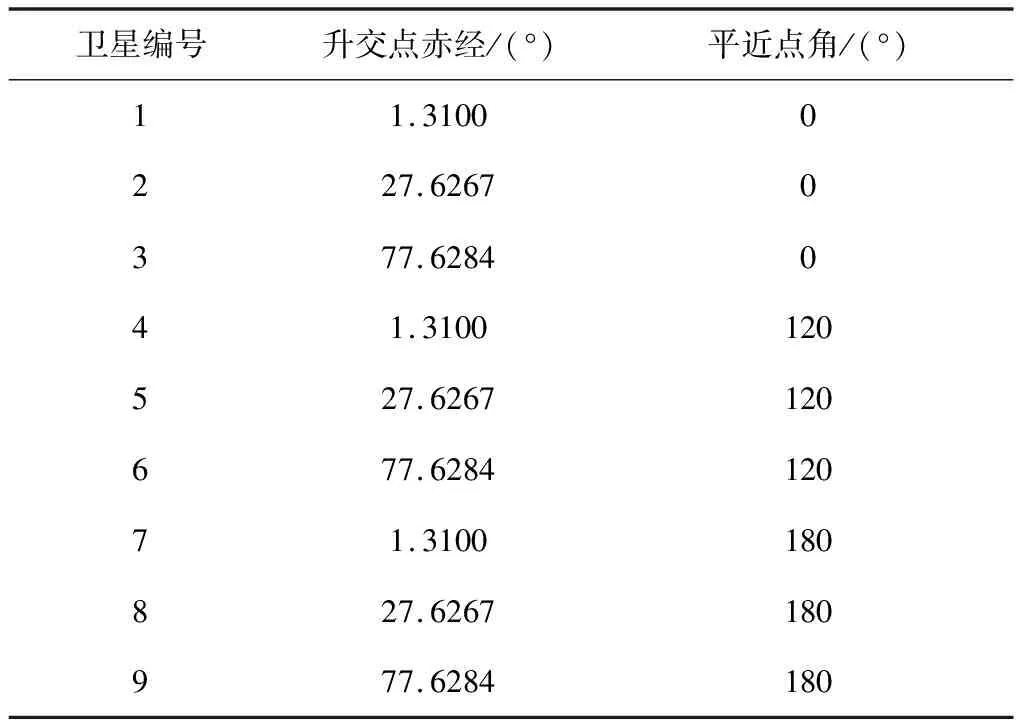


5 结 论

