运载火箭多体动力学建模与仿真技术研究

李 东，杨云飞，胡鹏翔，张 欢,4，程 兴

(1.北京航空航天大学宇航学院，北京 100191；2.中国运载火箭技术研究院，北京 100076；3.北京宇航系统工程研究所，北京 100076；4.清华大学航天航空学院，北京 100084)

0 引 言

2016年6月和11月，我国新一代中、大型运载火箭相继首飞成功。为提高控制能力，新一代火箭采用助推发动机摇摆姿态控制技术，从飞行结果看，火箭刚体、晃动、弹性运动稳定，新型控制方法的正确性得到验证[1]。

新一代火箭模态特性复杂，存在大量助推局部变形为主的模态(如图1所示)。相比传统火箭，新一代火箭有以下特点值得重点关注[2]：

图1 助推局部模态图

1)整体火箭呈现出低频密频模态、强耦合振动、复杂的局部变形等特征，低阶模态中含有大量“呼吸”、扭转、反向弯曲等局部模态，模态特征比单根火箭的模态复杂很多[2-4]；

2)使用大推力发动机导致传动装置-摆动发动机系统的固有频率很低，可能和箭体弹性振动发生耦合；

3)通过助推发动机摇摆，将发动机局部模态引入控制回路。

引入一种合适的分析手段，实现对动力学与控制耦合关系的准确分析，是新一代运载火箭在设计过程中无法绕过去的环节。为此提出了基于多体动力学虚拟样机开展动力学建模与仿真分析的验证新方法。

1 多体动力学技术发展现状

航天器(大型空间站，航天飞机，运载火箭，月球车等)，机器人，高速车辆以及精密仪器等现代工程技术的发展，对大型复杂机械系统的动力学设计与分析提出了越来越迫切的需求。伴随现代计算技术的迅猛发展，多体动力学方法及软件应运而生。总的来说，多体动力学方法将复杂机械系统建模成彼此相互连接的多个刚体或柔性体构成的系统，对其施加各种载荷、约束、接触和碰撞等，进行模拟实际过程的动力学仿真[5]。多体动力学方法以不断发展的数字计算技术为保障，基本不受系统自由度规模和模型复杂度的限制。

多体动力学的发展历程主要可归纳为三大阶段[6-8]。第一个阶段是20世纪60年代至80年代中期的多刚体系统动力学阶段。机械工程领域的需求促进多刚体动力学萌芽并逐步发展成熟。这一时期的代表性研究包括Wittenburg，Haug和Schiehlen等人的工作。同时，涌现出了一批应用广泛的多体动力学分析软件，如ADAMS，DADS和SIMPACK等。

第二个阶段是20世纪80年代至今的多柔体系统动力学阶段。由于生产的发展和生活的进步给工程机械和工业产品的性能提出了越来越高的要求，广泛应用于工业领域的多体动力学方法逐渐发展为多柔体系统动力学。小变形柔性多体动力学最先发展起来并受到研究者们的极大关注，代表性的研究有Shabana和Huston等人的工作。研究者们提出了多种小变形柔性体的建模方法，其中应用最广泛的是浮动坐标系方法和有限段方法。大变形柔性多体动力学的发展始于上世纪末。Shabana等最先提出了大变形柔性体建模的全新方法——绝对节点坐标方法。十多年来，绝对结点坐标方法一直是多体动力学研究领域的热点方向之一。Yakoub等、Shabana等和Von等用绝对节点坐标方法研究了大变形梁的动力学建模，Dmitrochenko等给出了基于绝对结点坐标方法的二维有限元板单元，Gerstmayr等则将绝对结点坐标法引入到三维实体有限元之中。这一阶段出现的较成熟的多体动力学分析商业软件有RecurDyn等。

第三个阶段是本世纪初至今的多场多学科多体动力学阶段。工程实际需求导致多场多学科耦合的多体动力学分析逐渐进入人们的视野。Moller等将多体动力学应用于“流体-结构”耦合的动力学仿真研究。Samin等给出了机电系统的多体动力学建模方法。Liu等分析研究了热载荷作用下的多体系统动力学行为。多场多学科多体动力学的发展方兴未艾，必将使基于数值仿真的动力学设计和分析能力达到空前的高度，促进人类各领域的工程技术不断向前发展。

国内的多体动力学研究始于20世纪80年代[6-8]。刘延柱、袁士杰、黄文虎、陆佑方、洪嘉振、齐朝辉等分别撰写了关于多体动力学的研究专著，针对多体系统的建模方法和数值算法展开了较全面的论述。国内开发的通用多体动力学分析软件并不多见，其中包括上海交通大学洪嘉振等人开发的CADAMB软件以及清华大学任革学等人开发INSIDES[8]软件。其中INSIDES具有针对大规模大变形柔性系统开展仿真分析的能力，该软件在各个系统领域均有较多的应用案例[9-11]，其正确性和稳定性已经得到了工程实际的验证。

2 多体虚拟样机运用到火箭上的优势

2.1 基本思路

典型的运载火箭姿态控制回路原理[12]如图2所示。

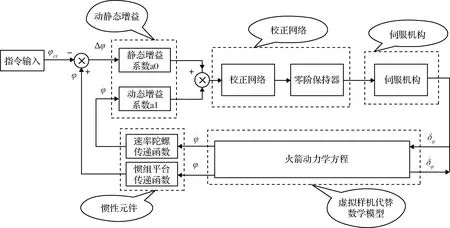
图2 姿态控制回路动力学模型示意

在传统火箭设计，多基于牛顿-欧拉矢量力学推导，获取代数-微分方程形式描述的火箭动力学方程[12]。其中，运载火箭质心平动的动力学方程组为：

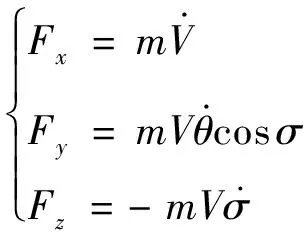
(1)

式中：Fx,Fy,Fz为重型运载火箭在速度坐标系中受到的所有外力，包括重力、发动机推力、发动机摆动惯性力、气动力、气动阻尼力、液体推进剂晃动力以及其他内外干扰力等；m为火箭质量，V为火箭的速度，θ为旋转弹道倾角，σ为弹道偏角。

箭体绕质心转动的动力学方程组：

(2)

式中：Jx,Jy,Jz为箭体绕箭体系三轴的转动惯量。Mx,My,Mz为作用在箭体7上的各种外力对箭体质心的力矩，ωx,ωy,ωz为运载火箭旋转角速率。

采用广义位移算子表达的弹性振动方程为[2]：

(3)

式中：n为考虑的模态阶数。ωi，ξi，qi，Qi和Mi为对应第i阶模态的频率、阻尼比、广义位移算子、广义力和广义质量。

更多关于运载火箭的经典的姿态动力学方程请读者参考相关文献[13-14]。对于新一代火箭，由于弹性模态异常复杂、刚体-晃动-弹性运动交联严重，采用代数-微分方程形式描述的姿态动力学模型会更加复杂[2]，而且模型具有在地面难以验证其正确性的困难。如果采用多体虚拟样机仿真技术，则可以用多体虚拟样机替代上述代数-微分方程(如图2所示)。

基本思路是：采用结构动力学软件(Nastran等)建立火箭结构动力学模型，经过适当转化，生成多体仿真软件可以识别的模型，该模型将自动包含火箭完整的刚体-弹性-晃动运动信息，增加外力函数与控制器后，可以直接驱动虚拟样机仿真。将同等外力条件下，虚拟样机与代数-微分方程仿真结果进行对比，可以实现对模型验证等。采用经过验证的虚拟样机模型，可以进一步开展动力学耦合分析。

2.2 建模原理分析

运载火箭可看成一个弹性体，在弹性体上定义一个浮动坐标系(如图3所示)，当浮动坐标系确定后，弹性体上任意点的运动都可以唯一地分解为浮动坐标系的刚体运动和基于浮动坐标系的弹性运动[5]

图3 弹性体上浮动坐标系定义

r=ro+A(u0+uf)

(4)

式中：r为质点位置矢量，ro为弹性体质心位置矢量，u0为变形前弹性体上质点在浮动坐标系位置，A为浮动系和参考系的转移矩阵。

uf为该点因弹性变形导致的位移在浮动坐标系内的坐标向量，即该点弹性变形的大小。

uf=NTqf=∑Niqfi

(5)

式中：Ni为弹性体第i阶模态振型在该点的取值，qf为弹性体浮动坐标系原点位移弹性坐标(采用模态坐标)。

弹性体上任意点的速度向量可以由位移对时间求导得到：

(6)

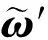
(7)

由于弹性振动还会引起附加的角速度，因此任意点的局部角速度向量为：

(8)

式中：N′i为弹性体第i阶模态振型空间导数在该点的取值。

从分析力学出发建立多体动力学模型，各单元的基本形式为[5]

(9)

式中：T为系统动能，q为广义坐标，Qe为表示广义力；Cq为约束方程；λ为拉氏乘子。

将结构体各个单元的分析力学模型组装，采用大规模的数值求解技术获得数值解，这就是多体仿真的核心思想。

从上述模型基础出发，也可以推导解析形式的全箭整体的姿态动力学模型。

广义坐标系定义为：q=[ro,θ,qf]T，其中，ro=[xo,yo,zo]T为弹性体浮动坐标系原点位移，θ=[γ,ψ,φ]T为弹性体浮动坐标姿态坐标(采用欧拉角表示)。

由任意点速度向量的定义式，可以得到动能的表达式为：

(10)

式中：A，ω′和qf由广义坐标决定，与点的位置无关，可以提取到积分号外，其他积分内的项与广义坐标无关，即与时间无关，是由弹性体本身材料和刚度决定的，与弹性体的运动和受力情况无关，由这些积分项可以定义9个不变量，如表1所示。

表1 不变量列表

根据这些不变量，可以简化动能表达式。同时利用ω′和广义坐标的关系式，考虑飞行中的火箭为双端自由的状态(即无约束)，可以推出火箭的基本动力学方程组，包括平动方程(与ro相关)，转动方程(与ω′相关)和弹性振动方程(与qf相关)。

针对运载火箭，深入的数值分析表明，I0、I6、I5分别在平动方程、转动方程和弹性振动方程中占主导地位，其他不变量在各方程中相对数值很小，可以忽略。其中：平动方程中省略耦合项的影响大小由I2与I0的数值相对大小决定，转动方程中省略耦合项的影响大小由I2，I3，I4，I7，I8与I6的数值相对大小决定，振动方程中省略耦合项的影响大小由I2，I3，I4，I7，I8与I5的数值相对大小决定。数值计算表明：在大型火箭模型中，这些项的数值比一般在千分之一数量级。因此当弹性振动位移和相应的振动速度不是非常大时，可以将这些耦合项略去，从而动力学方程可以退化为解耦的平动方程、转动方程以及振动方程。退化后的方程一般形式如下：

平动方程，即牛顿方程：

(11)

转动方程：

(12)

振动方程：

(13)

注1:由于式(9)中没有引入势能项，因此弹性回复力和阻尼力在方程中都通过广义弹性力实现，即上述方程左端2、3项。

将平动方程在速度坐标系中投影，将转动方程与振动方程进一步分解，同时对刚体运动同样引入线性化假设等[2]，就可以得到与2.1节一致的动力学方程。

上述的推导过程显示，对火箭而言，多体模型本质上和传统的姿态动力学模型是一致的。但由于多体仿真实际上是基于各单元模型(式9)直接展开，因此可以充分体现在解析模型推导过程中被忽略的各项耦合因素的影响。

2.3 引入多体仿真技术的意义

传统火箭设计中所普遍采用的“代数-微分方程组”是对物理本质的高度抽象化，具有形式简洁的特点，理论上具备获取解析解的可能。但是对于捆绑火箭这样复杂的系统，由于方程阶数高、参数多、耦合关系复杂，使得解析解的求解难度大，为了求解必须做大量假设，将模型进行小偏差线性化处理，可能导致设计或仿真结果偏离真实状况。比如，在火箭飞行力学数学模型的推导过程中，对于结构变形要基于小变形假设，建模过程中会忽略各种非线性、强耦合的因素。

如果在数值仿真中采用多体动力学模型替代飞行力学模型，则容易避免飞行力学推导过程出现的错误，获得更加可信的仿真结果。对于模态呈现空间分布特点、助推器和发动机-伺服系统存在局部低频模态，刚-晃-弹运动耦合严重的新一代大型捆绑火箭而言，这一优点显得尤其可贵。与纯“代数-微分方程组”建模与分析方法相比，基于多体动力学虚拟样机模型分析，具有如下优势及特点：

1)多体动力学模型可以使用空间三维结构动力学模型，相比用于传统模态计算用火箭梁模型，表达信息更为全面、准确，更适合于针对复杂结构开展动力学耦合分析；

2)多体动力学模型可实现“复杂结构(含流体)动力学-控制”的一体化仿真，直接仿真推进剂消耗过程，是更为接近物理本质的模型，避免推导数学模型带来的大量简化，完整地保留了火箭各系统之间的耦合关系；

3)多体动力学模型直接基于结构模型进行仿真，能够充分表达全箭复杂的弹性模态特性，没有人为的模态舍弃现象，更没有基于“代数-微分方程”仿真所面临的大量模态排列、模态插值等问题[12]，降低了设计风险；

4)基于多体动力学模型可以方便、直观的提取全箭所有位置姿态与振动响应。通过一次仿真，可以提炼有控制作用下的载荷、晃动幅值，分离体的动态间隙等信息。可以开展关键参数敏感分析，也可以对推力偏差、推力不同步、气动偏差等干扰因素开展更加符合物理本质的仿真，这一点相比数学模型具有很大的优势。

3 新一代火箭多体建模与仿真

要构建一个运载火箭多体虚拟样机模型，需要完成建模包括：结构虚拟样机模型、变质量液体模型、发动机推力模型、分布式气动力模型、导航制导与控制模型、环境参数计算模型等。由于全部的内容非常庞大，本文仅以采用INSIDES软件建模为例做必要的阐述。

1)箭体结构虚拟样机

采用有限元软件Nastran建立火箭结构动力学模型(如图4所示)，然后翻译为多体软件INSIDES识别的语言，转化过程可采用Matlab程序实现。转化完成后形成结构INS文件。有关INSIDES语法，读者可以参考文献[15]。

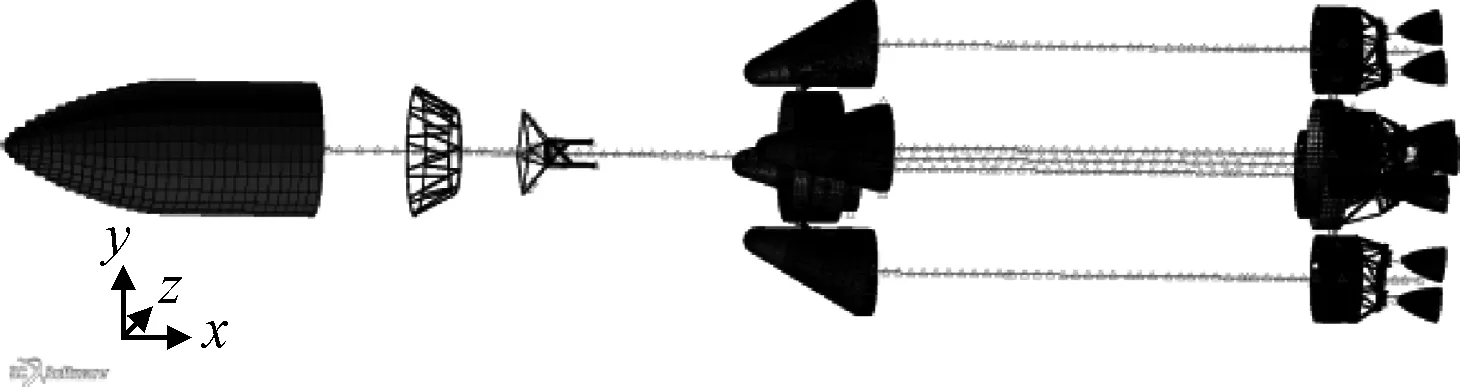
图4 箭体结构模型

多体软件可以对结构有限元模型进行特征值分析，通过特征值校核，可以判断转化过程的正确性[2]。

2)变质量充液贮箱模拟

运载火箭中有90%为液体，液体随推进剂时间快速消耗，如何准确模拟推进剂消耗过程、箭体质量特性的变化，以及质量流动带来的惯性力、哥式力，是多体运用到火箭设计中的一个难点。为此，胡鹏翔等[16]提出了一种全新的多体单元建模方法。

基于文献[16]提供的方法，在多体中建立各个贮箱的变质量单元(如图5所示)。仿真前还需要配置必要的参数，这些参数包括各个贮箱中推进剂随时间变化的液面高度、液体质量、质量变化速度、质量变化加速度、晃动质量与晃动频率等信息。这些参数，可以离线计算出来，然后采用文本文件的方式装订。如果强调对飞行故障或偏差进行实时模拟仿真，则可以将计算液体质量特性的过程编写成一个C++函数，通过DLL方式编译到多体程序中[15]。

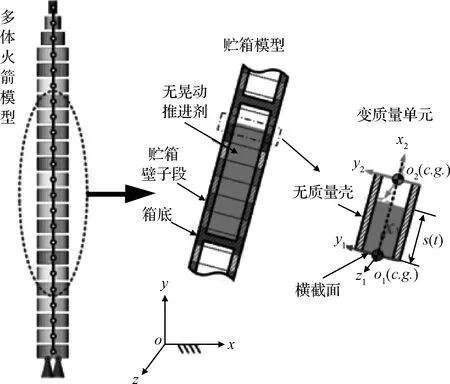
图5 变质量充液贮箱的多体模型

3)推力模型

在多体软件中，通过外力函数方式加入推力。虽然大部分时候，运载火箭推力恒定，但实际上火箭为变推力系统，在点火、大气层飞行、关机、各级转段、过程中，火箭推力会发生变化。为实现推力准确模拟，可以编写推力模拟函数，采用DLL形式编译到多体软件中。

4)气动力模型

在传统的姿态动力学数学模型中，往往采用等效的集中气动力、集中力矩形式模拟气动力作用[12]。

在多体软件中，为模拟火箭真实受力的物理过程，需要采用分布式的气动力系数，模拟作用火箭结构模型上气动力。气动力施加方式的差异是多体仿真区别于一般仿真的一个重大差异。

火箭各部段结构承受分布式气动载荷节点示意如图6所示。

图6 箭体结构承受气动载荷节点示意

考虑气流与风的影响，实时计算各个节点局部攻角αi、βi[12]，则各个节点上三个方向的气动力可写为：

Fx(i)=0.5×CdqSM

(14)

Fy(i)=0.5×CNα(αi)qSM

(15)

Fz(i)=0.5×CNβ(βi)qSM

(16)

式中：Cd为轴向力系数、CNα(αi)、CNβ(βi)分别为法向与横向气动力系数，q为速度头，SM为气动参考面积。由于气动力系数是按照由作用节点所构成的梁段赋值，而多体模型中作用在各个节点上的气动力由前后两个节点承担，故在各节点的气动力表达式前乘以系数0.5。具体实现上，可以采用C++编写DLL程序，实现添加分布式气动力的功能。

5)控制器模型

运载火箭的控制器包括导航、制导与姿态控制功能模块，相关形式请读者参考文献[17-19]。

如果只单独考虑姿态控制作用，则可以将控制方程写成状态空间模型形式，多体软件支持状态空间模型的实现形式，也编写单独的DLL函数实现控制功能。一些多体软件，比如Adams支持和Matlab软件之间的交互仿真[6]。

6)其它

其它待实现的功能，包括从结构虚拟样机上获取特征位置在惯性空间下的位置、速度、加速度、角度信息；计算并输出马赫数Ma、飞行高度H、飞行速度V、大气密度参数；输出发动机摆角信息、关机信息；重力函数的实现等，这些都可以采取多体软件支持的语法与函数形式实现，在此不再赘述。

采用上述方法，实现的一个火箭多体虚拟样机模型如图7所示，其中一组发动机-伺服系统局部放大图形如图8所示。

图7 火箭多体虚拟样机

图8 多体模型(发动机-伺服局部放大)

4 仿 真

针对新一代火箭，采用多体虚拟样机模型与控制参数进行仿真，部分仿真结果如图9～11，仿真显示：

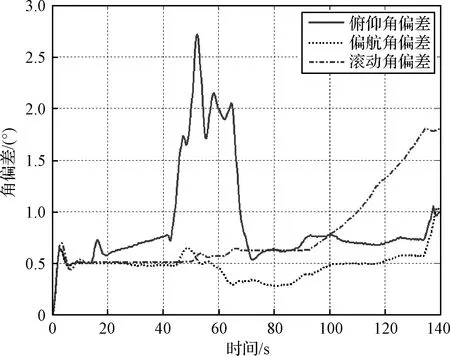
图9 三通道姿态角偏差

1)三通道姿态角与角速度稳定，且姿态变化与传统姿态动力学模型仿真结果一致;

2)全箭弹性、晃动运动稳定，在干扰作用下的振动幅值均收敛；

3)发动机摆角稳定，发动机-伺服系统未现局部的振荡。

基于多体研究方法表明：1)新一代火箭“代数-微分”形式姿态动力学模型正确；2)基于新一代火箭“代数-微分”姿态动力学模型设计得到的姿态控制参数可以确保整个飞行过程姿态的稳定。

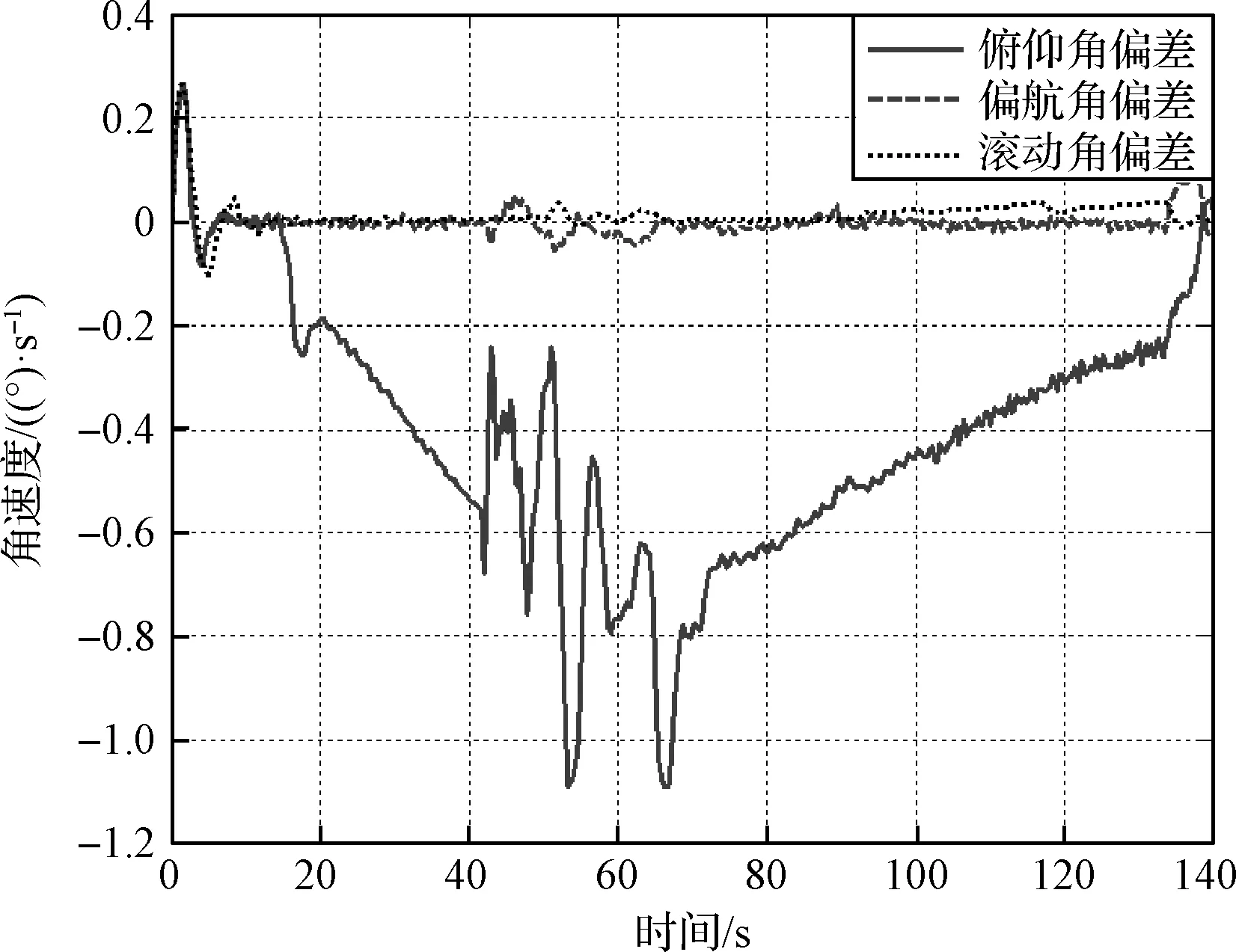
图10 三通道姿态角速度

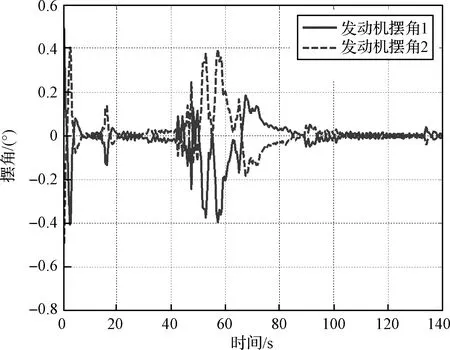
图11 发动机摆角

5 结 论

由于多体仿真技术可以直接驱动结构模型仿真，它在分析弹性与控制耦合类问题中具有突出的优点，可以广泛应用到火箭总体设计中。比如：基于多体技术，可以直接实现控制-载荷一体化仿真，直接输出有控条件下全箭不同部段的飞行载荷，有效解决传统设计中，控制与载荷专业的模型与计算分离、参数包络传递、条件重复考虑等因素带来的结果保守类问题。又比如针对火箭竖立在发射台上从点火到起飞的全过程，或者针对单台发动机在飞行中出现推力脉动的现象，采用多体技术都能很好的实现仿真模拟，在新一代火箭设计中完成的相关工作很好的起到降低飞行风险的作用。

多体动力学虚拟样机仿真方法相当大的程度上规避了传统上完全以“代数-微分”方程描述为特色的建模与仿真方法的缺陷，是一种完全创新的方法，尤其适合对火箭结构动力学特性与控制出现深度交叉耦合问题的开展分析。基于多体仿真方法，可以开展运载火箭总体设计当中涉及到的弹道、控制、载荷、分离、POGO等多专业以及跨专业的一体化仿真[20]分析。可以预计，多体虚拟样机仿真是相关航天器总体设计非常重要的技术发展方向。