定常输入时滞不确定切换系统的鲁棒镇定

刘玉忠, 武挽月

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

切换系统是由一族连续(或离散)时间子系统和一个切换规则组成的系统,在过去几十年中,受到众多研究者的关注[1]。关于时滞切换系统的镇定方面已经取得丰硕的成果,但大多是针对含状态时滞的切换系统,对具有输入时滞不确定切换系统的研究并不多见。

输入时滞现象大量存在于工程实际问题中,因此研究含输入时滞的不确定切换系统具有重要理论价值和实际意义。解决具有定常输入时滞系统的一个比较有效的方法是还原法,借助某种状态变换,将原时滞系统转化为非时滞系统,且Moon[2]指出,在时延很小的情况下,还原法所建立的控制器会使系统具有更好的性能和更小的保守性。

本文运用改进的还原法,研究了一类带有输入时滞不确定切换系统的鲁棒镇定问题。LIN等[3]基于公共Lyapunov函数方法给出了输入时滞切换系统二次镇定的充要条件,但并没有考虑参数不确定性和保守性。WANG[4]利用矩阵的严格完备性设计了一类能使含有输入时滞不确定切换系统稳定的切换策略,但不易实现。本文提出了一种状态反馈控制器的设计方法,依据Lyapunov稳定性理论给出了系统在控制器作用下稳定的充分条件。

1 问题描述及相关引理

1.1 系统描述

考虑如下含有输入时滞的不确定切换系统:

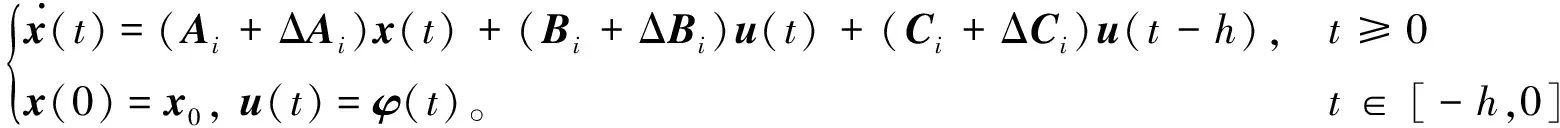
(1)

其中:x(t)∈n为状态变量;u(t)∈p为控制变量;Ai,Bi,Ci为相应维数的常数矩阵;h为控制时延常数;φ(t)是在[-h,0]上的一个可微向量值初始函数;i:+=[0,∞)→M={1,2,…,m}为一个依赖于t或状态x(t)的分段常值右连续切换信号;m为子系统的个数;矩阵ΔAi,ΔBi,ΔCi为时变不确定性参数矩阵[5]。

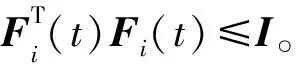
1.2 还原算法

考虑如下带有输入时滞的切换系统[6]:

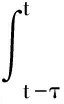
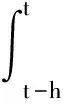
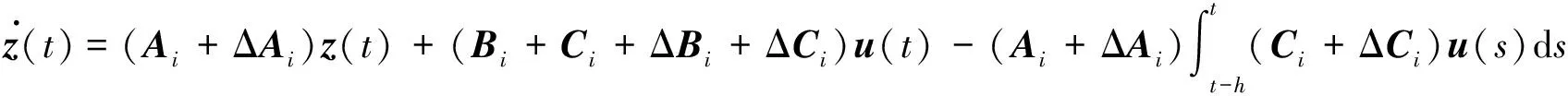
(2)

为了分析和设计系统(2)的鲁棒控制器,需要用到如下引理:

引理1 Jesen不等式[7]

引理2 对于具有相应维数的实数矩阵D,F(t),E,若FT(t)F(t)≤I,则对Ki和∀ε>0,DF(t)E+ETFT(t)DT≤ε-1DDT+εETE。

2 主要结果

针对系统(2),有如下结果:

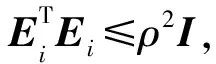
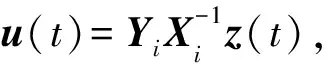
证明 令u(t)=Kiz(t),代入系统(2)有

选取Lyapunov泛函为V(t)=V1+V2[8],则

从上面2个式子可以看出V(t)>0,对V1求导有

再根据引理1和引理2[9]有

对V2求导,有

于是

因为

所以

同理

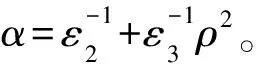
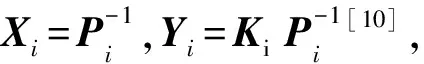
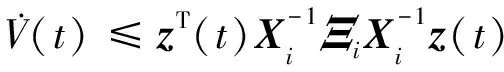
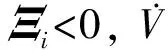
由Schur补引理[11]可知Ξi<0的充分必要条件为Ψi<0,定理得证。

3 结 语

本文研究了一类带有输入时滞不确定切换系统的鲁棒镇定问题[12],应用改进的还原算法,给出了系统鲁棒镇定的充分条件,并把转化为了简洁清晰的LMI形式。