带积分边界条件的三阶微分方程正解的存在性
张红娜, 薛春艳
(北京信息科技大学 理学院, 北京 100192)
考察如下带有积分边界条件的三阶微分方程
(1)
其中:λ>0,是一个正参数;对于1≤p≤+∞,有ω∈Lp[0,1],ω在t=1或t=0处有可能奇异;g∈C[0,1]是一个非负的函数.f和ω满足以下条件:
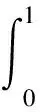
H2)f∈C(R+,R+),R+=[0,+∞),有f(0)=0和对于u>0,有f(u)>0;
H3)g∈C[0,1]是一个非负的函数,对于μ∈[0,1)有

本文主要研究带积分边界条件的三阶微分方程解的存在性,目前也有很多的学者利用上下解、不动点定理等方法来研究带积分边界条件的三阶微分方程。
Sun在参考文献[1]中运用锥拉压不动点定理,得到了带积分边界条件的三阶微分方程单调正解存在性和不存在性的充分条件
其中:λ>0;ω∈Lp[0,1],ω≠0,在(0,1)的任何开区间上成立,并且有可能在t=0或t=1处奇异;f∈C(R+,R+),R+=[0,+∞)和g∈C(0,1)是非负函数。
Fu[2]研究了如下方程解的存在情况:
其中:θ为零元素;g∈L[0,1]非负;φ:R→R递增正同态。
从参考文献[1-5]中不难看出,对积分边值问题利用特征值理论来进行的研究相对较少,特别是正解对参数λ依赖性的研究。
1 预备知识
为了方便,记:
引理1 如果条件H1)~H3)成立,则问题(1)有一个解u,可以表示成

(2)
其中
引理2 令G(t,s)和H(t,s)为引理1中所给出,则有如下结果:
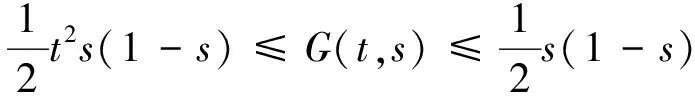
(5)
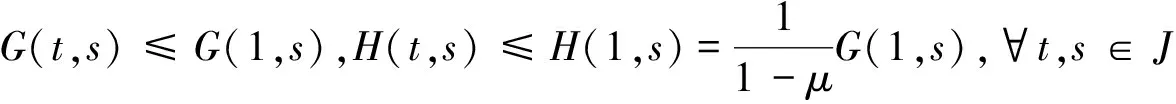
(6)

(7)
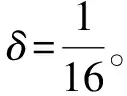
令E=C[0,1],则E是一个实的Banach空间,定义范数为
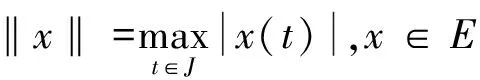
在E中定义一个锥K得
对于r>0,定义Ωr为
Ωr={u∈K:‖u‖ 则有 ∂Ωr={u∈K:‖u‖=r} 定义算子T:K→K为: (8) 引理3[7]如果条件H1)~H3)成立,则T(K)⊂K和T:K→K是全连续的。 ⅰ) ‖Tx‖≤‖x‖,∀x∈P∩∂Ω1和‖Tx‖≥‖x‖,∀x∈P∩∂Ω2 ⅱ) ‖Tx‖≥‖x‖,∀x∈P∩∂Ω1和‖Tx‖≤‖x‖,∀x∈P∩∂Ω2 引理5[11]若D是无限维实Banach空间E中的一个开集,有θ∈D,且P为E中的一个锥,如果算子Γ:P∩D→P是全连续的,并且有Γθ=θ,若满足 则Γ在P∩∂D上关于一个正的特征值有一个固有元,即存在x0∈P∩∂D和μ0使得Γx0=μ0x0。 在本节中,为式(1)的正解存在性建立一些充分条件。关于ω∈Lp[0,1]中的p考虑了3种情况,p>1,p=1和p=∞,其中p>1的这种情况应用到下面的定理中。 定理1 假定条件H1)~H3)成立,若有0 λ=λr∈[λ1,λ2] (9) 其中λ1和λ2是2个正的有限数。 因为0 l1u (10) 因此,对任意r>R0和u∈K∩∂Ωr,有 并且有‖ur‖=r。 另一方面,因为 进而有 即 此外,有 因此有 即 从而计算得出λ1<λ2。 最后,λ∈[λ1,λ2]。定理1证明完毕。 推论1 假定H1)~H3)成立,若满足0 其中 证明 用‖ω‖∞来代替‖ω‖p,便可以证明推论1。 推论2 假定H1)~H3)成立,若有0 其中 证明 用‖ω‖1来代替‖ω‖p,便可以证明推论2。 定理2 假定H1)~H3)成立,若有f∞=+∞,则∃R3>0,使得对于∀r>R3,式(1)有一个正解,且‖ur(t)‖=r。对于任意λ,有 λ=λr∈(0,λ3] 其中λ3是一个正的有限数。 证明 类似于定理1的证明,很容易得到定理2也是正确的。 定理3 假定H1)~H3)成立,若有f0=+∞,则∃r>0,使得对于∀r都有0 证明 与参考文献[6]证明过程类似。 定理4 假定H1)~H3)成立,若有f0=+∞,则∃r1>0,使得对于∀r有0 证明 该定理的证明与定理3的证明类似,在此不予证明。 本文将边界条件推广到了积分边界条件,研究了带积分边界条件的三阶微分方程解的存在性,同时给出解不存在的充分条件以及参数的依赖性[12-15]。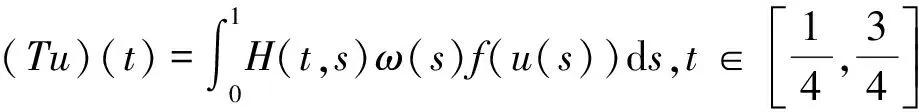

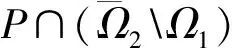
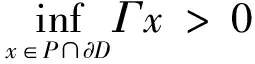
2 主要结论

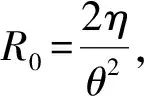
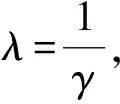

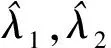
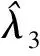


3 结 语

