飞机滑行引起滑行道地基沉降变形分析
邓人铭 ,黄忠凯,b ,陈 颂 ,杜一鸣
(1.同济大学 a.地下建筑与工程系;b.岩土及地下工程教育部重点实验室,上海 200092;2.上海市政工程设计研究总院(集团) 有限公司,上海 200092)
0 引言
在国内,许多机场和飞机跑道均建设在软土地基上,飞机跑道作为一种对沉降要求非常严格的工程,其下方的地基土在飞机起降荷载下所产生的累计沉降会直接影响跑道的舒适性,甚至影响飞机起降的安全程度.因此,对飞机起降荷载作用下饱和软粘土的动力特性进行研究并选择合适的累计塑性应变计算模型,对于准确预测饱和软粘土地基在长期的飞机起降荷载作用下的沉降非常重要.目前,针对饱和软粘土地基累积塑性应变的计算,学者们大多通过实验结合现场实测资料总结得到显式的经验模型.Monismith等[1]最早提出了指数型的经验公式,该公式建立了循环震动次数与土体应变之间的关系.随后,Li 和Selig[2]通过试验发现土体塑性应变与动偏应力和静破坏偏应力之比也存在密切关系,对Monismith[1]的经验模型进行了改进.之后,Chai 和Miura[3]又在Li 和Selig[2]经验模型的基础上考虑了初始静偏应力的影响.周健等[4]通过对日本Ariake 饱和软黏土进行低频循环荷载试验,引入了相对循环应力比的概念,提出了相应的预测模型.黄茂松等[5]又通过引入动偏应力水平考虑了固结方式对轴向累积塑性应变的影响,进一步推广了模型的应用范围.孙玉永等[6]引入等效系数δ将最小动偏应力等效为循环动应力的一部分,建立考虑最小动偏应力的饱和软黏土累积塑性应变计算模型,并进行了验证.韩进宝[7]经过实测数据的验证,采用指数曲线法、双曲线法、泊松曲线法对软土地区的滑行道工后沉降进行分级拟合,表现出的效果较好.张勇等[8]将饱和软黏土的累积塑性应变分为稳定型、破坏型和临界型,并且提出了相应的累积塑性应变方程.目前学者们提出的累计塑性应变的经验模型虽然很多,但是受土体动力特性影响较大,参数选取依赖工程经验,准确度不高.因此建立一种能够结合场地土体实际动力特性的模型来对循环荷载作用下土体的沉降进行准确预测,仍是目前亟待解决的问题.
本文展开了一系列土体室内循环三轴试验,分析了土体轴向累计应变随循环荷载作用次数变化的发展规律.结合数值分析结果和累计塑性应变模型,建立了一种大周次荷载条件下道面地基的沉降预测模型,并利用浦东机场某跑道的历史沉降观测数据对其进行验证.
1 室内循环三轴试验
1.1 试验概况
土样循环三轴试验设备采用同济大学地下建筑与工程系的GDS 动三轴仪.该仪器主要由压力室及伺服主机系统、水压伺服控制加载系统、模拟信号与数字信号控制及转换系统、计算机控制系统4 部分组成,其垂直加载力最大为20 kN,可提供加载频率范围为0.01~2 Hz,设备外观如图1 所示.

图1 GDS动三轴仪
选用原状土作为实验土样进行动三轴试验,土样钻孔采集地点位于上海浦东机场,取样深度为5.7 m 和9.1 m,分别为上海②3-2 层砂质粉土和④层淤泥质粘土,可近似代表浦东机场滑行道下卧土层.根据《土工试验方法标准》(GB∕T 50123-1999)[9]中给出的方法进行制样.
本实验旨在研究机场滑行道下方土体在飞机荷载作用下的动力特性,其应力状态是三维的,且假设飞机滑行所产生的动应力幅值不变,故本试验采用单向等幅应力控制循环加载方式.假定飞机荷载作用形式为半正弦波,为了考虑飞机滑行引起的土体动力特性的变化,在此试验中对土体选定动应力幅值分别为10 kPa、20 kPa,振动频率选定为1 Hz,设置振动次数为5000次.根据《地基动力特性测试规范》(GB∕T 50269-2015)[10]的建议,取弹性应变量和塑性应变量之和为5%作为土体的破坏标准.同时由于飞机荷载作用时程较短,试验采用不排水固结条件.循环三轴试验所采用的工况如表1所示.

表1 循环三轴试验工况
1.2 试验结果分析
对土样进行循环动三轴试验得到了砂质粉土和淤泥质粘土的累计塑性应变-循环次数关系曲线,如图2所示.根据试验结果可见,砂质粉土和淤泥质粘土的累计塑性应变-循环次数关系曲线均为稳定增长型曲线,即加载初期累积应变增长较快,而加载后期累积应变趋于稳定.荷载作用次数达到500 次时,两种土的累积塑性应变都进入了稳定阶段.

图2 累计塑性应变-循环次数关系曲线
总体上看曲线的发展经历了一个上升段后趋于稳定,应变曲线发展全过程可分为三个阶段:
(1)粘弹性阶段.在振次200 次以内,土体受到振动荷载而开始压密,产生粘弹性变形,土体应变随振次增加近似于线性增大.
(2)应变曲线在200~500 振次之间出现转折,进入粘塑性阶段.在振动荷载作用下,主应力方向不断发生改变使土体发生结构性破坏,动应变曲线缓慢增长,而增长速率则逐渐降低.
(3)稳定阶段.在振次达到500 次之后,动应变随着振次的增加而趋于稳定,动应变基本不再增长,曲线最终趋于一条直线.
受GDS 动三轴试验仪器最大加载次数所限,本次试验中只记录了砂质粉土和淤泥质粘土在加载5000 次过程中的累积塑性应变发展曲线.在荷载循环次数达到5000 次时,砂质粉土的累计塑性应变为0.15%,而淤泥质粘土的累计塑性应变为0.36%.可见,由于淤泥质粘土的压缩模量较低、含水率较高,在动荷载作用下产生的累计塑性应变远大于砂质粉土的累计塑性应变.
2 滑行道沉降预测模型及分布规律
2.1 预测模型
由于实际的荷载情况比较复杂,飞机跑道的工后沉降不易准确计算,因而根据经验模型来预测长期的沉降量成了一种有效的计算沉降的方法.基于室内循环三轴试验的结果,不同学者提出了相应的不排水累积塑性应变模型.当然,这些经验模型只适用于土体循环应力比小于临界循环应力比的情况.这些经验模型通常用来预测交通循环荷载下软土地基的长期沉降.
对于不排水累积塑性应变经验模型,Monismith 等[1]最早提出了指数型的经验公式,其具体表达为

其中:εp即为土体累积塑性应变;N为循环振动次数;A和b为经验模型系数.A的物理意义为第一次循环加载时产生塑性应变,与土体类型有关,离散性较大.
随后,Li 和Selig[2]通过试验发现参数A与动偏应力qd和静破坏偏应力qf存在密切关系,将Monismith[1]的经验模型改进为
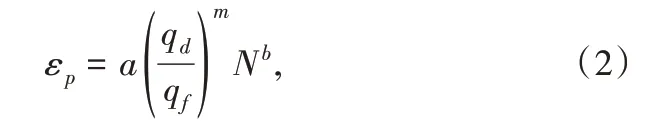
其中,a,m,b为拟合参数.对不同类型的土体,取值有所不同.参数a,m,b的建议值如表2所示.
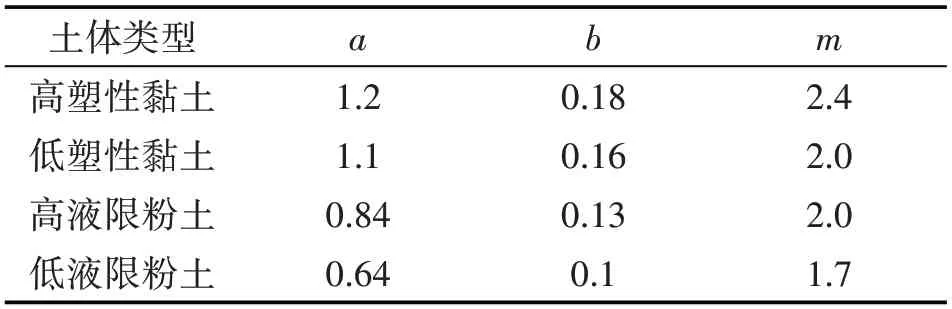
表2 参数a,b,m的建议取值
随后,Chai 和Miura[3]又在Li 和Selig[2]经验模型的基础上考虑了初始静偏应力的影响,将累积塑性应变经验公式改进为

其中:qs为初始静偏应力;n为新增的拟合参数,其他参数与式(2)一致.
本文采用Chai 和Miura[3]提出的累积塑性应变经验模型来预测飞机动荷载作用下滑行道的累积沉降.根据动三轴试验的结果,以表2中的建议取值为初值,拟合得到上述公式中的各个参数值,如表3所示.
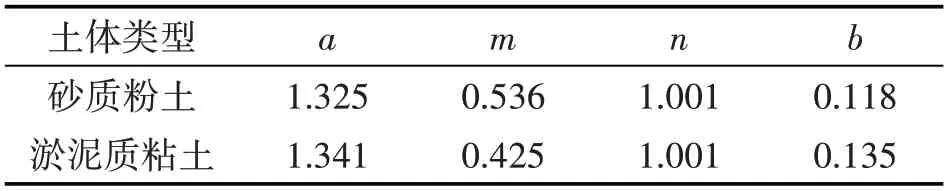
表3 Chai经验模型参数取值
2.2 滑行道道面长期沉降预测方法
为了预测浦东机场滑行道在飞机大周次循环荷载作用下的长期沉降,在已经获得场地土样并进行动三轴试验,且在上述拟合出了累计塑性应变预测模型之后,下一步需要在ABAQUS 中建立飞机—滑行道耦合的三维有限元模型,如图3所示.

图3 有限元计算模型
为了在建模过程中,将飞机荷载视为作用在飞机轮印区域内的面荷载,轮印尺寸为0.5 m×0.35 m的矩形,前轮荷载值为0.5 MPa,后轮荷载值为1.5 MPa.计算飞机单次行驶过程中,土体动偏应力和静偏应力随深度的变化规律,采用分层总和法将土体不同深度处的动偏应力和静偏应力,代入拟合好的累积塑性应变经验模型,最终计算滑行道下卧土层的沉降.
2.3 滑行道道面长期沉降的计算结果
首先通过静力计算,得到飞机—滑行道耦合的三维有限元模型中滑行道下方土体不同深度处的静偏应力qs和动偏应力qd,如图4所示.计算结果表明,飞机荷载引起的下卧土层动偏应力分布随深度的增大呈现出先增大后减小的趋势.动偏应力在地表下方3 m左右处出现峰值是因为飞机荷载并非作用在通道中心,而是沿着中心两侧对称分布.此外,由图4可以看出,飞机振动荷载引起的土体附加应力较小,远小于软黏土的临界应力比,因此根据前文室内动三轴试验的结果可知,飞机振动荷载引起的滑行道道面沉降应表现为稳定型的发展趋势.

图4 滑行道下方土体的附加应力分布图
在得到土体的应力分布之后,为了预测道面的沉降,还需要知道荷载的循环次数.本文中将日起飞航班架次取为1000,这样1月、1年和10年的振次分别为30000、360000和3600000.根据拟合的累计塑性应变预测模型,可以得到滑行道下卧土层在滑行道投入使用后1 月、1 年和10 年的累积塑性应变;再通过分层总和法计算得到滑行道的总沉降.在分层总和法的计算中,将地基土分为6 层,每一层的厚度取为2 m,其中第1—5 层为砂质粉土层,第6 层为淤泥质粘土层,计算公式为

式中:S为地层总沉降;Si为每一计算分层的沉降;εi为每一计算分层的应变值;Hi为每一计算分层的厚度,在此取为2 m.
利用分层总和法,计算得到不排水累积塑性变形引起的沉降如表4所示.预测结果显示,当滑行道使用1个月后,不排水累积沉降为19.8 mm;随着运营时间的增加,滑行道沉降一直在缓慢增长,且增长速率逐渐减缓;当滑行道使用1年和10年后,不排水累积沉降分别为33.8 mm和47.2 mm.

表4 分层总和法计算地表沉降
滑行道长期沉降预测结果如图5所示.可见,在飞机动荷载作用下,变形会随着时间不断累积.同时可见滑行道沉降在工后初期发展较快,在2 年内沉降即可达到35 mm左右.此后沉降随时间增长而趋于稳定,10年后每年的沉降增量都不到1 mm,20 年后的累计沉降预测达到54 mm 左右.得到的沉降发展规律对于实际工程的施工与运营有着一定的参考意义.

图5 滑行道长期沉降预测结果
2.4 预测结果验证
本文所提出的计算模型相比于实际情况进行了一些简化,故计算结果会存在一定的误差.王广德等[11]搜集了浦东机场某跑道的历史沉降观测数据,为了验证该计算模型的合理性,本文将其与本文提出的预测模型的计算结果进行对比.
浦东机场某跑道长4000 m、宽60 m,两侧道肩宽1.5 m.该跑道地基采用垫层及强夯处理,1996 年9 月大面积强夯施工,1997 年10 月地基处理工程竣工.该跑道采用厚度46 cm的混凝土道面,其下为三层18 cm厚的碎石层,结构层总厚度为100 cm.原地面标高约3.5~4.0 m,地下水位埋深约0.5~1.0 m.图6 给出了浦东机场某跑道在飞机荷载作用下的长期沉降观测曲线,其观测时间为从1999 年10 月到2009年4月.
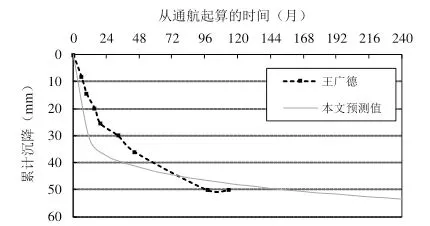
图6 浦东机场某跑道长期沉降观测曲线
由观测数据可知,在飞机长期荷载作用下,浦东机场某跑道在通航初期沉降增长较快,通航1 年后所产生的累计沉降为15.5 mm;而通航后期沉降增长速度逐渐放缓,通航10 年后所产生的累计沉降为50 mm.本文提出的预测模型,1年沉降预测值为34 mm,10年沉降预测值为47 mm.将观测值与预测值进行比较,通航初期的预测误差比较大,而长期的沉降预测结果和实际观测值比较接近.
总体上来看,计算结果与实际观测结果有着相同的发展规律,且长期来看预测结果准确度能够满足工程需求.考虑到飞机滑行道沉降的实际观测过程会受到诸多不可控的环境因素的干扰,实际的沉降观测结果也存在一定的误差.因此,可以认为本文所采用的滑行道长期沉降预测方法与实际观测结果较为吻合,能够为工程的长期运营和维护提供一定的参考.
3 工程建议
根据本文研究得到的结果,提出如下几点工程建议:
(1)根据循环动三轴试验结果显示,砂质粉土的累计塑性应变远低于淤泥质粘土.原因是淤泥质粘土的压缩模量较低、含水率较高,土性较差,在动荷载作用下产生的累计塑性应变较大.因此,在滑行道的设计与施工中有必要格外重视淤泥质粘土层的处理,比如对该土层进行注浆加固提高其压缩模量,或进行抽水降低其含水率,避免其在大周次循环荷载作用下产生较大的沉降.
(2)根据沉降预测计算结果显示,滑行道初期沉降增长较快(工后2年内),此后沉降趋于稳定.因此在机场滑行道投入使用后的2 年内,应注意采取措施控制滑行道沉降的发展,如进行地基加固、采用优化布置的搅拌桩等.
(3)本研究中所计算的滑行道沉降为不排水累积沉降,没有考虑孔压消散引起的土体固结沉降.而实际上在滑行道的长期使用过程中,土层里的孔隙水可能会逐渐排出,产生更大的滑行道沉降.因此,尽管长期来看滑行道不排水累积沉降会趋于稳定,但仍需注意土体缓慢进行的固结沉降,在长期运营过程中要时刻注意土体的排水.
4 结论
本研究通过采集浦东机场滑行道下方典型土样进行动三轴试验,获得了滑行道地基土累计塑性应变随循环荷载作用次数的发展规律,并根据试验结果建立了滑行道长期沉降预测方法,得到以下结论:
(1)砂质粉土和淤泥质粘土的累计塑性应变均呈稳定型增长曲线,曲线的发展经历了一个上升段后趋于稳定.
(2)本文提出了一种数值模拟和室内试验相结合的长期沉降预测方法,先对场地土样进行动三轴试验,拟合累积塑性应变经验公式的参数;再用数值模拟计算不同深度处的土体应力;最后采用分层总和法,计算得到滑行道下卧土层的长期沉降.
(3)根据预测结果,当滑行道使用1 个月后,其不排水累积沉降为19.8 mm,随着运营时间的增加,滑行道沉降增长速率逐渐减缓;当滑行道使用1 年和10 年后,不排水累积沉降分别为33.8 mm和47.2 mm.
——以上海浦东国际机场为例
——结构相互作用的影响分析

