平面几何可变体系探讨

袁良健，王 子，沈天豪

1.中铁第四勘察设计院集团有限公司，湖北 武汉 430063

2.东南大学土木工程学院，江苏 南京 211189

平面体系的几何组成分析是研究平面体系几何稳定性的内容，故又称为几何稳定分析、几何机动分析或几何构造分析。其在结构力学课程的学习中具有重要作用，对静定结构内力计算、力法、位移法、影响线、结构动力学、结构的稳定分析等内容的学习有很大帮助，对实际工程的稳定分析、倒塌分析等具有重要意义。几何组成分析依据的是射影几何学原理，对几何可变体系而言，准确画出可变体系的机动位移图是区分几何瞬变体系和几何常变体系的关键，但机动位移图概念抽象，通常难以直观判断。文章从结构力学教材中对几何瞬变体系和几何常变体系的定义出发，采用假想微小位移的方法，通过具体算例分析二者之间的本质区别，并提出几何瞬变体系优先级的概念，旨在培养学生对抽象概念的直观思维，加强其对基本概念的理解，提高其分析问题的能力。

1 基本判定规则和体系的分类

平面体系可分为几何不变体系和几何可变体系，如图1所示。

图1 体系的分类

平面体系几何组成分析的基本判定规则包括三刚片、两刚片和二元体规则，如表1所示。对常见的平面体系，可采用表1所示的基本判定规则来判定体系的几何组成特性，但对较为复杂的体系，运用基本规则可能无法判断，需另辟蹊径，如采用零载法[1]、等效替换法[2]、假想微小位移法等。其中，零载法运用的是静定结构静力解答的唯一性，仅适用于计算自由度W=0的体系，只能判断体系是否为可变体系，对可变体系无法进一步区分是几何瞬变体系还是几何常变体系[3-5]。等效变换法通常适用于体系中存在复链杆或有多处与其他部分相连的杆件。假想微小位移法通常用来区分几何瞬变体系和几何常变体系，对存在多种位移模态的可变体系，需一一列举判断。

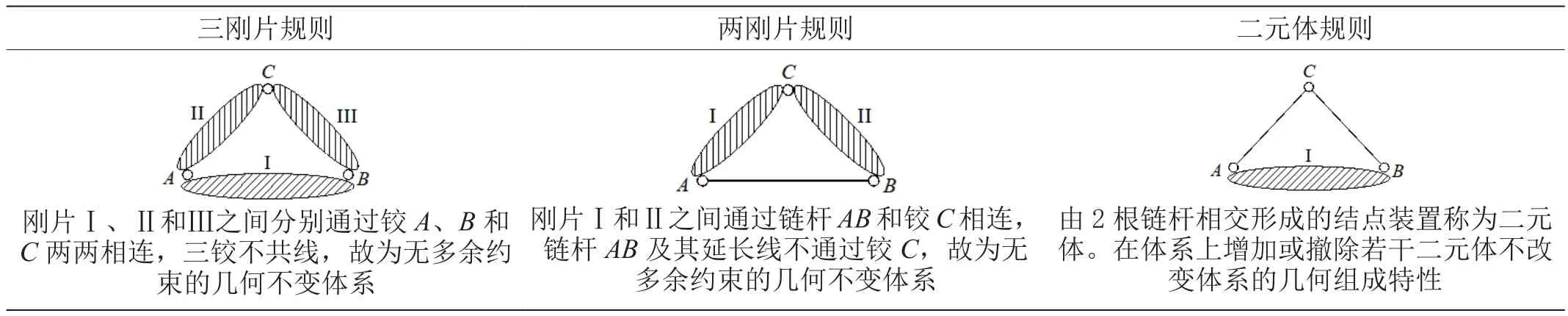
表1 几何组成分析的基本判定规则

2 微小位移和有限位移的区别

瞬变体系和常变体系如图2所示。几何瞬变体系的定义为原体系为几何可变体系，若发生微小位移之后成为几何不变体系，则原体系为几何瞬变体系。如图2（a）所示的体系ABC，若各杆为刚性杆（即忽略杆件的轴向变形），结点B发生竖向位移Δ，杆AB和BC均产生一定的伸长，则如图2（b）所示。

几何常变体系的定义为原体系为几何可变体系，无论发生何种有限位移仍为几何可变体系，则原体系为几何常变体系。如图2（c）所示的体系ABCD，原体系可发生有限位移而变成体系A'B'C'D'，且该位移仍可持续进行，体系A'B'C'D'仍为几何可变体系，故原体系为几何常变体系。

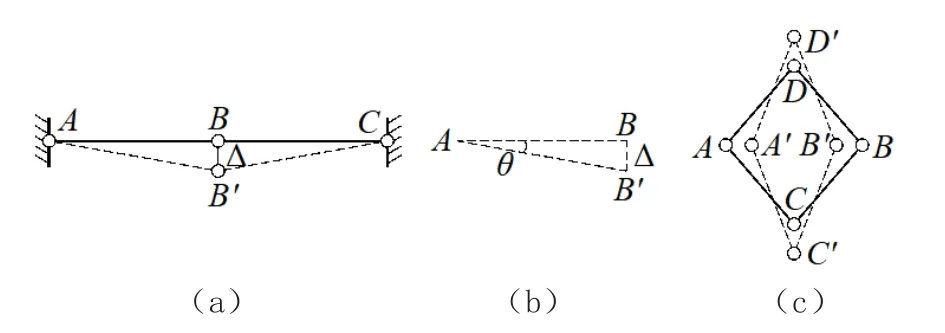
图2 瞬变体系和常变体系

微小位移和有限位移如图3所示。图3（a）所示的体系，假设各杆的长度均为L，且为刚性杆（杆长L保持不变）。如图3（b）所示，当D点发生水平向左的位移Δ时，由此引起B点的竖向位移为δ。

（2）当Δ不断增大成为有限位移时，B点的竖向位移δ是有限位移Δ的同阶量，各杆产生了与有限位移Δ同阶的轴向变形，与刚性杆假定矛盾。易分析得出，图3（b）所示的体系AB'CD'E为几何不变体系，故原体系在D点仅能发生微小位移，为几何瞬变体系。本质上，图3（b）所示体系中D点发生微小位移Δ时，引起B点的竖向位移虽为Δ的高阶小量，但B点偏离原来的位置至B'点，铰A、B'、C不共线，体系成为几何不变体系；D点发生有限位移，各杆必将产生与有限位移同阶的轴向变形，不符合刚性杆假定的前提，即有限位移受各刚性杆的限制而难以发生，原体系为几何瞬变体系。

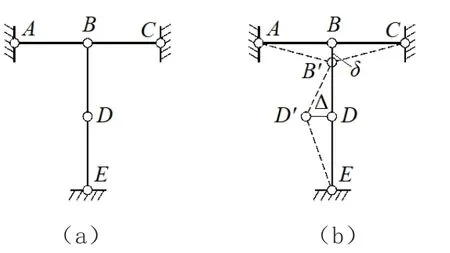
图3 微小位移和有限位移

3 多位移模态可变体系中的优先级

多模态体系如图4所示。图4（a）所示的可变体系存在多种位移模态，两种基本位移模态如图4（b）和图4（c）所示。

（1）图4（b）中刚片DEHI发生微小位移后，刚片ABFG依然可发生微小位移，体系依然几何可变。

（2）图4（c）中刚片ABFG发生微小位移后，刚片DEHI不能再发生微小位移，体系成为几何不变。

（3）其余的位移模态可由这两种基本模态组合而成，如图4（d）所示，体系成为几何不变。由此可知，原体系的众多位移模态中，至少存在一种模态使体系在发生微小位移后成为几何不变体系，故原体系为几何瞬变体系。

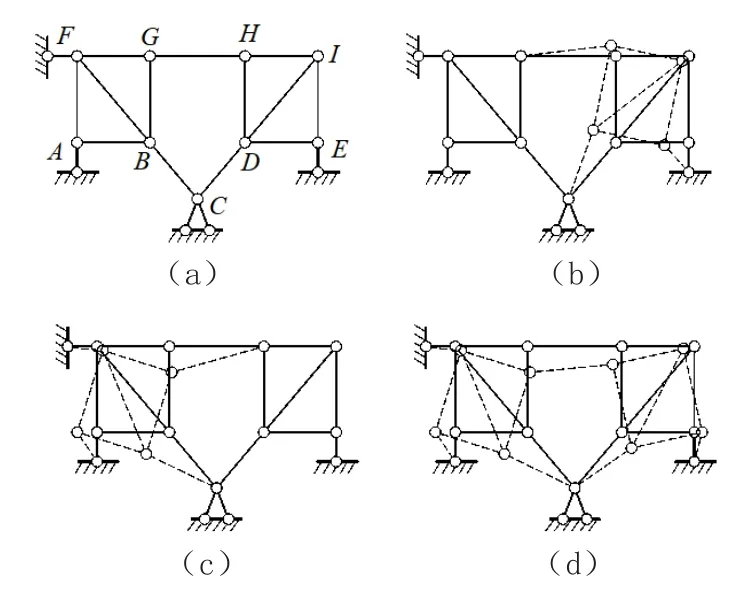
图4 多模态体系

本质上，原体系在无外界干扰时可维持原有的几何稳定；当受到干扰时，体系将寻求新的几何稳定，当新的几何稳定是众多位移模态中产生最小的微小位移时就会成为几何不变体系所对应的情况。若所有的位移模态均无法成为几何不变体系，体系无法维持几何稳定，产生有限位移并持续进行，则原体系为几何常变体系。因此，多位移模态的可变体系中可能既有几何常变的位移模态，也有几何瞬变的位移模态，几何瞬变的位移模态优先于几何常变的位移模态。只要体系发生微小位移后成为几何不变体系，则原体系为几何瞬变体系，几何常变的位移模态只有在所有的微小位移均不能使体系成为几何不变的情况下才会发生。

4 结束语

几何瞬变体系产生的机动位移为微小位移，而几何常变体系产生的机动位移为有限位移，二者从量级上比较，有限位移远大于微小位移，故几何可变体系在产生有限位移之前必先产生微小位移。区分几何瞬变体系和几何常变体系的关键在于，在符合刚性杆假定的前提下，判断体系在产生微小位移之后，能否产生有限位移并持续进行，若不能，则原体系为几何瞬变体系，否则为几何常变体系。对于多位移模态的可变体系，若存在发生微小位移后成为几何不变体系的位移模态，则原体系为几何瞬变体系；当所有的位移模态均不能使体系成为几何不变体系时，原体系才是几何常变体系，即几何瞬变体系优先于几何常变体系。