不确定性负虚系统的绝对稳定性研究
陈 阵
(中国科学技术大学 信息科学技术学院,安徽 合肥 230026)
Lanzon和Peterson最早提出负虚系统这一概念,并且引起了很多系统理论研究者的关注[1-4]。在实际工程中,通过选取合适的系统状态,系统的传递函数将表现出负虚性质,例如大型车队的编组控制、原子力显微镜纳米悬梁臂定位系统、机械硬盘驱动器、Sallen-Key低通滤波器等都可以建模成具有负虚性质的模型[5-7]。负虚系统考虑系统频率响应M(jω)的虚部的性质,要求对于所有的ω∈(0,∞),j(M(jω)-M(jω)*)≥0。
线性时不变(LTI)多输入多输出(MIMO)负虚系统互连的鲁棒稳定性已经被广泛研究[1-2,8-9]。并且,得到了传递函数为M(s)的负虚的被控对象和传递函数为N(s)的严格负虚的控制器的正反馈互连系统(如图1所示)稳定的充分必要条件,即DC增益条件[1]:
λmax(M(0)N(0))<1
(1)
式中,λmax(·)为一个只有实特征值的矩阵的最大的特征值。
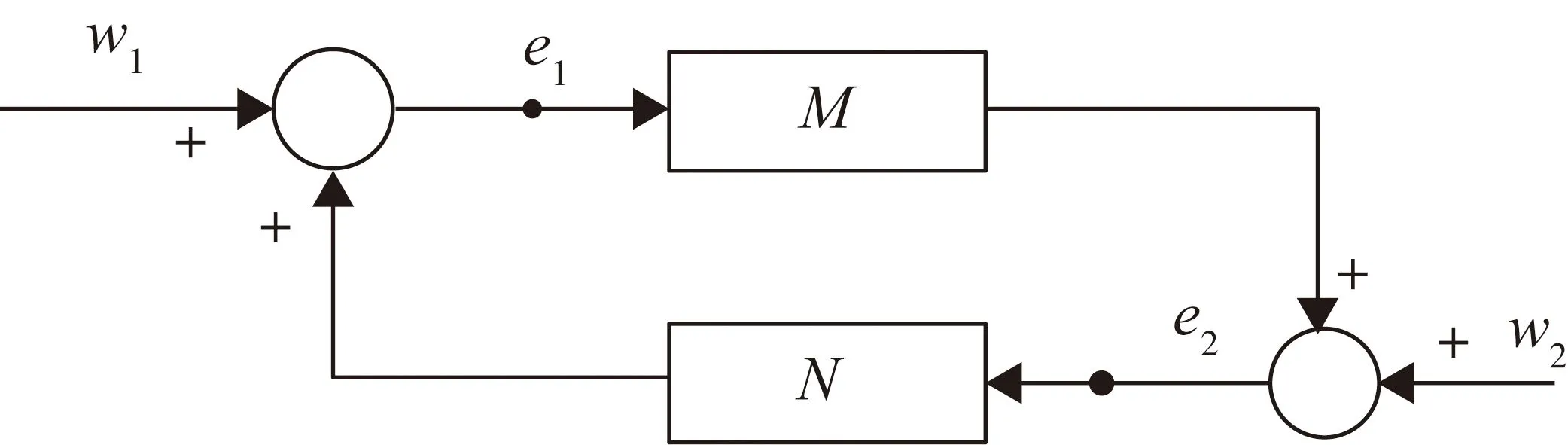
图1 负虚反馈控制系统
近年来,负虚系统理论的研究被拓展到了无损负虚系统[10]、有混合性质的互连系统的稳定性研究[11]、控制器设计和性能分析[12]等各个方面。其中,假设所有状态都可用于状态反馈,针对具有严格负虚不确定性的系统,Song等[12]提出了一种基于状态反馈的系统鲁棒静态反馈综合方法,这是唯一的关于具有非线性的负虚性质的研究,但由于要求非线性部分具有严格负虚性质,具有较高的保守性。
绝对稳定性定理保证了反馈路径包含动态线性时不变系统和反馈路径包含无记忆非线性系统的反馈系统的稳定性。因此,绝对稳定性定理为具有给定集合不确定性的系统的鲁棒稳定性的充分条件[13]。对绝对稳定条件的进一步研究考虑限制在单调的、基于扩展的Lur’e-Postnikov李雅普诺夫函数的斜率有界时不变非线性性[14]。在实际工程系统中,普遍存在着斜率有界的无记忆不确定性,这是影响动态系统性能的一个重要因素[15-22]。因此,具有限斜非线性的系统的绝对稳定性受到越来越多的关注[23]。
本文考虑一个负虚的被控对象,一个斜率有界、无记忆的不确定性和一个严格负虚的控制器互连的系统。提出的定理表明,对于上述系统,如果一些线性矩阵不等式成立,则闭环系统是绝对稳定的。本文使用环变换的方法,扩展了无源性定理的效用。利用这些方法,整个闭环系统采用分解形式。在分解部分的基础上,建立了连通的全局渐近收敛性,并建立了一个Lur’e-Postnikov李亚普诺夫函数,进而验证了系统的绝对稳定性。在负虚系统和不确定性已知的情况下,得到了使系统绝对稳定的严格负虚控制器的DC增益条件。
1 问题描述
1.1 负虚系统
引理1[8]:设(A,B,C,D)是m×m维正则实有理传递函数矩阵R(s)的一个最小状态空间实现,其中A∈Rn×n,B∈Rn×m,C∈Rm×n,D∈Rm×m,则R(s)是负虚的,当且仅当:
① det(A)≠0,D=DT;
② 存在Y=YT>0,Y∈Rn×n,使得
AY+YAT≤0且B+AYCT=0
(2)
引理2[8]:设(A,B,C,D)是m×m维正则实有理传递函数矩阵R(s)的一个最小状态空间实现,其中A∈Rn×n,B∈Rn×m,C∈Rm×n,D∈Rm×m,则R(s)是负虚的,当且仅当:
①A是Hurwitz,rank(B)=rank(C)=m,D=DT;
② 存在Y=YT>0,Y∈Rn×n,使得
AY+YAT≤0且B+AYCT=0
(3)
1.2 斜率有界不确定性
将多个标量斜率有界的非线性以向量形式考虑在一起,将非线性算子的类[25]定义为
(4)
式中,AC(R+)为绝对连续函数f:R+→R构成的空间。由于在变换后的非线性中需要建立一个无源关系,因此提出了扇形变换。
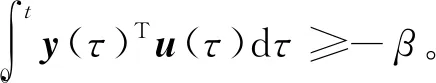
下面的定理给出了斜率有界无记忆的非线性性和无源算子之间的关系。



图2 多个解耦非线性性,M=diag(μ1,μ2,…,μm)
定义2[26]:对于一个由线性系统部分和非线性部分反馈互连的系统,如果对于任意满足扇形条件的非线性性,该系统在原点是全局一致渐进稳定的,则称这个系统是绝对稳定的。
本文研究的是带有不确定性的系统的绝对稳定性,如图3所示。假设外部输入为0,其中x∈Rn,xc∈Rnc;u,y∈Rm,uc,yc∈Rmc。

图3 带有斜率有界非线性性的反馈系统
图3系统状态空间方程为
(5)
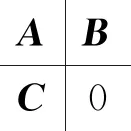
1.3 环变换


图4 环变换后的系统

G~(s)=ABB1C00C10-M-1 00I0I0I00

(6)
式中,M为一个严格正定的对角阵。图4中环变换后系统的状态方程为
(7)


G~(s)=TA~T-1TB~C~T-1D~


(8)


G~(s)=G0(s)+00I-CA-1B100-C1A-1B1-M-100 (s-1I)
(9)

因此定义:
z(t)=x(t)+A-1B1η(t)
(10)
η(t)=ω(t)
(11)
用z和η替换x和ω,则互联系统为
(12)
该互联系统如图5所示。

图5 环变换、卡尔曼标准分解后的系统
该系统是系统(7),即图4分解后的结果。因此,分析系统(5)的绝对稳定性等价于分析系统(7)的绝对稳定性,利用卡尔曼标准分解,转化为分析系统(12)的绝对稳定性。
2 系统稳定性分析
对于由集合Φ的不确定性,负虚的被控对象和严格负虚的控制器构成的系统,给出了系统绝对稳定性的条件和严格负虚控制器的DC增益条件。
定理1:考虑集合Φ的不确定性,令M∈Rm×m,是一个由不确定性构成对角块的严格正定的对角阵,负虚被控对象G(s)的最小状态空间实现为(A,B,C,0),严格负虚控制器H(s)的最小状态空间实现为(Ac,Bc,Cc,0)。则系统(5)绝对稳定的充分条件是:存在对称矩阵Y1,Y2>0使得
(13)
(14)
M-1+C1A-1B1>0
(15)
证明:为了证明系统(5)绝对稳定,只需证系统(12)绝对稳定。令ζ=(z,xc,ξ)T,使用如下的Lur’e-Postnikov李亚普诺夫函数:
(16)

σTξ+ξTσ
=(Az+Byc+A-1B1ξ)TY1z+zTY1(Az+Byc+
ηT(M-1+C1A-1B1)ξ-ηT(C1A-1B1+M-1)Tξ-
ξT(C1A-1B1+M-1)η
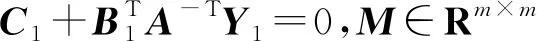
其中,
(17)
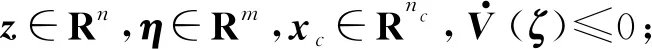
注1:定理1给出了保证系统(5)绝对稳定性的充分条件,这和文献[25]中使用的方法相同,都是环变换。但是,文献[25]研究的是负虚系统的绝对稳定性。定理1给出的是负虚的被控对象、不确定性和严格负虚的控制器的互连作为系统的绝对稳定性。
注2:针对非线性系统绝对稳定性的研究,其绝对稳定性条件建立于线性系统部分已知,非线性部分满足一定的扇形条件的基础上,这也是从实际应用中得到的重要结果。因此,定理1的稳定性判据要求系统满足负虚性质和斜率有界符合绝对稳定性的判定方法。定理1要求已知负虚被控对象、严格负虚控制器和不确定性,但是对于任意满足条件的负虚和严格负虚部分,以及斜率有界这一大类常见的不确定性(如中继、饱和和量化等),该定理都适用。
接下来,考虑严格负虚控制器部分。如果负虚被控对象和不确定性部分是已知并且满足一些条件的,那么严格负虚控制器只需要满足一个DC增益条件,就可以使得整个系统稳定。

H(0)-1+G(0)≤M-1
(18)
(19)
则系统(5)是绝对稳定的。
证明:由定理1的证明,如果T≤0,则系统(5)绝对稳定。显然,由于(19)成立,只需证H(0)-1+G(0)≤M-1,那么(13)成立,则系统(5)是绝对稳定的。
(20)
(21)
因此,
(22)

⟺
(23)
因为ATY1+Y1A≤0,所以式(23)成立。又因为
(24)

注4:推论给出了控制器的DC增益条件,满足这一条件的所有严格负虚控制器都可以使得该系统绝对稳定。也就是说,推论1要求负虚被控对象和不确定性是已知的,但对于广泛存在的负虚系统,只要当不确定性是斜率有界无记忆的,就可以得到其控制器条件。
3 例子与仿真验证
本节给出两个数值例子和仿真结果,用于验证主要结论的正确性与有效性。
例1:考虑图3所示的互联系统(5),不确定性为一维的饱和度:

不确定柔性结构运动的常微分方程为

对应的状态空间方程为

式中,x为系统状态;f为力的输入;q为位移的输出;系统矩阵为

不确定柔性结构如图6所示。

图6 一个轻阻尼弹簧系统

图7 例1系统状态轨迹仿真结果
例2:为了得到严格负虚控制器的条件,负虚被控对象的状态空间实现由下面的矩阵给出:
用YALMIP[28]解线性矩阵不等式条件,得到:
考虑Φ1是一个死区非线性性:
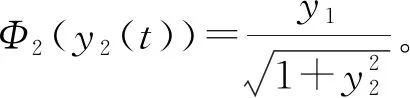
则系统绝对稳定,并在仿真结果图8中得以验证,对于任意一个非零的轨迹初值,随着时间的增长,该系统的状态轨迹都会收敛到0。
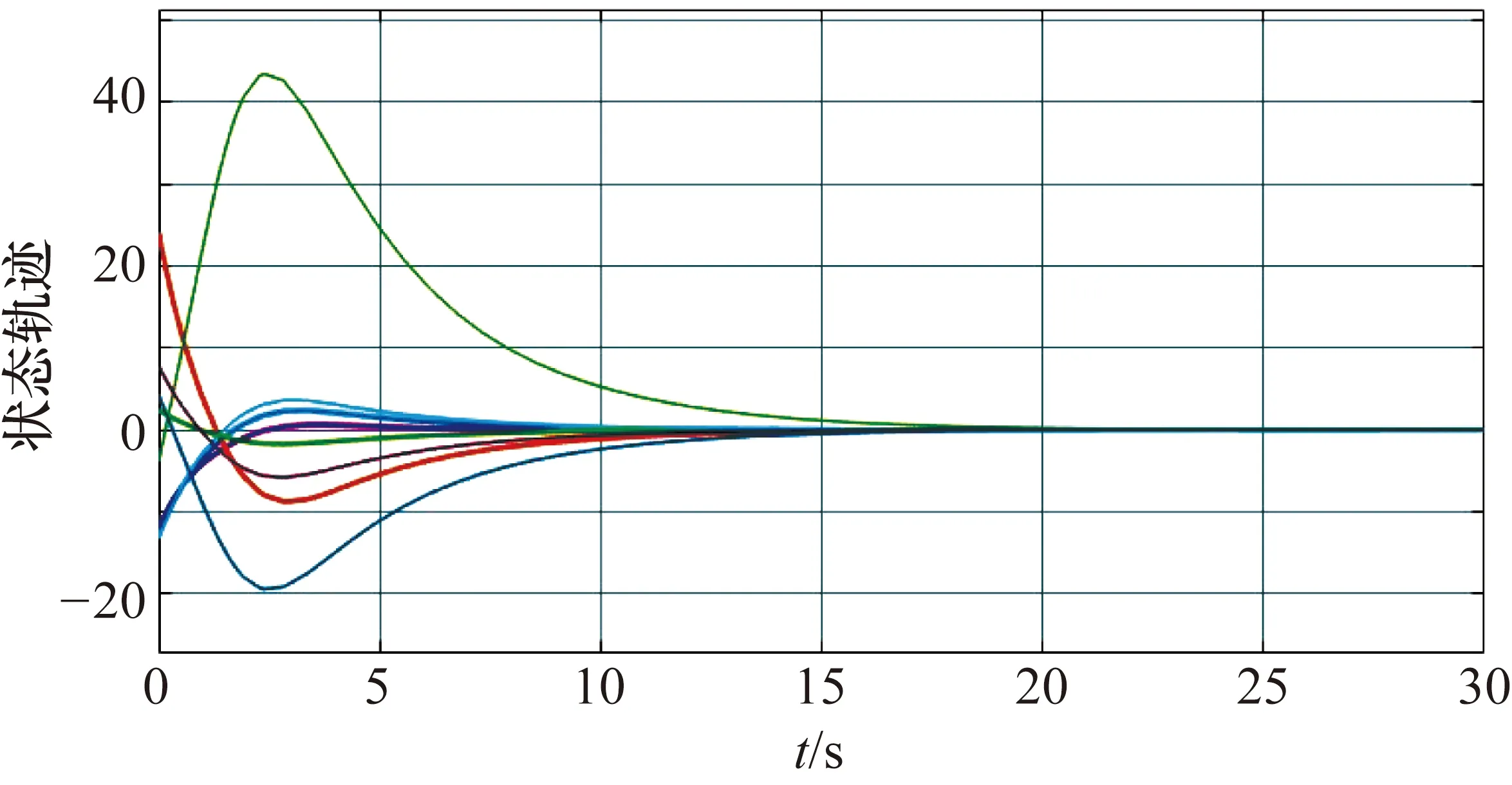
图8 例2系统状态轨迹仿真结果
4 结束语
针对带有不确定性负虚系统互连的绝对稳定性研究的不足,利用环变换等方法研究了负虚系统的绝对稳定性。考虑的系统互连为负虚部分、严格负虚控制器及不确定性,得出了其绝对稳定的条件和控制器的DC增益条件。并在控制器设计部分对主要理论的结果进行了拓展,增加了一定的保守性。因此,这样的严格负虚控制器的设计值得进一步的探索。本文不仅解决了系统的绝对稳定性分析,还得到了设计严格负虚控制器的DC增益条件,具有广泛的应用价值。

