某型惯性测量组合故障传播机理与建模分析

李 强， 吕克洪， 刘冠军， 邱 静

(1.国防科技大学 智能科学学院，湖南 长沙 410073；2.国防科技大学 装备综合保障技术重点实验室，湖南 长沙 410073)

航空机电控制系统中的各单元之间在结构、功能上存在着相互渗透的复杂关系，由于这种复杂关系，一旦某个功能单元发生故障，这种故障信息必将传播给下一个单元，故障沿着系统功能结构进行横向扩散、纵向演化，最终引起整个系统功能的失效[1]。机电控制系统中的故障通常具有复杂多样性、传播性和不确定性等特点[2]，故障的这些特性增加了故障传播过程分析的复杂性，给航空器的安全维护带来挑战。

惯性测量组合是航空机电控制系统中的重要组成部分，主要通过计算航空器的位置、速度和方向来实现航空器的姿态测量和导航[3-4]。惯性测量组合中包含大量电路以及用于测量的传感器，这些传感器和电路受制造精度、振动和温度等航空环境的影响，极易发生故障[5]。又由于惯性测量组合自身高度耦合、相互关联的功能结构关系，使得这些原始小故障易发生传播，进而演化成大故障，最终造成惯性测量组合的功能失效，给航空器带来巨大安全隐患。因此，以某型惯性测量组合为对象进行故障传播模型构建有助于理清惯性测量组合故障的传播机理和影响。

本文根据某型惯性测量组合的功能结构，针对故障传播过程不清晰的问题，分析了该惯性测量组合故障传播路径的复杂多样性和故障传播的不确定性。多信号流图能够描述故障传播的路径，故障扩散强度函数能够解决故障传播的不确定性问题。利用自行开发的“机电系统故障传播建模仿真分析软件”以该型惯性测量组合为对象，建立基于故障扩散强度函数的多信号流模型，并进行可视化的故障传播过程仿真分析，最后用故障注入-故障传播试验验证了模型的准确性。研究结果表明，所建立的模型能够为惯性测量组合故障传播机理分析奠定理论基础，减少航空重大事故的发生，对设备使用人员更好地管装用装具有重要意义。

1 某型惯性测量组合故障传播过程分析

针对某型惯性测量组合故障传播过程存在的两点突出问题(故障传播路径的复杂多样性和故障传播的不确定性)，分别从故障传播路径分析和故障传播不确定性分析这两个方面对航空机电控制系统中的故障传播过程进行机理分析。

1.1 某型惯性测量组合功能结构介绍

某型惯性测量组合是航空机电控制系统中的重要组成部分，用于航空器的姿态测量与导航定位。它主要由电源、滤波放大电路、陀螺、加速度计等9个部分组成。其中陀螺仪和加速度计用于测量空间坐标轴上的角速度增量和线速度增量，最后经A/D转换电路将信息传递给中心信息处理器，从而实现航空器的姿态测量和导航。具体的结构功能框图如图1所示。

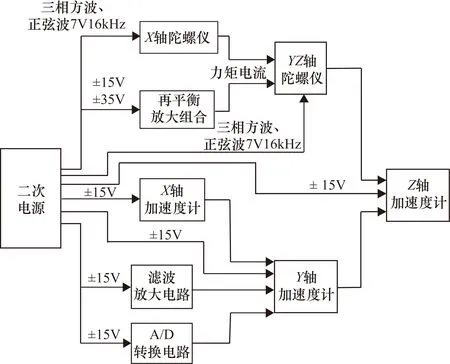
图1 某型惯性测量组合结构图

1.2 某型惯性测量组合故障分析

为了对某型惯性测量组合的故障传播过程进行分析，首先需要明确该惯性测量组合的故障发生位置、故障模式、故障发生概率等信息。在对该惯性测量组合进行FMECA分析的基础上，得到与该惯性测量组合相关的故障信息，分析得到的故障信息数据如表1所示[6]。

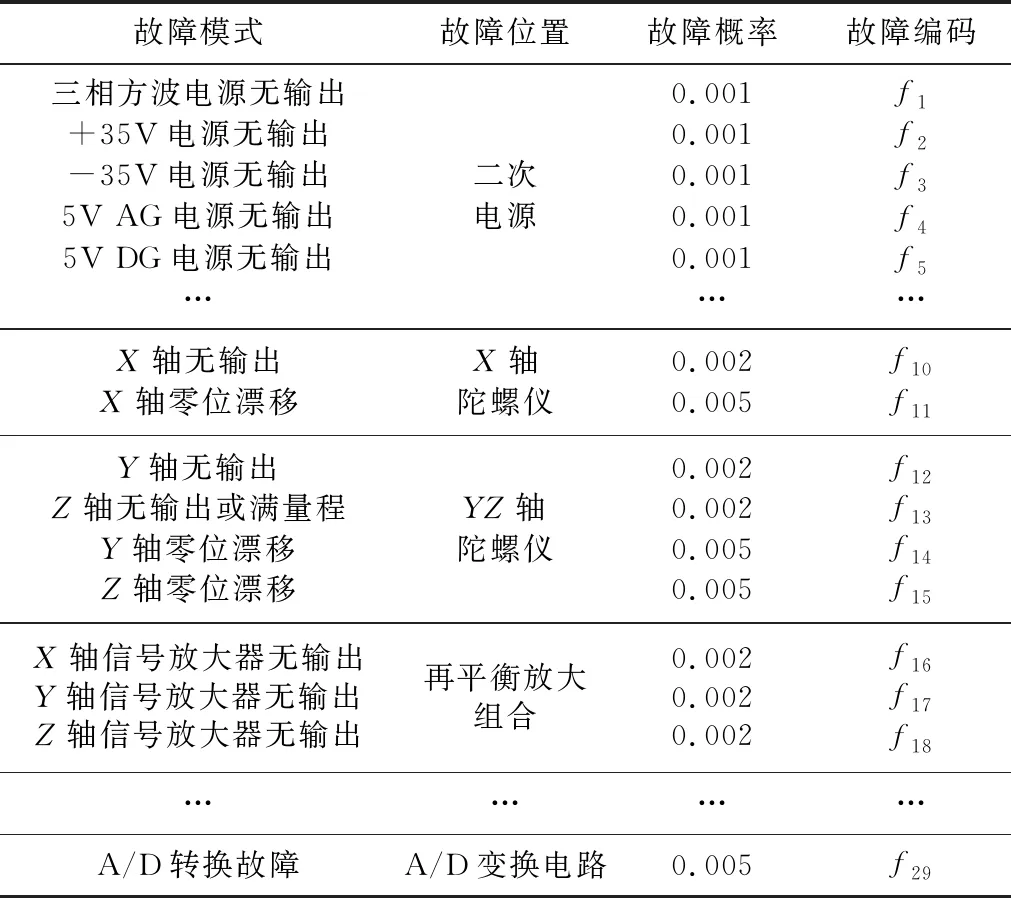
表1 某惯性测量组合故障信息

1.3 某型惯性测量组合故障传播路径分析

通过对惯性测量组合的功能结构进行分析可知，惯性测量组合中含有大量结构复杂的功能电路和高精度的传感器，因此，惯性测量组合中各单元之间的故障传播路径具有复杂多样性，往往不是简单的一对一关系，而是一对多、多对一等复杂关系。一般故障传播路径研究中将故障传播路径分为3种基本形式：汇聚形式、发散形式、冗余形式[7]。为便于清晰地研究惯性测量组合中故障的传播路径，也可引入该方法，例如该惯性测量组合中就存在图2所示的两种故障传播路径基本形式，然后再结合串、并联就可以从传播形式上清晰、全面地描述惯性测量组合中故障的传播路径。

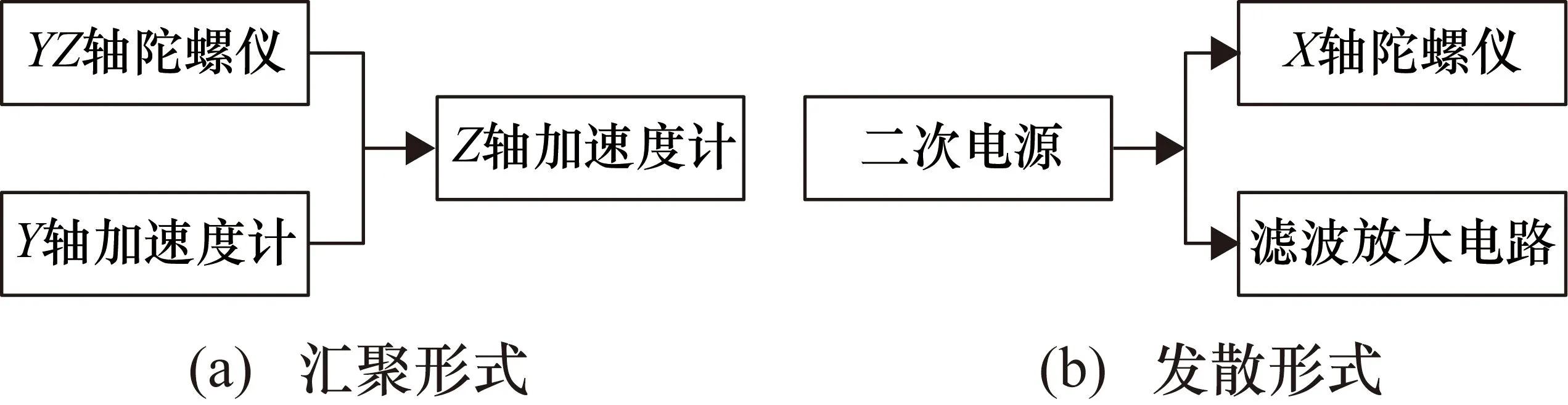
图2 惯性测量组合故障传播路径基本形式

故障在惯性测量组合中传播的本质是异常信号沿着系统功能结构网络进行传播的[8]，因此，可以从故障的这个本质特征入手，将惯性测量组合中的信号分为模拟信号和数字信号，从本质上深入研究惯性测量组合中故障的传播路径。数字电路故障的传播主要按照电路的拓扑路径进行传播，通过研究分析对数字电路故障传播的基本规律进行总结，如表2所示。例如，该惯性测量组合中一次电源和二次电源通过线路连接，当一次电源发生滤波无输出故障时(即发生固低故障)，固低故障沿着线路直接传播，导致整个二次电源发生无输出故障(即发生固低故障)。

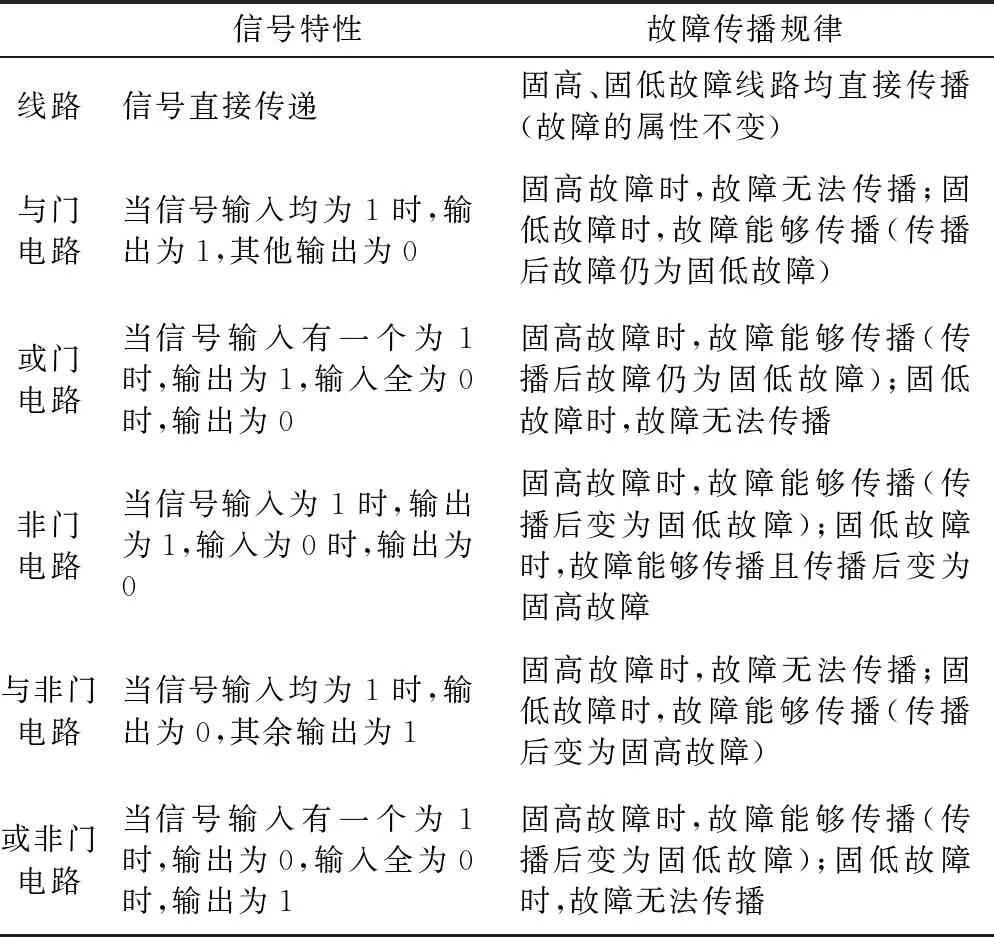
表2 数字电路故障传播基本规律

模拟电路的结构设计决定了信号的流向，因此，模拟电路的故障传播路径与结构设计密切相关[9]。模拟电子线路的故障传播，如图3所示，该惯性测量组合中，当一次电源断路时，将造成X轴陀螺仪、X轴加速度计、A/D转换电路无输出，但是当X轴陀螺仪无输出时，并不会影响A/D转换电路。模拟电路中的电子元器件的故障传播规律也与电子元器件的功能结构设计相关，例如：该型惯性测量组合A/D转换电路中的电阻器不会发生频带故障，但是能够传播这种故障，并且能向任意非低阻抗节点端传播一般故障；当A/D转换电路中的电容器发生故障时，它可以向任意非低阻抗节点端传播交流故障；当该型惯性测量组合中的X轴陀螺仪再平衡放大组合仅发生一个故障时，该故障不能向低阻抗节点端进行传播。

图3 惯性测量组合一次电源断路时故障传播有向图

对故障传播路径进行分析可知，借鉴信息论的相关思想，用多信号流的方式可以对故障的传播路径进行很好的描述。

1.4 某型惯性测量组合故障传播不确定性分析

在实际工程环境中由于温度、湿度、振动等环境因素的不确定性，通常会使系统中关键元器件的参数、单元间的连接系数等发生变化[10]，这些因素都会造成故障传播路径的不确定性。故障传播路径的不确定性可以根据故障的传播形式分为两类：① 具有连接关系的两个单元之间并不一定会发生故障传播关系，如图4所示，虽然X轴陀螺仪与YZ轴陀螺仪之间存在功能关系连接，但是当X轴陀螺仪发生X轴零位漂移故障时，故障不一定会传播给YZ轴陀螺仪(X轴零位漂移故障与时间长短有关)；② 当某个单元发生故障时，由于故障影响度甚小，导致故障不一定能够发生传播行为，但是当多个单元发生故障时，由于故障的累积效应，导致故障能够往下节点传播。如图5所示，由于振动等环境因素使Y轴加速度计发生零位漂移故障，尚未引起Z轴加速度计发生零位漂移故障，但是当YZ轴也发生零位漂移故障时，使得Z轴加速度计也发生了零位漂移故障。

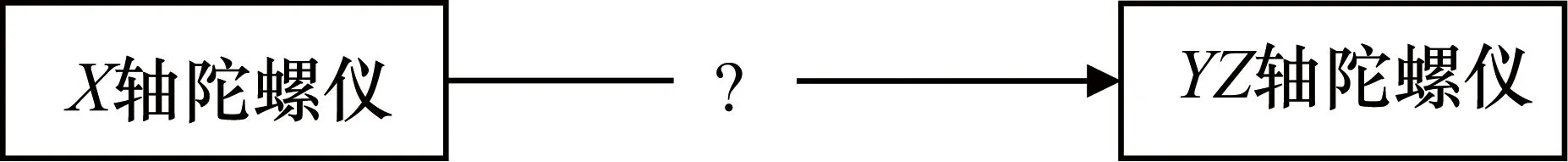
图4 故障传播不确定性形式1

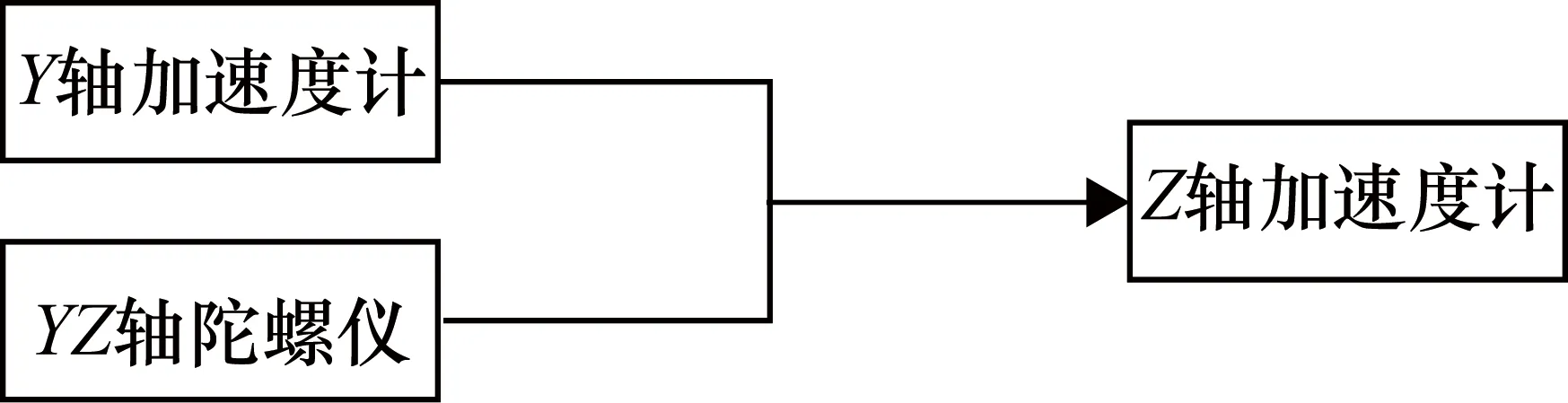
图5 故障传播不确定性形式2

传统的故障传播关系通常仅分为两种：当两单元间不能发生故障传播关系时用0表示；当能发生故障传播关系时用1表示。这种描述方式忽略了故障传播过程的不确定性。为了充分考虑故障传播过程中的不确定性问题，可以引入故障扩散强度函数进行定量分析。故障扩散强度函数能够表征故障的传播能力，故障节点间的扩散强度函数越大，故障越易通过该节点间的路径进行传播[11]。

2 某型惯性测量组合故障传播建模与分析

针对某型惯性测量组合故障传播过程中存在的两点突出问题，在故障传播过程机理分析的基础上，采用多信号流图的思想解决故障传播路径的复杂多样性问题，采用故障扩散强度函数解决故障传播的不确定性问题。下面将以某型惯性测量组合为对象，利用自行开发的“机电系统故障传播建模仿真分析软件”构建基于故障扩散强度函数的多信号流模型。

2.1 多信号流图模型

多信号流图模型在系统分层的基础上，考虑节点间信号的传递关系，能够较好地描述故障在系统中的传播关系，多信号流图的描述元素包括：模块集、故障模式集、故障集、有向边集[12]。

2.2 故障扩散强度函数

当惯性测量组合中某个单元发生故障fi时，故障能否传播到下一单元引起故障fj与3个因素有关：故障fi发生的概率水平、故障fi的强度、故障fi与故障fj之间的关联度。因此，在对某型惯性测量组合故障传播过程进行分析时，引入故障扩散强度函数I来综合考虑这3个因素，进而刻画故障传播路径的复杂多样性和故障传播的不确定性。两节点间的故障扩散强度表征节点间故障的传播能力，当故障扩散强度越大时，故障越易在两节点间进行传播[13]。

节点间故障扩散强度的求取方法具体如下。

(1) 相邻两节点间的故障扩散强度采用单步故障扩散算法求取[14]。

Ii,j=piwidi,j

(1)

式中，Ii,j为相邻两节点(对应的故障为fi与fj)之间的故障扩散强度函数值；pi为故障fi发生的概率水平，该值的大小与故障的故障率密切相关；wi为故障fi的强度，故障强度表示故障发生的强弱，具体的故障强度需要根据故障的信号或征兆来确定；di,j为故障fi与故障fj之间的关联度，其值与两故障所对应的节点之间的物理连接或逻辑耦联有关(受环境等外界因素影响，例如振动环境使两节点之间的物理连接度发生变化)。

(2) 任意两节点间故障扩散强度I通过累积求和的方法求取。

在求得相邻两节点之间的故障扩散强度函数值Ii,j后就可以根据任意节点间的串、并联关系求取任意两节点之间的故障扩散强度值(故障传播节点间串、并联关系如图6所示)。

图6 故障传播的串、并联路径图

① 如果多个节点之间存在串联路径关系，两节点间的故障扩散强度函数值为所有相邻节点扩散强度的乘积，即可表示为

(2)

式中,j=i+1，为故障节点Vi与Vj为两相邻节点；n为第k条串联路径上的节点个数；Ik为两节点间第k条串联路径上的故障扩散强度和。

② 如果多个节点之间既存在串联路径又存在并联路径关系，两节点间的故障扩散强度函数值在求得其串联路径部分故障扩散强度的基础上再将并联部分进行相加，即可表示为

(3)

式中,m为并联路径的条数；I为串、并联路径共存的任意两节点间的故障扩散强度值。

基于上述串联和并联结构的传播路径分析和扩散强度计算，最后对结果进行归一化处理，得到统一尺度下故障扩散强度函数。

2.3 基于故障扩散强度函数的多信号流模型描述

基于故障扩散强度函数的多信号流图组成元素的具体描述如下。

① 系统的功能模块集合M={m1,m2,…,mn}，系统的功能模块根据系统的功能结构进行划分(例如图1对某惯性测量组合模块的划分)。

② 故障节点集N={n1,n2,…,nm}，其中nm表示所有的故障节点个数。

③ 故障模式集F={f1,f2,...,fm}，假设每个故障节点对应一种故障模式。为故障fi定义3个属性：pi(fi)为故障fi发生的概率水平；wi(fi)为故障fi的强度；PF(fi)为故障fi可能传播的故障模式集，通过分析系统中与故障fi所在单元节点存在功能结构关系的单元得到。

④ 有向边集E={ei,j},(1≤i,j≤n)，有向边表示故障节点间的连接与传播关系，即由故障fi传向fj。为有向边定义2个属性：di,j为故障fi与fj之间的关联度，与节点间的信号关联度有关，同时还受外界环境影响；Ii,j为故障fi与fj之间的故障扩散强度函数，其值为Ii,j=piwidi,j。

通过判决条件:I>L(阈值，由故障专家给出)是否成立就可以得出故障在两节点间是否发生传播关系，当条件成立时，说明存在传播关系，否则不存在。

2.4 建模与分析

自行开发的“机电系统故障传播建模仿真分析软件”充分考虑了机电控制系统的层级结构，具备分层建模的能力，同时考虑逻辑与、开关等复杂结构情况，可以进行可视化的故障传播过程仿真分析，同时，该软件还具备机电控制系统的测试性分析能力、诊断策略构建能力。

利用自行开发的仿真分析软件以某型惯性测量组合为对象，构建了9个模块共计29个故障模式的三层(分别为导航系统层、姿态测量分系统层、惯性测量组合单元1)基于故障扩散强度函数的多信号流模型。由于整个惯性测量组合故障模式多，建模分析过程复杂且内容过多，故以该惯性测量组合中二次电源、X轴陀螺仪、YZ轴陀螺仪、再放大器组合和A/D转换电路为例，研究故障在它们之间的传播关系，利用建模仿真软件建立的基于故障扩散强度函数多信号流模型如图7所示，通过建模仿真软件分析得到的故障传播关系如表3所示(继发故障是由相应的原始故障引起的，表3中故障编码对应的故障模式与表1一致)。

图7 某型惯性测量组合的基于故障扩散强度函数多信号流模型

表3 建模分析所得惯性测量组合中部分故障传播关系

由于二次电源故障模式较多，故以二次电源中的三相方波电源无输出故障为例进行详细分析说明：二次电源中的三相电源发生无输出故障，故障传播给X轴、YZ轴陀螺仪，使X轴、YZ轴陀螺仪分别发生X轴无输出、YZ轴无输出故障，然后再传播给陀螺再平衡放大器组合，使陀螺再平衡放大器组合发生信号放大器无输出故障，最后传播给A/D转换电路，使装备的运动姿态参数发生错误，即当二次电源发生三相方波电源无输出故障时，故障的传播路径如图8所示。

图8 三相方波电源无输出故障传播路径图

3 试验验证

在对该型惯性测量组合的故障传播进行建模仿真分析后将进行“故障注入-故障传播”试验，以验证建模仿真分析的故障传播结果的正确性，具体的试验对象如图9所示。

图9 某惯性测量组合内部的电路板

3.1 试验过程

考虑到故障注入的可行性和破坏性，实物试验共选取了表1中便于故障注入的7个无输出类的故障模式(分别为f1，f10，f12，f13，f16，f17，f18)和X轴陀螺仪X轴零位漂移故障(f11)共计8个故障模式，每个故障模式注入6次，得48个试验样本。其中无输出类故障的注入方法为断开输出端，X轴陀螺仪X轴零位漂移故障注入方法为软件故障注入模拟(解算程序中叠加一个0.01°零漂值)。

以该惯性测量组合中Y轴陀螺仪和二次电源两个位置的故障为例，对应的故障模式分别是Y轴无输出(故障模式编码为f12)和三相方波电源无输出(故障模式编码为f1)。试验过程中采用的故障注入方式分别为手动切断Y轴陀螺仪的信号输入和手动切断三相方波电源，该注入方式具有很好的可控性，能够准确控制故障注入到需要的地方。在准确进行故障注入后再通过万用表等仪器检测电路中各模块的信号(如图10所示)，通过信号的异常来判断故障的传播途径，得出试验得到的继发故障集，最后再将试验得到的继发故障集与建模分析得到的继发故障集进行比较以验证模型的准确性。对某型惯性测量组合中Y轴陀螺仪无输出和二次电源中三相方波电源无输出两种故障模式的故障进行传播验证的试验图如图10所示。

图10 某惯性测量组合故障传播试验图

3.2 试验结果

根据每次故障注入后对后续测试点进行测量，统计每次试验的后继故障集，试验所得后继故障集如表4所示。对试验数据进行统计分析知：无输出类故障的42个故障样本理论与试验结果完全一致，陀螺仪的X轴零位漂移故障的6个故障样本理论与试验结果不一致。

表4 惯性测量组合故障传播分析试验的故障注入样本表

对试验数据进行统计分析可知，无输出类的故障传播确定性较强，试验结果与理论分析一致，零位漂移类的故障存在一定的不确定性。

3.3 指标计算

依据48个模拟的故障检测结果数据，直接进行单点估计得到故障传播模型的准确率为：42/48=87.5%。

考虑到在样本选择和试验测试过程中存在一定的置信度，可以根据二项分布单侧置信下限估计方法计算故障传播模型的正确率指标(取置信度0.8)，准确率的计算式为

式中,n为样本量(48);F为检测失败次数(3);C为置信度(0.8);qL为解模糊能力指标的置信下限估计值。通过计算得到模型的准确率估计值为88.2%，造成该结果的原因可能是在理论建模时零位漂移类故障影响程度未考虑时间因素(陀螺仪零漂故障与时间的长短有关，未考虑故障演化)。

4 结束语

惯性测量组合是航空器中的核心部件，其工作精度高、功能结构复杂，易发生故障并在系统内传播，且其故障传播中存在两个难点：故障传播路径复杂多样性和故障传播存在不确定性，因此有必要针对这两个难点对惯性测量组合的故障传播机理进行研究分析。在对某型惯性测量组合故障传播路径的复杂多样性和故障传播不确定性进行研究的基础上，利用自行开发的建模仿真软件建立基于故障扩散强度函数的多信号流图模型，并通过试验验证了模型的准确性。研究表明，所构建的模型能够很好地解决惯性测量组合故障传播路径复杂多样性和传播不确定性的问题，为研究惯性测量组合故障传播机理奠定基础。

本文在理论建模时尚未考虑时间因素对故障传播的影响，而大量工程实践表明时间是影响故障传播的重要因素(例如，惯性测量组合中零位漂移类故障的影响程度就与时间长短密切相关)，因此，在下一步研究中还需考虑时间对故障传播的影响。