基于Bagging-CVA的动态过程及质量相关故障检测
郭小萍, 郭建斌, 高嘉俊, 李 元
(沈阳化工大学 信息工程学院,辽宁 沈阳 110142)
工业过程故障检测是保证产品质量和运行安全的关键。目前基于数据驱动的故障检测技术得到飞速发展[1-2],国内外已有许多研究成果,如基于主元分析(Principal Component Analysis,PCA)[3-4]、偏最小二乘(Partial Least Squares,PLS)[1,5]和典型变量分析(Canonical Variate Analysis,CVA)[6-7]等的故障检测方法。传统故障检测方法通常在检测出系统故障时发出报警,不显示该故障是否对质量产生影响的信息。随着现代生产过程对产品质量的要求不断提高,技术工程师和企业管理者更关心故障发生时,是否会影响到产品质量。目前对质量相关故障的检测方法的研究开始受到越来越多的关注[8-9]。过程发生故障时,根据故障是否影响最终产品质量,可以将故障进一步划分为质量相关故障和非质量相关故障[10]。
传统CVA方法可以提取过程变量与质量变量之间最大相关性,建立质量相关故障检测系统,监测质量相关故障对质量的影响。由于非质量相关故障对质量无影响,当生产过程发生此类故障时,质量相关故障检测系统不报警,从而发生漏报。Zhu等[11]通过PCA和CVA相结合的方法,能够对过程相关故障和质量相关故障同时进行监控。在生产过程中采集的数据通常具有时序相关性,该性质可能会对故障检测模型的精准度产生影响[12-13]。为了提高模型的性能,动态CVA(Dynamic CVA,DCVA)方法[14-15]采用Hankel增广矩阵构造动态相关矩阵进行建模,降低了数据时序相关性对模型的影响。但新构造的增广矩阵由于维度的扩展,增加了检测所需时间。基于滑动窗CVA(Moving Windows CVA,MWCVA)方法[16]通过滑动窗口构建动态相关矩阵。但如何选择最优窗宽参数是一个难题,窗宽太小会遗漏某些过程数据信息,降低检测性能,窗宽太大又会增加检测所需时间。Ge等[17]提出基于Bagging的SVDD(Support Vector Data Description)故障检测方法,首先使用Bagging随机抽样形成多组训练集,消除时序相关性,然后使用SVDD方法建立多个模型,采用贝叶斯方法对多个统计量进行融合。但该方法在故障检测时,需要计算多组模型的统计量并进行融合。
本文提出一种基于Bagging思想和典型变量分析(Bagging-Canonical Variate Analysis,Bagging-CVA)的动态过程及质量相关故障检测方法。针对时序相关性的问题,采用Bagging思想对建模数据进行随机抽样构成多组新的训练集,消除建模数据间的时序相关性;对每组新的训练集采用CVA方法分别建立过程故障检测模型和质量相关故障检测模型。基于多个模型对不同故障的检测率和误报率,提出了一种最优模型选取策略,对选出的检测率最高模型和误报率最低模型所对应的统计量进行融合,并作为最终故障检测统计量,减少故障检测采用多组模型结果进行融合的复杂度。在过程故障发生时,所提出的方法可以同时观察该故障是否影响产品质量。最后通过数值案例和TE过程仿真实验验证了所提方法的有效性,并与PCA、CVA和传统Bagging-CVA等方法进行了对比。
1 CVA原理
CVA的原理是在矩阵X=[x1,x2,…,xm]T∈Rm×p和Y=[y1,y2,…,ym]T∈Rm×q之间寻找最优投影方向a和b,使得投影后的典型变量l和w具有最大的相关性。其中m为样本数,p和q分别为矩阵X和Y的变量数。CVA的目标函数为
(1)
式中,ΣXX,ΣYY分别为X和Y的自协方差矩阵;ΣXY为X和Y之间的互协方差矩阵。上述优化问题可通过奇异值分解方法[7,14]实现:
(2)
式中,U和V分别为矩阵H的左右奇异矩阵;对角阵为D=diag{ρ1,ρ2,…,ρd},其对角线元素为典型变量间的相关系数,且ρ1≥…≥ρd,d=min{p,q}。投影矩阵A和B可以通过式(3)计算得出:
(3)
2 改进Bagging-CVA故障检测
2.1 CVA故障检测模型建立
采用CVA方法建立过程故障检测模型和质量相关故障检测模型。
(1) 过程故障检测模型。
使用过程数据集X,构造H矩阵并利用广义奇异值对其进行分解,计算公式为
(4)
根据式(3)计算得到最优投影矩阵Akx,其中Akx为矩阵A的前kx列,可以由典型变量间的相关系数累计贡献率[1,18]确定。确定过程相关的典型变量估计矩阵为
C=XAkx∈Rm×kx
(5)
(6)
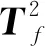
(2) 质量相关故障检测模型。
利用过程数据集X和质量数据集Y并根据式(3)进行CVA分析得到最优投影矩阵Aky。利用过程相关数据X构造质量相关的典型变量估计矩阵E和残差矩阵G:
E=XAky∈Rm×ky
(7)
(8)
矩阵E和G描述了过程变量和质量变量之间的信息,可以通过过程数据检测质量相关故障,构造相应的统计量[14]:
(9)
2.2 最优故障检测模型确定
过程数据通常具有很强的时序相关性,此类特性会对故障检测模型的精准度产生一定的影响。传统CVA方法通过采用增广矩阵的方式对过程数据进行预处理,可以降低过程数据时序相关性对故障检测模型性能的影响。然而,使用矩阵增广的数据处理方式,会产生一定的检测延迟。此外,使用增广后的数据矩阵进行典型变量分析可能会导致非正定矩阵的产生,对所建故障检测模型的性能产生巨大影响。针对上述问题,使用Bagging思想对过程数据进行预处理,消除过程数据的时序相关性。
Bagging算法[20-21]是一种集成算法,其基本原理是对原始数据集进行可重复抽样。每次从数据集中随机有放回地抽取一定数目的样本,这些样本组成一个新的训练集(称为一个袋),重复M次后,形成M组新的训练集。然后,使用M组新的训练集进行训练,并将最后的结果进行融合。在Bagging方法的基础上,提出一种最优模型选取方法,具体选取流程如图1所示。
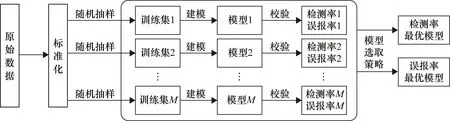
图1 基于Bagging算法思想的故障检测模型建立流程图
(1) 通过Bagging算法获得M组新的训练集,分别利用CVA方法建立M个过程相关故障检测模型和M个质量相关检测模型。
(2) 使用校验数据对这些模型进行校验,获得相应检测率和误报率。
(3) 通过设计一种模型选取策略确定最优模型,即设检验数据中有I类故障数据,应用所建立的M个检测模型中的每个模型会得到I个检测率和I个误报率,则可以构建一个检测率矩阵:
(10)
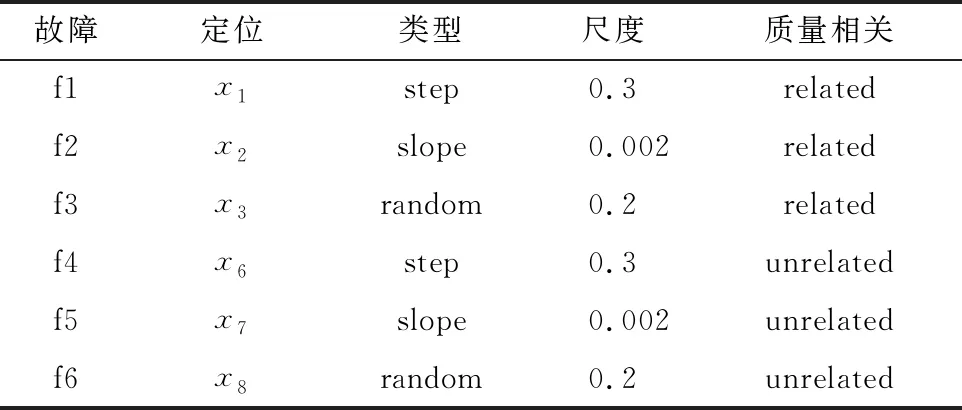
式中,fdrij为第i个模型的第j类故障数据的检测率。对检测率矩阵每列从大到小排序,计算前h行数值所对应的检测率矩阵索引i(h 当最高检测率模型和最低误报率模型确定后,对相应统计量通过贝叶斯融合策略进行融合[17]。 定义样本x在某一个模型中发生的概率为 (11) 式中,P(x|N)和P(x|F)分别为样本正常与故障的后验概率,计算公式如下: (12) (13) 式中,S为模型的统计量;S为控制限;P(F)为置信度α,则P(N)为1-α。融合后的统计量为 (14) 式中,融合后统计量BIC的控制限为置信度α;i为需要融合的模型个数,本文i值为2,即使用模型选取策略确定的最高检测率模型和最低误报率模型,减少了故障检测采用多组模型融合的复杂度。 该算法分为离线建模和故障检测两个部分,如图2所示。 图2 基于改进Bagging-CVA方法的过程及质量相关故障检测流程图 (1) 离线建模。 ① 将过程数据集X和质量数据集Y进行z-score标准化处理为Xnew和Ynew。 ② 对Xnew和Ynew同步随机抽样形成多组数据集,分别使用式(5)建立过程检测模型,使用式(7)和式(8)建立质量相关检测模型,并通过2.2节方法确定最优的过程故障检测模型和质量相关故障检测模型。 ④ 采用核密度估计法确定各统计量控制限,置信度设置为95%。 (2) 故障检测。 ① 采用离线数据对应的均值和方差对测试数据Xt进行标准化处理。 ③ 将各统计量分别按式(14)进行融合,其中使用离线过程的各最优模型统计量所对应的控制限。 ④ 判断融合后各统计量是否超限,故障是否发生。 参考文献[22]构造出一个具有动态过程和质量相关的仿真案例,其结构如下: (15) 其中过程数据X=[x1,x2,…,x10]T可以由X1=[x1,x2,…,x5]T和X2=[x6,x7,…,x10]T组成,x1~x5为质量相关的过程变量,x6~x10为非质量相关的过程变量。矩阵Y=[y1,y2,…,y5]T为质量数据集,y1~y5为质量变量。e~N(0,0.01)为高斯噪声,系数W1、W2和Z分别为 矩阵R=[r,2r+1,r2-1,r2-3r,-r3+3r2]T,则变量r的计算方法为 r(t)=0.811r(t-1)+0.193ω(t) (16) 式中,ω为随机变量,且ω~N(0,0.1)。 仿真实验时,通过式(15)获取样本长度为1000的正常数据作为训练集,并进行离线建模。再分别获取2组数据用于模型校验和故障检测,每组数据包均有6个数据集,在第501个采样点处引入故障,故障类型设置如表1所示。表中分别对不同故障的产生位置、发生方式、尺度以及是否与质量相关进行了设定。 表1 故障类型设置 图3和图4分别为故障1(质量相关故障)和故障6(非质量相关故障)的质量变量监视图。图3和图4均给出了质量变量y1~y5的波动情况,通过分析可知,在第500个采样点之后,质量相关的过程变量产生故障,质量变量波动情况异常。当非质量相关的过程变量产生故障时,质量变量则无明显波动情况。 图3 故障1的质量变量监视图 图4 故障6的质量变量监视图 图5 故障1的改进Bagging-CVA检测结果图 表2列出了6类故障检测结果,其中FDR为检测率(%),FAR为误报率(%),AVE为均值,主元个数均为3。与传统CVA方法进行对比(本文方法检测效果挺高部分已加粗显示),验证了本文所提出的方法的有效性。在此基础上,将所提出的方法应用于TE过程中,进一步验证其有效性。 表2 故障检测结果 TE过程已在故障检测领域广泛应用,详细介绍可见文献[23]。过程共有41个测量变量和12个控制变量。本文选择测量变量XMEAS(1~35)和控制变量XMV(1~11)作为过程变量,测量变量XMEAS(36~41)作为质量相关变量。TE过程共设有21种故障,故障均从第161采样时刻引入。使用本文方法对21种故障进行检测,其中本文参数选取为B=1000,α=0.025,各模型主元个数分别按照累计贡献率80%确定。对故障4(非质量相关故障)和故障7(质量相关故障)的检测结果进行了具体分析。其余故障均列表给出,并与PCA、 CVA和Bagging-CVA方法进行了对比。 图7 故障4的质量变量监视图 图8 故障4的改进Bagging-CVA检测结果图 通过工艺分析可知,故障7是组分C发生阶跃变化,导致系统质量相关变量波动异常,由于系统闭环调节作用,500时刻之后质量相关变量基本恢复正常。故障7的质量变量监视图如图9所示,在第161个采样点产生故障后,质量变量产生波动,第500个采样点后质量变量又逐渐恢复正常,其质量统计量T2在此采样点后也不再超限。 图9 故障7的质量变量监视图 图10 故障7的改进Bagging-CVA检测结果图 改进Bagging-CVA方法以及对比方法PCA、CVA和Bagging-CVA方法的过程相关故障检测结果如表3所示,详细列出各方法对不同类型故障的检测率和误报率。因故障3、9、15为较难检测故障,大多数基于数据驱动的方法检测效果不佳[24],本文不再列出。表中改进Bagging-CVA方法的检测效果提高部分已加粗显示。通过对比分析,本文方法的平均检测率和误报率指标均要优于其他方法。质量相关故障检测结果如表4所示,表4中给出了本文方法以及CVA和Bagging-CVA方法的数据对比。从表4中可以看出,改进Bagging-CVA方法的检测效果要优于其他方法,特别是误报率方面,几乎没有误报的发生。通过表3和表4的数据分析,进一步验证了本文方法的有效性。 表3 过程相关故障检测结果 表4 质量相关故障检测结果 本文提出一种动态过程及质量相关故障检测方法,采用Bagging算法思想可以消除样本间的时序相关性,并利用CVA方法分别建立过程相关故障检测模型和质量相关故障检测模型,在过程故障发生时可以进一步判断此类故障是否影响产品质量。提出的最优模型选取策略,可以在离线建模时直接确定最优故障检测模型,避免了传统Bagging算法对多组模型的检测结果进行融合的问题。通过仿真实验并与PCA、CVA和传统Bagging-CVA方法进行了对比,结果表明,在动态过程及质量相关故障检测方面,本文方法的检测能力均有一定程度的提高,验证了方法的有效性。此外,CVA方法是常用的线性算法,而现实过程中往往具有很强的非线性,如何处理此类问题将是下一阶段的研究重点。2.3 Bagging-CVA算法
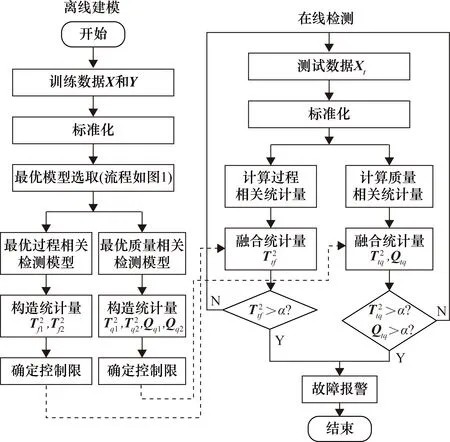
3 仿真研究
3.1 数值案例

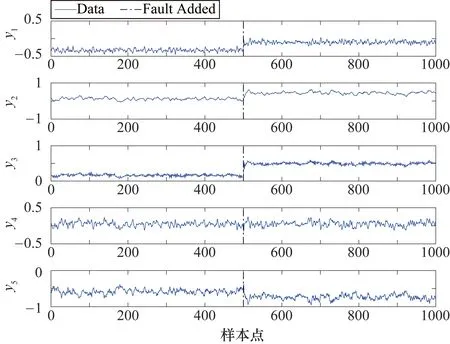
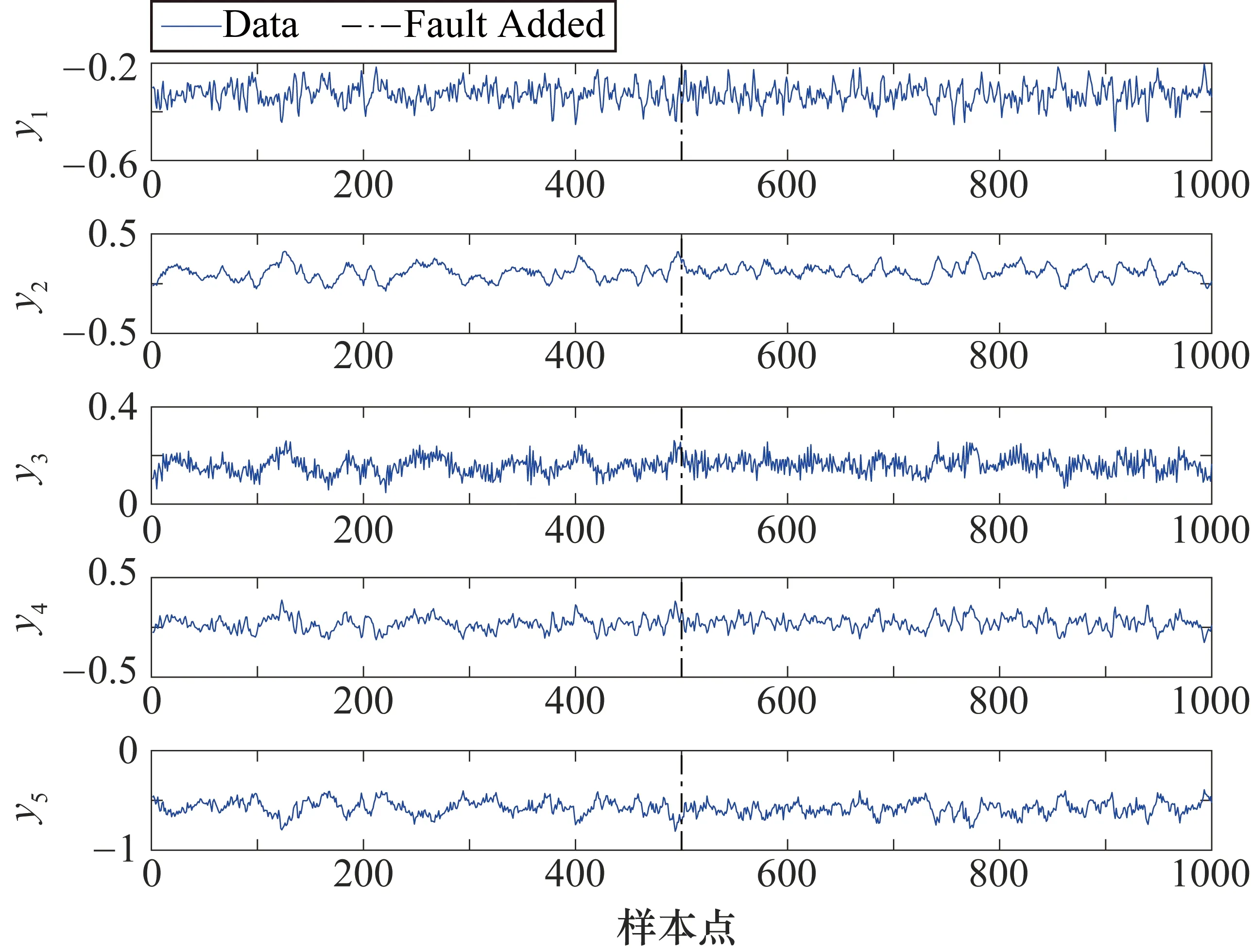
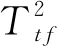


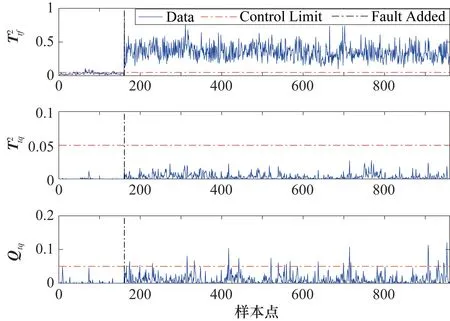
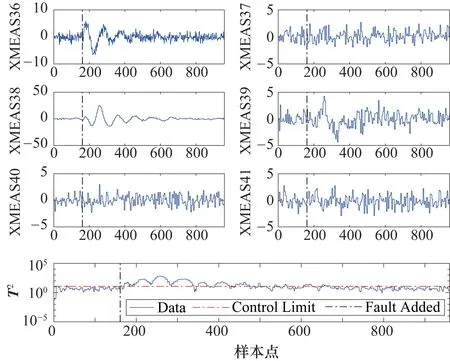
3.2 TE过程
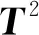

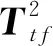
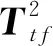
4 结束语

