藏族小学数困生应用题表征特点研究——以藏族四年级学生为例

巴桑卓玛，史宁中，覃若男，李 婷

藏族小学数困生应用题表征特点研究——以藏族四年级学生为例

巴桑卓玛1，2，史宁中2，覃若男1，李 婷1

（1．西藏大学 理学院，西藏 拉萨 850000；2．东北师范大学 数学与统计学院，吉林 长春 130024）

以小学四年级藏族学生为被试，探讨藏族数学学习困难学生的问题表征．从拉萨市某普通小学的藏族班中选取60名学生，自编4种不同类型的典型应用题，采用数学测试和口头报告法进行研究．研究结果发现：（1）在解决4类应用题时，藏族数优生使用的表征类型多样且灵活，而两类藏族数困生的表征类型偏单一性且效能水平低．（2）在解决4类应用题时，两类藏族数困生使用关系表征的人数显著低于藏族数优生，两类藏族数困生之间无显著差异．（3）3类藏族学生倾向于使用复述表征，两类藏族数困生使用复述表征的人数显著多于藏族数优生；两类藏族数困生倾向使用复述表征、图像表征、直译表征，对关系表征、图示表征使用的频次相对较低．（4）3类藏族学生解题成绩与表征种数、关系表征呈非常显著正相关，与复述表征、图像表征呈显著负相关．

藏族小学；数困生；应用题；问题表征

1 问题提出

数学学习困难（mathematics learning disability，MD）在数学学习中是跨地区、跨文化的存在，是数学教育中共有的难题．共同认可的数学学习困难发生率在6%~7%，但对于西藏地区来说，结合历年西藏地区的高考成绩可以推测数学学习困难的发生率会较高，因为少数民族地区的数学学习中存在跨文化数学教育的难度和阅读困难（reading disability，RD）等问题．在多项研究中证明数学应用题解决（mathematical word problem solving）是数学困难儿童的一致障碍[1]．

问题表征是一种反映问题加工的过程，是解决问题的核心环节[2]．关注题目中不同信息的学生解题正确率不同，即表征类型将影响应用题的成功解决[3]，因此问题表征的能力、质量和方式将直接影响到数学应用题的解决[4]．在解决问题的过程中通常从试图理解问题的基本结构开始，然后构造某种类型的问题表征以确定解决方案，因为构造表征的过程逐渐形成求解过程，除非有一个合适的表征，否则很难解决一个问题[5]．陈英和、仲宁宁等研究二~四年级儿童解答一致和不一致应用题的表征得出学生在数学问题解决中的困难在于其问题表征上，而不在数学操作上[6]，但是数学困难儿童的表征类型通常属于不适宜表征，不利于问题解决[7]．研究者基于前人对儿童问题表征类型的不同划分，并综合以往研究结果，将问题表征类型划分为5类：复述表征、图像表征、图式表征、直译表征、关系表征[8]．

目前，国内对数学学习困难儿童的问题表征研究集中于汉族学生或内地学生，相对民族地区这一问题关注相对较少．藏族小学生数学平均分普遍低于国内其他地区，而四年级是儿童问题表征发展中的一个关键期与转折期[9]．因此以藏族四年级小学生为研究对象，讨论藏族小学数学学习困难学生应用题表征的特点．

2 研究方法

2.1 被试

选取的被试为拉萨市某小学四年级藏族学生．根据任课教师的评价和瑞文智力测试，剔除智力水平测试成绩异常者，按照最近一次数学考试成绩和语文考试成绩进行筛选，共筛选60人，数学学习优秀组、单纯型数学学习困难组（只患有MD）、混合型数学学习困难组（患有MD+RD）各20人（平均年龄10.32±0.21）．根据成绩—智力差异法进行筛选，数学学习优秀组（简称数优生）被试选取的标准为：期中、期末统一考试中数学、语文成绩位于全年级的前25%，且任课教师评定为数学、语文成绩优秀的学生；单纯型数学学习困难（简称单困生）被试的选取标准为：期中、期末数学统一考试的成绩位于全年级的后25%，且期中、期末语文统一考试的成绩位于全年级前70%，同时由任课教师评定为数学成绩较差，语文学习正常的学生，无其它缺陷、障碍和疾病；混合型数学学习困难（简称双困生）被试的选取标准为：期中、期末考试中数学考试成绩和语文考试成绩均位于全年级的后25%，且任课教师评定为数学、语文学习情况差的学生，无其它缺陷、障碍和疾病．

2.2 研究材料

（1）应用题测试卷根据义务教育阶段课程标准和人教版四年级数学教材的课后习题自编28道应用题，共4种类型，分别是比较问题、倍数问题、列队问题、路程问题．随机选取一个四年级班级进行预测，结合预测结果和西藏小学一线教师的建议，最终选择平均难度在0.613的8道题作为正式测试材料，每种类型应用题各2道，将8道题进行拉丁方排列后施测．每道题后均设置五选一的表征方式选择题（复述表征、图像表征、图式表征、直译表征、关系表征）．

（2）笔、记录纸、录音笔．

2.3 研究假设

假设1：3类藏族学生表征类型的种数及应用频次存在差异．假设2：在不同类型应用题上3类藏族学生的表征类型存在显著差异．假设3：3类藏族学生解决应用题时选择的表征类型、表征种数对学生的解题成绩产生显著影响．

2.4 实验过程

（1）实验前对被试集中进行应用题表征的口语报告训练，确保被试理解5种表征，能顺利进行口语报告．在安静的教室里采用自编测试题正式施测，要求被试按顺序答题，完成一道题后用录音笔记录其口语报告，整个测试时间为40分钟．

（2）正确解答每道题记1分，错误回答记0分．将8道题的得分相加作为解题成绩；对被试的口头报告和测试卷进行分析，统计被试在每道应用题上的表征类型．

3 结果分析

3.1 3类学生表征类型的种数及应用频次比较

3类学生复述表征的频次最高，且图式表征的频次明显低于其它表征类型．由表1可知，3类学生表征类型的种数有显著差异（(2, 57)=17.884，＜0.05），根据LSD事后检验分析发现，在表征类型的种数上，数优生显著高于两类数困生，且两类数困生之间无显著差异．

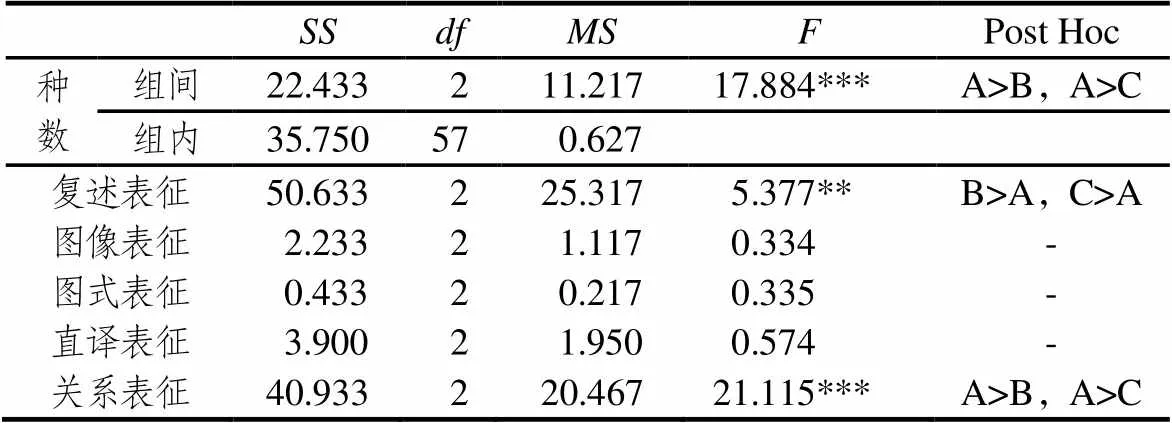
表1 3类学生使用表征类型的种数及频次的方差分析

注：A为数优生，B为单困生，C为双困生；*<0.05，**<0.01，***<0.001，下同．

3类学生使用5种表征类型在频次上存在显著差异（Wilk’s Lambda=0.017，=766.213，<0.05），两类数困生在复述表征上的频次显著高于数优生，两类数困生之间无显著差异；3类学生在图像表征、图式表征、直译表征的频次上无显著差异；数优生对关系表征的使用频次显著高于两类数困生，两类数困生之间无显著差异．

3.2 在不同类型应用题上3类学生的表征类型比较

3.2.1 不同类型应用题上3类学生的表征倾向分析

将3类学生在4类应用题上对5种表征类型的选择率进行卡方检验，结果表明：3类学生在解决4类应用题时，使用5种表征类型人数上有显著差异．进一步分析发现，3类学生在解决比较问题、倍数问题时，使用复述表征的人数显著高于其它表征；3类学生在解决列队问题中，使用复述表征、图像表征的人数显著高于图式表征、直译表征、关系表征；在解决路程问题中，关系表征的使用人数显著低于其它表征．复述表征在4类题目中的使用频次最高，图式表征在4类题目中的使用频次最低．具体见表2．

表2 不同类型应用题中使用各种表征的差异分析

3.2.2 3类学生在解决比较问题上的表征类型比较

对3类学生在比较问题上使用5种表征的人数进行方差分析，结果表明：3类学生在解决比较问题时，使用5种表征类型的人数有显著差异（Wilk’s Lambda=0.067，= 189.471，<0.05）．3类学生在比较问题上使用关系表征的人数存在非常显著的差异，数优生使用关系表征的人数显著多于两类数困生，而两类数困生之间无显著差异．数优生和双困生在复述表征上存在显著差异，双困生使用复述表征的人数明显高于数优生．具体见表3．

表3 解决比较问题上使用各种表征人数的方差分析

3.2.3 3类学生在解决倍数问题上的表征类型比较

在解决倍数问题时，两类数困生倾向于使用复述表征，使用图式表征的人数最少．对3类学生在倍数问题上使用5种表征的人数进行方差分析，结果表明：3类学生使用5种表征方式的人数存在显著差异（Wilk’s Lambda=0.051，=249.072，<0.05）．3类学生使用复述表征、图像表征、图式表征、直译表征解决倍数问题上无显著差异．数优生使用关系表征的人数显著高于两类数困生，两类数困生之间没有显著差异．具体见表4．

表4 解决倍数问题上使用各种表征人数的方差分析

3.2.4 3类学生在解决列队问题上的表征类型比较

在解决列队问题时，两类数困生都倾向于使用图像表征、复述表征，双困生没有使用关系表征和图式表征，单困生没有使用关系表征．进一步对3类学生在列队问题上使用5种表征的人数进行方差分析，结果表明3类学生使用5种表征的人数存在显著差异（Wilk’s Lambda=0.004，=285.721，<0.05）．分析发现3类学生只在图式表征、关系表征上存在显著差异：数优生使用图式表征、关系表征的人数显著高于两类数困生．具体见表5．

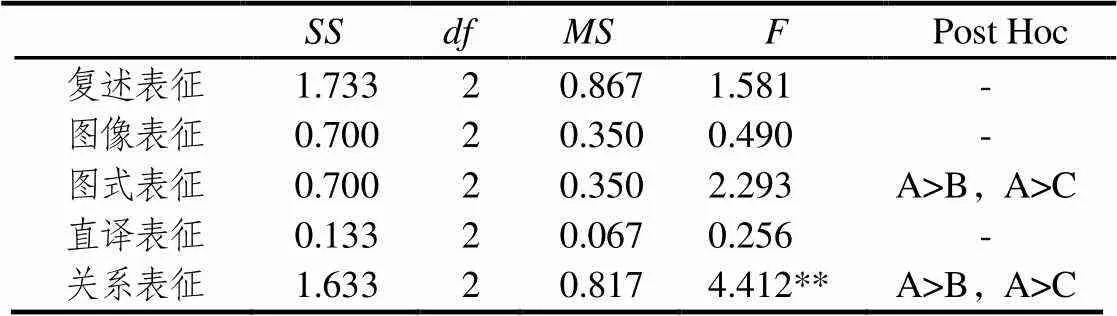
表5 解决列队问题上使用各种表征人数的方差分析

3.2.5 3类学生在解决路程问题上的表征类型比较

在解决列队问题时，数优生倾向于使用直译表征、关系表征，两类数困生倾向于使用复述表征、图像表征，双困生未使用图式表征和关系表征．进一步对3类学生在路程问题上使用5种表征的人数进行方差分析，结果表明：3类学生使用5种表征的人数存在显著差异（Wilk’s Lambda=0.057，=224.838，<0.05）．3类学生使用关系表征、复述表征上存在显著差异，两类数困生之间没有显著差异．数优生使用关系表征的人数显著高于两类数困生，而两类数困生使用复述表征的人数显著高于数优生．具体见表6．

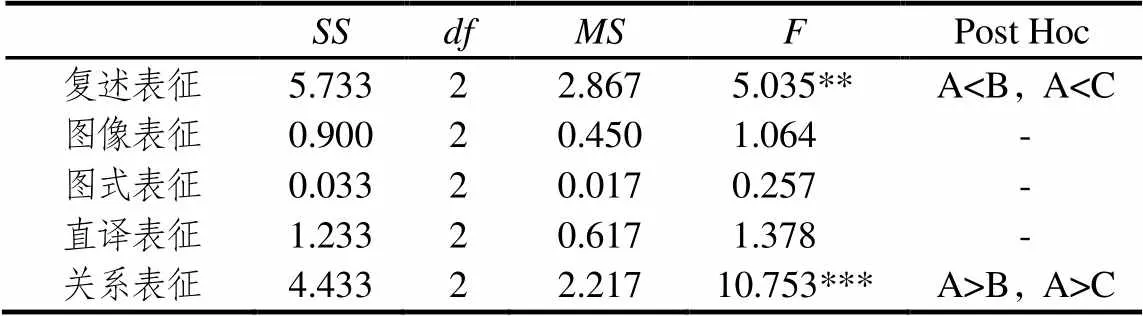
表6 解决路程问题上使用各种表征人数的方差分析

3.3 3类学生解题成绩与表征种数及表征类型频次的关系

3类学生在解题成绩上存在非常显著的差异（(2, 57)= 87.497，<0.001），事后检验结果表明：数优生的成绩显著高于两类数困生，双困生的解题成绩显著低于单困生．由表7可知，3类学生解题成绩与表征种数、关系表征频次呈非常显著正相关（<0.01），与复述表征频次、图像表征频次呈显著负相关（<0.05），与图示表征频次、直译表征频次未达到显著的相关水平．表征种数与关系表征频次、图式表征频次呈显著正相关，与复述表征频次呈非常显著负相关，与图像表征频次、直译表征频次未达到显著相关水平．

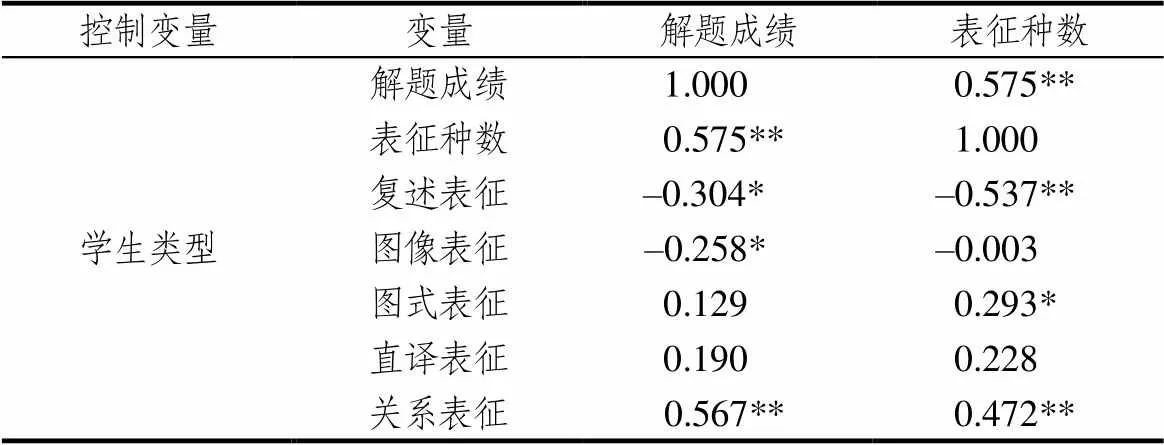
表7 3类学生解题成绩与表征种数及各表征频次相关分析

4 讨论

4.1 3类学生应用题表征类型的差异分析

在考查3类学生解决4类应用题时的表征种数差异时，发现数优生偏向于使用3种及3种以上的表征类型，而两类数困生表征类型呈单一性并且多使用复述表征、直译表征、图像表征，这表明学生类型的差异直接体现在藏族小学生问题表征种数以及表征水平上．这主要是由于数困生对问题本质特征的概括能力及分析比较能力相对较弱，因此在解决不同类型应用题上不能灵活地选择、变换表征类型[7]．两类数困生不仅对问题的分析能力较弱，而且其掌握的表征方式也存在问题，在面对不同问题时，两类数困生掌握的表征种数不足以进行灵活转换，而数优生能够根据不同问题类型、难度选择合适的表征．这也可能与数困儿童的工作记忆容量存在关系[10]，因为直译表征、图像表征等对题目的加工相对简单，从而工作记忆的负荷小．对3类学生5种表征的使用频次分析也证实了这一点：两类数困生解题时倾向于使用效能水平较低的表征（复述表征、直译表征、图像表征）．综合以往研究结果，中国差生会经常采用复述表征[11]．Mayer、Hegarty提出在解决一致/不一致问题时，不成功解题者使用直译表征：只关注题目中的数字或关系词语，而无法利用问题模型表征对题目内在关系建构问题情境[12]，并且国内在Hegarty的研究基础上进行了大量的研究，研究结果与其一致．认知机制和认知能力也是制约3类学生应用题表征的因素．李清的研究发现PASS各认知过程对小学数学双困生、单困生和学优生的应用题成绩、表征水平具有显著预测作用[9]．综上，3类学生对复述表征、图像表征的使用频次高，藏族学生的数学应用题表征水平整体较低．在双语教学中，平衡的双语能力是少数民族双语教学的前提条件，学生的双语言能力与认知能力在发展过程中相互影响、相互促进[13–15]．Cummins的母语与目的语相互依存假说认为双语学生的第二语言能力依存于已经获得的第一语言能力，第一语言越发达，第二语言的习得越容易，平衡的双语者在认知发展上具有认知优势[16]．只有学生的语言能力得到足够的发展，才能促进整个认知系统的发展．因此，在藏汉双语数学教学中，教师注重训练数困生对应用题的概括能力和分析能力，针对不同类型的应用题进行系统的表征训练，从掌握表征方式开始，在解题中练习运用；其次，少数民族地区的数学教师必须具备双语教学能力，能够用藏、汉双语对数学知识进行融合贯通，减少记忆数学知识的负担；最后，教师不能把双语教学的认识归于仅仅是学习第二语言，忽视母语与第二语言的依存关系，学生无法正常地接受并掌握数学知识，对数学知识产生畏惧心理，对数学失去兴趣，数学教学很难取得预期的效果．

4.2 不同类型应用题对3类学生表征方式的影响

在解决比较问题和倍数问题时，数优生倾向于使用关系表征，与之前的研究结果一致，但同时倾向于使用复述表征，语言可能是导致数优生在解决数学应用题中较多使用复述表征的因素．因为这类数学应用题语义相对比较复杂，需要对题目进行更多的认知加工，而藏族学生首先需要将汉语的数学题目读懂，理解文字层面的意思，其次需要用数学的逻辑对题目进行理解．研究表明，民族地区学生数学成绩受语言影响[17]，双语儿童在阅读时会受到母语的语言结构、语法规则和用词习惯的干扰，并且习惯于用民族语言进行思维[18]，两种语言的思维转换上存在困难，这就导致在解题过程中，出现关系表征的同时伴随着复述表征．根据数优生的解题成绩判断复述表征的使用与其学习能力无关．两类数困生倾向于使用复述表征和图像表征，与之前的研究结果一致．数困生在使用其它表征类型时同样伴随着复述表征，但是数困生则存在语言和学习能力的双重影响．因此，语文能力的高低直接影响藏族小学生数学应用题问题表征水平，需要处理好小学低年级阶段语文教学和数学教学之间相互衔接问题，着重加强数学语言的辅助训练，训练学生理清数学语言之间的逻辑关系，将应用题中的数学条件进行拆解，就像找语文句子的“主语”“谓语”“宾语”等句子成分一样，找出数学题目中的“已知条件”“变化量”“所求问题”等应用题成分，理解每一个数学条件与应用题之间的关系；也可以进行逆向思维训练：同时给出多个数学条件，要求学生进行合理组合并进行解答．

在解决视空特征明显的列队问题、路程问题时，图式表征通常是解决问题的捷径，3类学生在解决不同类型应用题上都不擅于使用图式表征，多使用的是图像表征，而建构一个恰当的问题表征是解决数学问题的关键环节，正确的表征是解决问题的必要前提，在错误的或者不完整的问题空间中进行搜索，不可能求得问题的正确解决[19]．宋广文等人研究发现视觉—空间工作记忆对解决不同难度应用题都存在影响，并且对应用题的表征方式存在影响[4]．3类学生的应用题解题成绩与图像表征频次呈负相关，说明使用图像表征不利于成功解题．3类学生的空间可视化能力弱，使用图式表征水平较低，因为低空间可视化能力的学生表现出偏好使用图像，也就是不太复杂的图像类型，具有高空间可视化能力的学生更倾向于使用图式，即蕴含更复杂关系的图像类型[20]．在空间任务上表现更好的人在数学能力测试上也表现更好[21]．在部分整体推理任务上进行的空间可视化也与孩子在二、五、六和七年级的爱荷华州基本技能测验的数学子测验中的表现显著相关[22]．因此，教师在讲解视空特征较明显的应用题时，应该引导学生使用图式表征策略，帮助藏族学生逐步构建和使用图式表征．

4.3 表征种数及不同表征方式对解题成绩的影响

3类学生掌握的表征种数及在不同题型中对表征方式的灵活运用直接影响解题成绩，使用关系表征的次数越多，解题的正确率越高；使用复述表征、图像表征的次数越多，解题正确率越低．这充分说明关系表征在解题过程中是有效的表征方式，而复述表征、图像表征会对学生的解题成绩产生负影响[23]．数优生使用关系表征的次数显著高于两类数困生，两类数困生不能理解数学应用题所隐含的内在逻辑关系，只做浅显的数量运算，因此双困生使用了复述表征来解决不同类型的问题．3类学生关系表征的选择率低，但是正确率高，表明关系表征是一种强势表征，学生使用关系表征找出题目中的重要关系词、变量名和数字之间的关系，能够建立起正确的问题模型，所以解题成绩与关系表征呈现出强正相关．辛自强采用微观发生法，从路线、速度及来源探究儿童表征深度的变化，发现练习、自我解释及混合练习模式对儿童的表征深度具有促进作用[24]．因此，在数学课堂教学中，对藏族小学生关系表征的使用进行有目的训练，有助于提高藏族小学生的应用题表征能力．

5 结论与展望

5.1 结论

（1）在解决4类应用题时，数优生使用的表征类型多样且灵活，而两类数困生的表征类型偏单一性且效能水平低．

（2）在解决4类应用题时，两类数困生使用关系表征的人数显著低于数优生，两类数困生之间无显著差异．

（3）3类学生倾向于使用复述表征，两类数困生使用复述表征的人数显著多于数优生；两类数困生倾向使用复述表征、图像表征、直译表征，对关系表征、图示表征使用的频次相对较低．

（4）3类学生解题成绩与表征种数、关系表征呈非常显著正相关，与复述表征、图像表征呈显著负相关．

5.2 研究展望

目前，少数民族数学教育研究正处于发展期，越来越多的学者致力于研究民族地区的数学教育[25–29]．应用题是数学教育中的重点，也是难点，对题目语义的正确理解是成功解题的首要条件，可以说语言是影响少数民族学生数学学习的重要因素．目前，西藏地区主要采用两种藏汉双语教学模式：第一种，以藏语授课为主，同时开设汉语课，简称为“藏+汉”，在农牧区小学、教学点和部分初中采用此类模式进行教学，高中基本不采用此类模式；第二种，以汉语授课为主，藏语作为少数民族学生必修课，简称为“汉+藏”，大部分小学、部分初中、高中学校以及西藏班采用此类模式进行教学．西藏双语教学具有两个最明显的特征：一是课程的设置已经具备了双语教育的要求；二是教学体系中，教学用语的布局严重失衡，没有形成平衡的藏、汉双语教学体系．因此，后续研究应该从双语学习与认知发展的关系理论出发，探讨双语学习与藏族学生数学认知发展的关系，探究其背后的原因及影响因素，以解决西藏地区数学教育相对落后的现实，提高西藏地区数学双语教学质量．

[1] ANDERSSON U. Mathematical competencies in children with different types of learning difficulties [J]. Journal of Educational Psychology, 2008, 100 (1): 48–66.

[2] SIMON H A, DANTZIG G B, HOGARTH R. Decision making and problem solving [J]. Interfaces, 1987, 17 (5): 11–31.

[3] HEGARTY M, KOZHEVNIKOV M. Types of visual–spatial representations and mathematical problem solving [J]. Journal of Educational Psychology, 1999, 91 (4): 684–689.

[4] 宋广文，何文广，孔伟．问题表征、工作记忆对小学生数学问题解决的影响[J]．心理学报，2011，43（11）：1 283–1 292．

[5] NOVICK L R, HMELO C E. Transferring symbolic representations across nonisomorphic problems [J]. Journal of Experimental Psychology: Learning, Memory and Cognition, 1994, 20 (6): 1 296–1 321.

[6] 陈英和，仲宁宁，赵宏，等．小学二~四年级儿童数学应用题表征策略对其解决不规则问题影响的研究[J]．心理科学，2005，28（6）：36–39．

[7] 郑琳娜，张奇．数学困难儿童的表征类型及其对应用题解决的影响[J]．中国健康心理学杂志，2007（6）：521–523．

[8] 郑琳娜．小学生数学应用题表征类型对问题解决影响的实验研究[D]．大连：辽宁师范大学，2007：22–23．

[9] 李清，王晓辰．小学数困生应用题列式成绩、表征水平与PASS各认知过程的关系[J]．心理科学，2010，33（5）：1 234–1 236，1 261.

[10] 胥兴春，刘电芝．数学学习障碍儿童问题解决的表征研究[J]．心理科学，2005，28（1）：186–188．

[11] 张庆林，管鹏．小学生表征应用题的元认知分析[J]．心理发展与教育，1997，13（3）：11–14．

[12] HEGARTY M, MAYER R E, MONK C A. Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers [J]. Journal of Educational Psychology, 1995, 87 (1): 18–32.

[13] 尚紫薇．21世纪初越南少数民族双语教育发展及特色探析[J]．民族教育研究，2013，24（1）：94–98．

[14] 张京花，李英浩．双语教育的国际视野及对中国少数民族双语教育的启示[J]．民族高等教育研究，2013，1（5）：60–63．

[15] 才让措，普华才让，尖措吉，等．藏汉双语能力发展的生态化分析——基于青海藏族学生藏汉双语能力发展测验[J]．中国藏学，2013（2）：25–29．

[16] CUMMINS J. Empirical and theoretical understandings of bilingual education [J]. Journal of Education, 1981, 163 (1): 16–29．

[17] 钟志勇．民族地区初中生数学学业成绩与语言关系的实证研究——以蒙古族学生为例[J]．民族教育研究，2013，24（4）：80–84．

[18] 万明钢，邢强．双语教学模式与藏族学生智力、学业成绩关系研究[J]．西北师大学报（社会科学版），1999（5）：76–81．

[19] 傅小兰，何海东．问题表征过程的一项研究[J]．心理学报，1995（2）：204–210．

[20] 柳笛．不同亚型数学学习困难儿童应用题问题表征过程的研究[J]．心理与行为研究，2018，16（4）：497–504．

[21] DELGADO A R, PRIETO G. Cognitive mediators and sex-related differences in mathematics [J]. Intelligence, 2004, 32 (1): 25–32.

[22] GUAY R B, MCDANIEL E D. The relationship between mathematics achievement and spatial abilities among elementary school children [J]. Journal for Research in Mathematics Education, 1977, 8 (3): 211.

[23] 董妍，路海东，俞国良．小学生应用题表征的类型和特点[J]．心理科学，2004，27（6）：1 352–1 355．

[24] 张睆，辛自强．儿童表征深度的微观变化：路线、速度及来源[J]．心理发展与教育，2015，31（2）：137–148．

[25] 唐瑜君，张萍．中国少数民族数学教育研究热点及发展趋势——基于2019年全国少数民族数学教育研讨会[J]．数学教育学报，2019，28（6）：95–97．

[26] 陈婷，徐冉冉．中国少数民族数学教育的“现状”“问题”及“对策”——2017年全国少数民族数学教育研讨会暨西藏数学教学改革研讨会会议纪要[J]．数学教育学报，2018，27（1）：96–98．

[27] 万明钢，海路．新中国成立70年少数民族教育发展的回顾、反思与展望——万明钢教授专访[J]．民族教育研究，2019（4）：7–12．

[28] 贾旭杰，何伟，孙晓天，等．义务教育阶段国家数学课程标准在我国民族地区的适应性研究[J]．民族教育研究，2019（4）：32–39．

[29] 苏德，张良，江涛．新时代背景下的少数民族双语教育：机遇·挑战·策略[J]．民族教育研究，2019（4）：71–76．

A Study of the Solution Representations of the Fourth Grade Tibetan Students with Mathematics Learning Disability on Word Problem Solving

BA Sangzhuoma1, 2, SHI Ning-zhong2, QIN Ruo-nan1, LI Ting1

(1. College of Science, Tibet University, Xizang Lasa 850000, China;2. School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China)

This study explored the solution representations of 60 Fourth-Grade Tibetan students with Mathematics Learning Disability in solving four types of problems. The results indicate that (1) the representations of excellent students in solving problems were diverse and flexible, and the types of problem representations of children with MD/MD+RD were stereotyped and low level; (2) when solving different word problems, the number of students with MD/MD+RD using relational representation was significantly lower than that of excellent students, and there was no significant difference between students with MD and students with MD+RD; (3) three types of Tibetan students tended to use the rehearsal representation, with the number of students with MD/MD+RD using the rehearsal representation significantly higher than the number of excellent students doing so and students with MD/MD+RD tending to use the rehearsal representation, picture representation, and direct translation whereas the frequencies of relational representation and schematic representations were relatively low; and (4) the problem-solving scores of three types of Tibetan students were positively correlated with the number of representations and relation representation but negatively correlated with rehearsal representation and picture representation.

Tibetan elementary school; mathematics learning difficulties; word problems; solution representations

附录：应用题测试卷

1. 小玉和小明在同一天过生日，已知小玉今年10岁，比小明大2岁，问小明今年多少岁？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出代表小玉、小明年龄的线段图，然后列式．

C 先在脑中想象有两个人，再想象小玉、小明各多少岁，或者想象得更为详细，然后列式．

D 找出题目中的数字“10”“2”，或者看关键词语“大”，然后列式．

E 分析各个句子表达的意思，然后明确小明与小玉年龄之间的数量关系，再列式．

2. 小明有一根长25米的绳子，第一周剪去2米，第二周剪去的长度比第一周的2倍少1米，请问这根绳子还剩下多少米？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出绳子原长度与两次被剪去长度的线段图，然后列式．

C 先在脑中想象有一根25米长的绳子，根据题目想象每次剪去多少米，剩下多少米，然后列式．

D 找出题目中的数字“25”“2”，或者看关键词语“剪去”“比……2倍少1米”，然后列式．

E 分析各个句子表达的意思,明确绳子长度与剪去长度之间的关系，再明确第一周剪去的长度与第二周剪去的长度之间的数量关系，得出第二周剪去的长度，再列式．

3. 一个方队，共8列，小明在第3列，小明前面有3个人，后面有5个人，这个方队共有多少人？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出代表方队的简单图案，然后列式．

C 先在脑中想象8列纵队,再想象小明的位置，或者想象的更为详细，再列式．

D 找出题目中的数字“8”“3”“5”，或者其它关键词语，然后列式．

E 分析各个句子表达的意思，然后明确小明前后的人数与方队每列人数之间的关系，再列式．

4. 一辆汽车从甲地到乙地，3小时行驶了192千米，还要再行驶2个小时才能到达乙地，问甲乙两地相距多少千米？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出甲乙两地距离、汽车已经行驶的路程、未行驶路程的线段图，然后列式．

C 先在脑中想象甲乙两地，再想象汽车已经行驶的路程，或者想象的更为详细，再列式．

D 找出题目中的数字“3”“192”“2”，或者其它关键词语，然后列式．

E 分析各个句子表达的意思，然后明确汽车“3小时行驶192千米”（求得汽车速度）与“再行驶2小时到达乙地”的关系，再列式．

5. 小明和小强看同一本书，小明每天看10页，比小强多看2页，请问小强每天看几页？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出代表两者数量关系的线段图，然后列式．

C 先在脑中想象有一本书，再想象小明每天看多少页，小强看多少页，然后列式．

D 找出题目中的数字“10”“2”，或者看关键词语“多”，然后选择列式的方法．

E 分析各个句子表达的意思，然后明确两个人看书页数之间的数量关系，再列式．

6. 小明有一根长60米的绳子，第一次剪去4米，第二次剪去的长度是第一次的3倍，请问这根绳子一共剪了多少米？这根绳子还剩下多少米？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出绳子原长度与两次被剪去长度的线段图，然后列式．

C 先在脑中想象有一根绳子，再想象每次剪去多少米，剩下多少米．或者想象得更为详细，然后列式．

D 找出题目中的数字“60”“4”“3”，或者看关键词语“剪去”“是……的3倍”，然后列式．

E 分析各个句子表达的意思，明确绳子长度与剪去长度之间的关系，再明确第一次剪去的长度与第二次剪去的长度之间的数量关系，得出第二次剪去的长度，再列式．

7. 一个方队，共4列，小明在第2列，小明站在最后面，小明的前面有2个人，求这个方队每列多少人？这个方队共有多少人？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出代表方队的简单图案，然后列式．

C 先在脑中想象4列纵队，再想象小明所站的位置，或者想象的更为详细，再列式．

D 找出题目中的数字“4”“2”，或者其它关键词语，然后选择列式的方法．

E 分析各个句子表达的意思，然后明确小明前面的人数与方队每列人数之间的关系，再列式．

8. 新星小学与少年宫相距1 400米，王军要从学校走到少年宫，每分钟走55米，走了12分钟后，请问王军走了多少米？他距少年宫还有多少米？

请列式并计算：

请选择你所采用的理解题意的方法：（）

A 多读几遍题目，再列式．

B 在纸上画出或在心里想出代表新星小学与少年宫两地距离的线段和王军12分钟所走路程的线段，然后列式．

C 先在脑中想象学校和少年宫，再想象王军行走的路程，或者想象的更为详细，再列式．

D 找出题目中的数字“1 400”“55”“12”，或者其它关键词语，然后选择列式的方法．

E 分析各个句子表达的意思，然后明确王军12分钟走了多远，王军已走的路程与他与少年宫之间的距离之间的数量关系，再列式．

G752

A

1004–9894（2021）01–0097–06

巴桑卓玛，史宁中，覃若男，等．藏族小学数困生应用题表征特点研究——以藏族四年级学生为例[J]．数学教育学报，2021，30（1）：97-102．

2020–09–30

国家自然科学基金项目——西藏地区藏汉双语数学教学中的语言问题研究（11926413）；中国博士后基金项目——1-3年级藏族学生数学语言学习的研究（2014M560226）

巴桑卓玛（1973—），女，藏族，西藏日喀则人，教授，博士后，硕士生导师，主要从事数学课程与教学论研究．

[责任编校：周学智、陈隽]