深度学习的内涵与教学实践——以小学数学为例

于 然，赵世恩

深度学习的内涵与教学实践——以小学数学为例

于 然1，赵世恩2

（1．河北科技师范学院 数学与信息科技学院，河北 秦皇岛 066004；2．首都师范大学 初等教育学院，北京 100048）

计算机科学中的深度学习与教育学中的深度学习在理论方面有着很大的区别，但它们实现的过程却有着密切的联系，这是因为计算机科学中的深度学习本质上就是模拟人脑认识世界的一种算法．首先，明确了教育学中深度学习的内涵，讨论两个领域中深度学习的关系；其次，在分析计算机科学中深度学习实现过程的基础上，具体解释了基于深度学习的教学实践若干关键步骤；最后，研究了一个课例——“位置与方向”，给出了基于深度学习的教学过程．

深度学习；小学数学；教学实践

近年来，诸多学者对数学教育的实践性问题进行了深入研究．如：郑毓信从教师的角度探讨数学教育的实践性问题，研究了教师专业成长的主要特征[1]；毕渔民在相关文献研究的基础上，探索了五环综合数学活动教学的教学形式[2]；温建红等学者专门研究了教学课堂预设提问的策略，讨论了教学问题提出和数学活动经验的关系[3–6]．随着研究的不断深入，深度学习在教育领域的研究引起了教育工作者的高度重视，而如何促进深度学习的发展，如何培养学习者的深度学习能力以及如何将深度学习付诸实践则是未来教育改革发展的重要任务．2005年，上海师范大学黎加厚提出了“深度学习”的概念，并阐述了国外在“促进学生深度学习”方面的研究成果．2007年，华中师范大学郭元祥和他的团队开展了深入的教学改革实验．这次实验以培养学生的主体能力为目标，以价值观、知识观、学习观和过程观的重建为基础，引导实验学校从观念到实践，体验一整套思维和行为模式的转变．2014年，教育部基础教育课程教材发展中心启动深度学习教学改进项目，《“深度学习”教学改进项目实验工作方案》中指出：“深度学习是指在教师的引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程．”这里就是基于这个概念展开研究的．

1 深度学习的内涵

1.1 教育学中的深度学习

对于学生而言，深度学习是一种基于理解的学习．安富海认为：“深度学习是指学习者以高阶思维的发展和实际问题的解决为目标，以整合的知识为内容，积极主动地、批判性地学习新的知识和思想，并将它们融入原有的认知结构中，且能将已有的知识迁移到新的情境中的一种学习．”[7]而对于一线教师，深度学习强调教师应该更注重人的发展．庞舒勤和赵庆林认为：“深度学习强调学生的发展需求，注重调动人的内在潜力，让学生在有效价值判断的基础上学习新知识并有策略地融入自身原有的认知结构，以统整的眼光发现问题、解决问题．”[8]

聚焦于数学教育，首先，数学教育中的深度学习应该围绕数学的核心内容展开．“基于核心问题的数学深度学习，把学习置于复杂的、有意义的、真实的问题情境中，通过引领学生真正经历数学核心问题的探究过程，走向数学意义的深刻理解和深度建构，进而优化学生的数学认知结构，提升学生的数学核心素养．”[9]其次，深度学习的重点在于关注学生的学习过程．在这个过程中，教师为学生创设深度探究的情境、开发具有挑战性的学习主题，引领学生全身心积极参与、体验成功、获得发展，在师生共同努力下实现数学知识的有意义学习．

1.2 计算机科学中的深度学习

“深度学习”的概念源于人工神经网络的研究．1943年，心理学家McCulloch和数学家Pitts参考了生物神经元的结构（如图1），发表了抽象的神经元模型（如图2）．

图1 神经元的结构

图1中有如下几个重要的部分：树突、轴突、轴突末梢以及突触．人脑认识世界的过程如下：第一，神经元通常具有多个树突，主要用来接受传入信息；第二，轴突只有一条，轴突尾端有许多轴突末梢可以给其它多个神经元传递信息；第三，轴突末梢跟其它神经元的树突产生连接，从而传递信号．这个连接的位置在生物学上叫做“突触”．

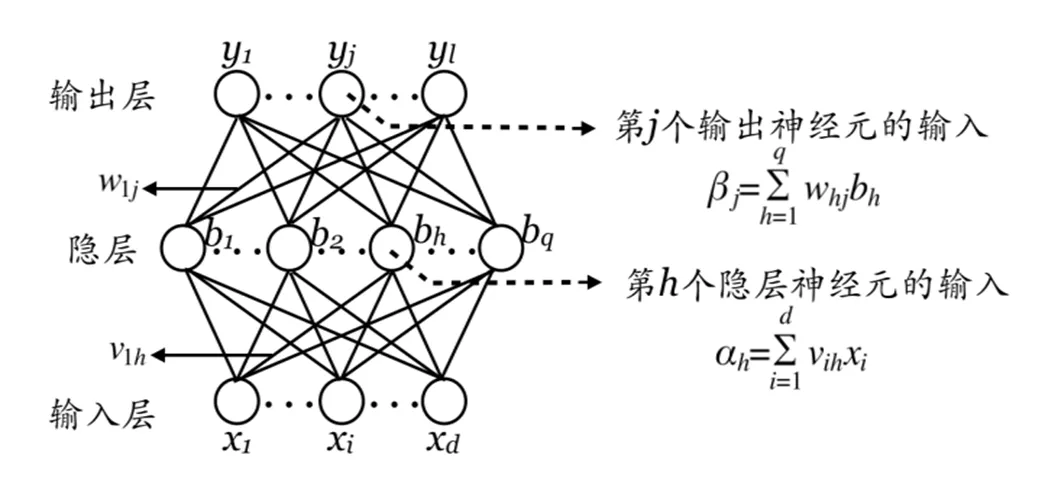
图2 神经元模型

图3 含多个隐层的深度学习模型

1.3 两个领域中“深度学习”的关系

如果说计算机科学里的深度学习是通过激活神经元和计算神经元之间的权重来达到智能的效果，那么教育学里的深度学习，则是在教学实践中通过激活学生已学知识以及明确新旧知识之间的关系来实现教学目标．大家可以清楚地看到计算机科学中深度学习的“模型”对应教育学中基于深度学习的教学过程，且在目标、方法和重点等方面也有着明显的对应关系（见表1）．

表1 两个领域中深度学习的对应关系

从上述两个领域间深度学习的对应关系来看，还可以得到它们的区别．这些主要体现在如下几个方面．

首先，机器没有自主建立模型的能力，而教育学中深度学习的目标之一就是希望学生能够自主地挖掘知识间的联系，这也是“人”和“机器”最本质的区别．

其次，对于机器，面对相同的输入和输出，模型的建立大致是相同的．但是对于教学，每个学生面对新知识往往有着不同的知识建构，被激活的知识也有可能不同．

最后，虽然这两个领域深度学习的实现过程大致相同，但在计算机科学中，深度学习需要利用“题海战术”的方式，使用大量的数据来得到模型；而在教育学中，教师应该更关注学生知识的激活，给学生的练习不宜太多．

2 深度学习的教学过程

深度学习的教学实践围绕学科的核心内容展开，这就要求教师为学生创设适合深度学习的情境，从而促进学生的整体发展．在领会深度学习含义的基础上，深度学习的教学过程应包括：布置学习任务、主动探究并激活知识元（关于知识元的概念，参见2.2）、获取数学本质、巩固知识元之间的联系、总结学习过程．

2.1 布置学习任务

布置学习任务的目的是使学习者带着任务进行自主学习．学习任务的选择既要符合教学目标的要求，也要适当增加一些难度，对学生来说要具有一定的挑战性．这些任务可以是数学知识本身，也可以来源于现实生活，由教师创设丰富而复杂的教学情境．

2.2 主动探究并激活知识元

这个环节是指学生对教师布置的学习任务进行深度探究，主动建构自己的问题解决方式和方法．学科的核心内容是开展深度学习的载体，一类核心内容由几个学习单元组成，一个学习单元又由若干个知识点组成，这些基本构成元素可以称之为知识元．主动探究的过程以学生为主体，希望学生能够将新知识与旧知识建立联系，尽可能多地激活认知结构中已有的知识元．学生激活的知识元越多，就越有可能接近数学本质．

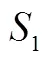
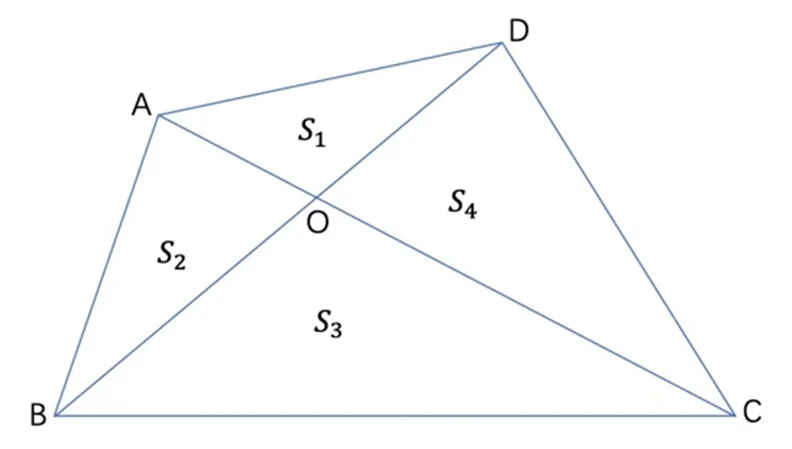
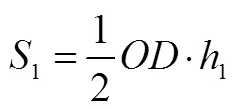
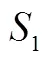
事实上，“蝴蝶定理”的证明难度并不大，但其证明过程有很多需要激活的知识元，例如比和比例、三角形面积的计算、字母表示数、简易方程、等量代换等，这些都是该课学习过程中学生可能激活的知识元．学生只有激活“蝴蝶定理”背后的知识元，才能顺利地获得数学本质．

2.3 获取数学本质

这个环节是指学生在教师的引导下，利用被激活的知识元来获得数学本质．如果学生不能通过自主探究完成深度学习，教师可以适当引导，提示学生该任务与哪些知识元有关，再让学生进行激活，将学生自主探究和教师引导统一起来．这一过程以教师为主导，意在帮助学生获取真正的数学本质．

仍然以“蝴蝶定理”的证明为例．对于小学生而言，该定理的数学本质可以概括为以下两点：其一是用字母表示未知量，使用字母进行运算；其二是利用三角形面积公式，将面积的比值转换成“底”的比值．因此教师在实际教学过程中可以从这两方面加以引导，提示学生有关的知识元，再让学生自己进行激活，并利用激活的知识元来获得数学本质．

2.4 巩固知识元之间的联系

这个环节也可以称为“持续性评价”，即多次进行评价判断学生是否“学会”．科学的持续性评价可以改进教师的教学，促进教师的专业发展；可以优化学生的深度学习，促进学生的全面发展．评价方式有练习课后习题、进行单元测验等．对于任意四边形“蝴蝶定理”的证明，教师可以在学生证明完成之后，再让他们完成如下任务（如图5）．

图5 任意四边形“蝴蝶定理”练习题

题目的问题是和的比值，由于和是已知量，那么求和的比值就可以转化为求和的比值．从图中可以看出，和在两个同底的三角形中，恰好符合“蝴蝶定理”的本质．通过上面的例题，教师可以引导学生进一步理解“蝴蝶定理”的证明过程，让学生应用该定理解决问题，巩固知识元之间的联系，最终达到深度学习的目的．

2.5 总结学习过程

总结学习过程是指让学生回顾自己所参与的有意义的学习过程．教师可以根据学生的总结，判断学生是否已经将新知识与旧知识融为一体，简单说就是“会学”．其深层次目标是为学习新知识做准备，鼓励学生养成总结学习过程的习惯，主动进行深度学习，希望学生达到“会学”的目标．

上述教学实践与计算机科学中深度学习的实现过程有如下对应关系（见表2）．

表2 计算机科学中深度学习与深度学习教学实践的实现过程对比

3 基于深度学习的教学案例

根据以上对深度学习内涵的理解和深度学习教学实践的探讨，下面以义务教育课程标准实验教科书《数学》（六年级上册）“位置与方向（二）”的研究过程为例，对深度学习的教学实践进行深入分析和解读．

该节课的主要教学任务是研究确定位置的要素和方法．教学难点是在学习过程中，发展学生的合情推理能力，使学生能进行有条理地思考，能比较清楚地表达自己的思考过程和结果．

一线教师在进行教学时通常会采用以下流程（如图6）：首先，教师直接给出台风相对于A市的方向和距离，即确定位置所需要的两个因素；其次，让学生根据已知信息确定台风的位置；最后，通过教材中的例题，让学生巩固该节课的重、难点．

这样的设计很难达到深度学习的效果，学生虽然可以很快掌握该节课的数学知识，但是由于教师没有给出具有挑战性的任务，学生没有主动地激活知识元，因此学生只是“学会”知识，而没有达到“会学”知识．

3.1 布置学习任务

学生在该节课之前已经学过多种确定位置的方法，教师在授课时不必给出如此多的信息，可以仅提供台风的位置图作为“具有挑战性的学习主题”，如：目前台风中心正以20千米/时的速度沿直线向A市移动，精确的确定台风中心位置十分重要．如图7所示，假设自己的位置在A市，你有哪些方法可以确定台风中心的位置？由学生自己激活相关的知识元，探索出台风的位置该如何确定，以达到深度学习的目的．

图7 “位置与方向”学习任务

3.2 主动探究并激活知识元

“位置与方向（二）”这一教学内容是基于认识前后、上下、左右，了解东、南、西、北4个方向和认识数对之上的，学生在前期的学习中，已经会用前后、上下、左右描述位置，熟悉8个方向，掌握了数对确定位置的方法，这些都是该课学习的基础．

学生在没有预习的前提下，完成学习任务单的情况如图8所示．

学生主动激活的知识元有：

（1）以A市为中心，学生想到了用数对来描述台风中心的位置．

（2）给出A市到台风中心的距离，学生可以想到“方向”这个重要的要素．这也就是在教师的引导下，学生激活了“方向”这个知识元．事实上，知道A市到台风中心的距离，也就可以确定台风中心在以A市为圆心、距离为半径的圆周上，再知道方向或角度就可以确定台风中心的位置．

突破了“方向”这个知识点后，教师便可以引导学生回忆与方向有关的知识，比如“东南西北”4个方向、“上下左右”4个方位，等等．最终，希望学生回忆到决定“方向”的数学本质就是“射线”．结合之前学过的4个方向，这4个方向本身就在一个坐标系中，在处理问题的过程中学生发现台风中心的位置在东和南之间，很容易引出角度这一要素．

总之，该部分是这节课的关键，在“隐层”中的知识元包括两点之间线段最短、方向、射线、角度、度量以及数对等．虽然在这节课中教师很难让学生激活上述所有的知识元，但让学生经历上面的思考过程，有助于他们利用已有知识来解决问题．只有这样，才能为他们获得数学本质打下基础．

3.3 获取数学本质

学生经历过探究过程并激活知识元后，教师应该进行适当引导：如果只知道“方向”这个条件，能够确定物体的具体位置吗？引导学生得出如下结论：要确定物体的具体位置必须知道两个要素，即物体关于观察点所在的方向和物体在这个方向上与观察点的距离，简单地说就是要用“方向+距离”的方法来确定物体所在的具体位置．

另外，学生要理解角的形成过程，即先确定一条射线作为角的一边，再将射线以顶点为中心旋转，确定另外一条射线，最终形成一个角，充分理解“东偏南”等术语．

3.4 巩固知识元之间的联系

通过课后习题和反复提问来达到目标：学生除了要正确回答问题，还需要利用已有的知识解释自己的答案．具体地说，学生需要了解方向和射线、角度和射线的联系，确定位置的两个要素，掌握确定位置的方法，能根据方向和距离确定物体的位置．

3.5 总结学习过程

通过这节课学生知道要确定物体的位置，关键需要方向和距离两个条件．然后通过回顾学习的整个过程，体会如何通过激活知识元（方向、射线、角度、距离等），发现和探索出描述物体位置的方法，使深度学习真正发生．

该节课的具体流程如图9．

图9 基于深度学习的教学过程

4 总结

深度学习的终极目标是希望学生能够在学习基本数学知识的过程中，自主挖掘相关知识的联系，深刻理解数学本质，最终由“学会”走向“会学”．而作为一线教师，需要在深度学习理论的指导下，设计具有挑战性的学习主题，给学生能够实现深度学习创造良好的条件．根据上面的讨论，教师应注意以下几个方面．

第一，学生进行深度学习的必要性是由数学知识本身决定的．当数学知识有限时，教学过程很像人工神经网络的实现过程，“隐层”中的知识元联系很少．但随着学生学到的数学知识增多，教学过程应基于计算机科学中深度学习的实现过程，“隐层”中知识元的联系也越来越复杂．例如“位置与方向”这节课，射线、角度、度量、数对等都是“隐层”中的知识元，它们的联系在授课中应该让学生领会．

第二，学生能够实现深度学习，绝不是某一节课的任务，而是一个长期的过程．在中、低年级，教师的引导可能起到关键作用，教师可以主动地引导联系学生已学过的知识，但也要尽可能多地给学生自主思考的时间．到了高年级，起关键作用的应该逐步转移到学生，强调知识间联系、一题多解以及充分交流．

最后，教师在教学过程中，应尽量让学生自己建构知识体系，形成自主学习的习惯．在总结一节课的成果时，不要只问学生“学到了什么”，还应该问学生“用到了什么”，让学生回忆学习的过程，只有这样才能让学生逐步“会学”数学．

[1] 郑毓信．小学数学教师专业成长的“中国道路”[J]．数学教育学报，2018，27（6）：1–6．

[2] 毕渔民，王玉文．构建五环综合数学活动教学形式的探索与实践[J]．数学教育学报，2015，24（2）：12–16．

[3] 温建红．论教学课堂预设提问的策略[J]．数学教育学报，2011，20（3）：4–6．

[4] 宋运明．论教学问题提出和数学活动经验的关系[J]．数学教育学报，2010，19（6）：34–36，49．

[5] 仲秀英．促进学生积累教学活动经验的教学策略[J]．数学教育学报，2010，19（5）：36–39．

[6] 顾继玲．聚焦“基本数学活动经验”[J]．数学教育学报，2016，25（1）：34–37．

[7] 安富海．促进深度学习的课堂教学策略研究[J]．课程·教材·教法，2014，34（11）：57–62．

[8] 庞舒勤，赵庆林．让学生体验深度学习——以小学数学教学为例[J]．人民教育，2013（22）：38–40．

[9] 王志南．聚焦核心问题，引领儿童走向数学深度学习[J]．教学与管理，2018（26）：29–31．

[10]  HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets [J]. Neural Computation, 2006, 18 (7): 1 527–1 554．

[11] 马云鹏．深度学习的理解与实践模式——以小学数学学科为例[J]．课程·教材·教法，2017，37（4）：60–67．

[12] 郑毓信．“数学与思维”之深思[J]．数学教育学报，2015，24（1）：1–5．

[13] 周淑红，王玉文．小学数学核心素养的特质与建构[J]．数学教育学报，2017，26（3）：57–61．

The Meaning of Deep Learning and Its Teaching Practice: With A Focus on Elementary Mathematics

YU Ran1, ZHAO Shi-en2

(1. School of Mathematics and Information Technology, Hebei Normal University of Science & Technology, Hebei Qinhuangdao 066004;2. Elementary Education College of Capital Normal University, Beijing 100048, China)

Deep learning in computer science and deep learning in education are very different in its meaning and scope. However, their implementation processes are closely related. This is because deep learning in computer science is essentially an algorithm that simulates the human brain to understand the world. Firstly, we clarify the meaning of deep learning in education, and the relationship between deep learning in the two fields is discussed. Secondly, on the basis of analyzing the implementation process of deep learning in computer science, some key steps of instructional process for the deep learning are explained in detail. Finally, we present a teaching case, namely “location and direction”, and describe the whole process of instructional process for the deep learning.

deep learning; primary school mathematics; teaching practice

G622

A

1004–9894（2021）01–0068–06

于然，赵世恩．深度学习的内涵与教学实践——以小学数学为例[J]．数学教育学报，2021，30（1）：68-73．

2020–10–05

国家自然科学基金项目——随机赋范模理论在两种拓扑下的进一步研究（11401399）

于然（1994—），女，河北唐山人，硕士生，主要从事数学课程与教学论研究．

[责任编校：周学智、张楠]