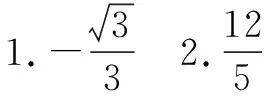一道经典三角高考题的多角度思考

田发胜

(山东省淄博四中 255100)

这是一道起点低，入口宽，既注重考查基础知识，又侧重于考查思维能力的好题.该题从不同的角度入手，有着多种不同的解法，且各种解法难易，繁简程度差别很大，充分体现了各种不同的思维层次，有着较高的选拔功能.

思路1求三角函数值，关键是求出sinα,cosα的值，因此，利用同角三角函数关系式与已知条件结合，有如下解法：

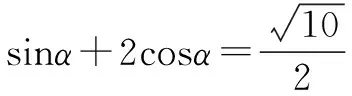
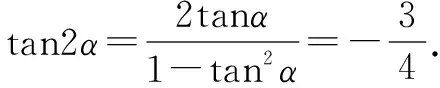
点评这种解法思路清晰，自然，但计算量较大.

思路2求tan2α的值，若能求得tanα的值，再利用二倍角公式，就能轻松获解.由此有下面的解法.

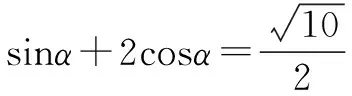
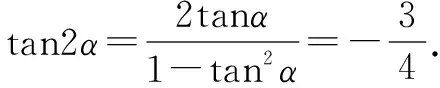
点评这种解法把已知条件进行平方，得到了我们熟悉的“齐次式”结构，直接求得了tanα，使得解题过程得以简化，这是一种整体意识，思维上比解法1进了一步.

思路3已知条件中的角是α，而要求解的问题中的角是2α.因此，求tan2α的值，把已知条件中的角向2α转化.

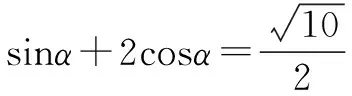
点评这种解法从角的不同入手，首先想到变换角度，把角统一起来，使得计算过程大大简化.在三角变换中，优先考虑角的变化是解三角题的重要思路.

思路4观察sinα+2cosα的结构，联想到辅助角公式，利用辅助角公式获解.

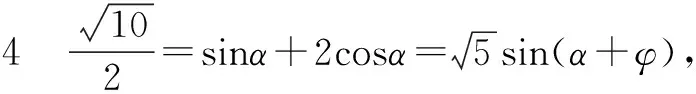
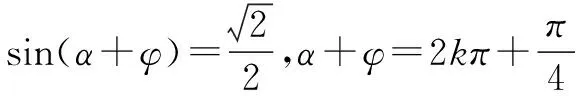
点评辅助角变换是逆用三角变换公式的一种重要形式.利用辅助角变换，把要求解问题中的角用引入的辅助角表示出来，使得问题得以获解.

思路5这是一个选择题，解选择题应“不择手段”，仔细观察题目的结构特征及数字信息，直接获得sinα,cosα的值，使得问题获解.

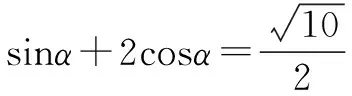
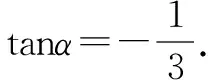
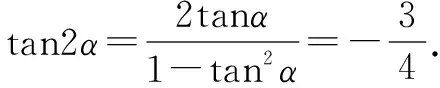
点评解选择题以快为上，不需要过程，因此，特殊值法是一种重要的解题方法.但需要同学们有敏锐的观察能力，在三角函数中，利用勾股数类比sin2α+cos2α=1是重要的法宝.

三角函数公式众多，灵活多变，许多同学在学习过程中陷入其中，绕不出来.实际上，解三角题时，同学们只要抓住弦切的互化，公式的灵活运用，角是否有变化等基本规律，然后仔细观察题目中的结构特征，数字信息，找出已知条件和求解的问题之间的差异与联系，抓住角度是否发生了变化这个关键，再选择合适的公式，消除角度的差异，函数名称的差异，就能获得解题思路，使得问题得以解决.

咱们再来看一个例子.

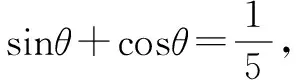
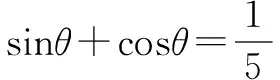
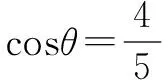
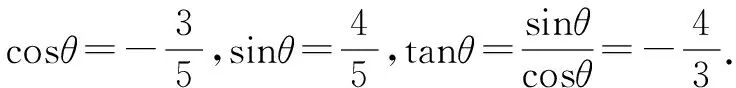
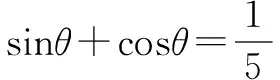
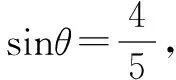
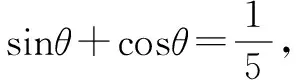
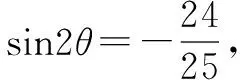
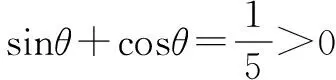
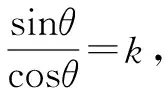
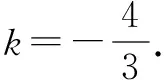
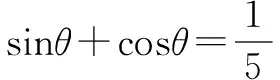
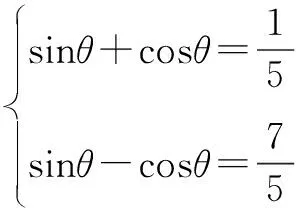
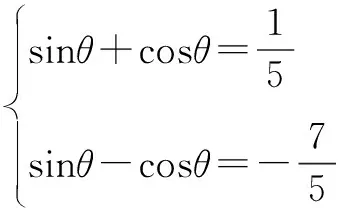
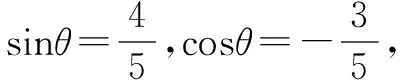
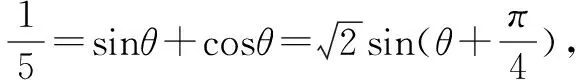
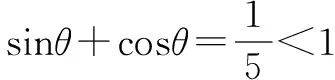
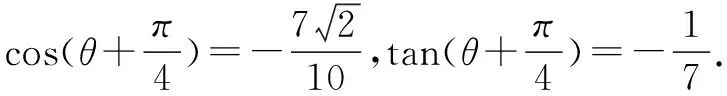
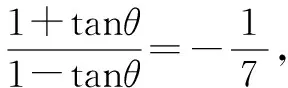
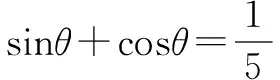
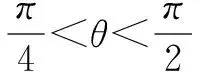
本例与上面的例子相比较，给出了角的范围，因此，在解题过程中不要忽视角的范围，应注意根据给出的数字的大小，适当地缩小角的范围，或者对求得的结果进行检验.

下面再提供几题，作为练习，请同学们仔细观察题目中条件的结构特征，给出的数字信息，从多个角度入手，给出不同的解法，并认真比较，寻求最优解答，以期能启迪同学们的思维，开阔同学的眼界，获得灵活处理问题的思维方法.