优化学习路径 培养科学思维——浅谈复合场中“有效最低点”的几种求法

严 霓

(江苏省常州市金坛区第一中学 213200)

物理核心素养是学生在接受物理教育过程中逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力，是学生通过物理学习而内化的带有物理学科特性的品质，是学生科学素养的关键成分，科学思维是从物理学视角对客观事物的本质属性、内在规律及相互关系的认识方式；是基于经验事实建构物理模型的抽象概括过程；是分析综合、推理论证等方法在科学领域的具体运用；是基于事实证据和科学推理对不同观点和结论提出质疑和批判，进行检验和修正，进而提出创造性见解的能力与品格.主要包括四个内容：模型建构、科学推理、科学论证、质疑创新.

教师在平时教学中，注重优化学习路径，让学生经历具体的学习过程，培养科学思维，复合场中的“有效最低点”问题是高考的重点，也是难点，而曲线运动中一种特殊的运动——圆周运动，也是常考的一种形式，复合场竖直平面内的圆周运动，是圆周运动的常见模式，而竖直平面内的圆周运动的有效“最低点”是解决这一类问题的关键点，对于“有效最低点”的位置的求法，很多同学把握不住，不知道怎么求，基于这个情况，本人总结了几个有效最低点的几种解法.

例题如图1所示,水平方向的匀强电场中，有一质量为m的带电小球，用长为L的细线悬于O点，当小球平衡时，细线和水平方向的夹角为θ，现给小球一个初速度.速度方向和细线垂直，使小球恰能在竖直平面内做圆周运动，则圆周运动过程中速度的最小值为多少？

解析此时最高点的速度并不是最小速度，最低点也不是最大速度的位置，它的“等效最低点位置”在哪?又如何求等效最高点的位置?

关于“等效最低点”的位置，本人总结了下，我们可以从以下几个方面来找“等效最低点”.

解法一等效替代法， 复杂问题简单化

方法依据既有重力场和匀强电场，但合场也是恒定不变的，与处理重力场类似.所以可以把重力和电场力合成，求出合力，把这个合力等效成“重力”，我们把该合力称之为“等效重力”，此时相当于只有“重力”作用 ，那么运动过程中沿着等效重力的方向，该点则为等效最低点.(如图2的M即为“等效最高点”，N点即为“等效最低点”)

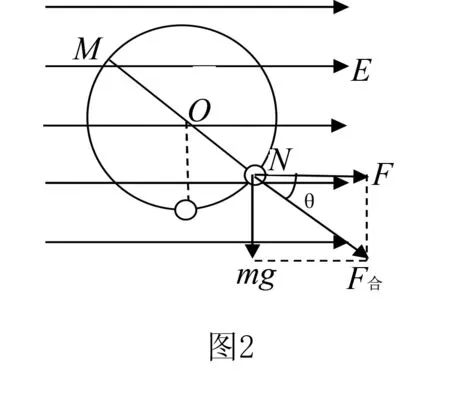
解题策略电场中带电粒子在竖直平面内做圆周运动：

等效“最高点” ：物体速度最小，绳的拉力最小.

特点：mg和Eq的合力与绳的拉力在同一直线上，且方向相同.

等效“最低点”：物体速度最大，绳的拉力最大

特点:mg和Eq的合力与绳的拉力在同一直线上，且方向相反.

所以,速度最小值为“等效最高点”(M点)

解法二动力学法，运动情景清晰化

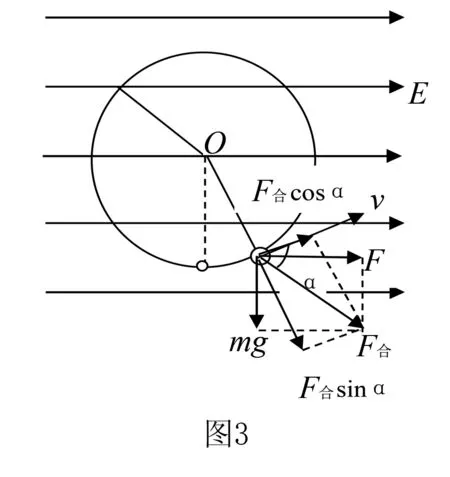
方法依据如图3，我们找某一位置进行受力分析，把重力和电场力合成一个力F合，而合力F合产生两个效果，一个是沿速度方向(切线方向)，一个沿半径方向，沿速度方向，用来改变速度的大小，我们可以发现，当F合有速度方向(切线方向)分量时，速度的大小就改变，而我们的“最低点”的速度最大，所以只有当F合与绳的拉力(半径方向)在同一直线上，F合就没有速度方向的分量，这时速度就最大或最小.

解题策略我们从受力分析可以得出，合力F合所在的延长线必须为直径时，就没有速度方向(切线方向)分量，该延长线与圆的交点为“最高点”、“最低点”.

所以我们求速度最大值，可以得出

解法三功能关系法，解题目标明确化

方法依据1.功能关系依据：最低点特点：速度最大，动能就最大.

解题策略当物体运动到合外力与位移夹角小于90度时，合外力做正功，动能逐渐增加(如图4甲)； 当物体运动到合外力与位移夹角大于90度时，合外力做负功，动能逐渐减小(如图4乙)，所以当物体运动到合外力与位移夹角等于90度时(即垂直时)，此时动能最大，此时合外力的反向延长线正好经过圆心.如图4丙所示.

解法四数学最值法，物理问题数学化

方法依据1.依据三角函数求最值

2.数学最值法具体解法

根据“等效最低点”速度最大，可知，动能最大.

即求

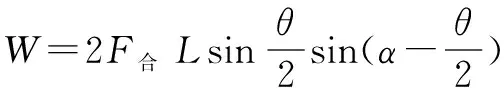
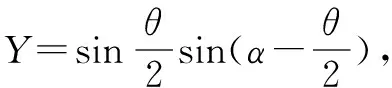
即求Y的最大值

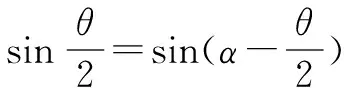
所以“等效最低点”和圆心的连线与F合方向平行，速度最大.

得出“等效最低点”的反向延长线经过圆心.

本文对“有效最低点”的找法，做了一点粗略的介绍，希望对读者有一定的帮助，有不足之处，还望大家批评指正.