基于等效电导率的压接型IGBT器件温度场仿真

何智鹏，李岩，侯婷，姬煜轲

(直流输电技术国家重点实验室(南方电网科学研究院)，广州510663)

0 引言

压接型绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)器件具有无焊接点，无引线，低热阻的特点，因此其流通能力相较于传统的焊接式IGBT器件由较大提高，因此常被应用在高压大功率场合[1]。随着近年来大容量柔性直流输电工程的大规模建设，对于压接型IGBT器件的使用将越来越多，大有取代传统焊接式IGBT器件成为市场应用主流的趋势[2]。因此，对于运行状态下压接型IGBT器件可靠性研究以及寿命预测有十分重要的意义[3 - 4]。

由于没有焊层和键合引线，压接型IGBT器件的失效模式与传统焊接式IGBT器件存在差异，主要存在微动磨损，弹簧失效，芯片断裂等几种失效模式[5 - 6]。究其原因，都是由于在器件工作时，芯片产生周期性的温度波动，由于多层结构不同材料之间热膨胀系数(coefficient of thermal expansion, CTE)存在差异，使得接触面上产生热应力，导致材料出现老化，进而导致器件失效[7]。因此，得到运行状态下压接型IGBT器件内部温度分布，对于器件可靠性评估以及寿命预测存在重要意义[8]。

有限元分析(finite element analysis, FEA)是压接型IGBT器件温度分布计算的常用工具，而有限元模型的准确性极大地影响仿真计算结果[9]。对于压接型IGBT器件温度场仿真，设置基于工况的芯片载荷对于模拟实际工况下该器件内部温度分布十分重要，然而现有研究对该问题涉及不多。文献[10]通过对整体器件的导通损耗以及开关损耗的计算得到器件内部总的发热功率，再对每个芯片取平均值作为单个芯片的发热功率。这一方法没有考虑由于几何不对称性以及温度不均匀造成的器件内部芯片之间发热功率的差异。文献[11]考虑了器件内芯片发热功率接触电阻接触热阻以及温度分布影响呈现的差异性，但未控制器件集电极电流为定值，因而会导致单个芯片发热功率总和超过器件整体发热功率问题。文献[12]建立了单芯片有限元模型，控制母线电流为50 A恒定，然而文献中简化模型与实际压接型IGBT器件还存在一定差异。本文提出了基于工况的压接型IGBT器件内部温度分布预测仿真办法，通过提出芯片等效电导率概念，以反应芯片损耗随芯片结温变化的特性，以及由于几何不对称和温度分布不均匀造成的芯片间损耗差异的特性，该仿真办法能够更加准确地反映系统运行时，压接型IGBT器件内部温度的分布情况。另外，本文还应用该仿真方法，对三相MMC系统进行仿真分析。

1 压接型IGBT结构

图1为某型号压接型IGBT器件3D模型。

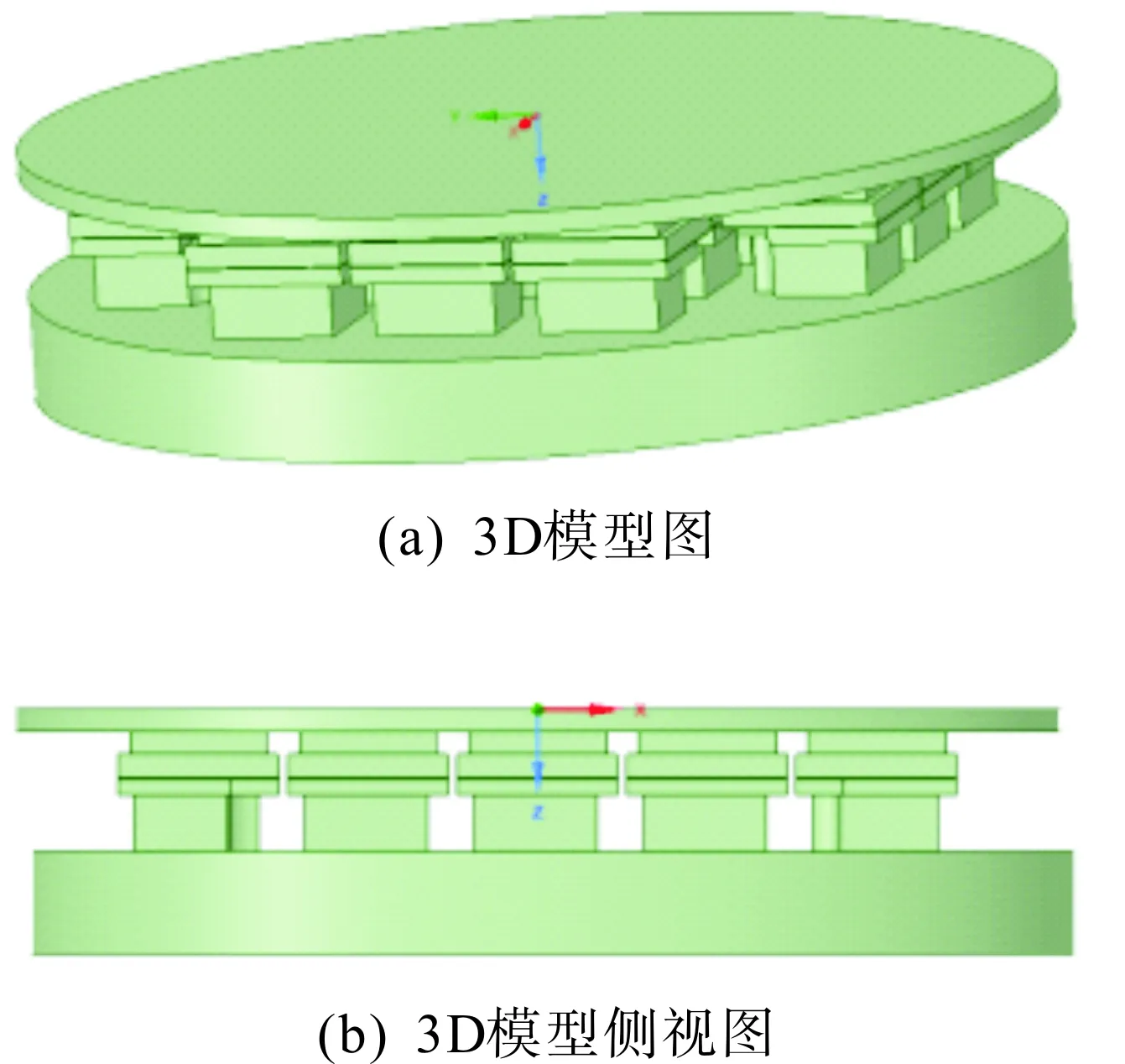
图1 某型号压接型IGBT器件结构示意图Fig.1 Sketch diagram of the structure of a press-pack IGBT module

图中自下而上依次为集电极凸台、集电极钼片、芯片、发射极钼片和发射极凸台。整个器件包含21块芯片，此外，门极弹簧、印刷电路板(printed circuit board, PCB)等结构在建模中忽略。整个结构由外部装配力紧密压接，底部放置碟簧以平衡热应力带来的形变。

2 基于等效电导率的压接型IGBT器件仿真模型

有限元仿真是得到压接型IGBT器件内部温度分布的重要方法，而芯片发热功率的设置对于仿真结果的准确性有很大影响[13]。本文提出了基于等效电导率的思想进行仿真载荷设置。

当电流流过器件时，由于几何的不对称性，器件内部各芯片上流过电流不相等，电流的不均衡导致发热功率差异，进一步引起结温分布不均匀，而结温又对芯片发热功率产生影响[14]。因此，本文引入了芯片等效电导率，即设置芯片材料电导率与温度相关以反映芯片发热功率随温度变化的特性，使得当额定电流流过功率器件时，芯片总产热量与器件产热量相等。这时，芯片上发热功率分布就是压接型IGBT器件运行工况下的分布情况。

具体的原理为，假设IGBT器件运行时，内部损耗过程为欧姆损耗，即：

p=f(Tj)=Ic2R(T)

(1)

式中：Tj为芯片结温；IC为器件集电极平均电流；R(T)为由温度决定的芯片等效电阻。而芯片材料的电导率，可以通过电阻公式推导如式(2)所示。

(2)

式中：L为芯片厚度；S为器件内部所有芯片总面积。综合以上两式，可以得到一个和温度直接相关的芯片电导率的计算公式如式(3)所示。

(3)

式中P(T)为随温度变化的芯片发热功率。

因此，P(T)是计算芯片等效电导率的关键，该发热功率由器件热特性以及运行工况共同决定。随后，以MMC工况为例，进行基于该仿真模型的压接型IGBT器件温度场仿真。

3 MMC结构及工作原理

3.1 子器件工作原理

子器件拓扑结构如图2所示，T1和T2为IGBT，D1和D2为反并联二极管；C0为子器件直流侧电容；uC为电容电压；usm为子器件两端电压也是子器件的输出电压；ism为流入子器件的电流。

子器件上下IGBT T1、T2开关状态以及电流方向ism的不同，会出现子器件“投入”以及“旁路”两种状态，分别对应子器件输出电压为电容电压uC和0 V[15]。

图2 MMC子器件结构示意图Fig.2 Sketch diagram of the structure of MMC sub-module

3.2 三相MMC系统工作原理

三相MMC系统结构示意图如图3所示，每相单元由10个子器件构成，上下桥臂分别有5个子器件。

图3 三相MMC系统结构示意图Fig.3 Sketch diagram for the structure of three-phase MMC system

MMC系统运行满足2个条件：

1)维持直流侧电压恒定。根据图3可知，在假设每个子器件电容电压不变的前提下，就要保证3个相单元中处于投入状态的子器件数目不变且相等。即：

upa+una=Udc

(4)

式中：upa为a相上桥臂投入子器件的总电压；una为a相下桥臂投入子器件的总电压；Udc为系统直流侧电压。

2)在交流侧输出三相交流电压。通过对3个相单元上下桥臂中投入的子器件数进行调节，从而实现三相交流电压的输出，即通过改变每一时刻上下桥臂投入的子器件个数，使得交流侧电压形成正弦波。

4 器件损耗计算

4.1 三相MMC系统电流计算

在MMC工况下，子器件中压接型IGBT器件损耗由运行过程中子器件平均电流和平均电压决定。考虑简化三相MMC系统模型如图3所示，每相上下桥臂各包含5个子器件，其中直流侧电压Udc为±2 250 V，调制比m为0.9，设置单子器件额定电容电压值为900 V。三相负载为阻感负载，电感值L为0.005 H，电阻值R为2 Ω。a相相电压Ua、三相上下桥臂电抗L、a相相电流ia和直流侧电流Idc分别由式(5)—(8)得到。

(5)

(6)

(7)

(8)

桥臂电流iau可由式(9)得到。

(9)

而流经子器件的电流为桥臂电流有效值[16]。

4.2 MMC工况下压接型IGBT器件损耗计算

IGBT器件功率损耗模型中主要包含3个部分的损耗：1)静态损耗，包含通态损耗PTcon和截止损耗；2)开关损耗PTsw，包含开通损耗和关断损耗；3)驱动损耗。其中，IGBT器件的驱动损耗和截止损耗在整体损耗中占很少比重的部分，在本文的计算的精度范围之内可以忽略[17]。

则IGBT总功率损耗PTtot可以表示为：

PTtot=PTcon+PTsw

(10)

式中PTcon和PTsw分别为器件通态损耗和开关损耗。

IGBT通态损耗的计算可以通过拟合集射极电压Vce和电流IC的关系得到，如式(11)所示。

VCE(Tj)=RT(Tj)·IC+VCEO

(11)

式中：Vce为器件导通压降；RT为器件等效通态电阻VCE0为擎柱电压。RT和VCE0都是结温Tj的函数。该函数关系可由器件的数据手册得到。则器件通态损耗PTcon可表示为：

PTcon=VCEIC=(RTIC+VCEO)·IC=f(IC,Tj)

(12)

器件的开关损耗主要由集电极平均电流IC和平均反向电压VDC决定，可近似如式(3)所示。

(13)

式中：Eon为开通损耗，Eoff为关断损耗。EswN为额定反向电压VDCN下开关损耗，为集电极平均电流IC的函数，该函数关系可由器件数据手册给出。

5 仿真计算原理与结果分析

5.1 直接耦合有限元仿真算法

由于芯片等效电导率的设置，整个仿真模型成为了对于温度的非线性系统。具体来说，该仿真模型满足如热传导方程式(14)所示。

(14)

式中：λ为材料热传导系数；H为发热功率；ρ为芯片材料密度；c为比热；T为温度。其中发热功率随温度的变化而变化，因此整个系统呈现出非线性的特点。由于该非线性偏微分方程显式解无法直接求得，因此，这里通过迭代法近似求解。原理如下。

首先，设置温度初值计算得到初始芯片发热功率H0，同时计算得到温度T0，再带入T0计算得到新的发热功率H1，再利用H1计算得到新的温度T1，反复迭代i次后，当Ti与Ti-1的差值小于预设残差后，即认为计算收敛，则Ti就是非线性偏微分方程的近似解，即实际温度分布。

5.2 仿真结果分析

将4.1节工况参数代入式(4)—(9)可求得器件集电极平均电流IC=623 A。另外，根据4.2节的简化计算，我们可以看到，当集电极平均电流IC以及反向电压VDC恒定的情况下，MMC子器件中压接型IGBT器件的总损耗为结温Tj的单值函数，并且可由器件数据手册得到。本文研究对象为某型号压接型IGBT器件，其输出特性曲线以及开关能量曲线如图4所示。读取IC=623 A时不同温度下器件饱和压降以及开关能量，并进行线性拟合，即可分别得到不同温度下压接型IGBT器件导通损耗和开关损耗。通过温度线性拟合，即可得到压接型IGBT器件损耗与结温的关系为：

P(T)=1.359T+581.2

(15)

将式(15)代入式(3)并进行相应化简，可以得到IGBT芯片等效电导率随温度变化的函数为：

σ(T)=11 000/(1.359T+581.2)

(16)

设置模型材料电热属性如表1所示。

图4 器件数据手册曲线Fig.4 Curves of device data sheets

表1 仿真模型材料电热属性Tab.1 Electricthermal properties of simulation model materials

设置电流边界条件为623 A电流从集电极外表面流入，发射极外表面流出。热边界条件为集电极和发射极外表面对流换热系数为1 500 W/(m2·K)，仿真类型为稳态。

仿真经过6次迭代计算，温度残差达到0.05%，表明迭代结果收敛，得到温度分布云图如图5所示。

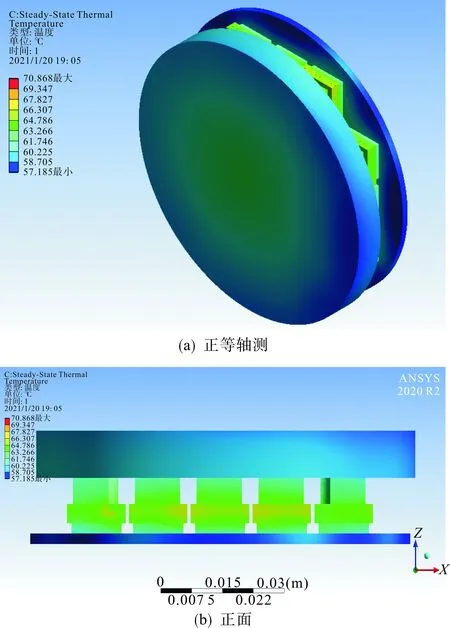
图5 MMC工况下压接型IGBT器件温度分布 Fig.5 Distribution diagram of press-pack IGBT under MMC condition

由图5可知，压接型IGBT器件运行时，存在一定温度梯度。由热传导路径所决定，IGBT芯片温度较高，两侧凸台温度较低。同时，由于各芯片发热功率和散热情况存在差异，导致器件中心温度高于四周。

当IGBT器件工作时，芯片处温度较高，由于芯片表面存在金属镀膜，其在反复的功率循环下会出现裂痕，进而导致器件失效。因此研究IGBT芯片在器件工作时的温度分布有着重要的意义。

如图6所示为工况下芯片表面温度分布。由于电流和温度分布的不均匀，导致器件内部芯片发热功率存在差异，最终导致器件内部温度分布不均匀，其中温度最高处可以达到70.86 ℃，位于中心芯片边缘。温度分布呈现自中心向周围递减的特性。由于器件内部多层结构材料热膨胀系数的不匹配，使得材料连接处产生相对位移的趋势，导致热应力的产生，这种趋势随着连接处温度的升高而增大。所以中心芯片在工况下将承受最大的热应力，最容易出现失效。因此，在子器件阀串散热器设计中，需要考虑增强器件中心散热能力，进而实现降低中心芯片温度，提高子器件运行可靠性的作用。

图6 MMC工况下压接型IGBT芯片温度分布Fig.6 Temperature distribution diagram of press-pack IGBT under MMC condition

6 结语

本文研究了基于等效电导率的压接型IGBT器件芯片损耗建模的方法，通过建立芯片等效电导率与温度之间的关系，反映了IGBT芯片发热功率随温度变化的特性，进一步体现了压接型IGBT器件内部由于温度分布而造成的芯片发热不均匀，提高了压接型IGBT器件内部温度场仿真的准确性。同时，本文在MMC工况下使用该仿真方法进行了温度场仿真，得到了确定的MMC工况下的压接型IGBT器件的内部温度分布规律。该仿真方法对于不同工况具有普适性，因此对于大功率换流器电力电子器件的可靠性分析和寿命预测具有重要意义。