基于VGLESO和滑模理论的直流配电网母线电压控制策略
韩永强,徐明忻,孙碣,孙永辉,赵立军,吴博宁
(1. 国网内蒙古东部电力有限公司经济技术研究院,呼和浩特010020;2. 天津理工大学电气电子工程学院,天津 300384)
0 引言
国内外研究表明,相比于交流配电网,直流配电网在输送容量、系统可控性、经济性以及供电质量方面都具有更加优越的性能[1 - 6]。
当直流配电网与交流电网相连时,往往通过优化三相AC-DC双向变流器的控制电路来实现母线电压的控制[7]。文献[8 - 9]采用传统比例积分双环控制策略来抑制母线电压的波动。PI控制器虽然在工业上得到了大范围的应用,并取得了良好的控制效果。但基于偏差控制原理的PI控制器,很难克服电容元件导致的控制时滞,从而无法满足电力系统的动态性能要求。文献[10 - 11]将模糊PI控制器应用到了电压外环,提高了系统的控制精度和自适应性。但仍未克服因电容两端电压不能突变导致的控制时滞。文献[12 - 13]在双闭环控制的基础上引入了电流前馈控制,明显提高了系统的动态响应,缩短了过渡过程时间。但电流前馈控制的实现需要增设额外的电流传感器,增加了配电网的建设与维护成本。当系统存在多个变流器时,电流传感器的位置选取也变得十分困难。
滑模变结构控制(sliding mode control, SMC)由于对系统数学模型要求不高,且对参数摄动、外部扰动具有较强的鲁棒性,常被应用于难以建立精确数学模型的非线性系统当中[14]。但在传统的滑模控制方法中, 需要较高的控制增益来提高系统的动态性能,过大的增益和控制的不连续性使得系统存在一定程度的抖振,严重影响了滑模控制在实际工程中的应用。
LESO不仅能对系统中的各状态变量进行准确的估计,还能对系统的总扰动进行实时跟踪。为保证LESO具有较高的估计精度,往往采用较高的增益系数,这导致了LESO在初始时刻的观测值普遍存在峰化问题,影响了系统的启动特性。针对高增益LESO存在的峰化问题,本文设计了一种VGLESO,其增益是一个时变函数,在初始时刻增益系数为一个很小的值,随着时间的推移,增益系数逐步变为恒定常数。
在此基础上,本文将滑模理论与VGLESO结合,提出了变增益滑模自抗扰控制策略。该控制策略不仅保留了滑模控制的强鲁棒性,同时还减弱了系统的抖振,提高了系统的动态性能。最后,通过数字仿真验证了该控制策略的可行性与真确性。
1 直流配电网AC-DC变换器数学建模
直流配电网AC-DC变换器的电路拓扑图如图1所示。图中:ea,eb,ec为等效的三相交流电源;ia,ib,ic为交流侧线路电流;R为线路等效电阻;L为线路等效电感;C为直流侧稳压电容;Udc为直流侧电容器两端电压;idc为直流侧两端电流;ic为流过电容器两端的电流;iL是流经负载两端的电流;Load是直流配电网的等效负荷。
根据图1所示的直流配电网AC-DC双向变流器的电路拓扑结构,可得其数学模型:
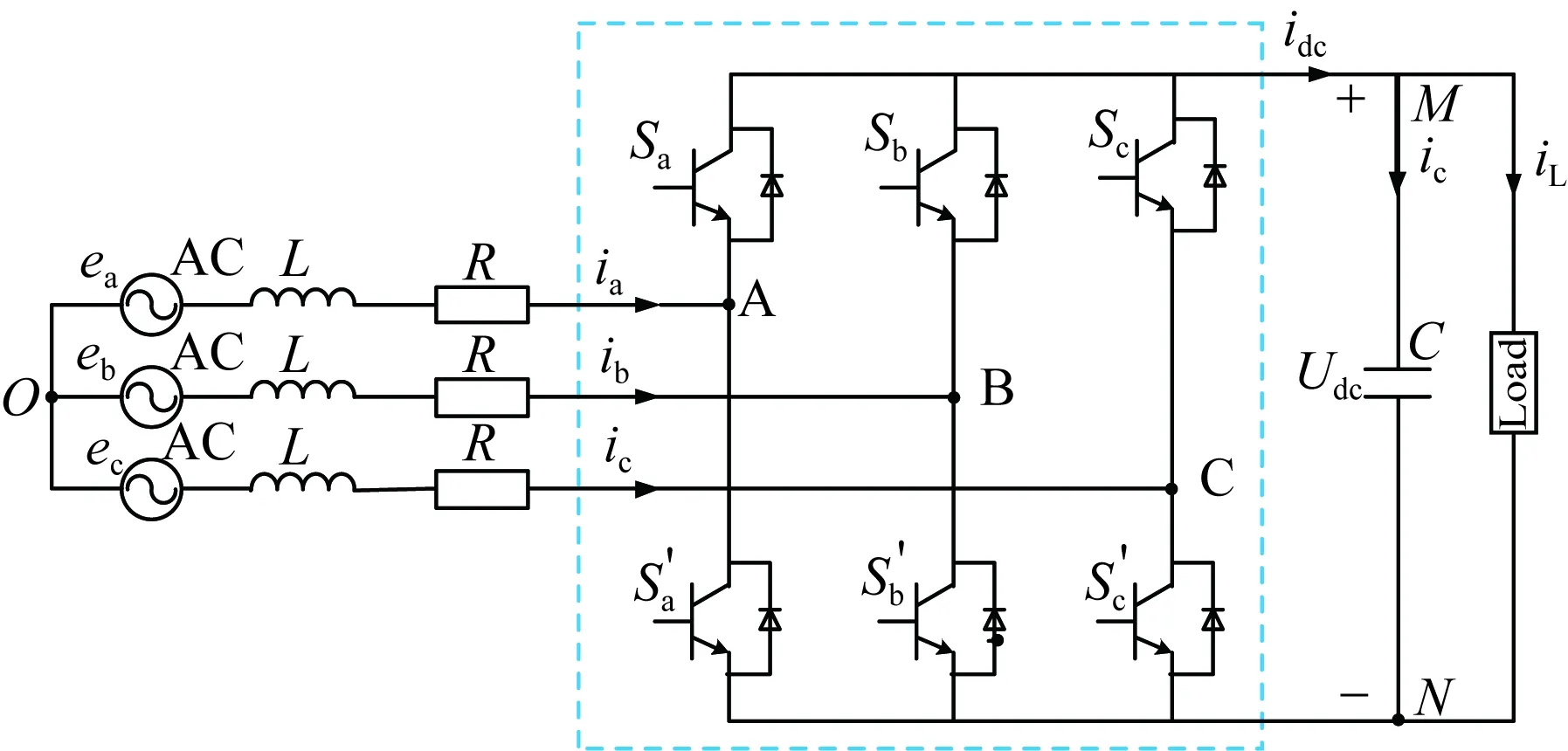
图1 AC-DC变换器电路拓扑Fig.1 AC-DC converter circuit topology
(1)
式中Si为开关函数,具体为:
(2)
三相静止坐标系到两相静止坐标系变换的矩阵为:
(3)
两相静止坐标系到两相旋转坐标系变换的矩阵为:
(4)
式中θ为d轴超前a轴的角度。
坐标变换之后的直流配电网AC-DC双向变流器的数学模型为:
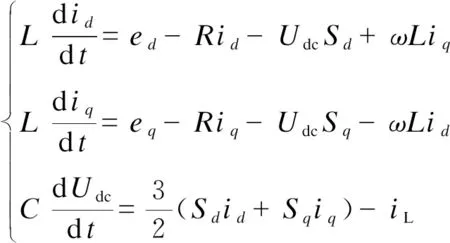
(5)
式中:ed、eq为三相交流电源ea、eb、ec在d轴和q轴的电压分量;id和iq为三相电流ia、ib、ic在d轴和q轴的电流分量;Sd和Sq为开关函数Sa、Sb、Sc在两相旋转坐标系下的函数。
(6)
式(6)两边同时对时间t求导后,再联立等式(5)可得:
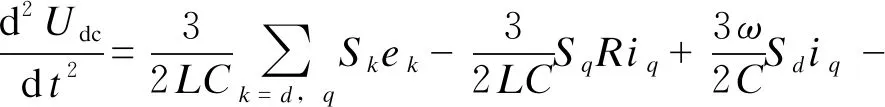
(7)
从式(7)可知,直流配电网AC-DC双向变流器可以看作是一个二阶系统。对于一个可测的二阶系统,可以通过设计合适的线性扩张状态观测器来对系统的状态变量和总扰动进行观测。
2 LESO的观测精度与初始峰化现象的矛盾分析
对于一个二阶非线性系统,有:
(8)



(9)
式中y为系统的输出。
对应的三阶LESO为:
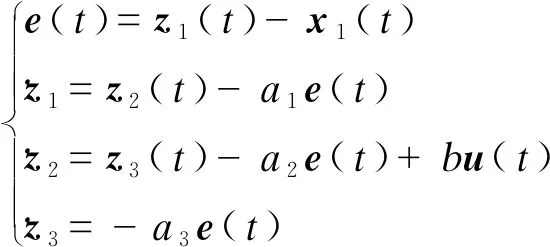
(10)
由式(10)可知:
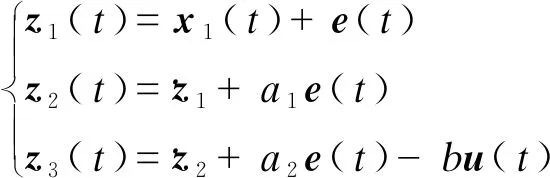
(11)
进而整理得:

(12)
式中:z1(t)、z2(t)、z3(t)为扩张状态观测器的状态变量;a1、a2、a3均大于0,为扩张状态观测器的误差反馈增益。

3 变增益LESO的设计与收敛性证明
3.1 变增益LESO的设计
为了有效抑制高增益LESO在初始时刻输出存在峰值的问题,本文设计了一种变增益LESO,其具体表达式如式(13)所示。
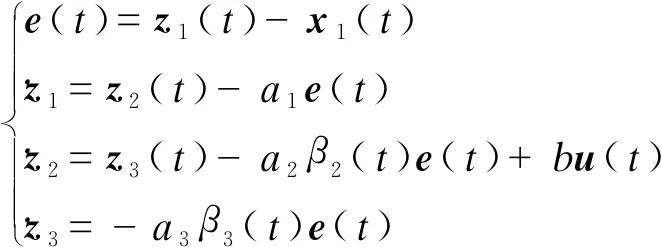
(13)
其中:
(14)
式中:bi用来限定时间t的取值;ni用来限制函数的凹凸性及凹凸程度;1是为了保证参数a1、a2、a3与高增益LESO的参数一致。使得变增益LESO既能有效的抑制初始峰值现象,又能保持传统高增益LESO的高精度跟踪性能。
传统LESO的误差反馈增益选取方法通常是采用极点配置[17]。
式(10)的特征方程为:
p3+a1p2+a2p+a3=0
(15)
将特征方程的极点配置在观测器的带宽ω0处,即:
p3+a1p2+a2p+a3=(p+w0)3
(16)
式中p为拉氏变换算子。
根据恒等式的性质,将式(16)展开得:
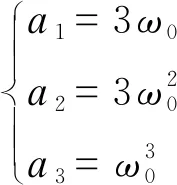
(17)
由此,就把原先对LESO的参数配置问题转化为了对LESO带宽的选取,降低了调参难度。
3.2 变增益LESO的收敛性证明
为了方便证明,取h1=α1,h2(t)=α2β2(t),h3(t)=α3β3(t),将式(13)变为:

(18)
令

(19)
联立式(8)(18)和(19)可得:

(20)
令
(21)
从而可以得到变增益LESO的误差状态方程为:
(22)
式(22)的特征方程为:
(23)
根据霍尔维茨稳定性判据,式(23)只需满足以下条件就能保证式(22)在平衡点(e1(t)=0,e2(t)=0,e3(t)=0)是大范围渐近稳定的,也就是说变增益LESO能够很好地跟踪系统的状态变量和扰动。

(24)
4 滑模自抗扰控制器的设计
为了获得良好的控制效果,选择直流配电网母线电压误差和电压误差的微分信号作为滑模函数的状态变量。
选取滑模函数为:

(25)
根据霍尔维茨稳定性判据,只需要c>0, 式(25)就是大范围渐近稳定的。
上式中:
(26)
式中:Udcr为母线电压额定值;Udc为母线电压实时值。

(27)
根据式(7)知,可以将直流配电网AC-DC双向变流器等效成为一个二阶系统。对于一个可观的二阶系统,可以通过式(13)来对其状态变量和总扰动进行跟踪观测。具体的跟踪方式如式(28)所示。
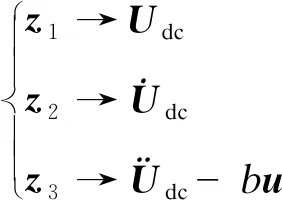
(28)
为了有效地抑制抖振,确保系统状态变量能够在有限的时间内到达滑模面,本文采用指数趋近率来设计滑模控制器。具体形式由式(29)所示。
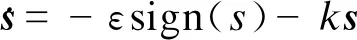
(29)
式中:ε>0,k>0。ε为系统状态变量趋向滑模面的速度,如果ε值太小,那么系统由初始状态到达滑模面所用时间就很长,如果ε值过大,又将会导致系统的抖振,不利于系统的稳定。k为指数趋近项系数,k值变大,将会缩短系统由初始状态到到达滑模面所用时间,但k值的增大,将会减小“滑动模态”的存在区域。一般来说,为了达到良好的控制效果,在调参的过程中,如果增大了ε, 则需要相应的减小k值。
联立式(25—29)可得系统控制率为:
u=b-1(εsign(s)+ks-cz2-z3)
(30)
从式(30)可知,变增益滑模自抗扰控制律u由主要是由非线性的误差反馈率u1(u1=b-1(εsign(s)+ks-cz2))和扰动补偿项u2(u2=z3/b)组成。当系统启动时,母线电压额定值与实时观测值的差值较大,这时系统控制率主要是由非线性的误差反馈率起作用,来确保系统具有良好的启动特性。当系统受到扰动时,扰动补偿器能够根据变增益LESO的观测值迅速做出响应,扰动补偿器的输出值将直接作为电流内环的参考值,克服了电容元件导致的控制时滞,提高了系统的动态性能。
图2为变增益滑模自抗扰控制器的结构示意图,图3为直流配电网AC-DC双向变流器的控制结构图。

图2 滑模自抗扰控制器结构示意图Fig.2 Structure diagram of sliding mode ADRC
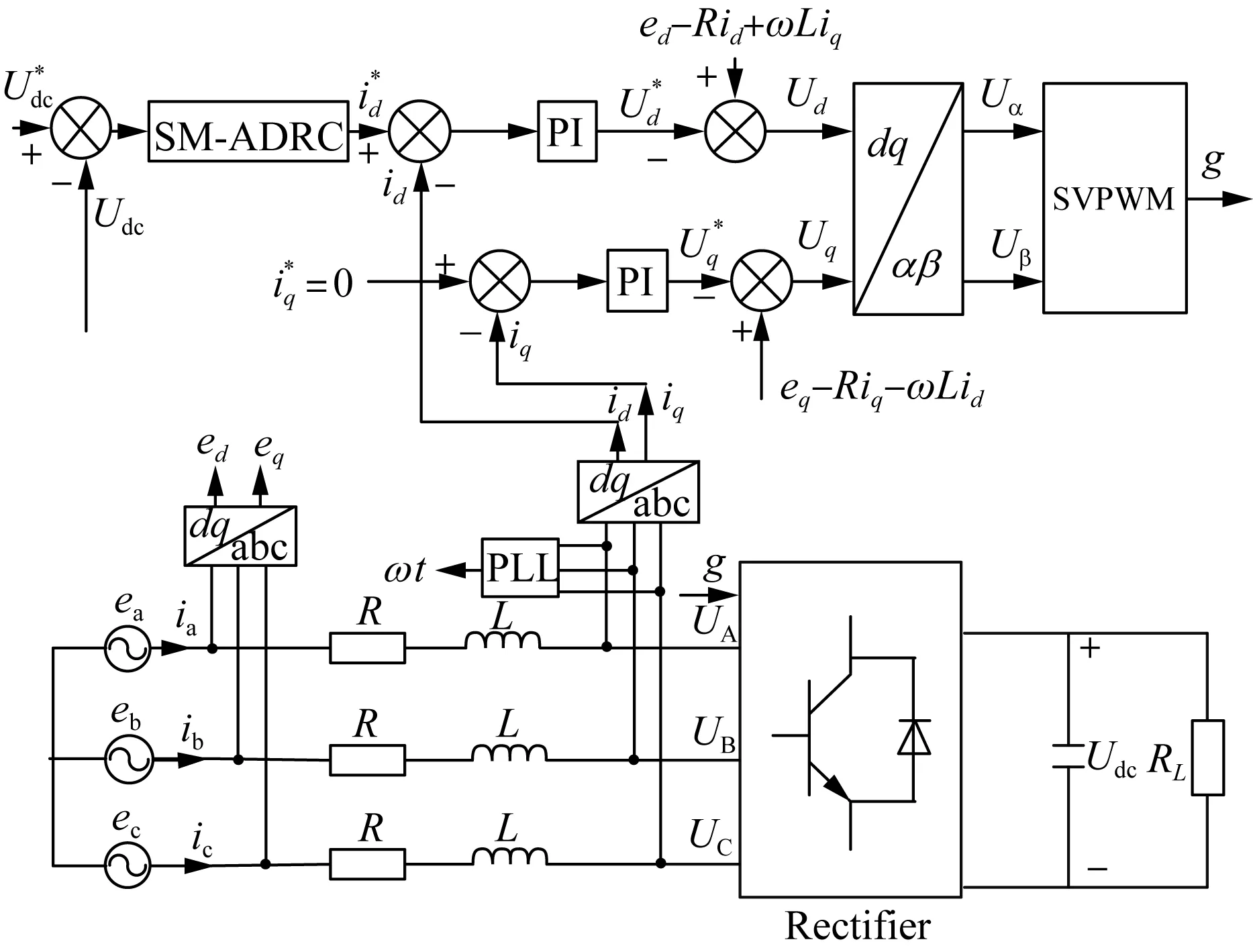
图3 AC-DC变换器控制结构图Fig.3 Control structure diagram of AC-DC converter
以下为滑模控制器的稳定性证明。
基于式(29)所示系统,构建式(31)所示Lyapunov函数。
V(s)=0.5s2
(31)
容易看出V(s)正定,且V(0)=0。进而可得:
(32)
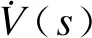
综上,根据Lyapunov第二方法[16]可知,式(29)在平衡状态s=0处大范围渐近稳定,即无论初始电压为何值,状态变量都能在有限的时间内到达滑模面。
5 仿真与分析
为了验证VGLESO对初始峰值的抑制效果以及变增益滑模自抗扰控制器的控制效果,用MATLAB/Simulink 搭建了如图4所示的直流配电网。系统参数和控制器参数如表1和表2所示。

图4 直流配电网Fig.4 DC distribution network
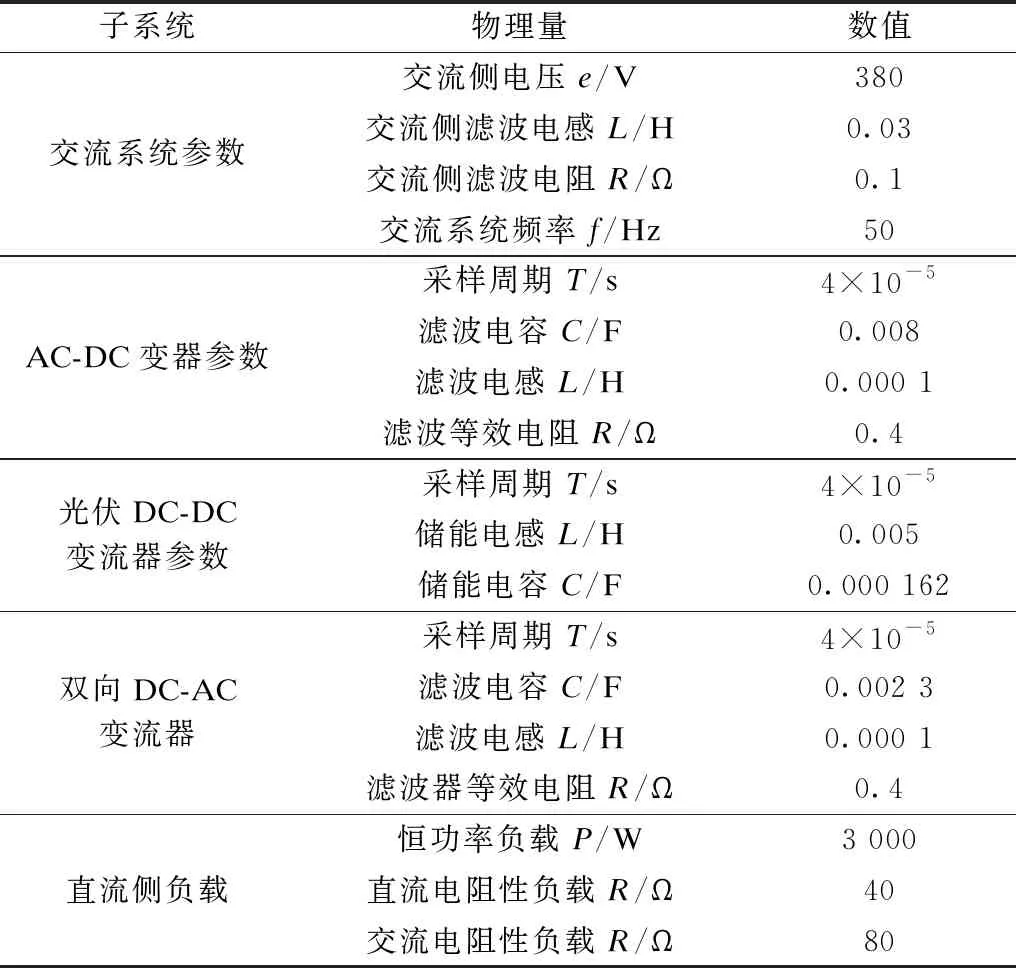
表1 系统参数Tab.1 System parameters
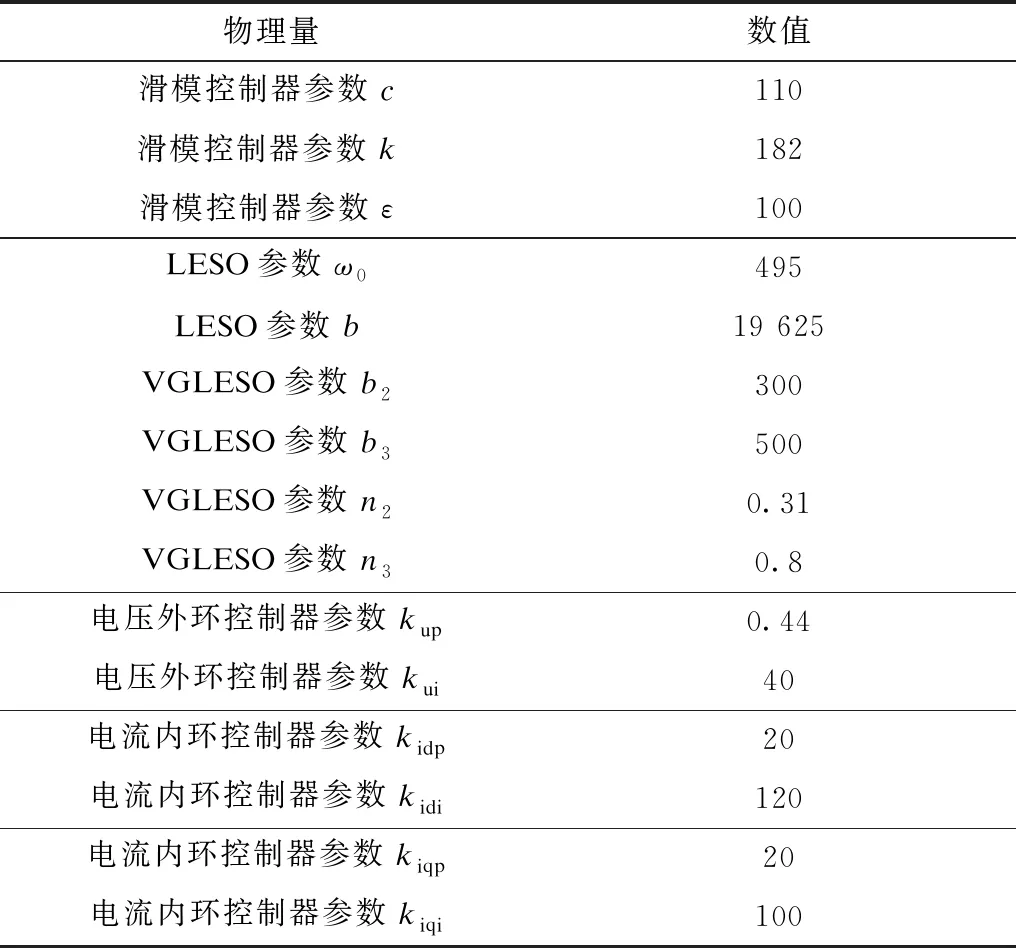
表2 控制系统参数Tab.2 Control system parameters
5.1 VGLESO对系统状态变量的跟踪性能分析
图5为VGLESO和传统高增益LESO对系统状态变量Udc的跟踪曲线图。从图中可以看出,在保证相同跟踪精度的前提下,VGLESO有效地削弱了高增益LESO的初始峰值现象。
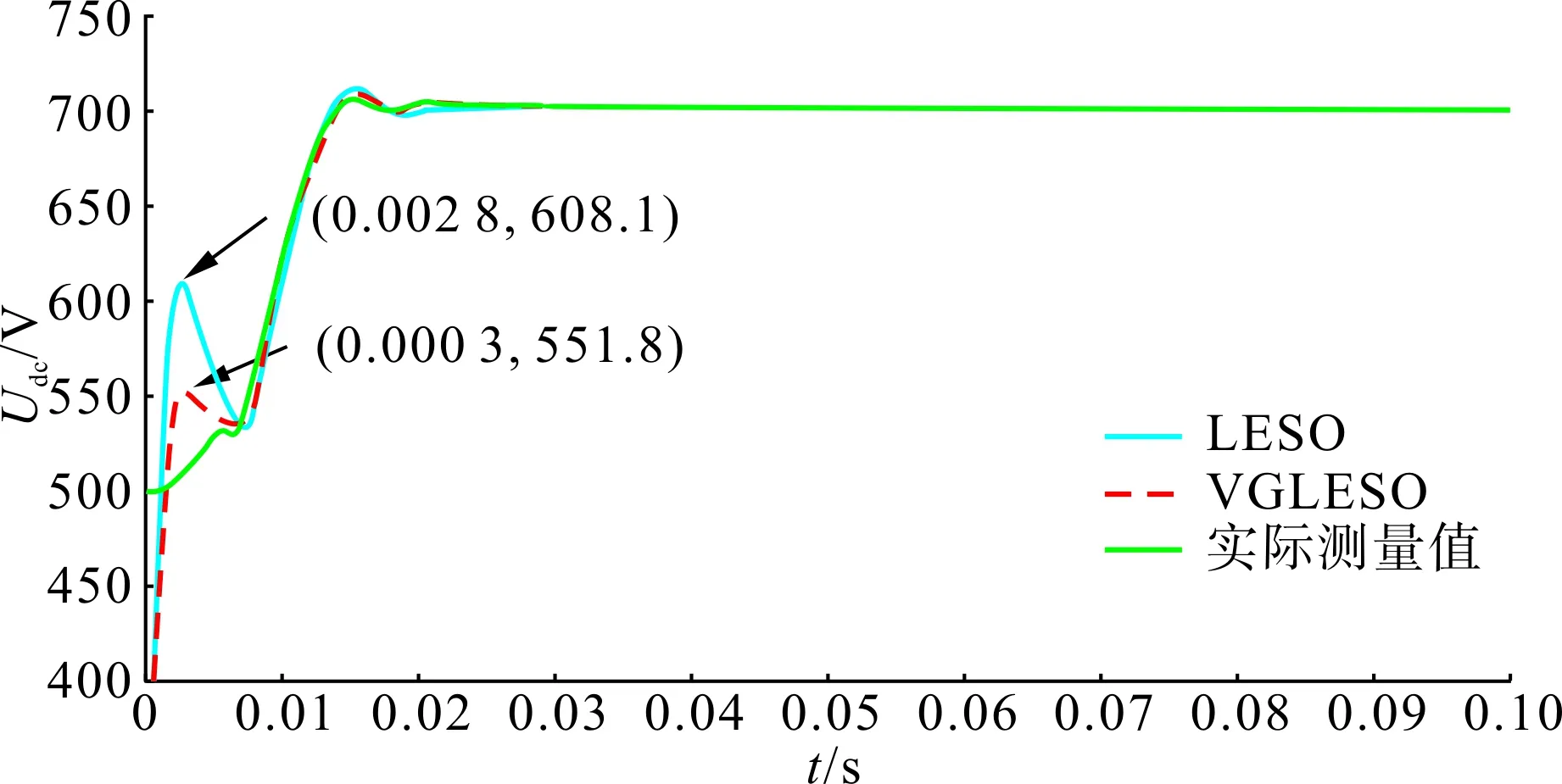
图5 状态变量x1 (Udc)的跟踪曲线Fig.5 Tracking curves of state variablex1 (Udc)


5.2 滑模自抗扰控制器的控制性能分析
为了验证滑模自抗扰控制器的控制效果,进行了如下仿真实验。
1)工况一:系统在正常运行的前提下,在0.25 s的时候直流侧电阻性负载突然减半。
2)工况二:系统在正常运行的前提下,在0.45 s的时候直流侧恒功率负载突然减半。
3)工况三:系统在正常运行的前提下,在0.6 s的时候a相电压突然发生跌落,持续时间为0.1 s。

图6 状态变量x2 (ic)的跟踪曲线Fig.6 Tracking curve of state variablex2 (ic)
在上述工况下,电压外环分别采用了PI控制策略,传统滑模自抗扰控制策略以及变增益滑模自抗扰控制策略。3种控制策略下的直流配电网母线电压波动情况图如图7所示。

图7 母线电压总体波动情况Fig.7 Overall fluctuation of bus voltage
下面将从以下几个方面详细介绍3种控制策略的优缺点。
图8为双向AC-DC变流器采用不同控制策略启动时的母线电压波形图。从图中可知,一方面,两种控制器控制下的系统上升时间是相同的,但二者的超调量却相差甚大,其中,变增益滑模自抗扰控制器控制下的系统的超调量几乎为0,而传统滑模自抗扰控制器控制下的系统的超调量为3.2%。另一方面,变增益滑模自抗扰控制器控制下的系统,当母线电压到达额定电压700 V时,就基本维持在额定电压附近,几乎无暂态过程,而传统滑模自抗扰控制器控制下的系统还需要经过一系列的过渡过程才能维持在额定电压附近。综上所述,变增益滑模自抗扰控制器的启动性能要优于传统滑模自抗扰控制器。
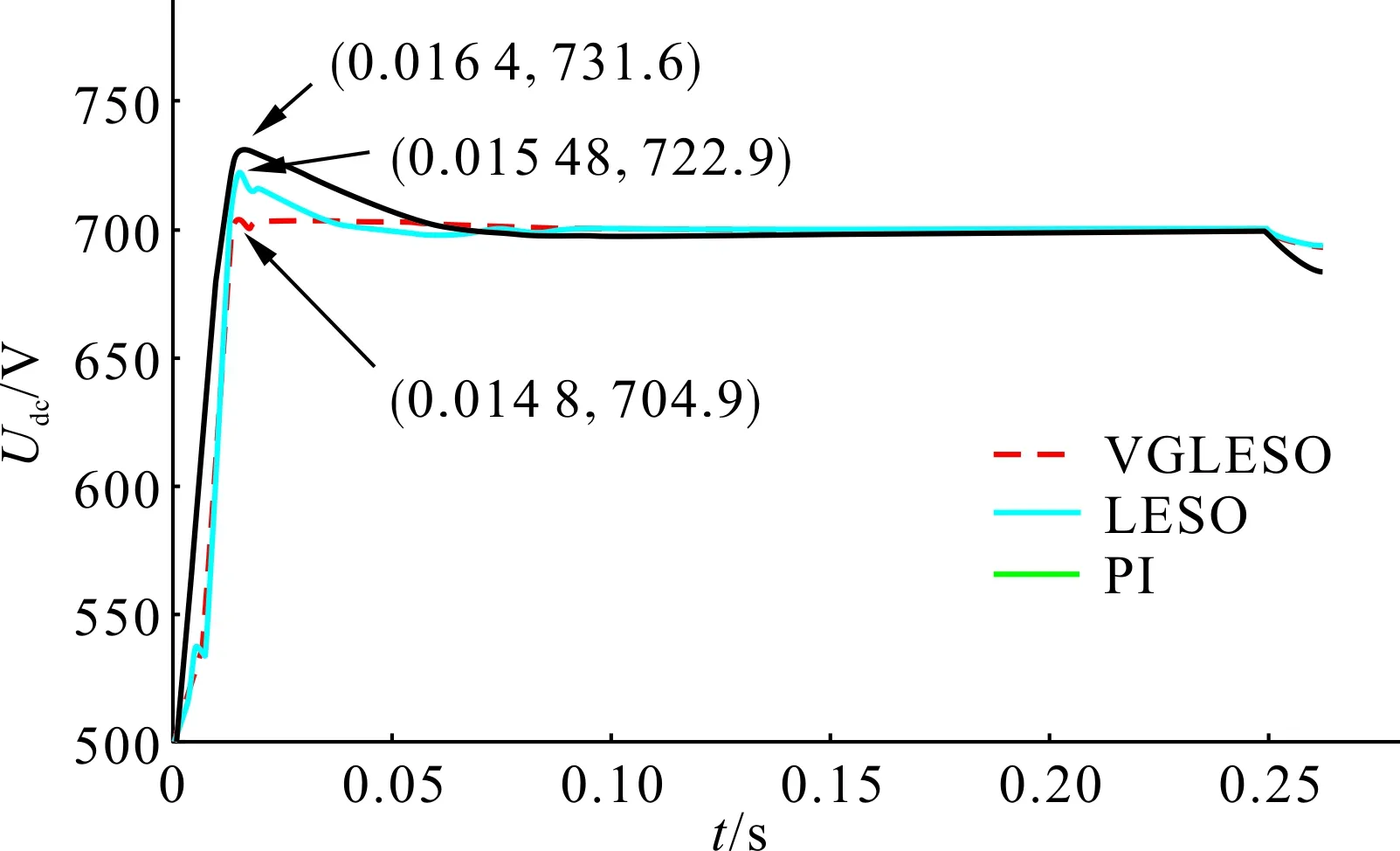
图8 启动特性Fig.8 Starting characteristics
当负载电流突然减小时,由于电容两端的电压不能突变,所以直流侧电流idc的变化要滞后于负载电流iL的变化,因此流过电容两端的电流ic要减小。根据式(33)可知母线电压要发生跌落。
(33)
式中:t0为电容充放电时刻;Δic为电容两端电流变化量。
从图9和图10可知,变增益滑模自抗扰控制器的控制性能这时已经和传统高增益滑模自抗扰控制器的控制效果保持一致,两者的过渡过程时间和电压振荡范围都要小于PI控制策略。因此变增益滑模自抗扰控制策略在荷扰动下能够很好的抑制直流母线电压波动,缩短系统的过渡过程时间。

图9 电阻性负载突然减半母线电压波动图Fig.9 Bus voltage fluctuation diagram with resistance load suddenly halved
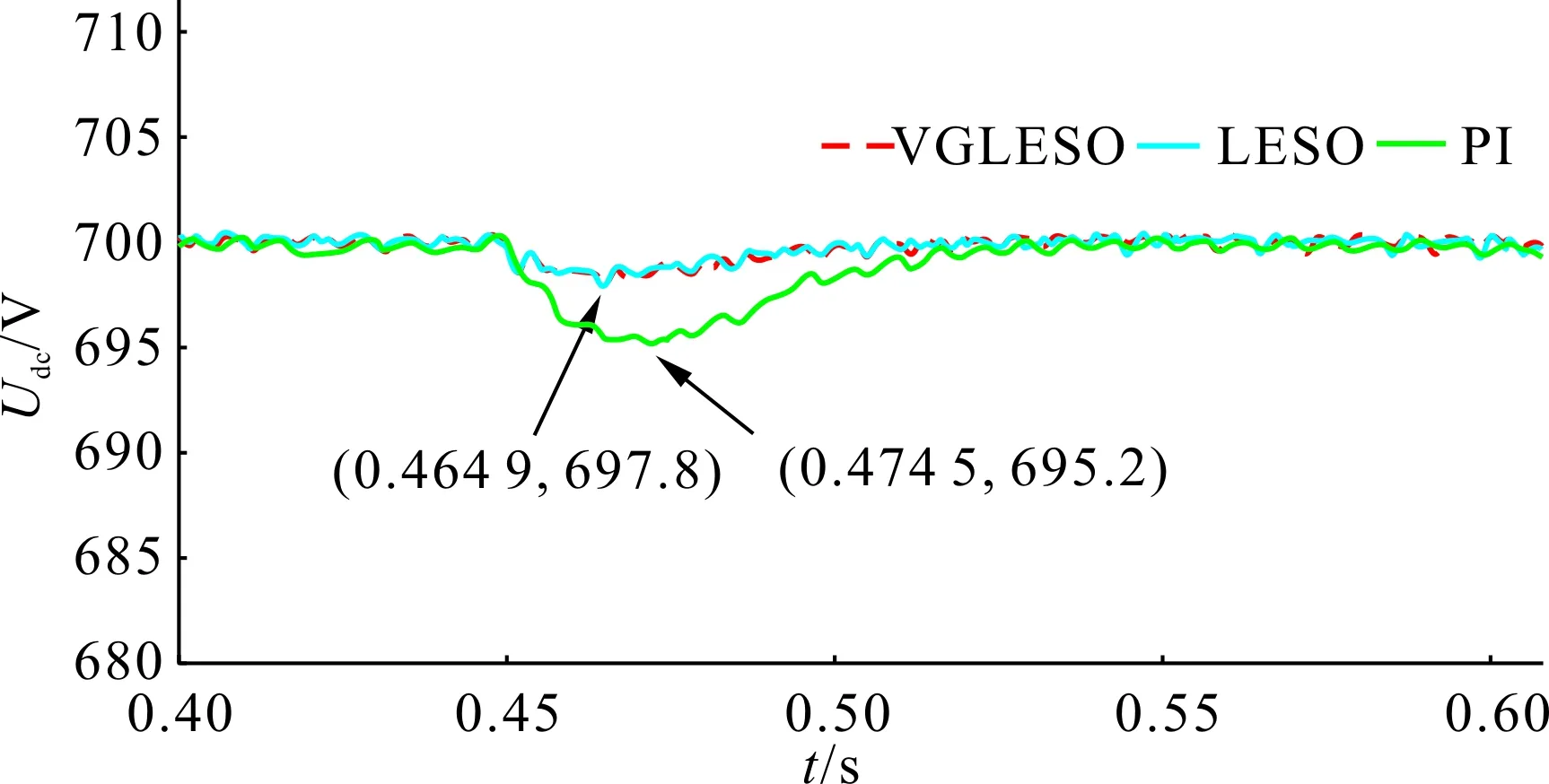
图10 恒功率性负载突然减半母线电压波动图Fig.10 Bus voltage fluctuation diagram of with constant power rate load suddenly halved
从图11和12可知,当三相系统不平衡时,变增益滑模自抗扰控制器的电压波动更小;当三相系统重新平衡时,滑模自抗扰控制器的超调和快速性均优于PI控制器。因此变增益滑模自抗扰控制策略在交流电网发生不平衡时可以很好地稳定公共直流母线的电压,保证系统能够以较快的速度恢复稳定。
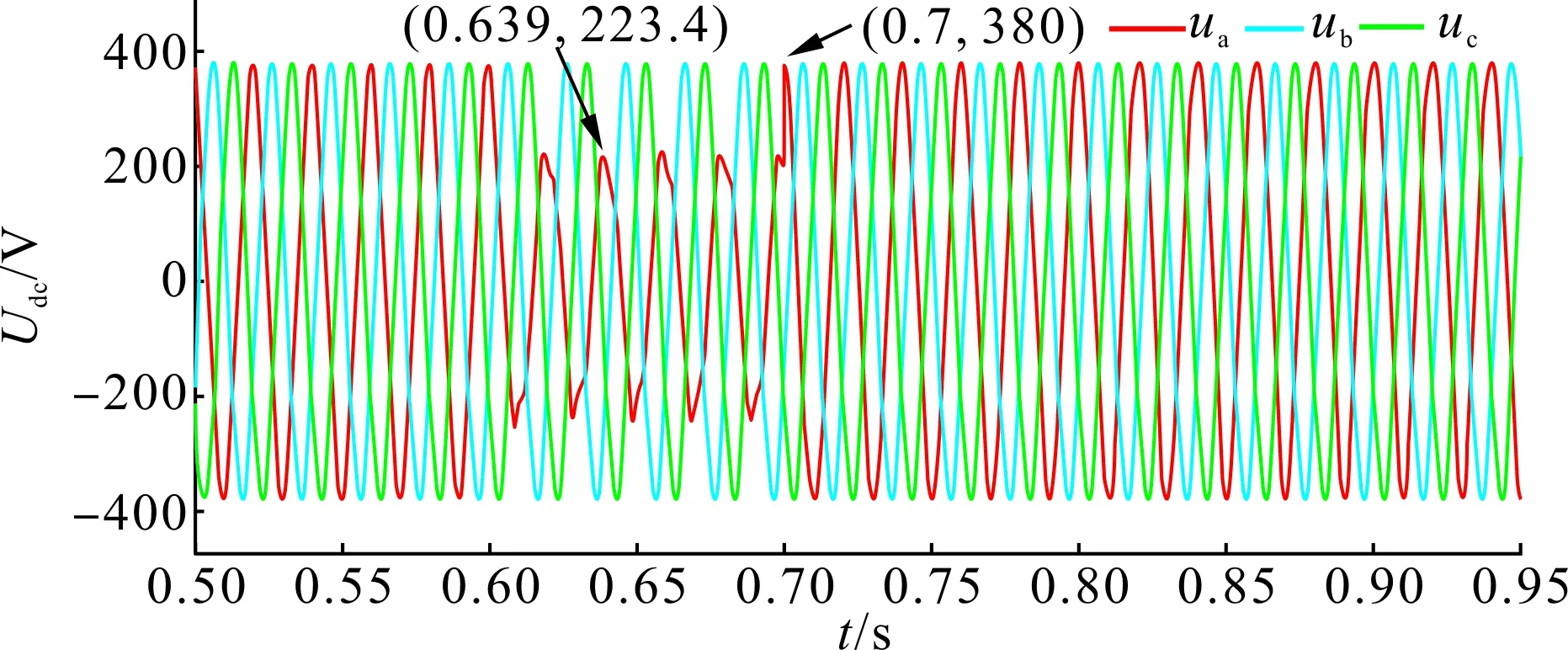
图11 三相电压波形Fig.11 Three-phase voltage waveforms
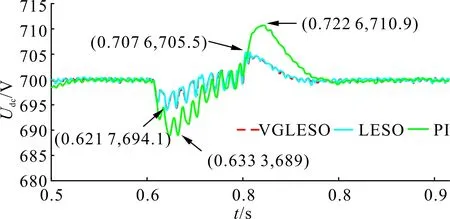
图12 三相电压不平衡时的母线电压Fig.12 Bus voltage in case of three-phase voltage imbalance
6 结论
本文针对直流配电网AC-DC变换器的数学模型,考虑到高增益LESO存在的初始峰值问题,设计了一种变增益LESO来对系统的状态变量和总扰动进行跟踪估计,证明了变增益LESO的收敛性。在此基础上,进一步结合滑模理论设计了变增益滑模自抗扰控制律,并证明了系统的稳定性。
仿真结果表明,与高增益LESO相比,本文设计的变增益LESO不仅能够有效地削弱初值峰化现象及影响,而且还能保持高增益LESO的高观测精度。基于变增益的滑模自抗扰控制器能够在不需要额外电流传感器器的情况下就能够很好地抑制直流配电网各种工况下的扰动,提高了控制系统的动态品质和配电网系统的供电可靠性。同时,由于变增益滑模自抗扰控制器的设计不依赖于系统的结构和参数,使得其具有较强的鲁棒性和可移植性,特别是针对难以建立精确数学模型的非线性系统。

