纳米改性聚丙烯复合绝缘材料性能研究Ⅰ
——在交流电场下的击穿特性
张楚岩,杨松澎,廖一帆,张福增,王国利,王黎明,刘慧芳,徐惠勇
(1.中国地质大学(北京)信息工程学院,北京100083;2. 重庆大学电气工程学院,重庆400044;3.南方电网电力科学研究院,广州510663;4. 清华大学深圳国际研究生院,广东 深圳518055)
0 引言
随着材料科学的不断进步,相比传统绝缘材料,以高分子聚合物为代表的复合绝缘材料的优势逐步显现,并在近些年内得到了快速发展和广泛应用[1 - 3]。然而,电网电压等级的升高、极端气候现象的频发、复杂多变的工作环境还是给这些电介质材料的使用寿命带来了极大的挑战,采用等离子体处理等手段以改善绝缘材料使用性能的研究也取得了良好的进展[4 - 6]。然而,不论是外绝缘还是内绝缘,高分子复合绝缘材料在高电场强度条件下的击穿仍是其应用中需要注意的一大问题[7 - 9],需要进一步的理论与实验研究,找到提升其性能的方法,为工程应用提供支持,避免事故发生。
大量研究表明,添加纳米颗粒物能够有效提升高分子复合电介质材料的性能[10]。经过纳米改性后,不仅材料的电气性能有了提高,其机械性能以及热老化性能也要比普通的聚合物材料更为优异[11 - 12]。
聚丙烯(polypropylene,PP)作为一种高分子聚合物电介质,与聚乙烯等其他聚合物一样在电力系统的应用中也有着一席之地[13 - 14]。薄膜形式的聚丙烯作为一种介电媒质多被用于高性能脉冲发生器及低损耗射频电容器中[15 - 16]。此外,由于具有相对较高的熔点,聚丙烯作为绝缘媒质还被应用于大容量的电力电缆中[17 - 19]。
目前已有很多研究关注纳米添加对聚丙烯和环氧树脂材料性能尤其是电气与力学性能的改进[20 - 22]。其中,有研究在低电压条件下评估了聚丙烯材料的介电谱[23 - 24]。有学者通过实验研究了聚丙烯及其纳米复合物中的电荷分布[25 - 26]。研究发现当纳米黏土颗粒添加到聚丙烯中时,可以改善材料中的电荷分布特性。从而可以合理推断:纳米材料的添加可以同时改善聚丙烯的电气击穿特性。另有学者将纳米粘土颗粒添加至环氧树脂中进行力学试验,发现经纳米改性后,材料的冲击强度和弯曲强度都得到了大幅提升[27 - 28]。
然而,目前以天然蒙脱石作为纳米添加物对聚丙烯材料进行改性后,材料的电气击穿及电流密度特性的试验数据较少,值得做进一步补充研究。
综上所述,本文的研究工作关注纳米颗粒(天然蒙脱石)添加对聚丙烯材料的击穿场强、电流密度与电场强度间的函数关系的影响,从而评估和比较不同添加比重条件下材料电气性能的变化,期望为改善聚丙烯绝缘材料的综合性能提供基础数据和研究思路,使其得到更好的应用。
1 实验试品及实验方法
1.1 材料
本文采用了多组聚丙烯(PP)复合绝缘薄膜试品开展实验。其中,对照组使用加拿大Basell公司生产的等规聚丙烯绝缘薄膜(Profax HL- 451H),未经纳米颗粒添加。其余组均经天然纳米黏土颗粒进行了一定程度的改性,天然纳米粘土的成分是蒙脱石,也称为绿帘石或Cloisite®20A,其化学式为:[Al1.67Mg0.33(Na0.33)]Si4O10(OH)2。纳米成分添加比重若过低(小于1%),不利于发挥纳米改性的作用;添加比例若过高,则可能影响材料本身的一些良好属性,或者降低材料的其他性能比如机械特性。因此,本文选择的纳米颗粒物添加比重范围为1%~10%,在开展本文实验研究时,选择添加比重分别为2%和6%的同等尺寸聚丙烯薄膜试品与对照组进行对比实验,且所有纳米复合薄膜中的基底材料均一致。3组试品的组成成分如表1所示。
实验中采用的聚丙烯复合绝缘薄膜试品均被切割成边长50 mm的正方形,薄膜厚度为(140±5%)μm。薄膜厚度的测量采用刻度为10 μm的千分尺。
1.2 实验设备
本实验所使用的主要设备包括一个不锈钢实验罐体、试验变压器以及电气参数测量设备,实验布置及接线图如图1所示。
其中,平行配置的电极板是由不锈钢制作,与实验材料接触的表面为直径33 mm的圆形,由于所用聚合物绝缘材料薄膜的厚度远远小于电极的尺寸,因此试品上的电场分布可近似为一均匀电场。为了减少边缘效应以及金属部件不必要的电晕放电,整个实验罐体内充满绝缘油(变压器油),实验时,电极与聚合物绝缘薄膜均浸润其中。
实验电源为一容量5 kVA、频率为60 Hz的试验变压器,高压的测量使用电容式分压器。同时,实验通过一个串联在低压端电极和接地之间的(1±0.01%) kΩ的无感电阻来进行聚合物绝缘薄膜体电流密度的测量。试验中使用的都是带电屏蔽的电缆,因此可以有效避免电磁干扰。通过读取电阻两端的电压值,即可获得实验电流。实验设备如图2所示。
1.3 实验流程
实验的操作流程如下:首先按图1所述方式完成实验各组成部分的布置,然后采用2种不同的升压方法从0 kV开始升压直至试品发生击穿,并记录相关实验数据。2种不同加压方式的区别在于升压速率不同,如图3所示。一种以较低的升压速率(约为170 V/s)进行阶跃式升压至试片击穿失效,;另一种以较高的升压速率(约为1 490 V/s)进行直线式升压直至试片击穿失效。选择这2种升压速率的原因是:即便是在170 V/s速率的条件下,薄膜试品由加压到击穿的时间都在3 min以内,相比长期的运行,可认为试品的击穿属于电击穿;因此,在3 min以内完成试品的击穿,以实验电源升压操作方便为宜,选择了本文的2种不同升压速率,1 490 V/s是实验电源可操作的最快升压速率,而为与之区别,将升压速率降低至约1/10,经多次计算,实际升压速率为170 V/s。最后根据所记录的实验数据,绘制试品的“电流密度-场强”曲线。
每组采用5片试品进行实验并取其平均值,采用阶跃式升压时,每次升压采集10~12个数据点。

图3 两种不同升压方式Fig.3 Two different rise-voltage methods
2 结果与分析
2.1 击穿场强特性
根据实验的布置情况,试品所承受的电场几乎为均匀分布,其击穿场强可以由式(1)计算。
(1)
式中:Eb为击穿电场强度;Ub为击穿电压;d为试品的厚度。
图4给出了在2种不同升压方法下获得的聚丙烯复合绝缘材料击穿场强Eb随着纳米颗粒添加比例不同的变化曲线。分析如下。

图4 聚丙烯击穿场强随纳米黏土添加比重的变化Fig.4 Breakdown electric field intensity VS concentration of nanoclay in PP
1)在阶跃式升压方法下,未进行纳米颗粒添加的聚丙烯(PP)薄膜的平均击穿场强约为109.91 kV/mm,在阶跃式升压方法下的标准偏差约为4.05 kV/mm。随着纳米颗粒添加比例的提高,击穿场强有所提高,添加比例2%和6%的第2和第3组试品其击穿场强分别比未添加的第1组试品高出4.59%和5.54%。从数据同时可以得到,添加比例2%的第2组试品其击穿场强与添加比例6%的第3组试品的Eb相差仅为0.9%。因此,在提升聚合物材料电气性能的基础上考虑材料改性的经济性,纳米成分添加的比例不宜太高,以本文的实验为例,添加比例为2%即可实现性能的明显提升。
2)在直线式升压方法下,未进行纳米颗粒添加的聚丙烯(PP)薄膜的平均击穿场强约为122.07 kV/mm,这要比采用阶跃式升压方法获得的击穿场强值高出11.06%。同时,在直线式升压方法条件下,添加比例2%和6%的试品其击穿场强分别比未添加的试品高7.95%和9.45%。与采用阶跃式升压方法所得到的结论相似,添加比例6%试品的Eb仅比添加比例2%试品的Eb高出约1%。
2.2 电流密度特性
本文同时研究了随着纳米颗粒添加比例的变化复合绝缘试品的电流密度与所受电场强度之间的关系。根据电介质的基本性质,正弦稳态条件下电介质的电流由两部分组成,其一为基于电荷运动形成的传导电流,大小主要受电介质电导率的影响;其二为基于电通量密度变化产生的位移电流,大小主要受电介质介电常数的影响。传导电流计算公式为:
(2)
式中:IO为传导电流;JO为传导电流密度;σ为电导率;E为电场强度;S为截面大小。由于本试验使用的聚丙烯复合绝缘材料的电导率仅在10-18S/m的数量级,故电导率σ很小,从而使得计算得到的传导电流非常小,故可以忽略。
因此,材料的体电流密度主要由介电常数来支配。实验测量得到的电流值基本上代表了电介质位移电流的大小。图5给出了3组试品所测量得到的电流密度J与电场强度E之间的关系,即“J-E”变化曲线。每个数据点的误差绝对值在0.5%~3%内。
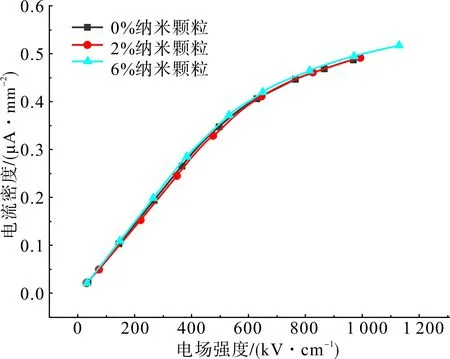
图5 电流密度与场强间的变化关系Fig.5 Variation of current-density with electric filed intensity
从图5中可以看出,电流密度随着材料所承受电场强度的增加而增加,并在起始阶段呈现出类似线性关系的陡峭增长趋势。随着电场强度的进一步增长,当场强超过某一数值之后,电流密度虽然仍继续增大但不再是线性的,并出现了饱和的趋势。对于0、2%以及6%不同纳米颗粒添加比例的试品来说,电流密度增长趋势出现变化的场强值分别约为490 kV/cm、500 kV/cm以及520 kV/cm。本文中将这一场强定义为“临界变化电场强度(Ec)”,它表征着使聚合物绝缘材料电介质性质发生明显改变所需的电场强度值。
同时,根据麦克斯韦方程,正弦交变稳态电磁场中位移电流密度J与角频率ω以及电位移D有着如下关系:
J=ωD=ωεE=ωε0εrE
(3)
于是可以推导出相对介电常数εr与电场强度E之间的关系如式(4)所示。
(4)
式中:ε0=8.85×10-12F/m;角频率ω为已知可计算的,其计算公式如下:
ω=2πf
(5)
根据实验测量得到的电流值(“J-E”关系变化曲线),经过计算,可绘制3组试品的“εr-E”关系变化曲线如图6所示。

图6 相对介电常数与场强间的变化关系Fig.6 Relative permittivity as a function of electric field intensity
从图6中可以看出,未添加纳米颗粒以及添加比例为2%和6%的聚丙烯复合绝缘薄膜的相对介电常数分别约为2.23、2.17和2.27。当材料所承受的场强未达到临界变化场强时,其相对介电常数基本不发生变化。当试品上的场强值超过临界变化场强并持续增加至击穿场强值时,材料的相对介电常数几乎呈线性状态迅速下降,此时,电介质材料实际上已经发生了化学老化。需要注意的是,不同成分的聚合物其相对介电常数是不同的,下降程度可能会有差异但趋势是一致的。根据实验结果,在击穿场强值达到前,3组试品的相对介电常数分别下降到约1.55、1.50和1.38。
3 讨论
3.1 击穿机理的探讨
在交流电压下,聚合物的分子形态对其击穿特性是有一定影响的。聚丙烯材料的击穿通常发生在分子密度较低的地方。有研究表明[9],高分子聚合物材料最高的击穿电压点是高分子材料的晶球密集区,而最低的击穿电压则发生在晶球间的低密度区域。因此,通过纳米颗粒的添加形成纳米复合材料并以此提升聚丙烯材料击穿强度的基本原理是纳米颗粒填充了那些低密度的区域,补强了材料的电气特性。
此外,从本文的实验研究结果可以看出,随着纳米成分添加比例的增加,材料电气特性的提升是非线性的,具有饱和效应,如本文的实验:当添加比例由2%提升至6%时,聚丙烯复合绝缘材料的电气特性未再有明显提升。实际上,对于纳米改性的聚合物绝缘材料来说,曾有研究推荐过较为理想的添加比例[8],这是因为在某种添加比例下,复合材料中的纯号电荷已经能够被大幅减少。
3.2 不同升压方式的对比
不同的升压方法意味着升压速率的不同,对于阶跃式升压来说,其升压速率约为170 V/s,而直线式升压的速率约为1 490 V/s。对比图4的曲线可以看出,直线式升压所获得的材料击穿场强要明显高于阶跃式升压法的结果。产生这种差异的原因如下。
虽然电离的过程确实很快,但固体电介质分子被电离,化学键被打开需要足够的能量,在升压速度很快时,这种能量几乎完全由电场提供,因此场强要足够高才能击穿。升压速度较低时,能量大部分由电场直接提供,少部分由电流产生的热效应提供,所以击穿场强要比高速升压时低一些,但差距不大。电介质发生击穿所需能量可以是叠加的,升压速度越快,从加压到击穿作用时间越短。试验发现,两种加压速率下,电场作用时间确实有差异,但这种差异不大,不影响对结果的分析,最终都实现击穿。
未来计划在恒压下研究材料的老化击穿特性。因为在电热复合物理场的作用下,与在常温下直接升压时的电击穿不同,材料绝缘的破坏通常是由于热击穿所导致的。
3.3 极化现象的影响
图5中电流密度的饱和趋势可用电介质的净极化来解释。根据麦克斯韦的电磁场理论可知,电位移与电介质材料的净极化成正比。因此随着材料所受电场强度的增加,电介质材料内的极化程度呈现几乎线性的增加,从而导致位移电流密度的线性增加。同时,由于材料的相对介电常数与极化直接相关,相对介电常数也在电场强度超过临界变化场强前保持常量。而当电场强度超过某一个值时,位移电流虽然会继续增加,但由于净极化的减少其增加趋势将变缓,于是导致了材料体电流密度的饱和趋势,同时净极化的减少也使得材料相对介电常数的急剧下降。该过程可用式(6)表述。
D=εE=ε0εrE=ε0(1+χe)E=ε0E+P
(6)
其中,由于ε0的数值极小,使得极化强度P几乎可代表电介质的电位移D。
后续的研究工作将关注纳米改性后聚合物绝缘材料的老化特性以及当材料被应用在电容器或电力线缆中时,如何对其工程使用寿命进行合理预测。
4 结论
本文对经纳米改性后聚丙烯复合绝缘材料的电气特性进行了一系列的实验研究,获得的主要结论如下。
1)随着纳米成分添加比例的增加,聚丙烯复合绝缘材料的击穿电场强度逐渐提高,但这种提高并非是线性的,具有饱和效应。在阶跃式升压法条件下,添加比例2%和6%的试品其击穿场强分别比未添加的试品高4.59%和5.54%;而在直线式升压法条件下,提高比例分别为7.95%和9.45%。
2)实验测量所得电流代表了电介质材料的位移电流密度。随着所施加电压的升高,聚丙烯复合绝缘材料的体电流密度呈现出先线性增加再非线性增加的趋势,本文将趋势发生变化时的电场强度定义为“临界变化场强”,可表征聚合物绝缘材料电介质性质发生明显改变所需的电场强度值。
3)随着施加电场强度的增加,当场强超过临界变化场强时,聚丙烯绝缘材料的相对介电常数也将发生明显降低,这是由于材料本身发生了化学反应。本文所用3组主要试品在加压前的相对介电常数分别约为2.23、2.17和2.27,而在试品击穿前,其相对介电常数分别下降到1.55、1.50和1.38。
4)纳米改性确实可明显提升聚丙烯绝缘材料的电气性能,但是其是否会影响材料的其他性能仍值得进一步的研究。同时,纳米成分最佳的添加比例需要通过更多的样本试品来确定,以便使其更好地服务于工程。
未来,针对纳米改性对聚丙烯薄膜在电场和温度场共同作用下的老化失效机理及寿命的影响将在未来的研究工作中持续关注。
5 志谢
感谢美国凯特林大学电气与计算机工程学院(Electrical & Computer Engineering Department of Kettering University)的Huseyin R. Hiziroglu教授为本实验提供条件并指导实验研究。本文的研究工作受中央高校基本科研业务费项目和特高压工程技术(广州、昆明)国家工程实验室开放基金项目的支持,在此表示感谢。

