数字电路设计中的化简方法

李音 薛娓娓

（延安大学西安创新学院 陕西省西安市 710100）

1 数字逻辑电路中学习化简的必要性

在数字电子技术这门课程中，在开始的逻辑代数基础章节中，学习完数制、码制、逻辑代数的基本运算之后就要进行公式法化简与卡诺图化简的内容了，作为基础内容存在于第一章节，虽然是基础内容，但是却是数字电路设计里面的一个主要部分，它奠定了逻辑电路设计思路的基础。在这部分内容的讲述中，主要要跟学生说清楚、讲明白为什么要进行化简，目标是什么样的。化简是为了得到最简式，要根据最简式设计电路，这样设计出来的电路才是最简单的。

2 公式法化简

2.1 公式定理两种处理方案

在利用公式法化简之前，首先要对所有的基本公式、常用公式、基本定理进行学习，学习这部分内容时要进行分类学习，在逻辑代数中，有些公式是与普通代数是一样的，很容易理解，例如：0•A=0，0+A=A，AB=BA，A+B=B+A，因为这些完全符合普通代数的乘法和加法。但是也有一些是很容易弄错的，例如，A•A=A , A+A=A，1+A=A，这些就和普通代数有着很大的区别，所以要提醒学生，在这个部分的学习过程中，必须注意与普通代数之间的区别，要提醒学生，逻辑代数只有：”0”和”1”，这样比较好理解，提醒学生逻辑与和逻辑或的特点，0 与任何值等于0，1 或任何值等于1。另外有些定理比较好推导，和普通代数一样例如A+AB=A，这种不需要记忆，现场推导出来就可以使用。但也有一些不易于推导，例如还有多余项定理这种，就需要学生熟练，最好直接记下来，直接使用。

2.2 公式法化简的思路

公式法化简的思路是最终得到的化简式中项越少越好，每个项里面变量越少越好。这里只针对与或式。

上面这道例题属于公式法化简的一种典型例题，这种使用公式法化简最好，这个做法现在最后两项中，提取出，剩下1+A，1 或任何值等于1，所以接着最后在表达式里面找A 与，有A 的项直接可以消去，有的项直接消去就可以。

2.3 需要注意的问题

（1）在利用公式法进行化简时，逻辑代数中只有逻辑与和逻辑或，没有除法也没有减法，例如AB=AC,即B=C。还有A+B=A+C,即B=C，这两个式子都是错误命题，前一个用了除法，两边同时除以A，才可以得到B=C，第二个用了减法，两边同时减去A，得到B=C，可以给学生举例像第一个式子中A=0，B=0,C=1所以AB=AC 成立，但是B 不等于C，第二个式子中A=1，B=0，C=1 所以A+B=A+C 成立，但是B 不等于C。

（2）公式法化简存在的问题就是有时候没有办法很快的确定，我们得到的式子是不是最简式，那么公式法化简就可以弥补这样的缺陷。

3 卡诺图化简

3.1 卡诺图化简的根本依据

这种利用卡诺图化简的依据就是相邻的最小项可以合并，并消去不同的变量，那么我们就需要卡诺图中所有对应的最小项是逻辑相邻的。图1分别为二变量、三变量、四变量所对应的最小项的卡诺图。

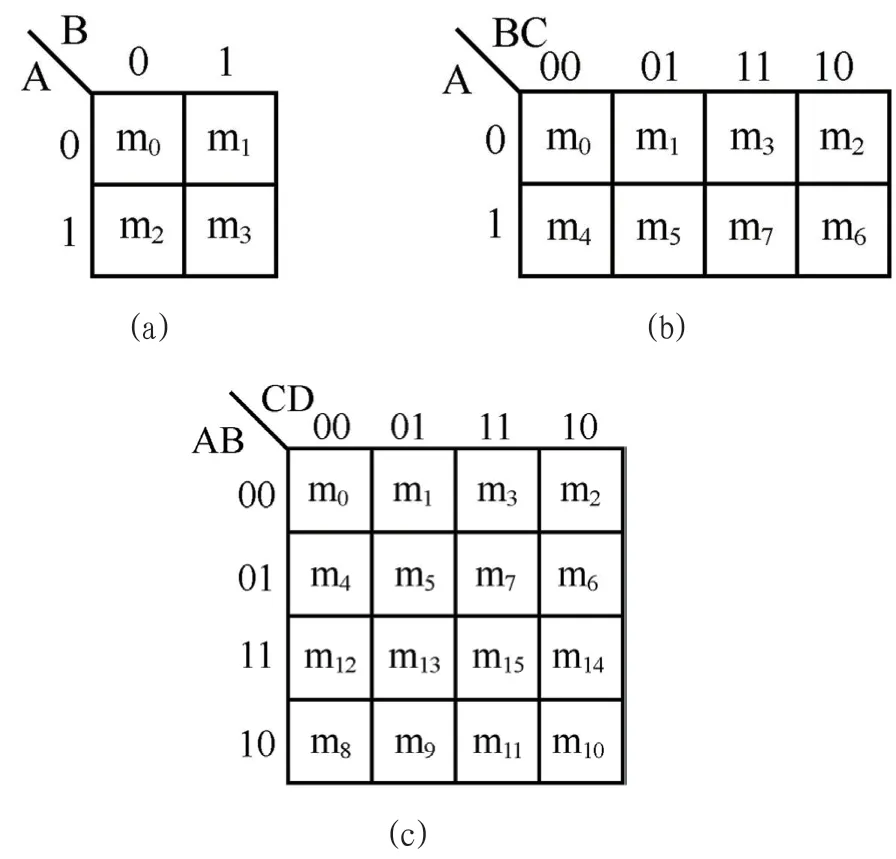
图1：二变量、三变量、四变量所对应的最小项的卡诺图

3.2 卡诺图化简的步骤

（1）如果已知表达式，要求利用卡诺图化简，首先把表达式写成最小项和的式子，注意变量都有哪些，按照缺什么补什么的办法，使每一项都成为最小项。

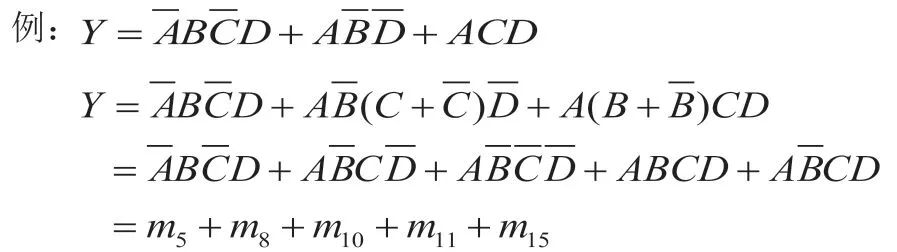
上式中共有三项，可以观察出变量为A、B、C、D 四个变量，第一项已经是最小项，最小项就是要求每个变量都有，而且都是以变量或者反变量的形式出现并且与起来。第二项只有A、B、D 三个变量，缺C，给第二项与上，这样就得到了两项，均为最小项。第三项只有A、C、D 三个变量，缺B，给第二项与上，这样就得到了两项，均为最小项。最后根据每个最小项判断都是哪个最小项，m 的角码是多少，原变量为“1”，反变量为“0”，对应0101 转换成十进制为5，即是m5，对应1010 转换成十进制为10，即是m10，对应，1000 转换成十进制为8，即是m8，对应，1111 转换成十进制为15，即是m15，对应1011 转换成十进制为11，即是m11，这样就得到上面的最终表达式。

（2）“填1”，按照卡诺图中最小项的位置，对应位置填1，得到卡诺图2。

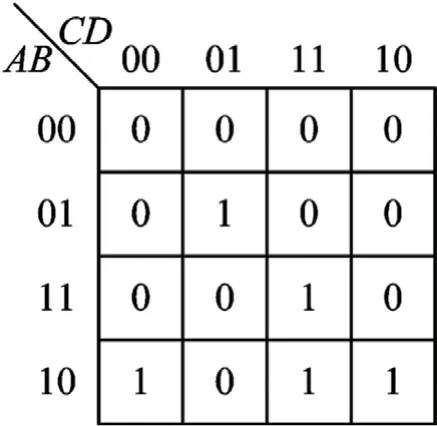
图2：例题1 的卡诺图

“圈圈”，规则：2n（1,2,4,8...）个1 圈起来，1 均是是逻辑相邻的关系，注意以横竖中线对折，重合的部分均是逻辑相邻；圈起来的圈为正方形或长方形，注意边边角角的相邻关系；每个1 都可以被重复圈；每个圈里面至少有一个1 没有被其他圈圈过；注意：圈数越少越好，则对应的项越少，圈越大越好，每项对应的变量数越少。

（3）写表达式。

每个圈对应一个项，最后把所有的项或起来就得到表达式了，方法是留下相同的变量，去掉不同的变量。

3.3 举例分析

例1：

图3中总共圈了两个圈，其中四个1 被重复圈了，左侧四个1 与右侧四个1 是一个圈，注意这个是一个圈，以竖中线折叠具有相邻性，所以是一个圈，对应项为，因为A、B、C、D 值中只有相同值D=0，其他A、B、C 值都不同，0 对应反变量，所以为。对应的下面8 个1 是一个圈，A、B、C、D 值中只有相同值A=1，其他B、C、D 值都不同，1 对应原变量，所以为A。故得到

图3：例题2 的卡诺图

例2：如图4，对卡诺图进行圈1，并写出最简式。

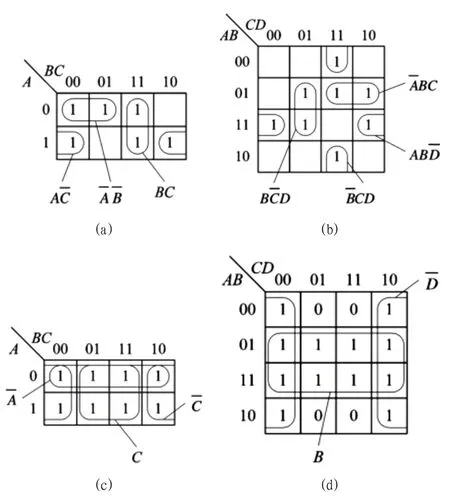
图4：例题3 的卡诺图

图4（a）中有6 个1，四个1 不能圈，圈出来不是正方形，也不是长方形，只能两个1 圈，总共3 个圈，对应的表达式为另外我们应该注意到这个卡诺图还有另一种圈法，但是还是3 个圈，每个圈有两个1，所以就结果来看都是对的，而且电路简易程度是一样的。

图4（b）中有8 个1，只能两个1 圈，总共4 个圈，对应的表达式为另外和图（a）一样，这个卡诺图也还有另一种圈法，但是还是4 个圈，每个圈有两个1。由此可见，有时候我们在进行化简时结果可能不一样，但是都是正确的。

图4（c）中有8 个1，总共3 个圈，四个1 圈，对应的表达式为但是明显这个结果是不对的，可以八个1 圈，通过表达式我们也可以发现有C 也有，相加是等于1 的，那么像这种，所有最小项都存在，加起来是等于1 的。

图4（d）中有12 个1，公用四个1，八个1 圈，总共2 个圈，对应的表达式为

3.4 注意的几点问题

从以上可以看出来，卡诺图圈法不是唯一的，最简式不是唯一的；另外在填1 时，也可以根据表达式直接填1，例如表达式中有A，所有A=1 的格子都填1，像，所有A=1 且B=0 的格子都填1；最后圈1 时要注意边边角角的相邻的1。

4 总结

以上为公式法化简和卡诺图化简需要注意的一些问题，公式法化简适用于变量比较多时使用，由其是多余项定理的使用，但是缺点是无法确定是不是最简式，卡诺图优点是可以根据圈圈确定是最简式，但是存在当变量太多，卡诺图太复杂不易于圈圈的问题。