一道“零点”习题的探究教学
龙明旺 王芳


摘 要:探究式教学容易激起学生的好奇心,并使学生发挥创造力,让学生用自己的思考方式和方法解决问题,切实体会探究带来的成长与进步,有利于学生必备品格和关键能力的培养.本文以一道“零点”习题的教学为例,对探究式教学作了有益尝试,学生达到的高度让人惊叹.
关键词:零点;探究;核心素养
传统的讲授式教学是通过大量的习题讲解,教学生模仿、套用,却不利于培养学生自主发现和提出问题的能力、分析和解决问题的能力,不利于学生核心素养的培养,不利于学生的长远发展.笔者经常会借助一些典型的问题情境,开展探究课堂,激发学生的好奇心,引导学生自主发现,深入思考,积极探究,并总结反思,创新命题,学生能达到的高度让人惊叹,现举一例如下.
1.问题提出
学生已经学习了零点的概念和二次函数根的分布的基础知识,于是,笔者提出了一道思考题:关于x的方程在上有唯一实根,求实数k的取值范围.
这道思考题留给学生回家做一做,第二天课堂一起探究.
2.探究过程
老师先是询问学生,经过昨天的思考和讨论,大家有哪些切入点和转化方向.
生1(方向一):可以用二次函数根的分布.展示过程:
记,则
①解得
②,解得
(课堂上有学生讨论了,有不同的看法)
生2:做的不完整,你怎么知道一定是二次函数?万一怎么办?所以应该分情况讨论.接着,陈述过程:
当时,,解得,不合要求;当时,为二次函数,才是生1所说的情况.
(课堂上还是有部分同学讨论,感觉有不同的理解.)
生3:老师,生2没有考虑边界,因为或也有可能,应该把改成.(课堂有学生说有点道理,但是也有学生感觉不对,提出了异议.)
生4:如图1,这样也满足,但是不符合题目唯一实根的条件.
(课堂上有学生讨论说,生4说的是对的,那怎么处理呢?学生陷入沉思,但是脸上的表情反映内心的迷茫,看来还需要一些点拨)
师:刚才几位同学提出和发现问题,表现得很好.现在这里碰到了难度,
还是讨论不清楚.难在端点怎么处理?那同学们想一想,把和
合在一起讨论,有困难,怎么办?
生5:可以把單独讨论!
师:生5说的非常好.逆向思维,退一步,海阔天空.接下来,如何讨论呢?
生5:可以把或1代入方程,求出另一个根,看是否符合要求.过程如下:
当x=0时,带入方程得,原方程化为,即,解得另一个根,符合要求.
当x=1时,带入方程有,解得,原方程化为,即,解得另一个根,符合要求.
师:生5解得很好.在求另一个根时,除了把k带入原方程,解出另一个根之外,还有没有求另一个根的更简便方法?
生6:(反应很快)可以用韦达定理,过程如下:
①当x=0时,带入方程得,设的另一个根为,由韦达定理有,解得,符合题目要求
②当x=1时,带入方程得即时,设的另一个根为,则由韦达定理可知,解得,符合题目要求.
师:时的情形,为什么不用?
生6:如果用用,这样要么无解或有无数个解,还得通过来确定,这样麻烦多了.
师:生6说的太好了,选择有讲究,细节处理非常到位. (生6喜悦之情溢于言表)本题的答案应该为四大类情况的并集,即.本题如果把闭区间改成是开区间,又如何做?答案还是一样的吗?
(接着学生看前面的讨论过程)
生6:只需在前面的讨论过程稍作修改就可以了.时的情形,把对称轴改成.另外,把当和时的情形,符合题目要求改成不合题目要求就可以了.
画成图形为图2,
故答案应该为
师:生6讲的完全正确,非常好.我们把刚刚几位同学的发言和探究成果做一个总结:
若二次函数在区间上有唯一实根,则分哪些情况讨论?
生7:分三大类讨论:
(1) (2)
(3)由或求出对应的参数,结合韦达定理求出另一个根,看是否符合要求.最后(1)(2)(3)求并集得到最终的答案.(教师黑板上板书成果)
师:生7归纳的很好.当然,开区间也是类似的处理.如果没有告知是二次函数,还要对二次项系数为0时,单独进行讨论.回到原题,除了用根的分布这种代数方法求解,还有什么方法可解?或什么方向可以切入?
生8:可以用几何方法,画图象来求解.具体为:
由得,问题转化为左边的函数与一次函数的交点问题.
师:切入点很好.那左边函数,,还是呢?如何处理?
生8:分情况讨论,画图象,如图3,
由图可知,,k = 0两种情形,两个图像均没有交点,所以k<0
师:生8数形结合得到k<0,做得很好,思路也很自然.同学们还有没有别的方法,能直接看出k<0?
生9:可从函数值域上考虑.由于,所以,,故.
师:生9从代数上来看问题,非常好.两位同学都讲得很对,接下来请生8继续讲一讲的情形又如何处理?
生8:还是画图象.如图4,记,则由图可知,只需满足且,解得.
图4
师:生8的几何方法很直观,也非常简洁,解得很漂亮.掌声鼓励一下.本题是否还有别的解法或切入方向?
生10:能不能参变分离做?由得,已知,故参变分离得:,但到这一步,右边的图象不会画,我做不下去了.
师:同学们考虑右边函数能不能整式部分离?
生10:分母比分子次数高,没办法分离整式部分.
师:生10一语中的,那能不能化归为分母比分子次数高呢?
生10:(反应很快)可以取倒数.
(有同学灵机一动开始动笔尝试,有同学陷入沉思)
生10:,右边的图象还是不会画?
师:当我们遇到困难时,凭空跨越是不现实的,应该努力思考,看是否见过形式类似的问题?如果与某一熟知的问题类似,我们如何利用以前的方法来解决眼前的问题?
生6:可类比以前求过的函数的值域的方法,换元,令x+1=t,则1≤t≤2,x=t-1,于是,把右边函数的图象画出来,数形结合就很好做了.
生10:生6的做法只是求出常数函数与关于t的函数交点个数问题,并不是与关于x的函数y=的交点个数问题?
生6:x+1=t,这说明x与t是一一对应的关系,一个x对应着一个t,反过来,一个t对应着一个x.所以关于t的方程:有多少个解,原方程就有多少个解.
生10:(豁然开朗)有道理.
生9:老师,取倒数后,为什么不直接换元呢?直接换元,跟前面求函数值域一样,乞不是更简单吗?(学生一下子进入兴奋状态)
生9:令x+1=t,则,x=t-1,.
师:刚才几位同学经过思维的碰撞与讨论,把问题讨论的很透,很了不起.接着请同学们画图,看不能把答案做出来?
(学生动笔很快,也有同学好像有所顿悟,似乎在思考能不能更简单一点)
生9:(几分钟后黑板展示解答)由图5可知,,画图6解得.
师:(沿教室查看一圈)我发现只有一半的同学正确画出了图象,很多同学平移时画错了,也有少数几个同学没有画渐进线.能不能避开平移这个步骤,减少平移带来的画图错误?关键是表达式中的减2如何处理?
生:(反应很快)很多学生齐声说:移到等式的左边去.
师:同学们说的非常好,这样,等式就变成,右边变成了双曲函数.
生8:老师,还可以再简单一点,把等式分母中的2也可以去掉,左右两边同乘法以2,从而等式化为.其实,在这里里,就可以把2去分母处理掉,然后换元,更简单.
师:很好的发现,了不起.(班里同学对生8投来钦佩的目光)请同学们再画图,能不能快速做出来?
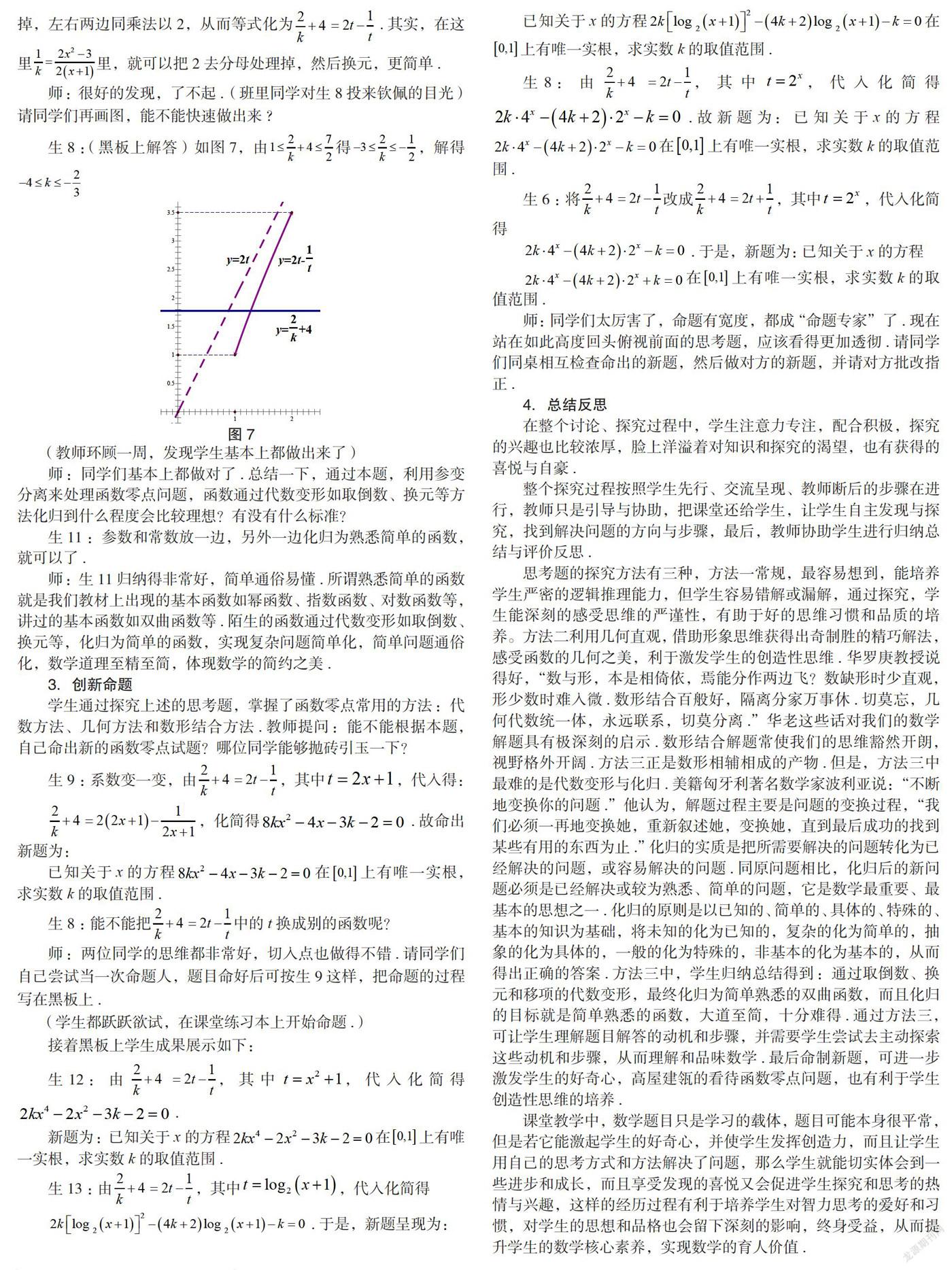
生8:(黑板上解答)如图7,由得,解得
图7
(教师环顾一周,发现学生基本上都做出来了)
师:同学们基本上都做对了.总结一下,通过本题,利用参变分离来处理函数零点问题,函数通过代数变形如取倒数、换元等方法化归到什么程度会比较理想?有没有什么标准?
生11:参数和常数放一边,另外一边化归为熟悉简单的函数,就可以了.
师:生11归纳得非常好,简单通俗易懂.所谓熟悉简单的函数就是我们教材上出现的基本函数如幂函数、指数函数、对数函数等,讲过的基本函数如双曲函数等.陌生的函数通过代数变形如取倒数、换元等,化归为简单的函数,实现复杂问题简单化,简单问题通俗化,数学道理至精至简,体现数学的简约之美.
3.创新命题
学生通过探究上述的思考题,掌握了函数零点常用的方法:代数方法、几何方法和数形结合方法.教师提问:能不能根据本题,自己命出新的函数零点试题?哪位同学能够抛砖引玉一下?
生9:系数变一变,由,其中,代入得:
,化简得.故命出新题为:
已知关于x的方程在上有唯一实根,求实数k的取值范围.
生8:能不能把中的t换成别的函数呢?
师:两位同学的思维都非常好,切入点也做得不错.请同学们自己尝试当一次命题人,题目命好后可按生9这样,把命题的过程写在黑板上.
(学生都跃跃欲试,在课堂练习本上开始命题.)
接着黑板上学生成果展示如下:
生12:由,其中,代入化简得.
新题为:已知关于x的方程在上有唯一实根,求实数k的取值范围.
生13:由,其中,代入化简得
.于是,新题呈现为:
已知关于x的方程在上有唯一实根,求实数k的取值范围.
生8:由,其中,代入化简得.故新题为:已知关于x的方程在上有唯一实根,求实数k的取值范围.
生6:将改成,其中,代入化简得
.于是,新题为:已知关于x的方程
在上有唯一實根,求实数k的取值范围.
师:同学们太厉害了,命题有宽度,都成 “命题专家”了.现在站在如此高度回头俯视前面的思考题,应该看得更加透彻.请同学们同桌相互检查命出的新题,然后做对方的新题,并请对方批改指正.
4.总结反思
在整个讨论、探究过程中,学生注意力专注,配合积极,探究的兴趣也比较浓厚,脸上洋溢着对知识和探究的渴望,也有获得的喜悦与自豪.
整个探究过程按照学生先行、交流呈现、教师断后的步骤在进行,教师只是引导与协助,把课堂还给学生,让学生自主发现与探究,找到解决问题的方向与步骤,最后,教师协助学生进行归纳总结与评价反思.
思考题的探究方法有三种,方法一常规,最容易想到,能培养学生严密的逻辑推理能力,但学生容易错解或漏解,通过探究,学生能深刻的感受思维的严谨性,有助于好的思维习惯和品质的培养。方法二利用几何直观,借助形象思维获得出奇制胜的精巧解法,感受函数的几何之美,利于激发学生的创造性思维. 华罗庚教授说得好,“数与形,本是相倚依,焉能分作两边飞?数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.切莫忘,几何代数统一体,永远联系,切莫分离.”华老这些话对我们的数学解题具有极深刻的启示.数形结合解题常使我们的思维豁然开朗,视野格外开阔.方法三正是数形相辅相成的产物.但是,方法三中最难的是代数变形与化归. 美籍匈牙利著名数学家波利亚说:“不断地变换你的问题.”他认为,解题过程主要是问题的变换过程,“我们必须一再地变换她,重新叙述她,变换她,直到最后成功的找到某些有用的东西为止.” 化归的实质是把所需要解决的问题转化为已经解决的问题,或容易解决的问题.同原问题相比,化归后的新问题必须是已经解决或较为熟悉、简单的问题,它是数学最重要、最基本的思想之一. 化归的原则是以已知的、简单的、具体的、特殊的、基本的知识为基础,将未知的化为已知的,复杂的化为简单的,抽象的化为具体的,一般的化为特殊的,非基本的化为基本的,从而得出正确的答案.方法三中,学生归纳总结得到:通过取倒数、换元和移项的代数变形,最终化归为简单熟悉的双曲函数,而且化归的目标就是简单熟悉的函数,大道至简,十分难得.通过方法三,可让学生理解题目解答的动机和步骤,并需要学生尝试去主动探索这些动机和步骤,从而理解和品味数学.最后命制新题,可进一步激发学生的好奇心,高屋建瓴的看待函数零点问题,也有利于学生创造性思维的培养.
课堂教学中,数学题目只是学习的载体,题目可能本身很平常,但是若它能激起学生的好奇心,并使学生发挥创造力,而且让学生用自己的思考方式和方法解决了问题,那么学生就能切实体会到一些进步和成长,而且享受发现的喜悦又会促进学生探究和思考的热情与兴趣,这样的经历过程有利于培养学生对智力思考的爱好和习惯,对学生的思想和品格也会留下深刻的影响,终身受益,从而提升学生的数学核心素养,实现数学的育人价值.
3712500338260

