考虑港口完全失效风险的班轮运输轴辐式网络设计
王雅宁, 钟 铭, 李明泽
(大连海事大学 交通运输工程学院, 辽宁 大连 116026)
节点失效风险是在通信、交通运输和物流等领域需考虑的一项重要的不确定性因素,根据节点失效程度的不同分为功能性失效和完全性失效,其中:功能性失效是指节点作为枢纽丧失中转能力,仍具有节点的运输能力;完全性失效是指节点的中转能力和运输能力同时丧失。[1]因恶劣天气、疫情、自然灾害和战争等突发事件的发生,导致网络中的节点或仓库丧失运输和中转能力的事件属于节点的完全性失效事件。在轴辐式网络中,枢纽节点承担大量的货流中转任务,一旦发生完全失效事件,将在一定时间段内不能运行,造成网络局部瘫痪。因此,在设计轴辐式网络性时,需考虑节点完全失效的可能性,引入备份策略主动应对网络失效问题,以提高网络的可靠性。例如:AN等[2]建立以成本最小为目标函数的可靠性枢纽模型,考虑备用中心和备用路线主动处理航空网络枢纽中断问题,采用拉格朗日松弛与列生成算法相结合的方法进行求解;AZIZI等[3]研究考虑航空网络中枢纽失效之后,利用备选枢纽进行运输的非线性整数规划模型,采用遗传算法进行求解;TRAN等[4]对每个枢纽设定特定的失效概率,考虑同时可能出现1个或多个枢纽失效的情况,采用禁忌搜索算法对模型进行求解;ROSTAMI等[5]提出2阶段模型,解决枢纽发生故障之后资源重新分配至备选枢纽的问题;胡晶晶等[6]采用变量代换的方法对模型进行线性化求解,采用遗传算法求解大规模算例,在物流应急网络中通过备份枢纽的形式处理枢纽失效问题。
在航运领域,已有研究大多基于港口设施正常运营的假设开展,讨论港口间需求的波动对枢纽选址的影响。例如:钟铭等[7]利用区间集合表示需求不确定,建立混合整数线性规划(Mixed Integer Linear Programming, MLLP)模型,讨论在需求不确定的情况下枢纽选址的问题;MENG等[8]以最小化运输网络设计和集装箱运输的总预期成本为目标,构建需求不确定的混合整数非线性规划(Mixed Integer Nonlinear Programming, MINP)模型;赵宇哲等[9]考虑集装箱需求不确定,利用机会约束规划对模型进行求解。针对突发事件引起港口失效的研究集中在基于复杂网络理论,从港口运营者的角度出发,识别网络中的关键港口方面。例如:宗康等[10]分析网络拓扑结构特性,并在节点随即失效模式下,对不同失效模式节点的测度变化进行仿真;李振福等[11]模拟针对港口的蓄意攻击,分析中国集装箱内河运输网络的结构脆弱性;王诺等[12]对蓄意攻击时全球集装箱网络脆弱性随时间的变化趋势和变化幅度进行分析。这些研究分析了港口失效的可能性,表明海运网络的连通性是由一些枢纽港口的稳定性决定的。
目前,采用备份策略主动应对节点失效的研究集中在航空和通信网络领域,在海运网络中,对港口失效的研究主要基于复杂理论讨论港口的脆弱性,很少在网络设计阶段考虑港口失效的模型。因此,本文从班轮公司的角度出发,基于传统枢纽选址模型,考虑网络中港口的不确定性,针对枢纽港在发生完全失效事件后丧失运输货物能力的问题,结合备份策略,引入备选枢纽港口变量,设计可靠的轴辐式选址模型,主动应对枢纽港口失效对轴辐式网络的影响。同时,考虑网络中的风险成本,提高班轮公司应对风险的能力。
1 考虑备选枢纽的选址模型
1.1 问题描述
轴辐式网络可根据港口配置方式的不同分为单分配航运网络和多分配航运网络2种。在单分配轴辐式网络中,枢纽港承担网络中集装箱流转运的任务,每个支线港口只能与1个枢纽港口相连通,且支线港口的货物必须在与其相连通的枢纽港口中转。
基于这种特殊的网络结构,形成以1个或几个大型枢纽港口为中心,多个共同腹地或共同部分腹地的支线港分布的区域港口群。作为转运中心,一旦该区域内的枢纽港口无法正常运营,将导致部分或整个区域内运输网络崩溃。综上所述,本文基于传统枢纽选址模型建立一种考虑备选枢纽的整数规划模型,在规划期设定枢纽港口存在失效的可能性,为枢纽港提前规划发生失效事件时的备选枢纽与集装箱重置路径,确保网络正常运营,提高网络节点的可靠性。
考虑备选枢纽的选址模型是假定网络中的枢纽港有一定的失效概率,在枢纽港失效情景下,所有分配给该枢纽港的集装箱流将经过提前规划的备选枢纽转运,见图1。图1中网络中选定的枢纽港口为A、B和C,其备选枢纽港为D、F和I。在枢纽港正常运营情况下,按图1中的2号情景,以A、B和C为枢纽港,进行支线港集装箱的分配与运输;当枢纽港口发生失效事件,图1中枢纽港B关闭时,将变为图1中的3号情景,F港替代B港成为枢纽港,所有流经B枢纽港的集装箱自动分配给F港,最终满足节点间的运输需求。
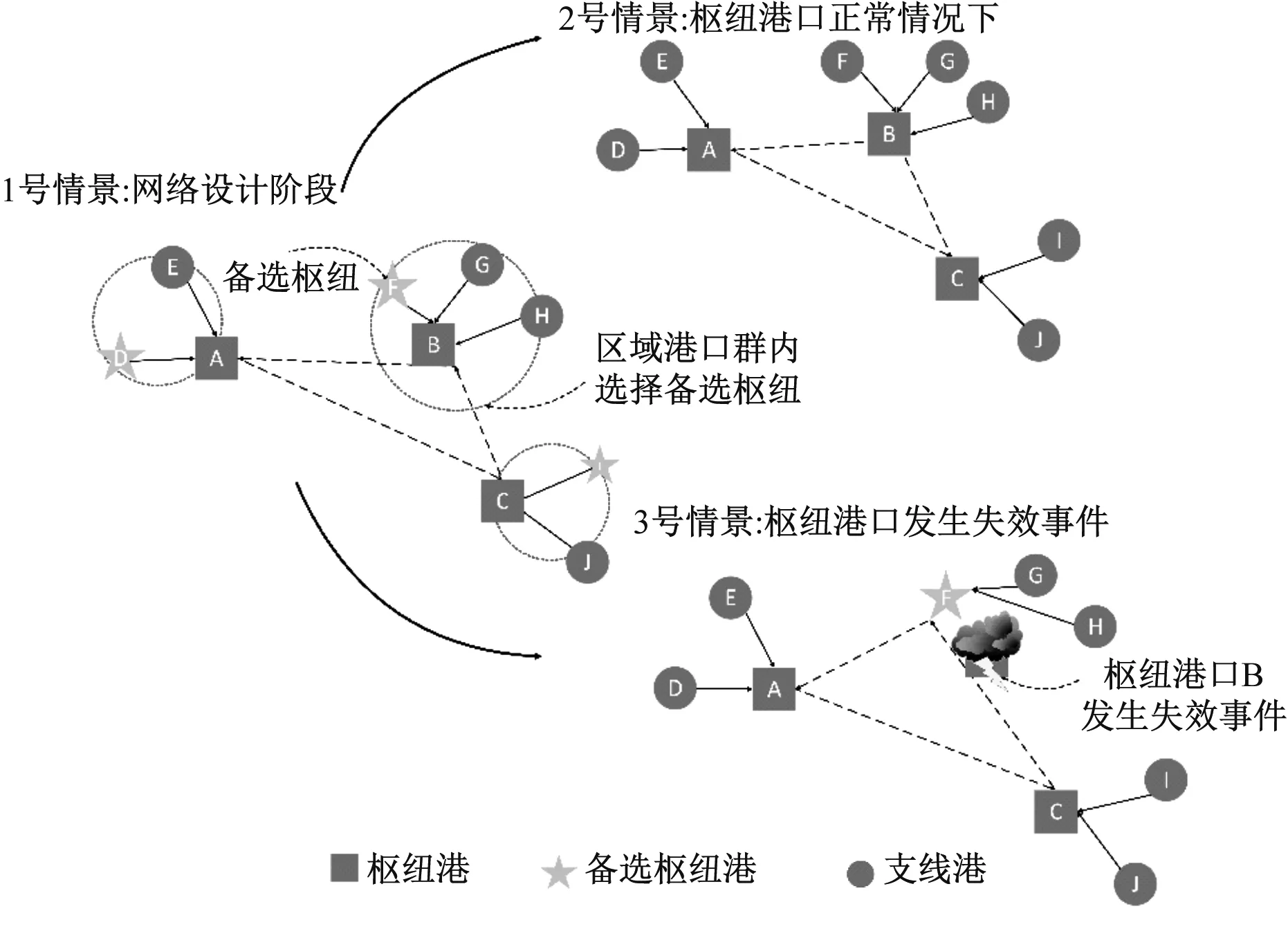
图1 可靠性轴辐式网络设计示意
由于枢纽港具有一定规模的经济效应,在实际操作中具有较大的集装箱运输量,因此在模型中考虑备选枢纽港口的通过能力。林天倚等[13]论证船舶延误随流量呈指数增长趋势,并利用ELHEDHLI等[14]提出的拥堵与流量的指数函数对其进行量化。本文考虑集装箱流通过备选枢纽港中转造成的额外成本,利用幂指数函数进行刻画,表示为
(1)
式(1)中:gn为在港口失效情况下,重置路径流经替代枢纽港口n的集装箱流。通过将该部分成本最小化,确保网络中重置路径分配集装箱流的合理性。
1.2 模型假设和符号说明
1)对本文研究的海运网络设计问题做出以下假设:
(1)研究对象为严格的单分配轴辐式网络,即1个支线港口只能分配到1个枢纽港口进行货物运输,支线港口之间不能连通;
(2)参考集装箱远洋运输航线,枢纽港之间的运输为1条跨区域的环绕式航线,船舶按次序挂靠枢纽港;
(3)所有港口相互独立,考虑失效事件发生的偶然性,每次仅允许1个港口失效;
(4)当港口失效时,流经备选枢纽港的额外流量假设为超过该港口在正常情况下的集装箱运输量,即超过该港口的最大通过能力;
(5)模型中不考虑重箱、空箱和租赁箱成本;
(6)模型适用于单个班轮公司,不考虑与其他公司联营、舱位互换和互租等情形。
2)决策变量
(2)
(3)
(4)
(5)
3)集合与参数
N为港口集合,P为枢纽港口集合,其中P⊆N;节点i,k,m,j∈N;W为起、讫港口对(i,j)的货流量,p为枢纽港数量;α为枢纽港口之间运输成本的折扣系数,0<α<1;cij为起、讫港口对(i,j)集装箱成本;Cikmj=Cik+αCkm+Cmj,为从起点港口i到枢纽港口k、从枢纽港口k到枢纽港口m、从枢纽港口m到目的港j的单位运输成本;THCk为集装箱在枢纽港k中转产生的单位中转成本;qk为枢纽港k发生港口失效事件的概率;qm为枢纽港m发生港口失效事件的概率;Qi为由i港发送的货流;Di为送至i港的货流。
1.3 模型构建
结合O’Kelly关于单分配轴辐式网络设计的模型,建立以成本最优为目标的轴辐式网络优化模型,相应的目标函数和约束条件如下。
1)目标函数为
(6)
(7)
(8)
(9)
(10)
Skm≤Hik,Skm≤Hjm;k,m≠k
(11)
(12)
(13)
Xikmj≤Skm,i,j≠i;k≠m
(14)
(15)
Xikmj∈{0,1},i,j∈N;k,m∈p;Hik∈{0,1},i∈N;k∈p
(16)
Skm∈{0,1},k,m∈p;Bikm∈{0,1},i,n∈N;
k∈p
(17)
2)模型以网络预期运输成本最小化为目标,式(6)为正常情况时和考虑港口失效情况时的期望运输成本,主要包括5部分,其中:第1部分为未受到干扰的网络的运输成本;第2部分为枢纽港口不能正常运营时,利用备选枢纽港口运输产生的重置路径成本;第3部分为当枢纽港口为启运港时,由于港口失效导致损失集装箱流所产生的惩罚成本;第4部分为备选枢纽港中转超过其港口通过能力的集装箱流产生的额外成本;第5部分为在枢纽港产生的转运费用。式(7)~式(10)为枢纽港选址的必备条件,其中:式(2)和式(3)为确保非枢纽港口通过枢纽港口进行集装箱中转;式(9)确保任意港口i只能配置到1个枢纽港进行集装箱运输;式(10)为公司拟决策的枢纽港口数量为p;式(10)~式(13)为确保枢纽港口间航线运输的有向性;式(11)为保证干线航线两端港口均为枢纽港口;式(12)为确保与枢纽港口相连的干线航线只有2条,且有向;式(13)为确保枢纽港口之间同向航线最多只有1条;式(14)为港口i到港口j的集装箱若经过枢纽港k和枢纽港m运输,则必经过枢纽边(k,m);式(15)为确保每个枢纽港口都有对应的备选枢纽港口,且备选枢纽港口为其支线港口;式(16)和式(17)为约束条件的非负性。
2 粒子群算法设计
目前,已有文献论证单分配枢纽选址模型为NP难问题[2],该模型由枢纽选址和配置2个问题组成,NP难问题为该模型的一个子问题。本文提出的模型即属于NP难问题。采用精确式算法求解消耗的时间较长,而粒子群算法具有易实现、精度高和收敛速度快等优点,可有效求解NP难问题。针对本文提出的枢纽选址问题,设计粒子群算法进行求解。算法的基本步骤如下:
1)设粒子数为M,在初始化范围内对粒子群进行随机初始化,包括初始化粒子位置P和速度v,分别为
P=(p1l,p2l,…,pml)
(18)
v=(v1l,v2l,…,vml)
(19)
对初始粒子进行编码,每个粒子pkl由1个2n的矩阵组成,代表1个选址方案,其中:n为港口数量;l为迭代次数。第1行从[0,n]范围内任取10个数字并进行排序,前p个元素表示该粒子中枢纽港的位置,p为网络中枢纽港个数;第2行确定支线港口的配置方式,在[1,p]范围内取随机数并取整,对应枢纽港的位置序号,即该支线港口对应的枢纽港口位置号码。本文从10个港口中选择3个枢纽港展示粒子编码方案初始化过程,代表该粒子群中某初始粒子的枢纽选址方案,见图2。

图2 初始化连续型粒子编码方案
2)根据选址问题需求,设计一定的方法将第1)步产生的连续性编码方案变为离散型编码方案,形成可行的枢纽选址方案。对第1行进行排序,前3位元素代表的序号即为该粒子选定的枢纽港口;对第2行元素进行取整,整数部分为对应港口配置的枢纽港口,根据该方式得到离散型粒子编码方案见图3。图3中:第1行枢纽港口为6、5和3,对应位置序号为1、2和3,第2行元素数字对应的位置序号即为其配置的枢纽港口。
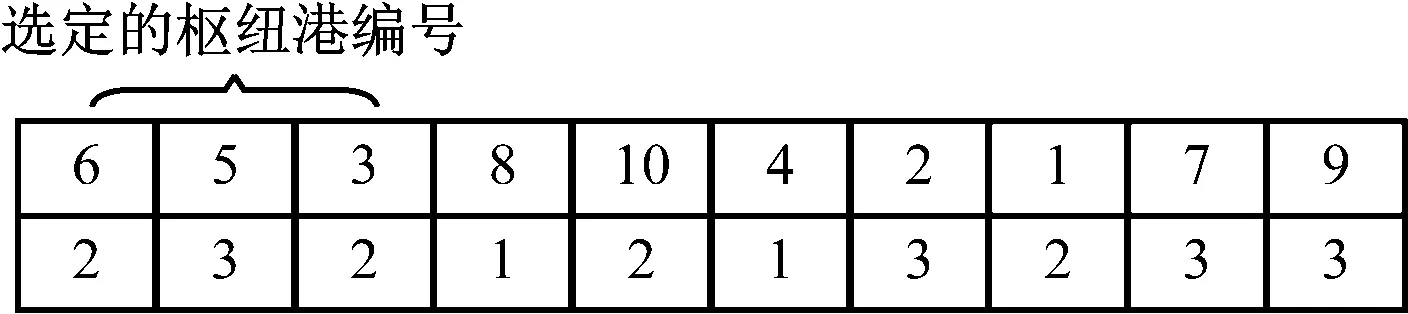
图3 初始化离散型粒子编码方案
3)为符合模型约束要求,确保支线港有且只有1个配置枢纽港,枢纽港配置的枢纽港为枢纽港本身,对第2行分配的枢纽港存在不匹配的方案进行修复。图3中:第1行表示选定6(1)、5(2)和3(3)等3个港口为枢纽港,括号中的数字代表在该方案中枢纽港口对应的位置序号。观察图3第2行第3位元素配置号码为2,对应的是5号枢纽港,即5号港口为3号港口的枢纽港口,这与3号港口应配置给3号枢纽港口约束不符。因此,需对该方案进行修正,修正说明见图4,修正后形成的轴辐式网络示意见图5。
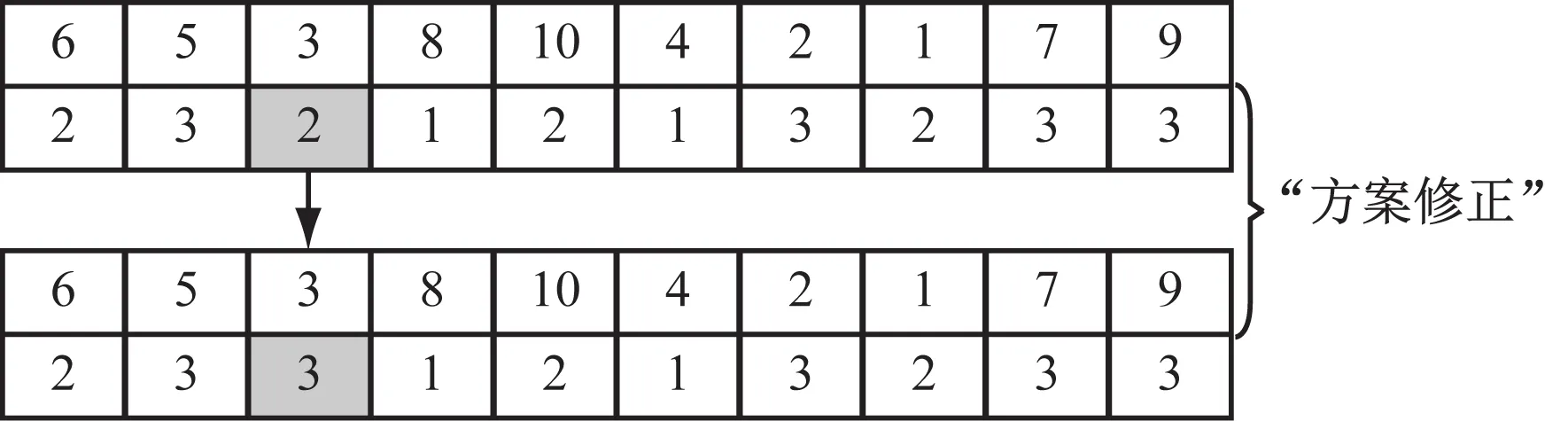
图4 初始化粒子方案修正说明
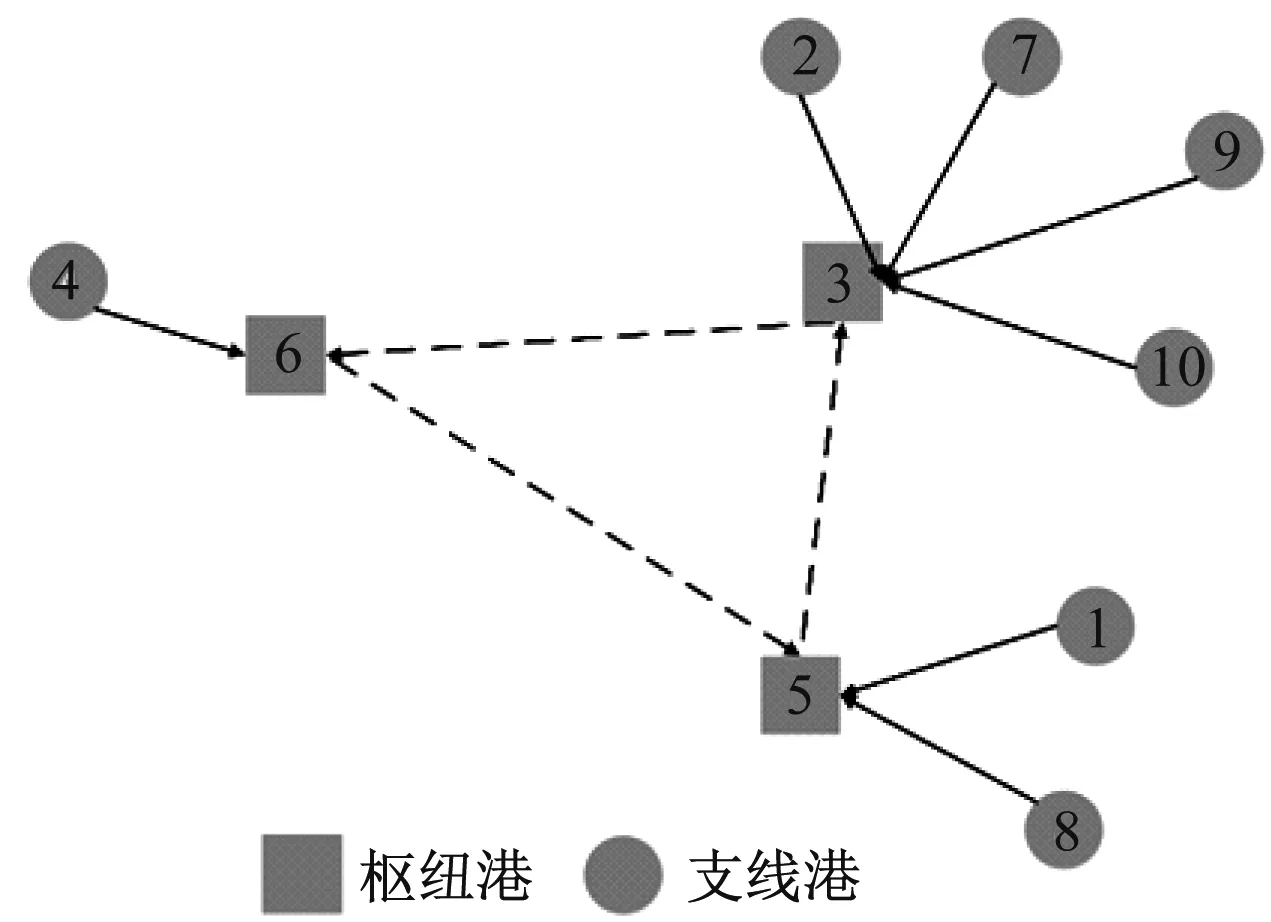
图5 粒子方案形成的网络示意
4)为每个枢纽港口选择备选枢纽港口,备选枢纽港口的选择方案是解决方案的一部分。对于港口来说,选择备选枢纽港的方法有3种:
(1)随机选择;
(2)验证所有可能的枢纽港方案;
(3)选择邻近的港口作为备选枢纽港口。
5)考虑到航运网络干线航线环状运输,备选枢纽将从第3)步中划分好的区域港口群中选择邻近的支线港作为备选枢纽港。
6)根据第4)步中粒子代表的枢纽选址方案,结合模型目标函数,计算各粒子的适应度值。假设目前每个粒子的适应度值即为该粒子当前最优解Pbestkl,整体粒子群中个体适应度值最优的为该粒子群的最优粒子,记为全局最优解Gbestl。根据式(19)和式(20)对当前粒子进行位置矢量和速度矢量更新,其中k为粒子群中第k个粒子,l为迭代次数。
(1)pk,l+1位置矢量更新公式为
pk,l+1=max[(pkl+vk,l+1),pmax]
(20)
式(20)中:pmax=p+1-ε,0<ε<1;l为迭代次数,最大迭代次数L。
(2)速度矢量更新公式为
vk,l+1=ωvkl+C1r1(Pbestkl-pkl)+C2r2(Gbestl-pkl),
k=1,2,…,n
(21)
式(21)中:C1和C2为学习因数;r1和r2为(0,1)范围内产生的随机数;ω为惯性系数。
7)对每个粒子的个体历史最优解与群体内的全局最优解相比较,若粒子个体最优解更好,则将其作为全局最优的位置,更新整个群体的全局最优解。
8)判断是否符合收敛条件,若符合,则停止迭代,输出最优解;否则,进行第5)步,继续迭代。
3 算例分析
本文以亚欧航线为例,选取该航线的10个港口,分别将其命名1~10号港,其中:1~6号港为亚洲港口;7~10号港为欧洲港口。对航线进行规划设计,从集合H中选出一定数量的枢纽港,确定其余港口与选定的枢纽港之间的分配关系。同时,确定枢纽港对应的备选枢纽港,形成航线网络。根据2018年各港口间贸易量和MULDER等[15]提到的数据港口间运输成本的计算,确定港口间的需求和运输成本,根据全球和平指数(Global Peace Index,GPI)设计港口完全失效概率,其中:1~10号港口对应的实际港口与完全失效概率见表1;各港口地理位置图见图6。
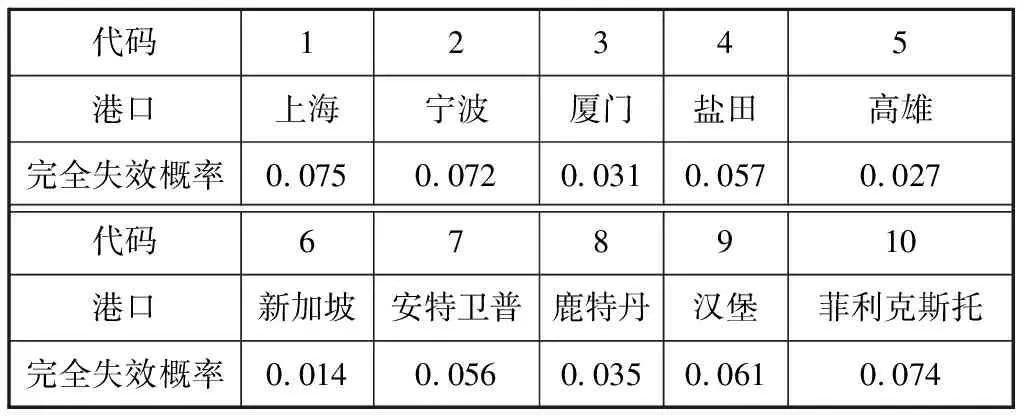
表1 各港口代码与对应的完全失效概率
在该航线的10个港口中,选择3个作为枢纽港,并为每个枢纽港选定备选枢纽港。对程序运行结果进行分析如下:
在10个港口中选择3个作为枢纽港口。远东地区港口有1(上海,枢纽港)、2(宁波)、3(厦门)、4(盐田,4号港作为1号港的备选枢纽港口)、6(新加披,枢纽港)和5(高雄,支线港,5号港为6号港备选枢纽港);欧洲地区港口有8(鹿特丹,枢纽港)、7(安特卫普,7号港作为6号港备选枢纽港口)、9(汉堡)和10(菲利克斯托,支线港)。
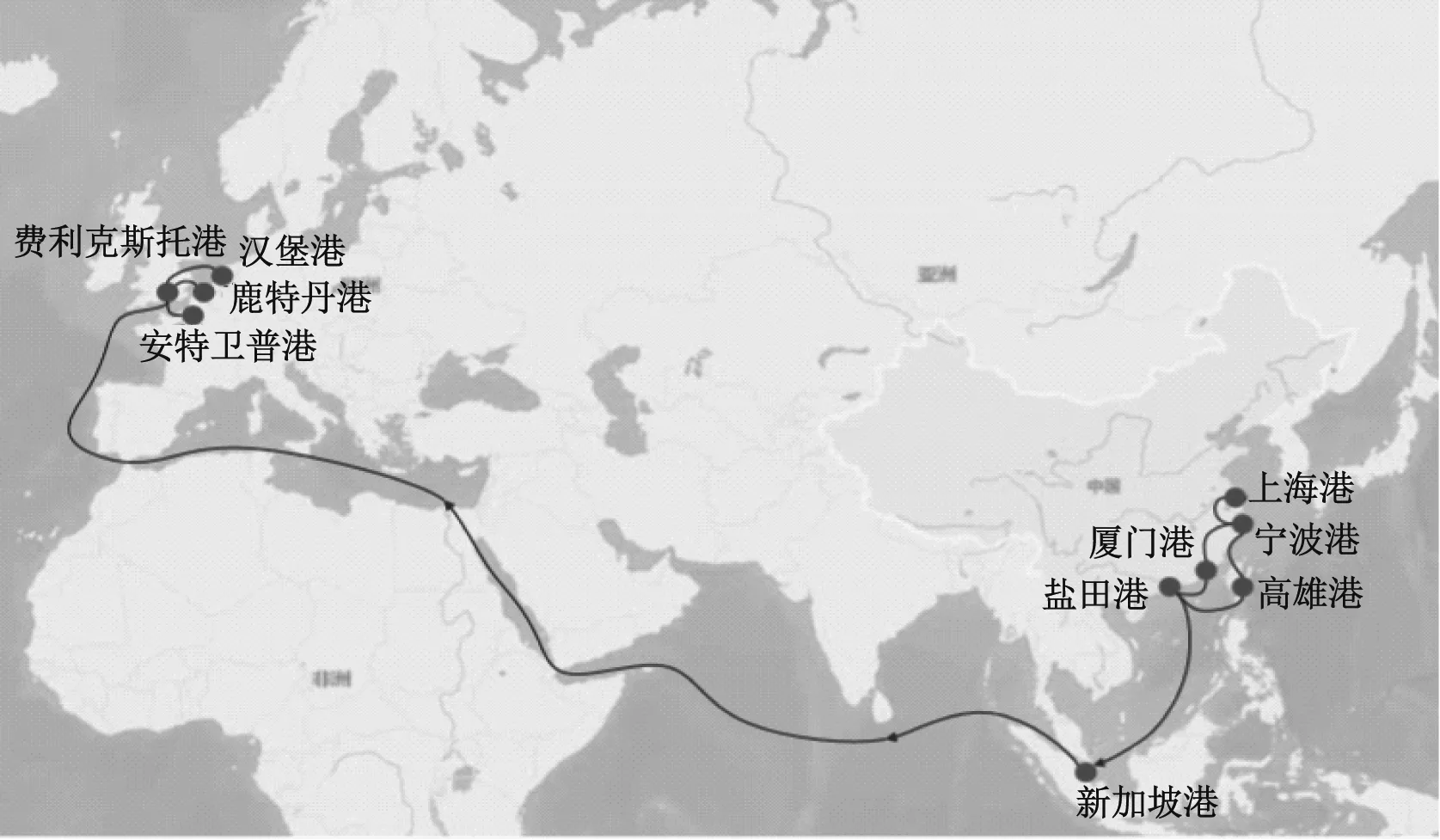
图6 算例各港口地理位置图
对比分析不同折扣系数下,考虑备选枢纽模型与不考虑备选枢纽模型的成本和网络中的流量,结果见表2。随着干线折扣系数的增大,轴辐式网络的干线经济效益下降,从而使得网络中的运输成本提高。由表2可知:考虑备选枢纽的模型运输量比不考虑备选枢纽的模型运输量高,尽管因绕行存在一定的成本,但避免了因枢纽港中转能力失效导致的集装箱流不能运输的现象,提高了网络的可靠性,最大程度降低了班轮公司的潜在损失。
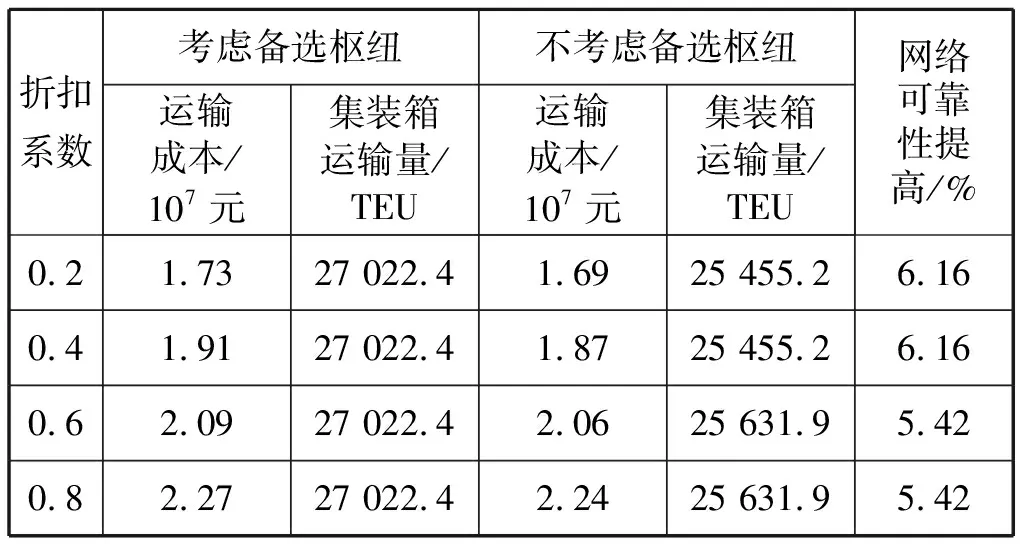
表2 传统模型与可靠性模型结果对比
4 结束语
本文研究集装箱班轮运输轴辐式网络设计中的枢纽港选址问题。从事前规划出发,考虑港口存在可能失效的风险,引入备选枢纽变量,以在正常情况下运输成本和受到失效事件影响重新规划路径产生的成本最小为目标,构建MINP模型。采用粒子群算法进行求解,验证模型的可行性。结果表明:随着折扣系数的变化,网络成本会发生变动,折扣系数越小,干线规模效应越明显,其运输成本越低。同时,对比分析考虑备选枢纽模型与不考虑枢纽模型的差异,结果表明,考虑备选枢纽模型求解运输的集装箱流大于不考虑备选枢纽模型,说明在网络设计阶段考虑备选枢纽可避免因港口失效而损失部分集装箱流,提高网络可靠性。由于港口间的需求、运输成本等数据难以获得,研究结果尚不能准确地反映实际情况,可探索在一些情境下轴辐式网络的设计趋势,扩宽对轴辐式网络不确定性的研究范围。同时,在全球班轮竞争日益激烈的背景下,为班轮公司的规划提供有效的策略,帮助班轮公司规避潜在网络风险,并提高客户满意度,从而提高班轮公司的品牌竞争力。

