考虑吸引力和可靠性的南海邮船航线优化模型

李伯棠, 袁炎清, 易 燕, 陈建平

(广州航海学院 港口与航运管理学院， 广州 510725)

纵观全球邮船旅游业近几十年的发展历程，邮船航线的区域性特征较为明显。当前，在“一带一路”、中国-东盟自贸区和粤港澳大湾区等建设的带动下，我国正积极与南海周边国家和地区开展邮船产业合作开发。在此背景下，为推进南海旅游资源得到更好的开发，需要寻找科学、高效和经济的邮船航线。

邮船航线设计的好坏体现在航线的吸引力上，即邮船停靠的港口及其腹地对游客的吸引程度。因此，除了考虑成本，还需选择有吸引力的港口，以提高所设计航线的吸引力。PAPATHANASSIS[1]认为当前有关具有吸引力的停靠港口选择问题的研究较少。LEONG等[2]对于邮船航线的设计，建立一个邮船航线中途港口选择的混合整数线性规划模型。HERSH等[3]在给定访问港口集合的情况下，建立船舶航行路径和调度的数学优化模型，并将其应用于从佛罗里达出发，可停靠牙买加、波多黎各和巴哈马等港口的邮船航线实际案例中；YANG等[4]将该模型应用到了我国沿海邮船航线规划上。然而，这些研究在建立邮船航线模型时并没有考虑航线的吸引力。

邮船航线的设计还要考虑其他影响因素，航速就是其中一个重要因素。[5]控制航速可降低油耗，在不需要保持最大速度航行的情况下，降低航速可显著降低成本。[6]将速度作为决策变量的方案已在海上运输中得到广泛应用，而速度的选择对经济成本和环境保护均有影响[7-8]，例如：NORSTAD等[9]和WEN等[10]研究了在船舶航速可变的情况下，不定期船的航线和调度优化；镇璐等[11]分析了排放控制区对船舶航速决策的影响。在一些以减少污染为目标的绿色物流应用中，也考虑速度优化，例如：BEKTAS等[12]提出了污染路径问题；FRANCESCHETTI等[13]提出在文献[12]基础上考虑时间问题。在航线设计中对航速的决策尽管已成为近年来海上货运领域的一个热门话题，但在旅客运输中很少考虑。

港口中断情况也会影响航线的吸引力和总成本。尽管邮船或航运企业可确保其设计的航线正常开展业务，但航线的运营仍有因受外界不确定因素(如政策改变、恶劣气候、旅游淡季、战争、传染性疾病和政治动乱等)的影响而中断在某港口停靠的风险，因此需将航线的可靠性考虑在航线规划的范围内。BROUER等[14]揭示了班轮运输中断对成本和货物按时交付的影响，提出采用船舶调度恢复模型评估给定的中断场景，并以马士基公司为例证明了该模型在节约成本方面的有效性；FISCHER等[15]针对滚装班轮运输中船队的中断问题，以成本最小为目标，建立一个稳健的船队分配给预定航程的数学模型，案例结果表明，采用该模型能提高鲁棒性，降低计划的实际成本，缩短航程的总延误时间；SUN等[16]考虑班轮运输的不确定性对全球供应链可靠性的影响，提出一种新的风险规避模型，建立给定可靠性水平下装运作业分配风险成本的封闭形式，验证装运不确定性对生产调度和作业成本的影响；ACHURRA-GONZALEZ等[17]应用较少依赖复杂资料的技术，建立一种集装箱分配模型，并以东南亚—欧洲班轮运输贸易为例，证明港口中断情景的后半部分区域内连接的脆弱性更高；LI等[18]在战术层面班轮运输网络设计中考虑中断和加速，构建一个可靠的非线性规划模型，利用算例验证模型的有效性并提出相应的建议。然而,上述研究只针对中断情况下货物的可靠航线运输网络，没有对旅客运输的可靠航线设计进行研究。

综上所述，本文针对邮船航线提出以下问题：

1)如何确定南海区域内邮船航线挂靠港口的吸引力。

2)在整合环南海各种邮船发展资源时，联合“新海上丝绸之路”沿线国家和地区的邮船港口、沿海城市、旅行社、邮船公司共同参与，如何建立南海沿线邮船旅游发展规划航线设计。

3)面对中断风险时，邮船航线如何保持可靠性。

针对上述问题，本文在考虑邮船航线设计可靠性的基础下，对停靠港口选定及其排序、每航段航速的设定和船舶在港时间(开始时间和服务时间)进行决策，以总成本最小化和航线吸引力最大化为目标，建立邮船航线混合线性规划模型，并将非起点港和目的港为导向的数学模型应用到南海邮船航线开发的实际问题中。

1 问题描述

本文考虑在一个完整邮船航程计划内，南海地区邮船航线的设计，包括停靠港口的选定和排序、每航段航速的设定和船舶在港时间(开始时间和服务时间)决策。南海地区可停靠的港口有广州、深圳、珠海、海口、北海、三亚、厦门、新加坡、香港、马来西亚、菲律宾、马来西亚、文莱、印尼、新加坡、泰国、柬埔寨和越南等国家或地区的邮船港口，在以上港口中选择适合的港口并按一定顺序排列组成航线，可由1条或多条线路组成，不同航线可停靠同一港口。每条航线选择1种船型，船舶可采用不同航速航行。为避免不同邮船在同一天访问同一个港口，以小时为时间单位，1周内每天都可在特定的时间窗内访问港口，时间窗规定邮船允许的到达时间和离开时间。MANCINI等[19]在确定的起点港和目的港建立航线网络优化模型，然而受外界因素的影响，起点港和目的港不适宜停靠。为保证航线的多样性，本文设定多个可选起点港和目的港，并在考虑港口中断的情况下，以最小化总成本和最大化航线吸引力为目标，建立邮船航线优化模型。

随着人们生活水平的提高和带薪假期政策的落实，新的旅游方式的需求增多，邮船旅游市场的发展潜力变大，调查邮船挂靠港口的岸上旅游项目是否具有吸引力显得十分重要。一般来说，港口吸引力是港口各类条件和若干因素综合作用下形成的对旅游者的诱惑程度，该诱惑程度是个人在主观上对港口的模糊认识。因此，与以往采用指标确定港口的吸引力不同，本文认为港口吸引力是个人在主观上口头模糊评价的综合吸引力。

通过问卷调查的形式了解消费者对南海邮船旅游的港口及其所在城市的主观评价，调查对象主要是有意愿的游客。调查问卷内容分2部分：

1)受访者的个人基本信息，包括性别、年龄、受教育程度、职业、收入等。

2)受访者根据口头评价的分类中的7个选项(见表1)，对每个港口选择1项进行口头评价。

表1 口头评价的分类

在受访者给出评价之后，利用群体决策环境下的口头评价方法[20]确定各港口的吸引力。口头评价分为7类(如表1所示)，口头评价的隶属函数见图1，其中μL(α)为每个口头评价的隶属度函数，μL(α)∈[0,1]。本文以3个受访者和3个港口为例, 给出港口吸引力计算的3个步骤。

图1 口头评价的隶属函数

1)确定受访者的权重。采用程度模糊层次分析法[19]确定各受访者的权重。由邮船企业销售部主管根据受访者的个人基本信息对各受访者之间重要性的比较作口头评价，其中相同成员的比较用M表示[21]，具体见表2(假设存在3个受访者)。

表2 受访者的比较

通过采用程度模糊层次分析法进行计算，得到受访者权重为

W′=(0.211, 0.665, 1)

(1)

归一化后变为

W=(0.11, 0.36, 0.53)

(2)

表3 受访者对港口的吸引力评价

第k个受访者对第i个港口的期望吸引力的计算式为

(3)

式(3)中:乐观指标α∈[0,1]。

(1)当α=0时，表示悲观的受访者，得总积分值为

(4)

(2)当α=0.5时，表示折中的受访者，得总积分值为

(5)

(3)当α=1时，表示乐观的受访者，得总积分值为

(6)

3)港口的整体吸引力。计算各港口的整体吸引力为

(7)

根据前2个步骤中的数据得到港口的整体吸引力见表4。

表4 港口的整体吸引力

2 建立模型

2.1 符号说明

2.1.1集合

I为可用备选港口集合,i,j∈I；D为邮船出发港的集合,D⊆I；A为邮船到达港的集合,A⊆I,D∩A=∅;K为邮船船型集合,k∈K；R为时间间隔(天数)集合,r∈R；S为设施的能力水平集合,s∈S；P为情景集合,p∈P。

2.1.2参数

2.1.3决策变量

2.2 目标函数和约束条件

1)目标函数1：最小化总成本，总成本包括航线的航行成本、前后期服务成本、在港固定成本和在港服务成本。

(8)

2)目标函数2：最大化每条航线的吸引力。

(9)

根据模型假设条件，目标函数的决策变量需满足的约束条件为

(10)

xksij=0,k∈K;s∈S;i,j∈D

(11)

xksij=0,k∈K;s∈S;i,j∈A

(12)

(13)

i∈I{D,A},k∈K;i≠j

(14)

(15)

(16)

(17)

(18)

(19)

(20)

p∈P;i∈I{D,A};r∈R;k∈K

(21)

p∈P;i=I{D,A};k∈K;r∈R

(22)

p∈P;i∈A;r∈R;k∈K

(23)

(24)

stki](1-τpi),p∈P;i,j∈I;k∈K

(25)

p∈P;i∈I

(26)

(27)

(28)

2×hkk′i≤uki+uk′i,i∈I;k∈K;k′∈K

(29)

hkk′i+1≥uki+uk′i,i∈I;k∈K;k′∈K

(30)

(31)

xksij,ykri,uki,hkk′i∈{0,1},

i,j∈I;k,k′∈K;s∈S;r∈R

(32)

(33)

式(8)～式(33)中:式(10)限制除了情况0以外，各情况目标函数1的值不大于一定比例下各情况目标函数的最优值；式(11)限制邮船不能从一个起点港到另一个起点港；式(12)限制邮船不能从一个终点港到另一个终点港；式(13)限制邮船从规定的起点出发；式(14)表示邮船出发后按顺序经过中间停靠点；式(15)表示邮船在某一终点港停靠，结束整个航程；式(16)表示邮船在从其他港口去往某一港口时，只能用1种航速进行航行；式(17)确定船舶停靠的起点港和中间港；式(18)确定船舶停靠的终点港；式(19)限制中间停靠港口每天只能停靠1艘船；式(20)限制在某情景某邮船在某天停靠在某一港口的服务时间不低于所停港口的最短服务时间；式(21)限制在某一情景下某艘邮船在某中间港口的开始服务时间不得早于当天的14:00；式(22)限制在某一情景下某艘邮船在某中间港的开始服务时间、服务时间和在港所需服务时间之和不得晚于当天16:00；式(23)限制在某一情景下某艘邮船在某终点港口的开始服务时间不得早于当天的12:00；式(24)限制在某一情景下前一个港口开始服务时间、船在港所需服务时间、离港时间、前后两港航行时间和后一港口的进港时间之和不得早于紧接港口的开始服务时间；式(25)限制在某一情景下紧接港口的开始服务时间与前后两港航行时间之和不得早于前一个港口开始服务时间、港口所需的服务时间和船舶在港所需服务时间之和；式(26)限定每种情形下对于每个港口的最少和最多航线数量；式(27)限制每艘船停靠港口的下限；式(28)限制2条航线共同停靠港口的数量不能超过限定值；式(29)和式(30)限制hkk′i在2艘邮船停靠同一港口时才能为1，否则强制为0；式(31)限制选定确定船舶停靠的港口的逻辑关系；式(32)限定变量只能取0和1；式(33)限定变量不小于0。

(34)

3 解决方法

第2节所建模型是一个多目标混合整数非线性规划模型，其中非线性部分在于目标函数2。采用ε-约束方法使模型线性化并得到Pareto解，以最重要的目标为主要目标，以其他目标为约束。[23]总成本被视为主要目标，由吸引力最大化的目标函数2被改为新的约束条件，得到可直接求解的单目标混合整数线性规划模型为

(35)

通过改变约束目标函数2的右侧εk(目标2限制的最小值)，可得到问题的有效解。获得所有的解决方案之后，决策者可根据其结果做出决策。[24-25]

综合上述分析，给出求解第2节所建模型的算法步骤见图2。

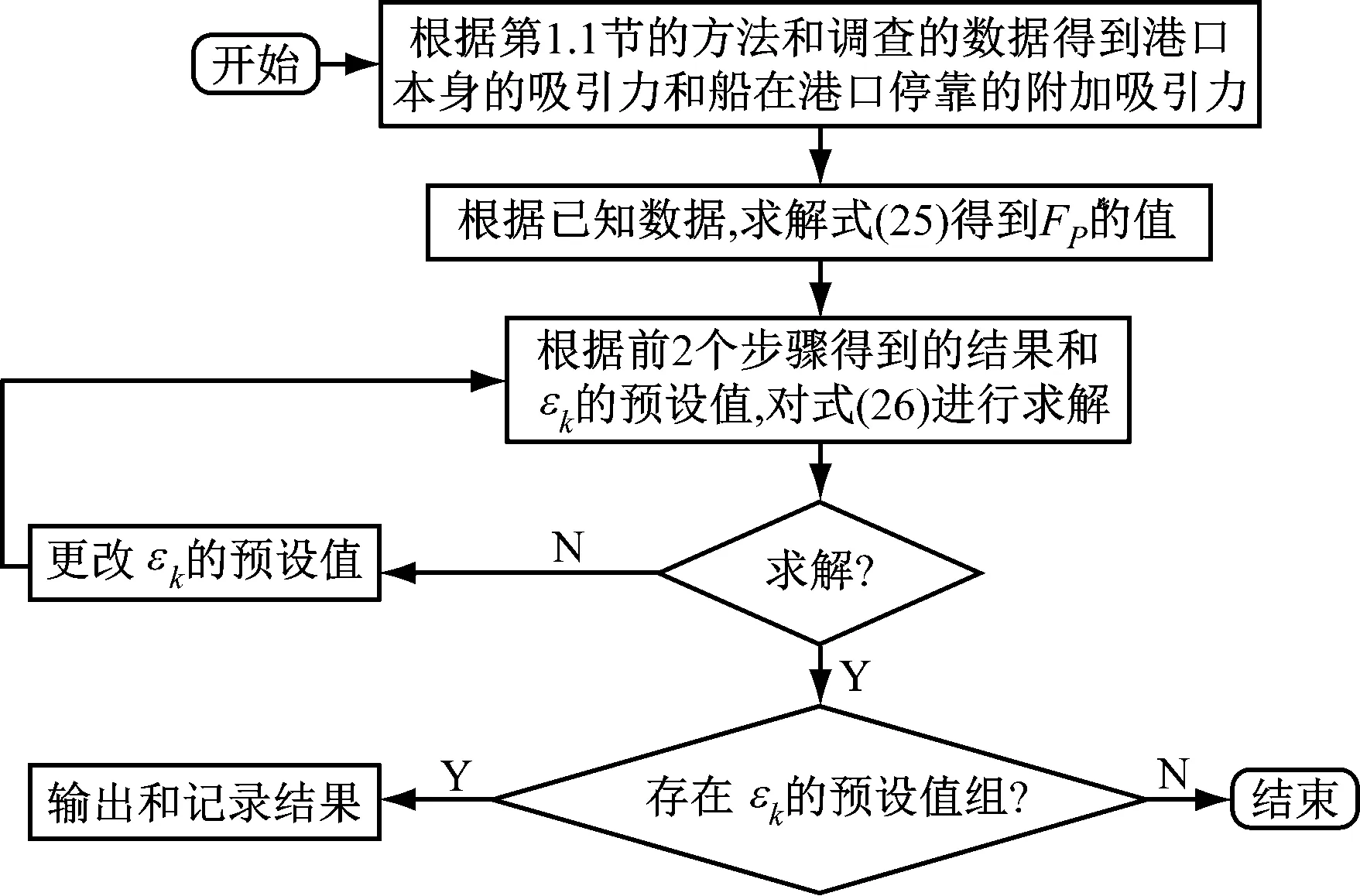
图2 模型求解算法

4 案例分析

根据以上数据，本文选择中国境内的8个港口作为出发港，选择马来西亚境内的13个港口作为到达港。模型采用CPLEX12.8软件进行编程求解。最后，通过改变部分参数值得到模型结果有关数据(见表5～表8)。

表5 模型结果有关数据(Qmin=0,Qmax=1,θ=5,φ=5)

表6 模型结果有关数据(Qmin=0,Qmax=2,θ=5,φ=5)

表7 模型结果有关数据(Qmin=0,Qmax=3,θ=5,φ=5)

表8 模型结果有关数据(Qmin=0,Qmax=3,θ=6,φ=6)

成本变化曲线见图3。由表5～表9和图3可知：随着要求目标函数2中每条航线最低吸引力的增大，总成本和吸引力都在增加，违反表1～表3的程度也有一定程度的增加，说明总成本与吸引力之间存在一定程度的正相关关系。对于可靠性来说，随着吸引力的增加，违反程度也在增加，说明在一部分港口有可能中断的情况下，为增加吸引力，不得不违反某种情况的最优情况，停靠在一些较远且吸引力较大的港口，但会增加成本，导致违反程度变大。通过对比表7和表8可知:在改变航线的最少停靠港口数时，由于停靠的港口变多，使得航线不得不选择增加必要的费用，同时选择了某些吸引力较低的港口，因此航线整体的吸引力有所下降。

吸引力变化曲线见图4～图7。由图4～图7可知:随着要求目标2每条航线的最低吸引力的增加，吸引力的变化呈现一种类似线性化的增长模式。成本变化对比曲线见图8。由图8可知：港口数量的增加会导致成本增加，且增加幅度不同导致呈现一种非线性的增加，这是因为要保证航线的吸引力和可靠性，需付出更多的成本代价，而成本增加的幅度在不同港口中断情况下各有不同。

图3 成本变化曲线

图4 吸引力变化曲线(Qmin=0,Qmax=1,θ=5,φ=5))

图5 吸引力变化曲线(Qmin=0,Qmax=2,θ=5,φ=5))

图6 吸引力变化曲线(Qmin=0,Qmax=3,θ=5,φ=5))

图7 吸引力变化曲线(Qmin=0,Qmax=4,θ=6,φ=6))

图8 成本变化对比曲线

在所得数据结果中，广州港、深圳港、厦门港、香港港、新加坡港、长滩岛港、斯里巴加湾港、马尼拉、胡志明市、曼谷、芽庄、槟城、普吉岛、马六甲和巴生港等邮船港口被选择作为航线停靠次数最多的港口，说明这些港口在港口设施、安全、交通便利性、城市建设和旅游资源等方面都处于较高的水平。本文给出表5中的ε=0.8的最优航线及各航段航速(见表9和图9)。

表9 最优航速 n mile/h

图9 最优航线网络图

根据表5～表8，可得到图3～图8。由上述分析可知，邮船企业管理人员应多方考虑,保持吸引力与总成本的平衡。同时，还应考虑由于外界或港口自身因素导致港口中断而降低已制制航线的可靠性，综合决策出适合南海邮船航线共同开发的航线网络。

5 结束语

本文以南海邮船航线网络为研究对象，考虑港口中断的情况，以总成本最小化和航线吸引力最大化为目标，建立无限制起止港口的双目标邮船航线混合线性规划模型，并给出求解算法，同时通过案例证明模型的适用性，验证结果可为企业提供决策支持和方法指导。

后续研究将着重全面考虑南海邮船航线的船舶环境污染问题，从可持续和绿色发展等方面对邮船航线进行重新规划。此外，在实际情况中，当问题规模扩大或出现某些特殊数据时，会使模型求解的难度增加，需寻找更高效的算法对模型进行求解，以扩大模型的应用范围。