PIDAS工艺评估和工艺设计模型开发
陈欢欢,刘 晔,闫 博
(宝山钢铁股份有限公司中央研究院,上海 201999)
轧制过程材料组织性能预测是利用物理冶金学、机器学习、计算机视觉等模型,对轧制过程中的各种金属学现象进行计算机模拟,预测出轧后产品组织状态和力学性能,进行成分和轧制工艺的优化设计,从而实现对产品的质量控制[1]。随着生产数据库的不断积累和算法的不断进步,机器学习方法正在被重点关注,开始被大量地应用于组织性能预测。
本文首先开发了一种工艺评估模型,它能够根据用户设置的化学成分、产品规格、工艺参数和所需要的预测精度,评估产品性能值所在的区间。此模型的基础是自主开发的概率区间估计算法,它通过全面对比不同机器学习回归模型的效果,和充分考虑历史生产数据的分布规律,预测性能值可能落在的区间,以及落在此区间的可能性。本文以此算法为基础,以一种微合金高强钢为例,开发了PIDAS工艺评估模型。
同时又开发了一种工艺设计模型,它能够根据用户设置的化学成分、产品规格以及带有权重的性能目标,设计最优的轧制冷却参数。此模型的基础是本文中提出的自定义权重的模拟退火算法,它是一种基于蒙特卡洛思想设计的近似求解最优化问题的方法。在此算法基础上,借助于工艺评估模型,又开发了PIDAS工艺设计模型。
1 工艺评估模型
本章以一种微合金高强钢为例,介绍所开发PIDAS工艺评估模型。PIDAS系统已经收集了近两年该钢种生产过程的大量数据,其中包含了产品规格、化学成分、工艺参数和组织性能等。根据该钢种用途和特点,反映其好坏的基本性能有5项:抗拉强度、屈服强度、屈强比、断裂延伸率和剪切面积分数。通过对该钢种大生产过程进行深入的冶金学原理分析和大生产数据的分析,确定了影响产品性能的20项主要因素:
(1) 产品规格(3项):中间坯厚度、目标厚度、目标宽度。
(2) 化学成分(11项):C、Mn、Si、Nb、Ti、V、Cu、B、Cr、Ni、Mo。
(3) 温度参数(6项):出炉温度、开轧温度、终轧温度、冷速、开冷温度、终冷温度。
工艺评估模型能够根据上述20项工艺参数,精准预测5项性能所在的区间,以及真实值位于此区间内的概率。
1.1 概率区间估计算法
机器学习算法的本质是在特征和目标之间找到合适的映射关系[2],分为分类算法和回归算法两种[3],其中常见的回归算法有线性回归(Linear Regression)、 K近邻回归(KNN Regressor)、支持向量回归(SVR)、岭回归(Ridge)、Lasso回归、多层感知器回归(MLPRegressor)、决策树回归(DecisionTree)、极限树回归(ExtraTree)、极限梯度提升回归(XGBoost)、随机森林回归(RandomForest)、AdaBoost、梯度提升树回归(Gradient Boost)、引导聚集回归(Bagging),用REG_Model表示这些回归算法组成的集合。基于机器学习的材料性能预测流程如图1所示。

图1 回归方法流程图
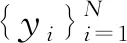
(1)
然而,中厚板组织性能的预测受检测手段、数据通讯、组织性能不均匀等诸多因素的影响[1],使得机器学习预测模型的精度并不是特别高;同时,由于生产过程的多工序性,使得在建立模型的时候不可能把所有特征都考虑在内,这样就导致了虽然模型对于相同的特征预测得到了相同的性能,但与实际性能间还可能会有一定差距,因为并没有考虑其他特征的影响。于是将机器学习方法应用到中厚板的组织性能预测上时,需要做一定改进。
不同于传统机器学习算法预测得到一个确定的值,区间估计算法预测得到的是一个区间值,以及真实值落在这个区间的概率,即准确性。文献[4-8]中分别提出了bootstrap,Bayesian,mean-variance estimation,delta 和 neural network的方法,然而这五种方法并没有尝试在不同准确率下的区间估计,也即调整准确率得到不同的区间估计。在这里本文提出了概率区间估计算法,解决了上述问题,其流程图如图2所示。
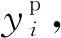

图2 概率区间估计算法流程图
(2)
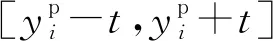
这样最终构建的模型一方面综合对比了常见机器学习回归模型的准确度,并选出最优的,另一方面又充分利用了历史数据的分布规律,用区间预测代替常见的单值预测,这样便能消除原始数据因为受检测手段、数据通讯、组织性能不均匀导致的不精确性以及生产的多工序性带来的影响。同时通过不同的acc下对应不同t值,实现了不同准确率下的区间估计,这满足了工艺设计人员对于不同精度下估计的需求。算法的伪代码如下:
算法1 概率区间估计算法
输入:历史生产数据data,REG_Model,Accuracy.
输出:最佳回归模型,不同准确率下的区间阈值.
1.threshold=Ø
2.for model in REG_Model do
3. train model on data;
4.end for
5.choose the best modelMas the candidate model.
7.for acc in Accuracy do
8. adjust and findtsuch that
9. threshold=threshold∪{t};
10.end for
11.returnM,threshold.
1.2 DWTT工艺评估模型
DWTT是用来检测材料韧性的试验,在这里特指DWTT剪切面积分数,其值在0~100之间,DWTT是否大于85(或95)是衡量抗脆性开裂能力的一个重要指标。文中将DWTT评估模型分成了两个小的模型:分类模型和回归模型。通过AdaBoost构建的分类模型能根据20个工艺参数预测产品DWTT值是否大于85。对于值在85以上的DWTT,本文根据前文提出的概率区间估计算法,构建了回归模型。流程图如图3所示。
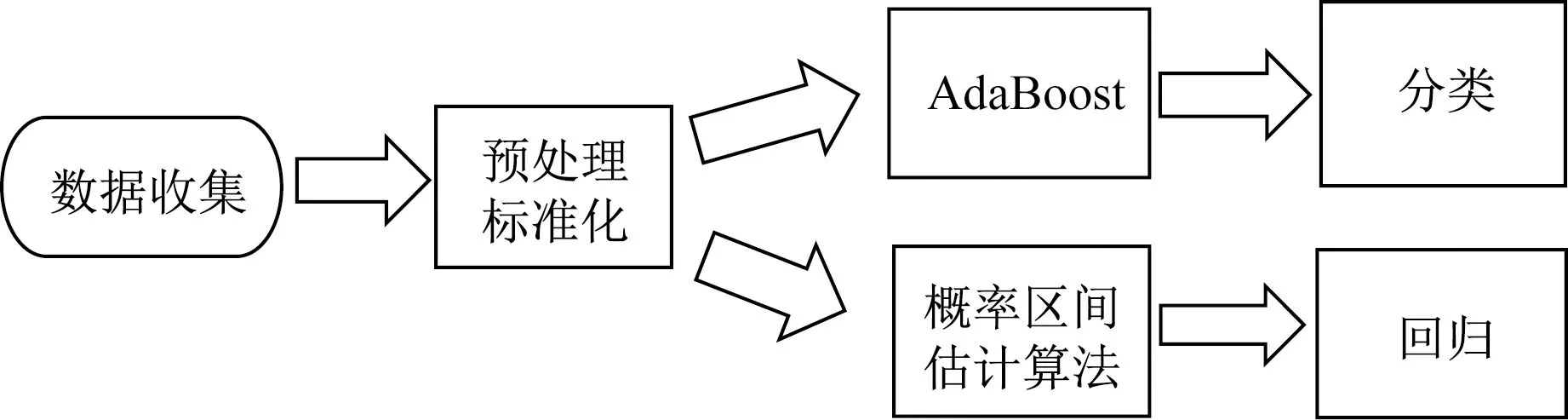
图3 DWTT工艺评估模型流程图
从PIDAS数据库中导出近两年对象钢种生产数据,同时只保留-10 ℃试验环境下DWTT的测量数据,删去空值所在的行后还剩下21 853条数据,随机地将数据集分成两部分,其中80%用作训练集,20%用作测试集。为了消除工艺参数数量级差别造成的影响,对工艺参数做了标准化的处理;在构建分类模型时,将85以上的DWTT赋为1,总共有21 087条,85以下的赋为0,总共有766条。
1.2.1 DWTT分类模型构建
文中采用AdaBoost算法构建DWTT的分类模型。AdaBoost算法是基于Boosting思想的机器学习算法,其核心思想是针对同一个训练集训练得到不同的决策树弱分类器,然后把这些弱分类器集合起来,构成一个强分类器[9],其中影响模型好坏的重要参数是弱分类器的个数(n_estimators)。
分类模型的评价标准除了准确率以外,还有精确率、召回率等,混淆矩阵如表1所示,Positive代表DWTT值超过85,Negative代表DWTT值低于85。

表1 混淆矩阵
准确率Accuracy为分类模型所有判断正确结果占总观测值的比重:
(3)
精确率Precision是模型预测为Positive的结果中模型预测正确的比重:
(4)
仅用准确率来衡量分类模型是不准确的,尤其对于负样本量比较少的数据,因为可以构建这样一个模型:预测全部结果都为Positive,这依然能达到很高的Accuracy,但这显然是不合理的。于是对于DWTT分类,除了评估模型的Accuracy,同时评估了模型Precision,即模型预测DWTT超过85时DWTT真实值超过85的概率。
在具体模型构建的过程中,本文采用AdaBoost算法训练了弱分类器个数从1~400的分类模型,各个模型在训练集和测试集上的Accuracy,以及Precision如图4所示。
从训练结果可以看到,分类器的个数在270时,模型在训练集、测试集上的准确率以及精确率同时达到了最优,分别为0.960 4、0.971 0和0.972 7,取得了比较精准的预测。
1.2.2 DWTT概率区间模型构建
上一节建立DWTT的分类模型,它可以根据工艺参数精准地预测DWTT是否大于85。如果大于85,工艺设计人员仍关心其值可能落在的区间,这节用第一章提出的概率区间估计算法构建区DWTT概率区间估计模型,它能评估DWTT在不同精度下可能落在的区间。我们逐步地在DWTT数据上实施算法1。

图4 AdaBoost 模型训练
首先是比较常见的回归模型在DWTT数据集上的表现,并用模型在训练集和测试集上的r2来找出最优模型,其结果如表2所示。

表2 常见机器学习回归算法在DWTT数据集上的训练结果
由表2可以验证前文中提到的,没有模型能够达到同时在训练集和测试集上达到比较高的准确率。并且可以看出,DecisionTree和ExtraTree 出现了过拟合现象。综合比较,本文选用Bagging作为下步区间估计的最优模型。
接下来对Bagging回归做进一步参数优化。BaggingRegressor是一种有放回的抽样训练的方法,每次从总样本集中随机地有放回抽取部分小样本,用决策树训练便得到一个回归模型,最后用取平均的方法得到最终的预测值,同上节AdaBoost一样,影响Bagging模型好坏的重要参数是弱分类器的个数(estimators)。我们采用BaggingRegressor算法训练了弱分类器个数从1~300的分类模型,各个模型在训练集和测试集上的Accuracy如图5。
于是选取弱分类器的个数为50,此时模型已经在训练集和测试集上达到了比较高的准确率。
接下来根据算法1的7~10步计算不同精度下的阈值,结果如表3所示。
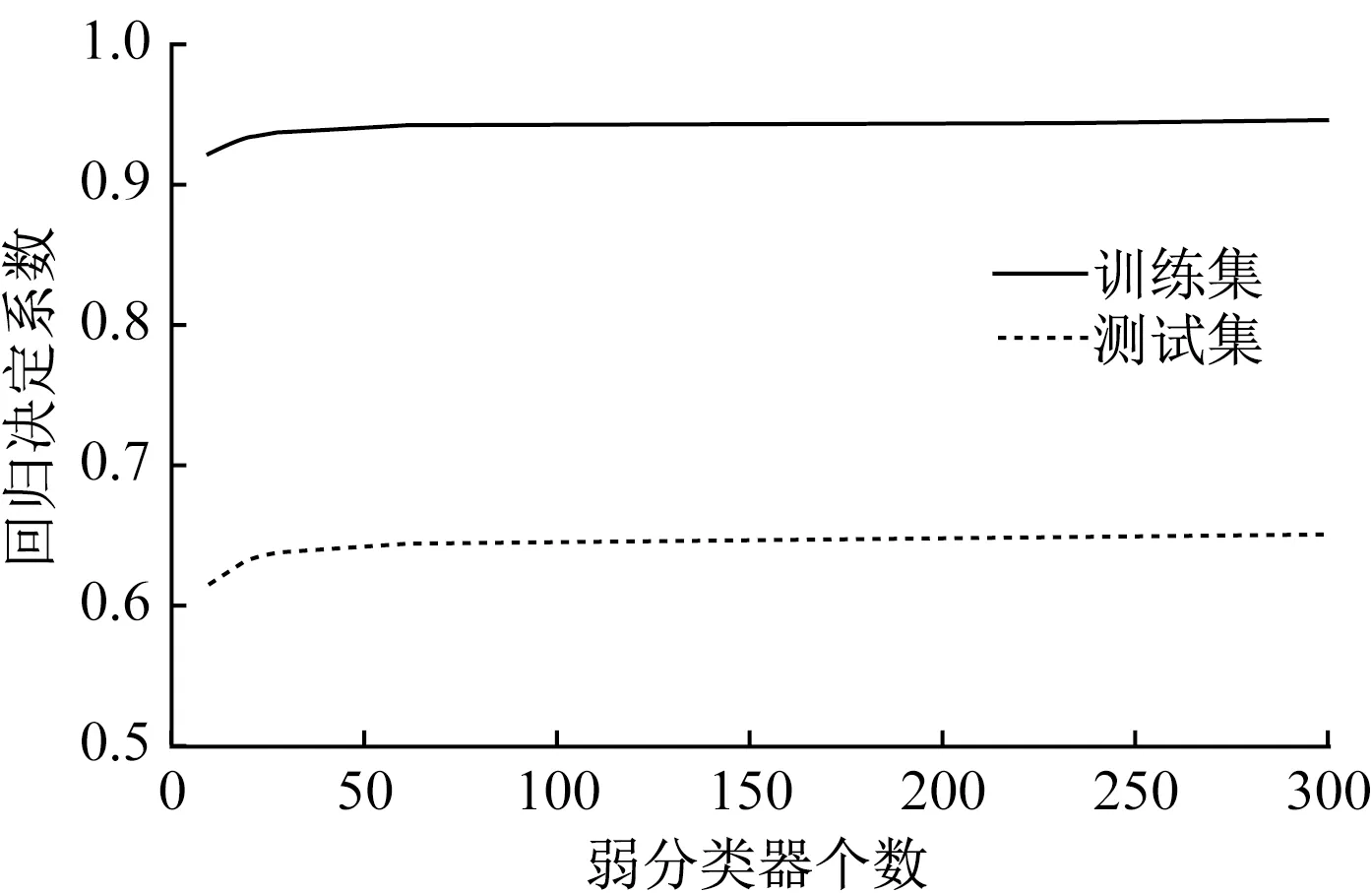
图5 BaggingRegressor模型训练

表3 不同准确率下的阈值
我们以准确率为90%时模型的预测结果来展示模型表示的含义。
图6中任意选取了30个DWTT真实值和其对应的模型预测值,其中黑色实线代表真实值,蓝色线段组成的区间代表模型在该点的预测值,线段长最多为2·Threshold=5.6。从中可以看到,真实值绝大多数落在了预测的蓝色区间中,90%的含义是历史数据以不低于90%的概率落在预测的区间中。

图6 准确率为90%时DWTT真实值和模型预测的区间值
同样地,当准确率为80%时,模型预测的结果和真实值如图7所示。
预测的区间长度为2·Threshold=3.6,和准确率为90%时相比,真实值不落在预测区间中的点的个数增加了,它损失了一定的准确度,但提升了一定的精度。同样的解释对于其他准确度,区间范围越小,准确率越低。
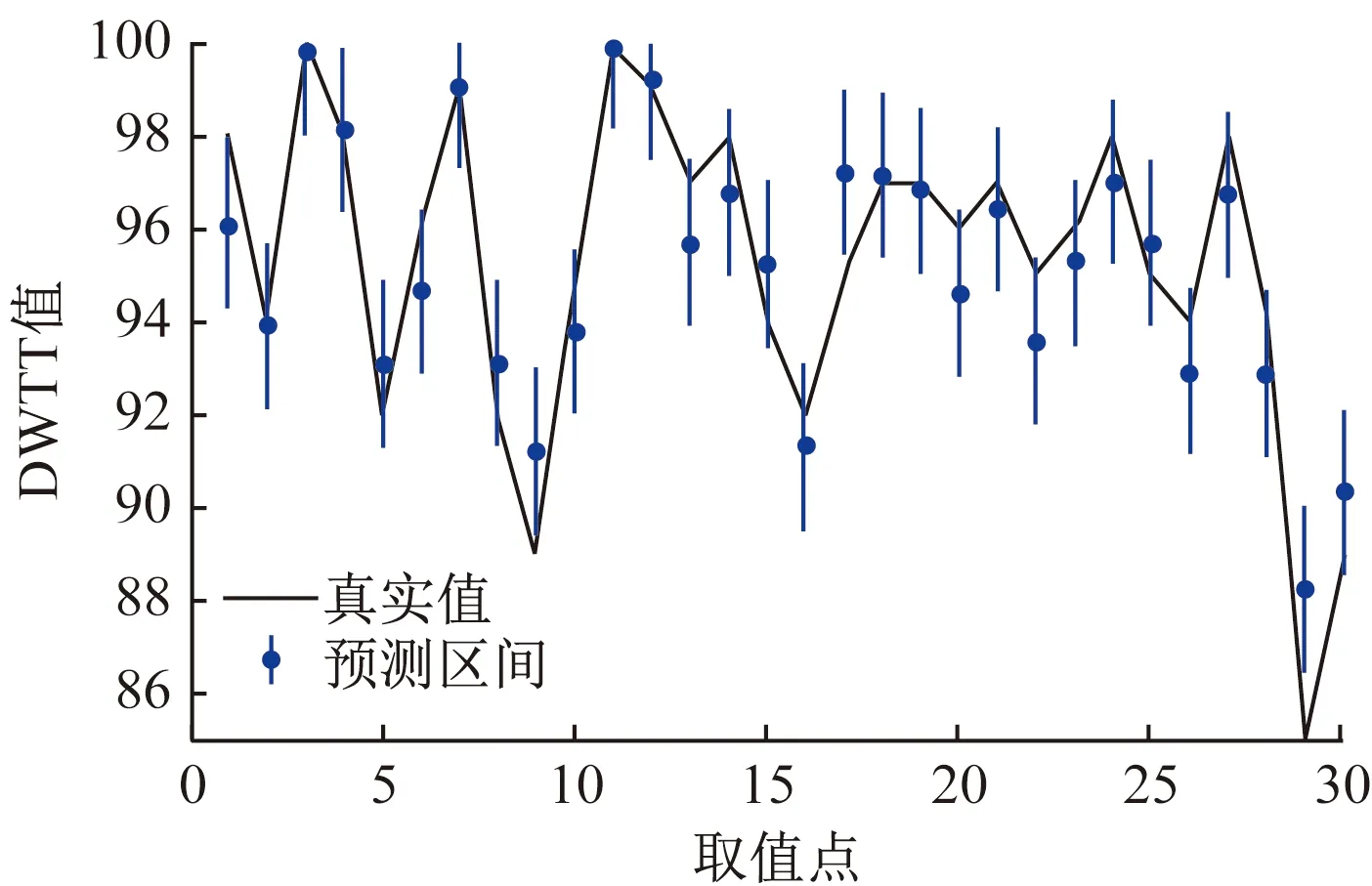
图7 准确率为80%时DWTT真实值和模型预测的区间值
1.3 其他工艺评估模型
同样地,采用区间估计的办法构建了头部和尾部抗拉强度、屈服强度、屈强比、断裂延伸率的评估模型,其r2和不同准确率下的Threshold如表4所示。
可以看到,单个的机器学习预测模型在性能上预测的准确率在训练集上并不太好,这也是本文引入区间估计的目的。4~14列为对应不同精度的区间范围值,实现了不同精度下的区间预测。
2 工艺设计模型
上一章中构建了工艺评估模型,它能根据影响对象钢种产品性能的20项主要因素来评估产品工艺性能,这章构建一个逆向的模型,即通过目标工艺性能和产品规格、化学成分来设计最优温度参数,具体来说就是通过如下参数来设计最优的6项温度参数:出炉温度、开轧温度、终轧温度、冷速、开冷温度、终冷温度,使用的方法是通过下节提出的自定义权重的模拟退火算法和第二章构建的评估模型。
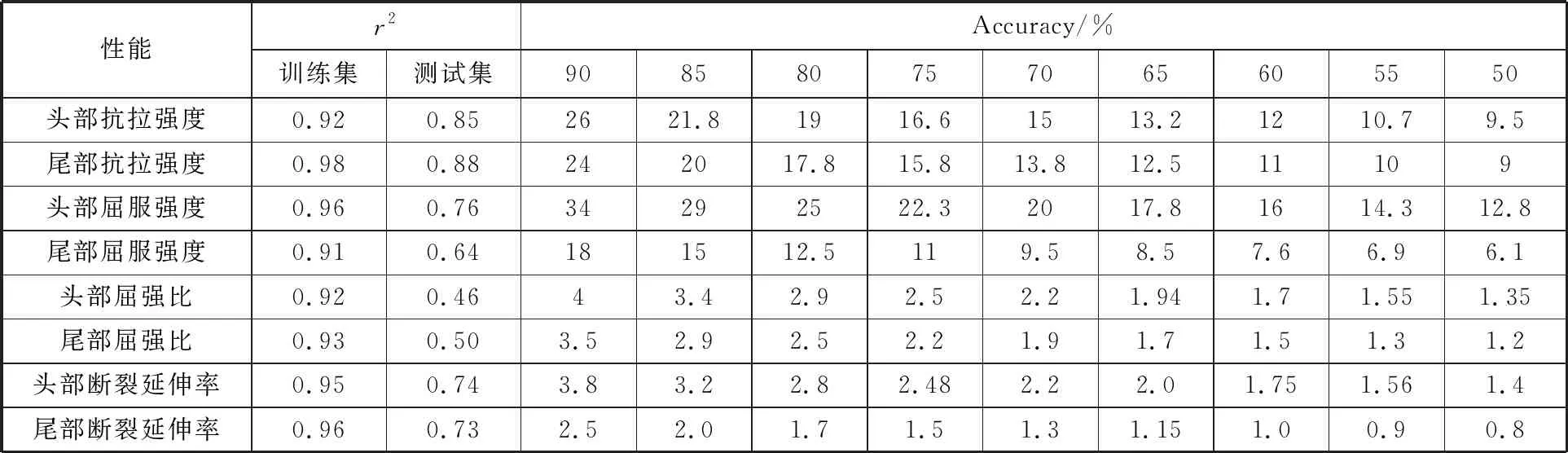
表4 工艺评估模型总结
(1) 工艺性能(9项):DWTT和头部尾部的抗拉强度、屈服强度、屈强比、断裂延伸率。
(2) 产品规格(3项):中间坯厚度、目标厚度、目标宽度。
(3) 化学成分(11项):C、Mn、Si、Nb、Ti、V、Cu、B、Cr、Ni、Mo。
2.1 自定义权重的模拟退火算法
模拟退火算法是一种解决无约束问题最优化的方法,它是通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最趋于全局最优的串行结构的优化算法[10],其流程如图8所示。

图8 模拟退火算法流程图
对目标函数E做如下修改,用以解决多目标优化的问题,假设E=(f1,f2,…,fn),以及一组自定义的权重λ=(λ1,λ2,…,λn),对给定x,定义:
E(x)=∑i(λi*fi(x))/S
(5)
式中:S=λ1+…+λn。设计模型中加入权重的意义在于设计人员可以通过调节权重来调节更加关注的性能。值得注意的是,算法的第 2,3 步随机生成的x2是在历史数据的最大值和最小值之间的随机数,保证最后的结果有意义。
2.2 工艺设计模型的构建
用x1表示3项产品规格和11项化学成分,用x2表示6项温度参数,同时y=(y1,…,y9)表示9项工艺性能,f1,f2,…,f9表示第二章中建立的9个模型,工艺设计的目标是对给定的x1和y寻找最优的x2,使得fi(x1,x2)与yi尽可能地接近,也即寻找x2使得di=|fi(x1,x2)-yi| 尽可能地小,其中i取值从1~9。这样就是一个多目标的优化问题,对于给定的权重λ=(λ1,λ2,…,λn),定义:
(6)
这样采用上一节的自定义权重的模拟退火算法便能够找到最优的温度参数x2,使得预测值与真实值尽可能地接近。
在历史数据集上做试验的结果如下:随机选取某条生产数据,其中包括3项产品规格、11 项化学成分和9项如下的工艺性能参数 97、660、639、582、564、888.3、88.1、48、48,分别取λ为(1,1,1,1,1,1,1,1,1)、(1,2,3,4,5,6,7,8,9)和(9,8,7,6,5,4,3,2,1),用此模型做试验,温度参数的真实值和3组预测值如表5。
由表5可以看到,对于不同的权重参数,模型寻找到了不同的冷却方案,经对比,试验一的结果和真实温度参数非常接近,这符合同权重下设计值应与真实值一致的预期;试验二、三根据侧重的性能不同,设计了多样的冷却方案,这对工艺设计和新产品的开发具有一定的辅助意义,能够在一定程度上降低新产品的研发成本。同时需要提高的地方是在模型中加入更多的约束条件,从而使其设计的温度参数更有意义。

表5 工艺设计模型试验结果
3 结语
本文首先以一种微合金高强钢为例,建立了9个工艺评估模型,它能根据20个工艺参数预测不同精度下头尾抗拉强度、屈服强度、屈强比、断裂延伸率和DWTT所在的区间。它基于本文自主开发的概率区间估计算法,该算法综合了机器学习的回归模型和历史数据的统计特征,能够实现精准预测。同时本文建立了工艺设计模型,它能够根据9项目标性能和3项产品规格以及11项化学成分设计最优的6项温度参数,使得产品在此工艺设计下的性能尽可能地接近目标性能。此模型基于本文自主开发的自定义权重模拟退火算法。
通过这两类模型达到产品质量预报和优化工艺设计的目的,从而能够辅助工艺评定和新产品的工艺开发。据我们查文献所知,这两种方法都是开创性的。本文后续的工作是重点考虑参数意义,对模型中的优化问题加入约束条件,使工艺设计模型中的冷却参数更有意义。

