体积分数可控的三维连续复合材料模型设计

韩慧敏 陈亮 聂雅琪

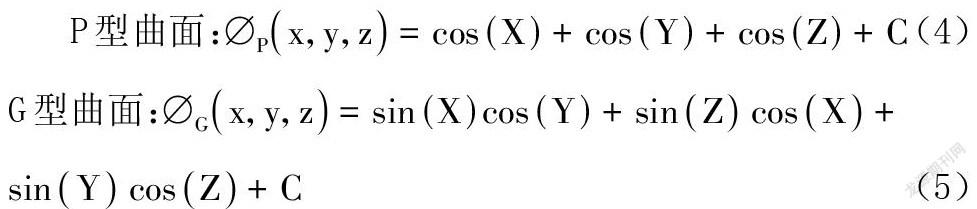
摘 要：提出一种具有体积分数可控的三维连续复合材料模型的构建方法，该构建方法是基于三重周期极小曲面（TPMS）结构，并运用空间分割策略能够精准地控制各个组成材料的三维空间分布及体积分数。与传统复合材料相对比，通过3D打印制造出来的具有各组分体积分数可控性的连续复合材料，能够提高连续复合材料的韧性、塑性、硬度等。

关键词：连续复合材料;TPMS;体积分数;3D打印

中图分类号： TB33

Abstract： A construction method of three-dimensional continuous composite model with controllable volume fraction is proposed in this paper. The construction method is based on the triple periodic minimal surface （TPMS） structure and uses the spatial segmentation strategy to accurately control the three-dimensional spatial distribution and volume fraction of each component material. Compared with traditional composites， continuous composites with controllable volume fraction of each component manufactured by 3D printing can improve the toughness， plasticity and hardness of continuous composites.

Key Words： CCMM;TPMS;Volume fraction;3D printing

1 研究現状

连续复合材料是由两种或以上不同材料组成，各材料所占的体积分数对连续复合材料的韧性、塑性、硬度等有着重要的影响，国内有很多学者对此进行了研究。邱昆等[1]运用有限元方法分析了新型非晶合复合材料的韧性和强度特性受颗粒体积、颗粒间距等的影响，实验结果体现了受到颗粒体积分数的提高以及颗粒间距缩小等其他因素变化，使得金属玻璃复合材料的韧性、塑性都有了显著的提升，尤其当体积分数为45%，复合材料的塑性得到了大幅提升，这些优化设计有利于制造出韧性更好的复合材料。

王敏等[2]分别制备出了不同碳纤维体积分数的CF/Al2O3-20%Ni金属陶瓷复合材料，其体积分数分别为0%、5%、10%、15%。通过控制碳纤维的体积分数，探究CF/Al2O3-20%Ni复合材料的硬度、抗弯强度、断裂韧性这3种性能的变化。实验展示了随碳纤维体积分数提升，复合材料硬度将会减小，而材料的断裂韧性和抗弯强度则先增加后减小，碳纤维体积分数达到10%时，断裂韧性和抗弯强度呈现最大值，与碳纤维体积分数为0%的样品相对比，分别提升了79%和134%，这说明了添加碳纤维后CF/Al2O3-20%Ni复合材料韧性、强度性能更加完善。研究结果表明了复合材料中各组分的体积分数的变化后，对材料的硬度、抗弯强度、断裂韧性等特性产生了很大的影响。

2三维连续复合材料模型构建

2.1给定基本特征的VDF计算

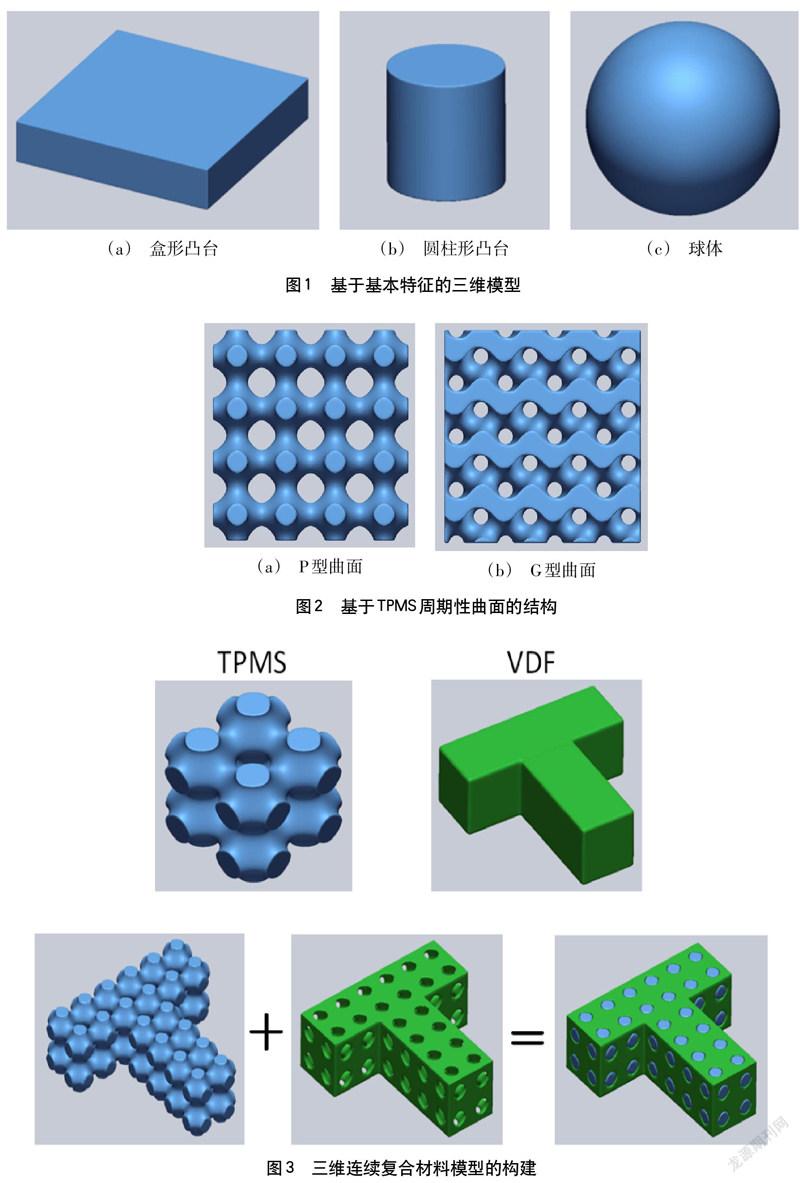
体积距离场（VDF）是一种有效的几何距离场形状的表示。更多详细的有关VDF计算和布尔运算的方法在早期的研究工作中有介绍[3-5]。以一个简单盒形VDF设计来举例子，通过运用以下算式来定义一个盒形凸台，详见图1（a）：

通过运用以下算式来设计一个简单的圆柱形凸台VDF，详见图1（b）：

球体的基本特征的VDF计算可以运用以下算式，详见图1（c）：

由于定义了基本特征，可以获得更多的从基础特征衍生出来的一系列复杂特征，并将这些复杂特征应用于三维连续复合材料设计中。

2.2 TPMS结构的连续复合材料模型

自然界或人造世界都广泛存在着TPMS结构，TPMS是一种三重周期极小曲面（平均曲率为0的曲面），在三维空间里其在3个维度的方向上都呈现出周期性规律的曲面。由于TPMS结构能够精准地表述各类物理材料（如连续复合材料、洗涤剂泡沫和硅酸盐等），受到了材料学家、物理学家、结构工程学家等的关注。此外，TPMS在三维空间内呈现多孔结构形态，在复合材料、人造器官、骨骼支架等领域具有较好的应用前景[6]。

TPMS 周期性P型和G型曲面，如图2所示，可由以下水平集近似方程式表示[3-5]：

所提出的连续复合材料三维模型是以TPMS结构为内部核心结构及VDF设计复杂外部形状。如图3所示。

3体积分数可控性研究

图4中（a）图所展示的是在曲面等值面为0时所构成的TPMS结构P型曲面，如若调整TPMS水平集近似方程式中等值面的值，即方程式中C的数值，将能获得如图4中（b）图和（c）图所示的不同的单元结构。从（b）图和（c）图可以发现，当等值面值C发生改变时，TPMS结构中被等值面所分割开的两个独立空间大小发生了变化。通过运用TPMS这一特点，提出连续复合材料体积分数的可控性策略。首先，被等值面所分割开的两个独立空间，我们可以认为其中一个空间作为连续复合材料中的材料A，而另外一个空间为材料B。然后，通过调整等值面值C，使得材料A和材料B的空间占比发生变化，从而实现精准地调节连续复合材料中各个材料的体积分数，如图5所示。

各个材料的三维空间分布是完全可控的，为广泛实际应用中复合材料的机械和物理性能优化提供了方法。所设计出不同体积分数的各类TPMS结构，能够构建出更加丰富的连续复合材料三维模型。最后，运用3D打印制造出不同体积分数的连续复合材料样品，如图6所示。

4 结语

与传统复合材料相对比，通过3D打印制造出来的具有各组分体积分数可控性的连续复合材料，能够提高连续复合材料的韧性、塑性、硬度等。通过简单地调整TPMS水平集近似方程中等值面值C，能够轻松、准确地构建出适用于特定应用需求的体积分数可控的各种三维连续复合材料模型。

参考文献

[1]邱昆，姜云鹏，史雪萍，等.新型颗粒增强金属玻璃复合材料的拉伸增韧机制[J].复合材料学报，2018，35（1）：124-131.

[2]王敏，贾建刚，郭铁明，等.碳纤维增强Al_2O_3-20%Ni金属陶瓷复合材料的制备及组织性能[J].复合材料学报，2017，34（12）：1-7.

[3]Huimin  Han， Dong-Jin Yoo， Liang Yan. Co-continuous Composite Material Design Using the Volumetric Distance Field Based on Analytic Shape Functions[J]. 哈尔滨工业大学学报：英文版，2019，26（1）：88-96.

[4]Jiho Kim，Dong-Jin Yoo. 3D printed compact heat exchangers with mathematically defined core structures[J]. Journal of Computational Design and Engineering， 2020（4）：4.

[5]Liang Yan ，Zhao Feng， Dong-Jin Yoo，Bing Zheng. Design of conformal lattice structures using the volumetric distance field based on parametric solid models[J]. Rapid Prototyping Journal，2020，26（6）：1005-1017.

[6]赵文英.基于极小曲面的骨支架力学及渗透性分析[D].大连：大连理工大学，2019.

3079500338256