基于IC卡数据的公交乘客下车站点推算模型

张志熙，陈玲娟

（武汉科技大学汽车与交通工程学院，湖北武汉430081）

0 引言

随着智能公交系统的快速发展，IC卡出行成为主流模式，采集乘客刷卡数据以及车辆到离站时间数据变得可行.挖掘公交IC卡数据与GPS数据，可有效提取公交乘客出行特征.利用公交乘客上车刷卡数据信息与公交车运行时间信息进行数据融合分析，可较为精确判断刷卡乘客的上车位置.但目前常规公交采用一票制，刷卡记录中缺失下车站点、换乘记录等信息.因此高效判断刷卡乘客下车站点，成为利用多源数据进行公交OD推导与换乘识别的关键.Barry等［1］以纽约市为例，对其公交系统存储的乘客信息进行研究，并基于出行链构造OD推断算法实现了下车站点的推导；Munizaga等［2］在高度匹配出上车站点的基础上，利用改进下车站点估计法，并结合均一时间系数法进行下车站点判断分析；Wang等［3］基于IC卡数据与GPS车辆定位数据，利用不间断出行法，提取乘客出行规律；Zhang等［4］基于智能卡、车辆定位、IC卡交易等数据，得出判断乘客下车站点的约束条件，并采用随机场模型和协同滤波算法提取信息缺失下的公交乘客出行链，从而实现下车站点判断；Yan等［5］在已有的OD矩阵基础上，利用K均值聚类将刷卡乘客分成规则和不规则两组，采用基于出行链的两步算法逐次识别乘客的下车站点；Jung等［6］利用一票制公交卡数据和土地利用特征开发了一种深度学习模型来估算公交乘客的下车目的地，并利用首尔AFC系统数据对模型进行检验；Kusakabe等［7］基于大坂市智能卡数据与交通调查信息，构建先验概率模型，研究公交乘客起讫点及下车时间.周雪梅等［8］利用公交线路周边的土地利用类型对出行者的下车概率建立模型分析；胡继华等［9］对影响乘客下车站点的因素进行分析，提出基于乘客个体特征的站点吸引权概率模型；翁剑成等［10］整合匹配公交IC卡和GPS等数据，提取出公共交通出行路线信息，建立基于个体出行数据的公共交通通勤出行链提取模型，挖掘乘客上下车信息；陈君等［11］根据公交乘客出行的时空规律性，提出基于通勤出行模式和关联出行模式判断下车站点的思路，并将当日出行信息和别日出行信息进行匹配来判断下车站点.

已有研究大多针对闭合出行链，或者只从站点本身吸引权、个人出行链或土地利用性质等单个影响因素出发推算公交乘客下车站点；出行距离（公交运行方向下游站点数），个人历史出行数据，各站点刷卡频次，乘客出行链类型等隐含因素的挖掘并未考虑.因此，本文分析乘客出行链类型，以刷卡大数据为基础，针对不同出行链提出基于公交站点下车概率的乘客下车站点推算模型，并构建模型检验方法.

1 公交出行行为及刷卡模式分析

1.1 出行行为分析

公交出行链可归纳为以下几种情况：

1）乘客多天连续出行，出行线路形成闭环，即换乘或者无换乘到达目的地后经过一段时间又从此地返回原来的起始位置.例如上班通勤、上学等规律出行，如图1所示，对应公交刷卡模式如1.2中1）和2）所述.

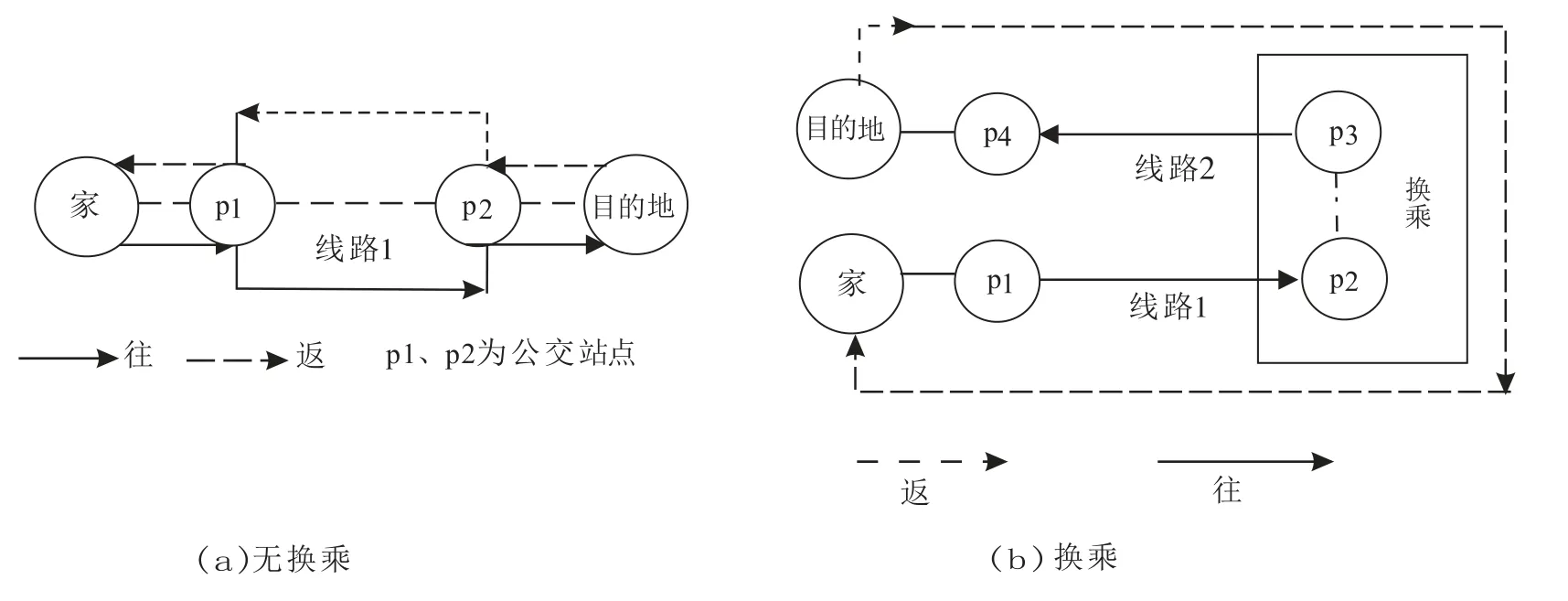
图1 有换乘和无换乘闭合出行链Fig.1 Closed trip chains of transfer and non-transfer

2）乘客多天出行只有半程处于连续状态，即某些天去往目的地时采用公交出行，返程采用其他方式；或某些天去往目的地采用其他方式，返程采用之前同线的公交，出行链半闭合，对应公交刷卡模式如1.2中3）所述.

3）乘客多天随机出行，呈现出完全非连续闭合状态，即在某地出发只搭乘一次公交再转移到另外的交通方式，亦或不返回等多种随机出行，具体过程如图2所示，对应公交刷卡模式如1.2中4）所述.

1.2 刷卡模式分析

无论闭合或非闭合出行行为，乘客在站间刷卡及上下车行为间表现出关联关系.已知上车站点，可以挖掘部分乘客出行规律和站点客流特征.对于完整闭合出行链，逐个连接乘客多次出行的上车站点可推算乘客下车站点；对于非闭合出行链，分析该乘客近段时间相似出行链来推算其下车站点.

针对各种不同出行链，连续两次刷卡间的连接方式分两种.本文作如下定义：在一条出行链中，相连两个公交刷卡点的连接称为一个公交接续节点，包括接续节点连续的上下车站和接续节点断裂的上下车站两种，具体分析如下：

1）假设乘客第i次刷卡记录在线路1的A站点上车，第i+1次刷卡记录在同线路站点B处，且B位于A下游，则站点B为第i次刷卡上车的下车站点，即接续节点连续，如图3所示.

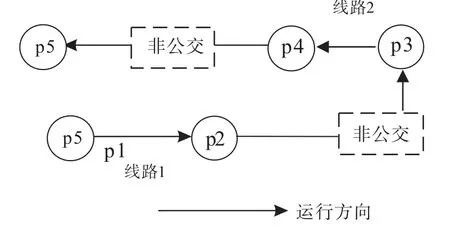
图2 随机出行Fig.2 Random travel

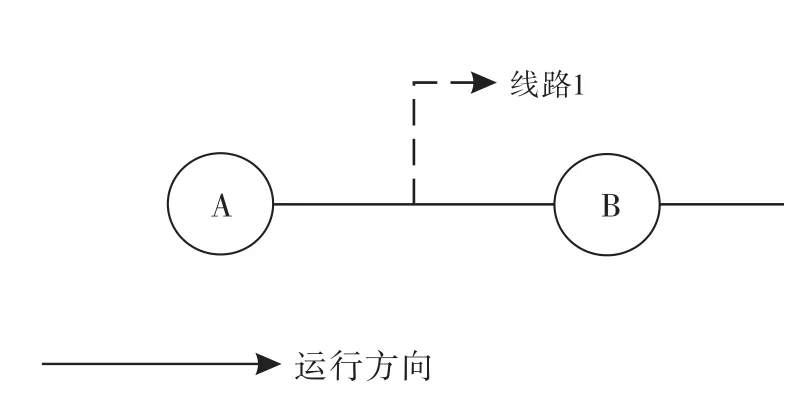
图3 无换乘接续节点连续Fig.3 Nodes continued without transfer

2）如果第i+1次刷卡记录的上车站点B与第i次的A不为同一条公交线，但B与A同线的下游站点B1满足距离阈值条件，仍然认为接续节点连续，即B也为第i次刷卡上车的下车站点，如图4所示.

步骤1）和2）为接续节点连续情况，针对接续节点不连续情况分析如下：

3）若第i+1次刷卡记录的上车站点B与第i次的A不为同一公交线，且不满足站点距离阈值条件，即接续节点断裂，则第i次刷卡上车的下车站点根据与A同线且位于下游的高频刷卡点来确定，如图5所示.

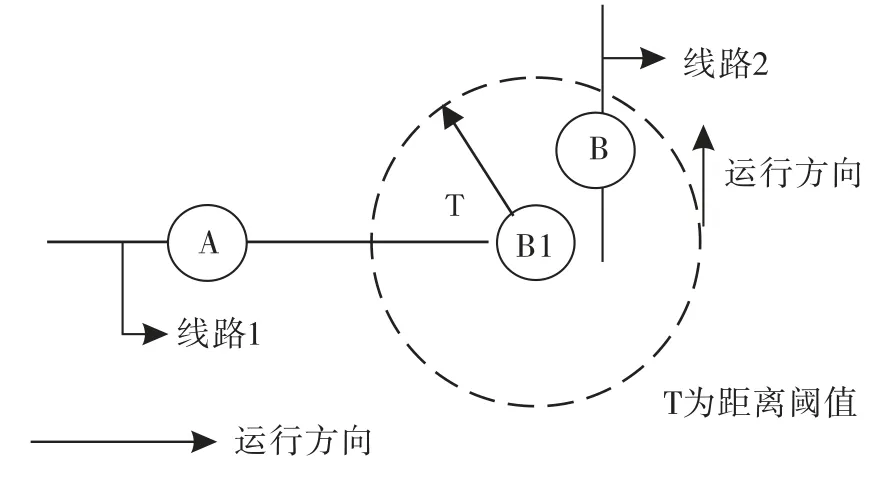
图4 有换乘接续节点连续Fig.4 Nodes continued with transfer

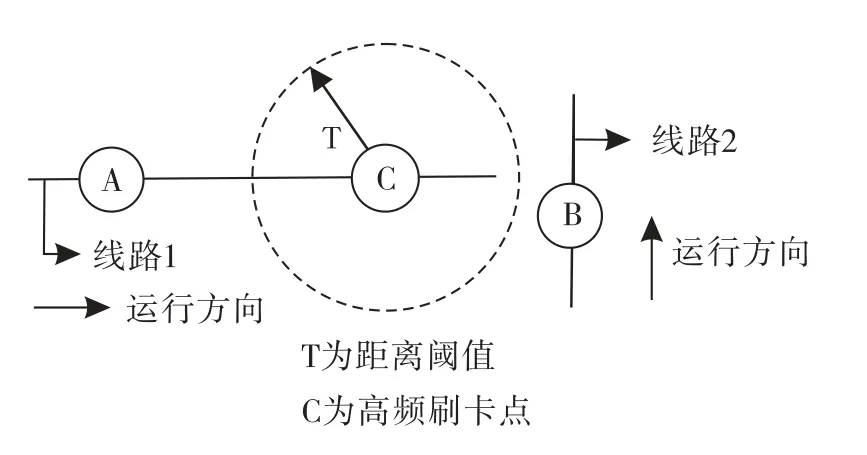
图5 接续节点断裂但有高频站点Fig.5 Existing high frequency stations with broken nodes

4）对于两次刷卡接续节点断裂且高频刷卡点集为空的情况，即无重复性的一般随机出行，则根据乘坐线路各站点的下车吸引权确定下车站点概率，如图6所示.

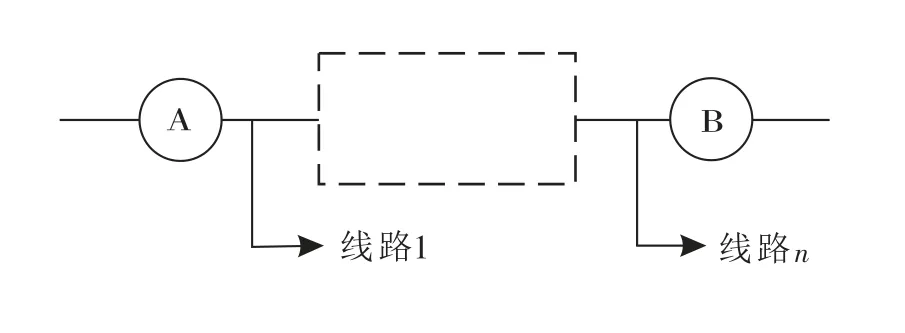
图6 接续节点断裂且无高频站点Fig.6 Stations with broken nodes and without high frequency

2 乘客下车站点估算

2.1 接续节点断裂的下车概率计算

对于出行接续节点连续情形，结合相应数据容易推断下车站点；对于接续节点断裂的情形，本文构建相应的乘客下车站点估算模型.

在接续节点断裂但高频刷卡点非空时（如图5），根据公交出行乘客一段时间的刷卡记录统计上车站点及频次Ni，若Ni≥N（N为高频站点设定阈值），则i为高频点，提取高频站点集I，用高频站点刷卡次数与总刷卡次数之比估算下车概率：

式中：Fi为高频点i的下车概率，Ni（i∈I）为高频点i的刷卡次数.

在接续节点断裂且高频刷卡点集为空时（如图6），假设某线路共有r个站点，Fij表示乘客在公交站点i上车在站点j下车的概率，则乘客在各站点下车概率矩阵F=[F]ij n×n.

以公交运营方向下游站点数、公交站点吸引权作为乘客下车概率的主要影响因素：

1）下游站点数的影响

参照现存研究文献［12］，设定乘客下车概率随公交运营方向下游站点数满足泊松分布规律，仅考虑下游站点数量，对在站点i上车的乘客，可得到其在不同站点的下车概率：

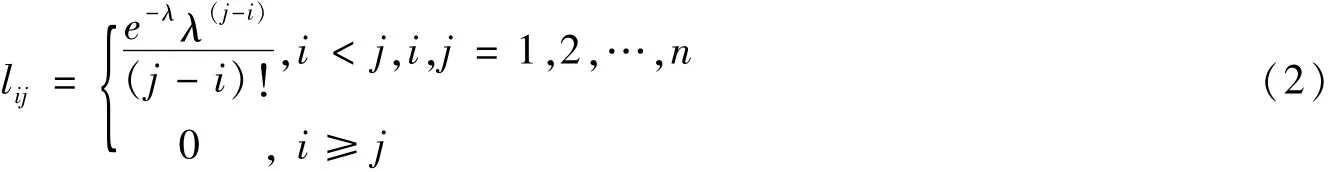
式中：lij为不同站点下车概率，λ为平均公交出行乘坐站点数量，如果站点i下游剩余站点数小于λ，则λ=n-i.

乘客乘坐公交站点数至少为1，至多为n-1，且各站乘车的一定会在后面站点全下车，由于初始泊松概率分布的和不一定等于1，故需对其做归一化处理：

2）公交站点吸引权的影响

在站点上车的人越多，表明其吸引行人的概率越大.由于公交出行重复往返性好，相同站点的发生吸引客流在总体上保持基本稳定，故根据IC卡刷卡数据中各站点上车人数可估算客流吸引权：

式中，Kj为站点j当次车辆上车人数，r为站点总数.

在综合考虑公交运营方向下游站点数、公交站点吸引权影响下，假设两主要因素对乘客下车概率影响权重因子为ρ（不同城市、不同公交线路的ρ值需经过敏感性分析决定），可得站点下车概率模型如式（5）所示：

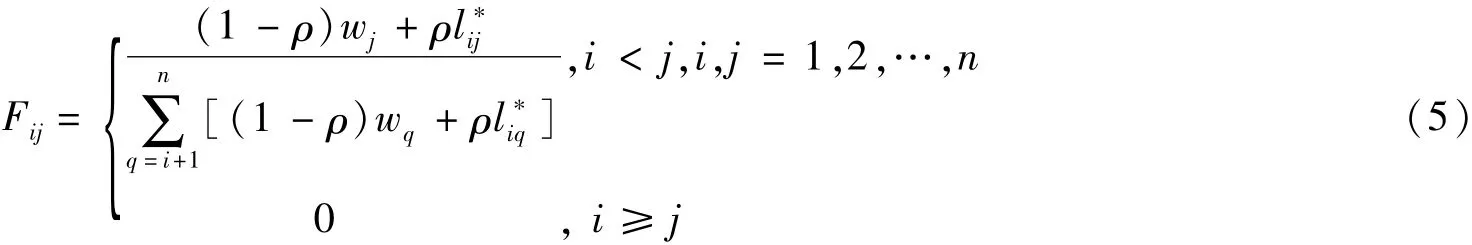
权重影响因子可根据实例中不同线路取不同值.

2.2 下车站点判断算法

基于IC卡大数据及出行链类型，推算下车站点，算法步骤如下：

1）读取乘客（同一刷卡ID）本次上车站点i的乘车线路R和下次刷卡站点i的上车线路R′；

2）若R=R′，且站点i′位于站点i下游，则可确定站点i′为上车站点i的下车站点；

3）若R≠R′，计算线路R下游站点i+k（1≤k≤n-i）与i′的最小欧式距离在i+k′站点取得，距离为d，若d≤T（给定阈值），则站点i+k′为下车站点；

4）若2），3）均不满足，则乘客出行接续节点断裂，根据刷卡ID统计出行记录，统计乘客各上车站点的上车频次Ni，判断上车站点下游是否有高频刷卡站点；

5）若高频站点集I非空，对每个具备高频点的卡号，计算Fi，将max（Fi）对应站点i作为该卡号的下车站点，同时集计所有具备高频点的乘客的高频站点下车总人数；

6）若高频刷卡站点集I为空，则根据车辆运行下游站点吸引权及概率分配得到下车站点，即利用式（5）中计算的Fij来分配下车站点，站点j处下车的人数统计可用式（6）求得，其中Ki为站点的上车人数，计算如下：

3 模型校验及实例分析

3.1 数据来源及参数设置

本文以青岛市11路公交连续一周全天乘客的IC卡数据为初始样本，进行下车站点识别.该路公交车共有17 535条刷卡记录，其公交IC卡存储信息的重要字段如表1所示.

表1 IC卡存储重要字段Tab.1 Important fields storing in a smart card

该线路共17站，统计该路乘客出行站数，得平均出行途经站点数为8.23，选定乘客平均公交出行途经站点数λ=9，算例中高频站点集的频次取值参照参考文献［9］.由于公交运行下游可能存在多个高频站点，为避免漏掉，定为不低于2次［9］，即Ni≥2.

对权重因子ρ，由于其是未知的，因此需要进行敏感性分析，本文试取0.1、0.3、0.4、0.5、0.6、0.7、0.9（每隔0.1取一个ρ值）等值进行敏感性分析，假设11路某位随机出行者在青岛大学上车，车辆往榉林公园方向运行，结合各站点历史上车人数数据，其在不同站点的下车概率如图7所示.

从图7可看出，ρ=0.1时最大可能下车站点为南京路，ρ=0.3、0.4时，最大可能下车站点为台东（婚纱街），而另外四个权重因子的最大可能下车站点均为镇江路，结果差别不大.同时，不同权值下各站点下车曲线走势基本一致，权重因子为0.3、0.4、0.5、0.6、0.7时曲线联系更紧密，但是从前四站下车概率情况来看，权重因子为0.5时计算概率相对更为合理，因此本次实例分析选取ρ=0.5.在推算其他线路下车站点时需要实地跟车调查重新标定参数.此外，由于城市主要城区内公交站点间距一般为500～700 m，因此本次实例分析选取500 m作为邻近公交站点距离阈值.

3.2 计算结果分析

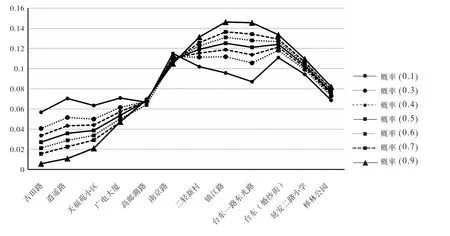
图7 不同权重因子下车概率Fig.7 Alighting Probability influenced by different weight factors

以11路为筛选字段处理原始数据，提取全天刷卡记录数据，再以司机卡号提取该辆车全天刷卡记录，并按乘客上车刷卡时间先后顺序排列.由于缺少公交GPS定位数据，利用高德地图并根据当地城市公交运行及发车状况，站间运行时间一般大于2 min（相邻两公交站间距一般为500～700 m，公交运行速度为15 km/h），到站停留时间一般小于2 min，按照刷卡时间间隔和对应公交车辆出发时间划分乘客上车次序，并对照线路图比对站点名，构建上车站点，提取乘客近期公交出行记录，识别出行链断裂的情形.

利用本算法判断下车站点记录共约17 400条，部分判断结果如表2所示，统计各站点上下车人数，抽取部分结果显示如表3所示.

表2 乘客下车站点推算结果Tab.2 Results of the passengers’alighting stop

表3 各站点刷卡乘客上下车人数Tab.3 Number of passengers getting on and off at each stop

3.3 结果检验

根据居民出行特征，居民日常出行会形成回路，即各个公交站点出行产生量和到站下车量在理论上应相等，并在误差范围内满足线性关系，相关系数R应该接近1，如式（7）：

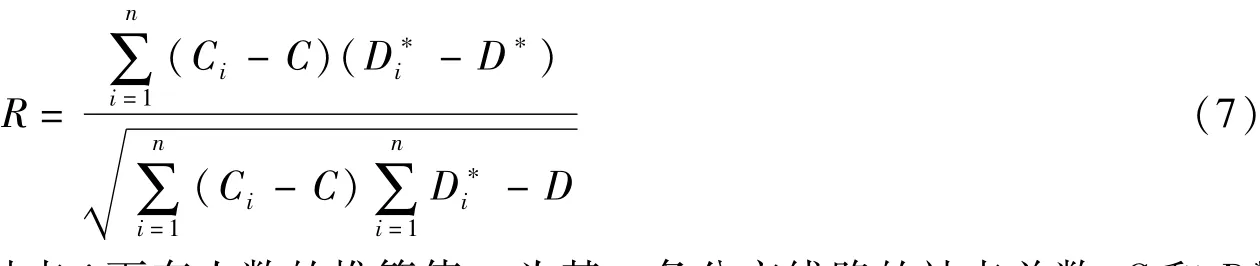
式中：Ci为在站点i上车人数为站点i下车人数的推算值，r为某一条公交线路的站点总数，C和D*分别为Ci和的平均值.

利用表3站点统计结果进行出行与吸引校验，得到回归分析结果如表4及图8所示.

回归结果显示公交站点全天刷卡乘客上下车人数相关系数为0.92，误差较小，说明本文推断各公交站点间刷卡乘客上下车人数基本平衡，符合公交刷卡乘客出行基本特征.校验回归方程系数为1.021 1，说明本文算法结果在集计分析层面较稳定，满足站点识别的精度要求，从而反映了本文算法模型推算下车站点的有效性和可靠性.

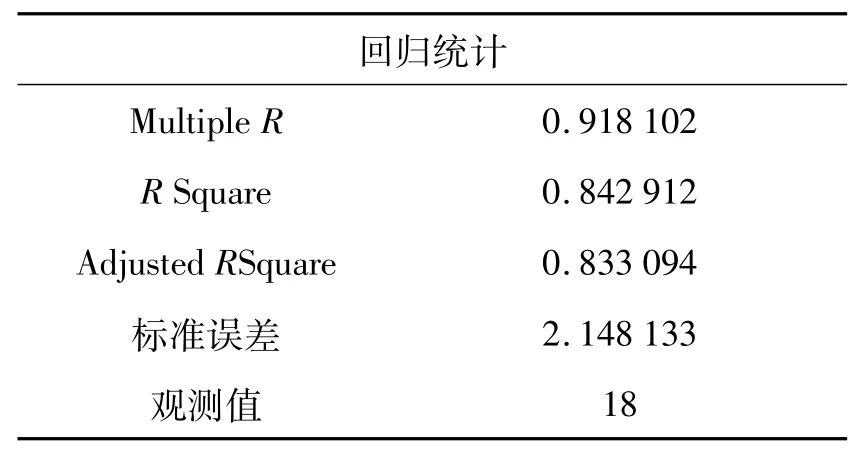
表4 回归统计参数Tab.4 Regression analysis parameters

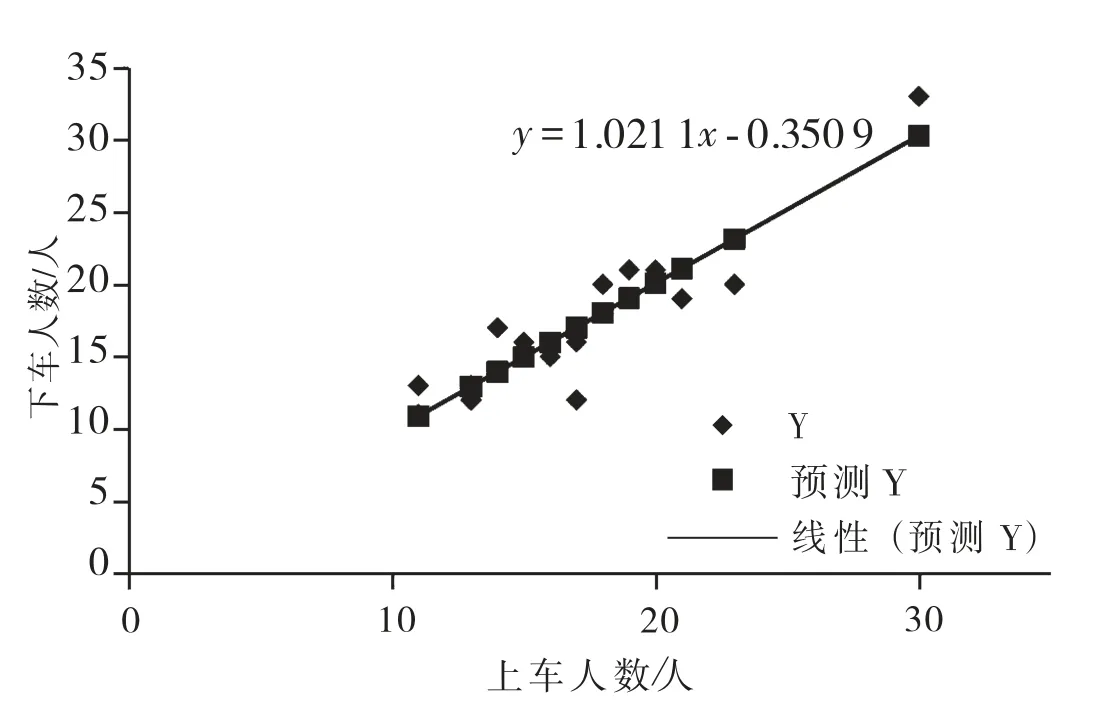
图8 回归分析结果图Fig.8 Regression analysis result

4 结语

本文首先对乘客通勤、随机出行等公交出行行为链、各类刷卡模式以及出行距离和公交站点吸引权等下车站点选择的影响因素进行了深入分析，分别构建各因素独立影响下的乘客下车概率计算公式；然后，融合各影响因素和出行特征提出了基于公交站点下车概率的乘客下车站点推算模型，并利用某线路实际数据对推算模型进行了验证；最后，利用青岛市11路公交数据进行了实例分析.结果表明，本文提出的算法模型能对不同出行链的公交乘客下车站点实现有效推算，对获取公交出行OD，提高公交运行效率，科学布局线路具有一定的理论与现实意义.

本文模型的数据来源为IC卡刷卡数据，相关参数标定也主要依靠刷卡数据，不包括投币和手机支付的乘客出行数据，与实际的下车人数推算存在一定误差.此外，受限于数据取样时间与成本，本文仅以一条公交线路为实验对象，未充分融合多条公交线路以及地铁刷卡等数据.下一步研究将考虑更丰富的、更贴近实际的出行模式，利用多源数据，提高下车站点推算模型的精度和适用性.