基于CFD的直翼推进器水动力性能研究及参数影响分析

史俊武，丁 晨，刘爱兵，杨文凯

（上海船用设备研究所，上海200031）

0 引 言

直翼推进器（如图1 所示）是一种安装有直翼型桨叶的特种推进器，其转轴垂直于船体设置。桨叶与推进器转轴平行，沿转轴旋转过程中产生推力。通过控制桨叶运动的偏心率和偏心方向，可使直翼推进器在垂直于转轴平面内产生任意方向和大小的力，从而实现对船舶的推进和操纵功能[1-2]。直翼推进器独特的工作特点使其广泛应用于猎扫雷舰、科考船、拖船、渡船等对操纵性能要求较高的特种船舶。

直翼推进器水动力性能与其推进效率和结构安全性息息相关，水动力分析是直翼推进器设计的前提和基础。直翼推进器和常规螺旋桨的推进型式和工作机理不同，其桨叶的运动特征和水动力性能相比螺旋桨更加复杂。自上世纪三十年代以来，直翼推进器水动力理论和实验研究工作在一些国家开展，出现了多种理论计算模型和方法，典型的包括谷口中提出的基于动量定理的准定常流动模型[3-4]，多国学者后来在此方法基础上也进行了相应改进[5-6]。近年来，随着计算机技术和计算流体力学的发展，众多学者开始通过数值方法对常规螺旋桨水动力性能开展仿真分析[7-8]，也为直翼推进器水动力特性的研究开辟了新的途径。

本文以某型直翼推进器的缩比试验模型为研究对象，利用CFD 方法对其进行了建模与仿真，对不同工况下的流场特性、敞水性能、桨叶载荷等水动力特性进行了研究，并针对不同桨叶结构参数对推进性能的影响进行了比较分析。

图1 直翼推进器Fig.1 Configuration of the cycloidal propeller

1 直翼推进器工作原理

直翼推进器工作过程中，桨叶以圆周速度ω绕转盘中心转动的同时，以速度V沿船前进方向运动，其合成运动轨迹为图2所示的摆线。图中N0点为桨叶转轴合成速度法线的交点，也即为转盘的速度瞬心。

图2 桨叶运动轨迹Fig.2 Motion trajectory of a propeller blade

在桨叶驱动机构的作用下，每片桨叶在随转盘转动的同时，也在绕各自转轴摆动。桨叶垂线与极轴的交点N称作控制点，控制点的偏心距与桨叶旋转半径之比定义为控制点的偏心率e。当控制点位于速度瞬心处时，桨叶弦线始终与来流方向一致，此时桨叶攻角始终为0，桨叶不产生推力。当控制点的中心距大于速度瞬心半径时，如图3 所示，除在0°和180°位置外，桨叶弦线始终与来流方向形成攻角，遂使桨叶产生升力L，其前进方向的分力LX即为推力。桨叶升力与阻力对桨转盘中心的合力矩即为桨叶转矩q。

直翼推进器的主推力为各桨叶旋转一周的平均主推力的叠加，即

式中，LX(Φ)为桨叶在转盘转角Φ时的主推力，z为桨叶数量。同理，推进器转矩可表示为

图3 桨叶推力的产生Fig.3 Thrust generation on the propeller blade

将主推力及转矩无因次化，可得主推力系数KT、转矩系数KQ及推进效率η分别为

式中，ρ为水的密度，n为推进器转速，D为桨叶回转直径，L为桨叶长度，J为进速系数。

2 直翼推进器计算模型

2.1 几何模型

本文以某型直翼推进器的缩比试验模型为研究对象，试验模型参数见表1。

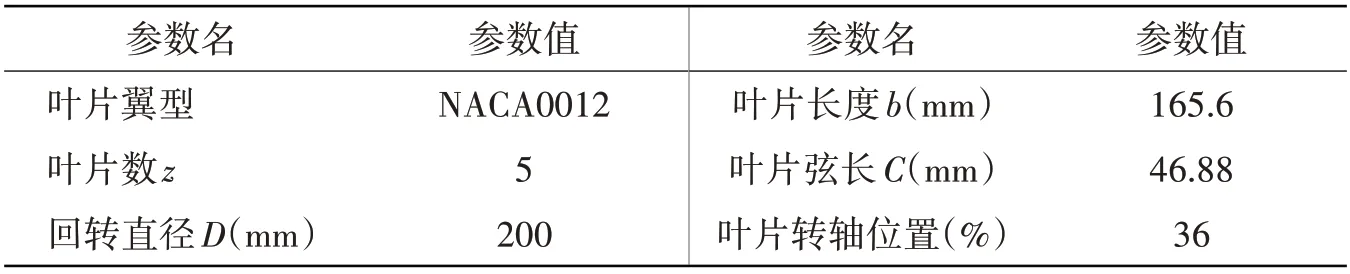
表1 缩比试验模型主要参数Tab.1 Main properties of the reduced-scale test model

2.2 计算域和网格

直翼推进器流场计算域分为外域和内域两部分，如图4所示。内域以推进器转轴为中心，直径为1.5D（D为桨叶回转直径）；外域为推进器外围立方体区域，长度与宽度为10D，深度为2D。此外，在内域中，以各叶片转轴为中心，设置直径为2.25C（C为桨叶弦长）区域为叶片域。

计算域网格划分中，内域和外域之间、叶片域和内域交界面采用滑移网格，既能实现既定运动又能节省计算资源[9]。同时，由于叶片在转动的同时自身摆动，其流动为非定常流动，且在某些方向角时叶片处于深度失速状态，因此需要采用高质量网格捕捉流场细节。为此，叶片周围采用结构化网格划分并适当加密，其他计算域采用非结构网格以简化网格划分过程。网格划分结果如图5所示。

图4 流场计算域Fig.4 Division of computational domain for flow field model

图5 计算域网格划分Fig.5 Mesh division of computational domain for flow field model

2.3 湍流模型与边界条件

本研究采用剪切应力输运模型（Shear Stress Transport Model，简称SST 模型）作为湍流模型。SST模型集合了k-ε和k-ω模型的优点，在近壁面区域采用k-ω，湍流耗散较小，收敛性好。在湍流充分发展的区域采用k-ε模拟，计算效率高，对复杂流场适应性更好。

边界条件设置中，进口、底部边界、左边界和右边界设为速度入口，出口为压力出口，上边界为壁面。

3 计算结果与分析

3.1 压力云图与速度云图

图6分别给出了偏心率e=0.6时不同进速系数下直翼推进器某截面的压力云图和速度云图。

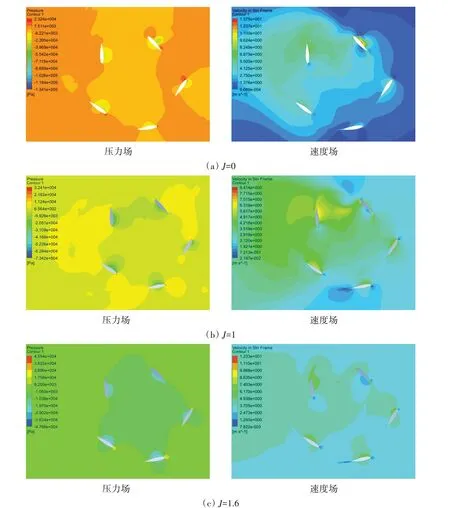
图6 直翼推进器CFD仿真云图Fig.6 Pressure and velocity contours of calculated results

从压力云图可以看出，在桨叶运动规律的控制下，叶片在前半圈（图3中180°～360°）和后半圈（图3 中0°～180°）时压力面、吸力面互换，产生的推力都指向航行方向。而且，进速系数越低，叶片的压力差越大，桨叶产生的推力越大。

从速度云图中可以看出，来流经前半圈叶片作用后速度增加，经后半圈叶片再次作用后加速向后流出。进速系数越低，叶片诱导的向后流速越大。同时可以看出，流场高速区偏向于0°～90°、270°～360°区域，这是由于该区域叶片攻角相对较大引起的。

直翼推进器的叶片因与水流两次作用而提高了推进效率。同时，后半圈的叶片会与前半圈的叶片的泄出涡相互作用，使得叶片的受力更加复杂化。

3.2 敞水性能

图7给出了上述缩比直翼推进器试验模型直航工况下不同偏心率时的水动力CFD 仿真结果和相应的敞水性能曲线。

从图中可以看出，在一定的偏心率e下，随着进速系数J的增加，推力系数KT与转矩系数KQ持续减小。偏心率增大，推进器产生正推力的进速系数范围随之变大。进速系数一定时，随着偏心率的增大，推力系数KT与转矩系数KQ也随之增大。

同时，偏心率一定时，推进效率η随着进速系数J的增加呈先增大后减小的趋势，且增大的趋势比减小的趋势缓，并在较大进速系数处达到峰值。随着偏心率的增大，正效率的进速系数范围增大，推进器的最大效率也随之增高。但在进速系数较低时，推进效率随着偏心率的增大而减小。因此，对于直翼推进器，可以通过偏心率的调节，实现不同工况下的推力与效率的最大化。

此外，从图中可以看出，数值仿真结果与试验数据的变化趋势一致且符合性较好，误差控制在9%以内，从而验证了本研究中所采用的建模方法的准确性。

图7 敞水性能曲线Fig.7 Comparison of calculated and experimental open water characteristics

3.3 单桨叶载荷

图8 为随转盘旋转过程中，无因次化后单叶片的主推力系数KLX、侧推力系数KLY以及绕桨叶转轴的转叶力矩系数KMZ的变化曲线。从图中可以看出，叶片载荷随着转盘转角的变化以360°为周期变化。随着进速系数的增大，叶片载荷也随之减小。

对于主推力系数，当桨叶位于0°和180°时主推力系数为0，在300°附近主推力系数达到最大值，此时桨叶攻角最大。而且前半圈叶片主推力系数明显大于后半圈，这是由于来流经前半圈的叶片诱导作用后速度增加，致使后半圈的叶片与水流作用的攻角减小引起的。侧推力系数在一个周期内正负交变，当桨叶位于120°和240°附近时分别达到正向和负向最大。整桨多叶片侧推力的叠加将使船体产生横摇，成对安装旋向相反的推进器则可抵消横摇的效果。转叶力矩系数变化规律与主推力系数相似，在300°附近达到最大值。

叶片载荷的波动幅值和周期是叶片强度校核的依据。

图8 单桨叶水动力载荷Fig.8 Hydrodynamic loads of propeller blade

4 桨叶主要结构参数对推进性能的影响

为研究直翼推进器主要结构参数对水动力性能的影响，本文以前述缩比试验模型为研究对象，运用CFD 仿真分析方法，就桨叶数量、桨叶弦长、叶厚、桨叶转轴位置等主要结构参数对推力系数KT、转矩系数KQ、推进效率η及推力波动幅值AMT等推进器水动力性能的影响进行了分析。

4.1 桨叶数量

图9为不同桨叶数量对水动力性能的影响分析结果。分析中，桨叶弦长不变，叶片数量分别选取3～6片。从分析结果可以看出，推力系数与转矩系数随着叶片数量的增加而增大，但后者增大率更大，因此推进效率随着叶片数量的增加而减小。但在进速系数较低时，叶片数量对推进效率的影响较小。从图9（d）可以看出，叶片数为5时推力波动幅值最小，6叶次之，3叶最大。因此，综合考虑推力与效率因数，5叶桨和6叶桨的直翼推进器的推进性能较优。

图9 桨叶数量对水动力性能的影响Fig.9 Hydrodynamic characteristics with different blade number

4.2 桨叶弦长

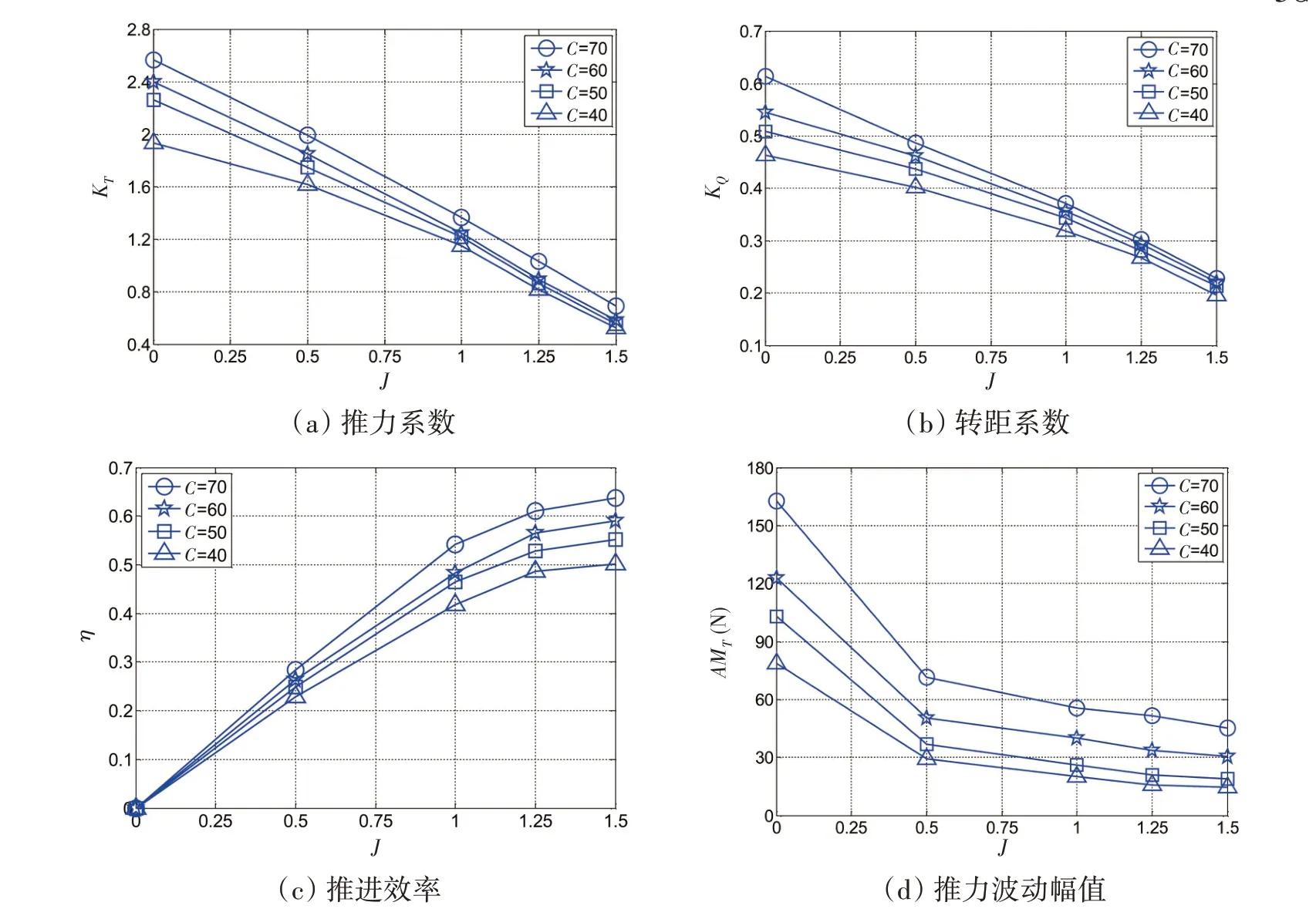
图10 桨叶弦长对水动力性能的影响Fig.10 Hydrodynamic characteristics with different blade chord length

4.3 桨叶厚度

叶厚对水动力性能的影响分析中，桨叶截面采用NACA 对称截面，截面最大厚度在0.3倍弦长处，桨叶相对厚度t/b分别选取0.10、0.12、0.15、0.18。图11 为分析结果，从图中可以看出，叶厚对主推力大小的影响较小，在低进速系数区域，相对厚度为0.12 和0.18 时推力较大。转矩随叶厚的增加而减小，在较低进速系数时尤其明显，因此推进效率随着叶厚的增加而增加。同时，随着叶厚的增加，主推力的波动幅值逐渐变小。从分析结果可以得出，相对厚度为0.18的桨叶综合性能较优。

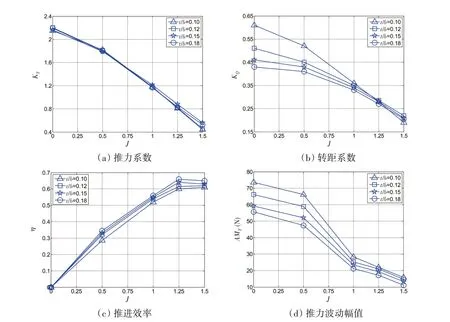
图11 桨叶厚度对水动力性能的影响Fig.11 Hydrodynamic characteristics with different blade thickness

4.4 转轴位置

图12 桨叶转轴位置对水动力性能的影响Fig.12 Hydrodynamic characteristics with different blade shaft position

图12 为桨叶转轴位置分别为20%、30%、40%、50%、60%弦长时的水动力分析结果。从图12（a）中可以看出，进速系数较小时，转轴位置靠前时推力较大，而进速系数较大时，转轴位置靠后时推力较大。从推进效率角度看，如图12（c）所示，桨叶转轴位置在30%弦长时推进效率最高，40%和50%弦长位置次之，20%弦长位置推进效率最低。推力波动方面，从图12（d）中可以看出，转轴位置在桨叶弦线中部靠前时，推力波动幅值较小。综合各因素考虑，桨叶转轴在30%弦长附近时推进器性能较优。

5 结 论

本文介绍了直翼推进器的工作原理，以某型直翼推进器的缩比试验模型为研究对象，利用CFD方法进行了水动力建模与仿真，得到以下结论：

（1）对直翼推进器CFD 仿真方法进行了研究，对计算域网格划分方法、湍流模型及边界条件的设置等计算前处理进行了分析，并通过将数值仿真结果与试验数据的比较，验证了所采用仿真方法的准确性。

（2）通过数值模拟，得到了直翼推进器的流场特性云图、敞水性能曲线，以及单桨叶的水动力载荷系数曲线，为直翼推进器流场特性分析、水动力性能预报、桨叶及推进器机构强度校核提供了依据。

（3）通过仿真的方法，就桨叶数量、桨叶弦长、桨叶厚度、转轴位置等主要结构参数对水动力性能的影响进行了分析，确定了桨叶主要结构参数的取值范围，为桨叶结构设计提供了帮助。