带前置定子导管桨非定常力特性计算分析

王 磊，唐登海，刘登成

（中国船舶科学研究中心，江苏无锡214082）

0 引 言

本文研究的带前置定子导管桨由环状导管、定子和转子组成，具有推进效率高、激振力低、临界航速高等优势[1]，该类型推进器常用于潜器、AUV等水下航行器、鱼雷和潜艇等。

与敞开式螺旋桨相比，带前置定子导管桨由于转定子时刻处于相对运动之中，因而不可避免会产生非定常力，加之推进器运行于船艉的非均匀尾流之中，这使推进器受到的非定常力更加复杂。推进器非定常力一方面通过轴系激励船体艉部产生振动，另一方面还直接辐射噪声，干扰航行体有效执行任务。因此，有必要对带前置定子导管桨的非定常力进行研究，以便为设计低激振的带前置定子导管桨提供依据。

针对带前置定子导管桨的研究，目前大多集中于其定常水动力性能，非定常力研究尚有一定的局限性。在势流理论研究方面，王国强[2]使用升力面-面元耦合方法计算了带前置定子导管桨的定常水动力性能；刘小龙[3]使用面元法计算了带前置定子导管桨的非定常性能，但未对非均匀来流对推进器非定常力特性影响规律进行计算分析。随着计算机性能的提高和CFD 技术的进步，采用求解RANS方程等粘流方法对带前置定子导管桨进行性能预报和流场计算成为可能。潘光[4]使用RANS 方法对后置定子的导管螺旋桨进行了定常数值模拟，得到了其敞水特性曲线；洪方文[5]对带前置定子导管桨进行了单流道定常计算，得到了转定子表面的定常压力分布特性；刘登成[6]对带前置定子导管桨进行了定常数值预报，研究了导管间隙对导管桨时均水动力性能的影响；饶志强[7]对均匀来流下泵喷推进器非定常力频率进行了理论推导，分析了转定子叶数与非定常力频率的关系，并采用RANS 方法进行了非定常计算，结果与理论推导吻合良好；张志荣等[8]对带前置定子导管桨的梢隙流动进行了数值模拟，发现梢隙流动中存在4 种类型的涡结构。在实验研究方面，舒礼伟等[9]在循环水槽中对带前置定子导管桨导管脉动压力进行了实验测量，得到了脉动压力在导管周向和轴向的分布规律；Suranarayana[10-11]对轴对称水下航行体后泵喷推进器开展了水动力和空泡性能实验研究。

本文采用CFD 商用软件Fluent 对带前置定子导管桨非定常力特性开展研究。首先计算9 阶来流下P4119桨的非定常力，验证所用计算方法的准确性，在此基础上以非均匀来流周期数和转定子叶数为自变量，系统地制定了计算方案，使用RANS 方法和滑移网格技术对带前置定子导管桨进行了非定常性能模拟，并使用快速傅里叶变换的手段提取转子非定常力的频域信息，分析转子的非定常力与非均匀来流及转定子数目的关系。

1 数值计算方法及验证

本文采用RANS 方法计算推进器非定常性能，为了对所采用数值计算方法的准确性进行验证，选取P4119 桨为计算模型，如图1 所示。P4119 桨是ITTC 确定的一个螺旋桨标准模型，被广泛用于螺旋桨性能研究和CFD计算结果验证。美国泰勒水池的Jessup[12]曾通过实验测量了P4119 桨在3、6、9、12周期的非均匀来流下所受到的非定常力。本文对9 周期非均匀来流下P4119 桨的非定常力进行了计算，所用的P4119 桨的尺寸与实验相同，其直径D为304.8 mm。

本文采用商业软件Fluent 进行数值计算，动量方程对流项采用二阶迎风格式离散，扩散项采用中心差分格式离散，压力-速度耦合采用SIMPLE算法，湍流模式选择SSTk-ω模型。

计算域为一个与螺旋桨共轴的圆柱体，进口位于桨盘面上游3D处，出口位于桨盘面下游10D处，圆柱体直径为10D。计算域划分为外部的静止域和螺旋桨周围的旋转域。网格划分如图2所示，静止域采用结构网格划分，网格数为277 万；旋转域采用4 面体非结构网格划分，网格数为131 万，第一层网格的y+在20-200范围内。

边界条件设定为：进口和外围圆柱面均定义为速度入口，出口定义为压力出口，物面为无滑移壁面，静止域与旋转域的交界面设置为interface，采用滑移网格技术处理桨的转动，螺旋桨转速为600 r/min。

图1 P4119桨Fig.1 Propeller P4119

图2 静止域（左）和旋转域（右）网格Fig.2 Grids of stationary domain(left)and rotational domain(right)

非均匀来流在进口处通过PROFILE定义，其平均速度为2.54 m/s。非均匀来流只有轴向分量，径向分量和切向分量为零。轴向分量具有明显的九周期特性，图3 给出了9 周期非均匀来流的无量纲速度Vx/Vin（以平均来流速度无量纲化）沿周向的分布。

计算时先采用多参考系（MRF）方法进行定常计算，收敛后以定常计算得到的结果为初值，进行非定常计算，时间步长为0.000 25 s，即每个周期包含400 个时间步，每个时间步螺旋桨旋转0.9°，共计算1 200 步，即螺旋桨旋转3 周。图4 给出了计算结果与Jessup实验结果的对比，可见计算结果与实验结果吻合较好。

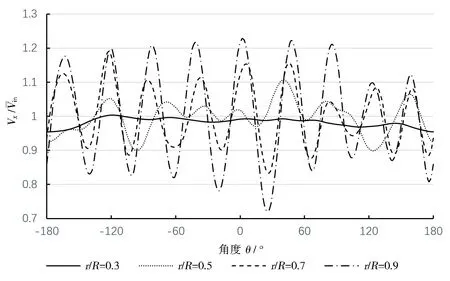
图3 九周期非均匀来流的速度分布Fig.3 Velocity distribution of the ninth-harmonic incoming flow

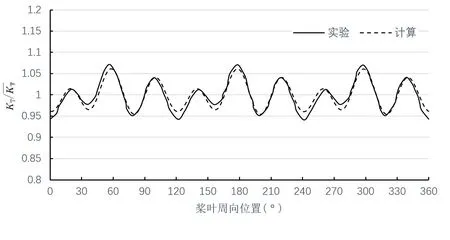
图4 P4119桨非定常推力系数计算结果与实验结果的比较Fig.4 Comparison between calculated and measured unsteady forces of P4119 propeller

2 带前置定子导管桨非定常力特性分析

2.1 研究对象

图5 带前置定子导管桨Fig.5 Ducted propeller with a pre-swirl stator

本文的研究对象是一个带前置定子导管桨，如图5所示。导管长为119 mm，定子弦长为39.4 mm，转子直径D为200 mm，0.7 半径处螺距比（P/D）0.7R为1.274 9，转子与导管之间的间隙为1 mm。

带前置定子导管桨转子非定常力主要是由于船艉非均匀尾流和定子尾流的影响而产生的，对船艉非均匀流场进行傅里叶分析，发现尾流场中包含不同周期数的脉动量，加之定子尾流的影响，导致转子进流场周向不均匀。这样，在转子叶片旋转过程中，进流大小和攻角均是周期性变化的，结果导致转子受力也是周期性变化的。本文主要研究带前置定子导管桨转子非定常力与非均匀来流周期数和转定子叶数之间的关系，为此设计了包括多个工况的计算方案，如表1 所示。对于不同工况，通过改变来流平均速度来保证带前置定子导管桨的总推力系数相同。

表1 带前置定子导管桨计算方案Tab.1 Calculation proposals with different parameters

2.2 计算方法

计算域为与导管桨共轴的圆柱体，进口位于导管进口上游3D处，出口位于导管进口下游10D处，圆柱体直径为10D。计算域划分为3 部分：外部流场域、定子域和转子域，前两者为静止域，转子域为旋转域。

网格采用混合网格。对于外部流场域和定子域划分H 型结构网格，如图6所示，对于转子域采用四面体非结构网格划分。定子域和转子域均划分单流道网格。定子、转子和导管表面均划分边界层网格，第一层距壁面约0.2 mm，y+在10-110范围内。推进器各部分网格如图7所示。

图6 外部流场域网格分布 Fig.6 Grid distribution of outer domain

数值离散方法、湍流模式及边界条件设置与P4119 桨非定常力计算一致，其中转子转速设定为1 800 r/min，各阶轴向非均匀进流分量以周向正弦分布形式定义，具体表达式为

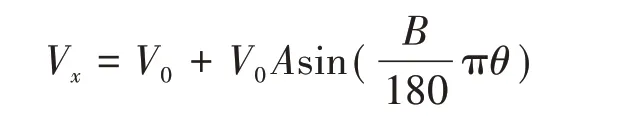
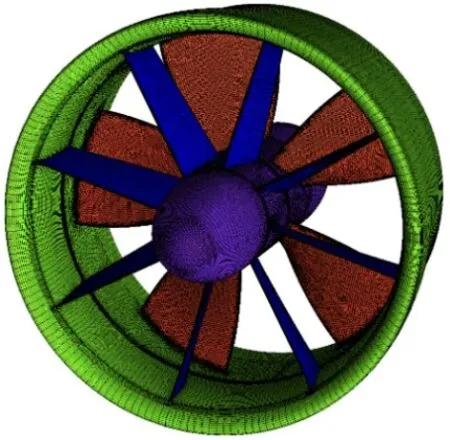
图7 带前置定子导管桨表面网格Fig.7 Surface grid of ducted propeller with stator

式中，V0为轴向速度分量均值，A（A= 0.1）表示轴向速度脉动幅值，B表示指定的进流周期数，θ为周向角度，范围为0°～360°。非均匀进流的径向和切向分量为零。

计算时首先使用MRF 方法进行定常计算，收敛后以定常计算的结果为初值进行非定常计算，非定常计算的时间步为8.333 33E-5 s，即每个周期包含400 个时间步，转子每步旋转0.9°，计算1 200 步即转子旋转3周。

2.3 计算结果与分析

2.3.1 不同周期数来流下带前置定子导管桨转子非定常力特性分析

为了研究非均匀来流周期数对带前置定子导管桨转子非定常力的影响，选择转子数为6，定子数为8 的导管桨进行研究，计算了4、5、6、7、8、11、12、13 周期非均匀来流下转子的非定常力。当来流周期数为6 时，转子推力系数在一个周期内的变化如图8 所示，呈现明显的6 周期特性。对其进行傅里叶分析，结果如图9所示，纵轴为相对幅值，即转子推力脉动量幅值与推进器总推力平均值的千分比。结果表明，转子推力在叶频处出现明显的峰值，其它频率处的幅值可以忽略不计。

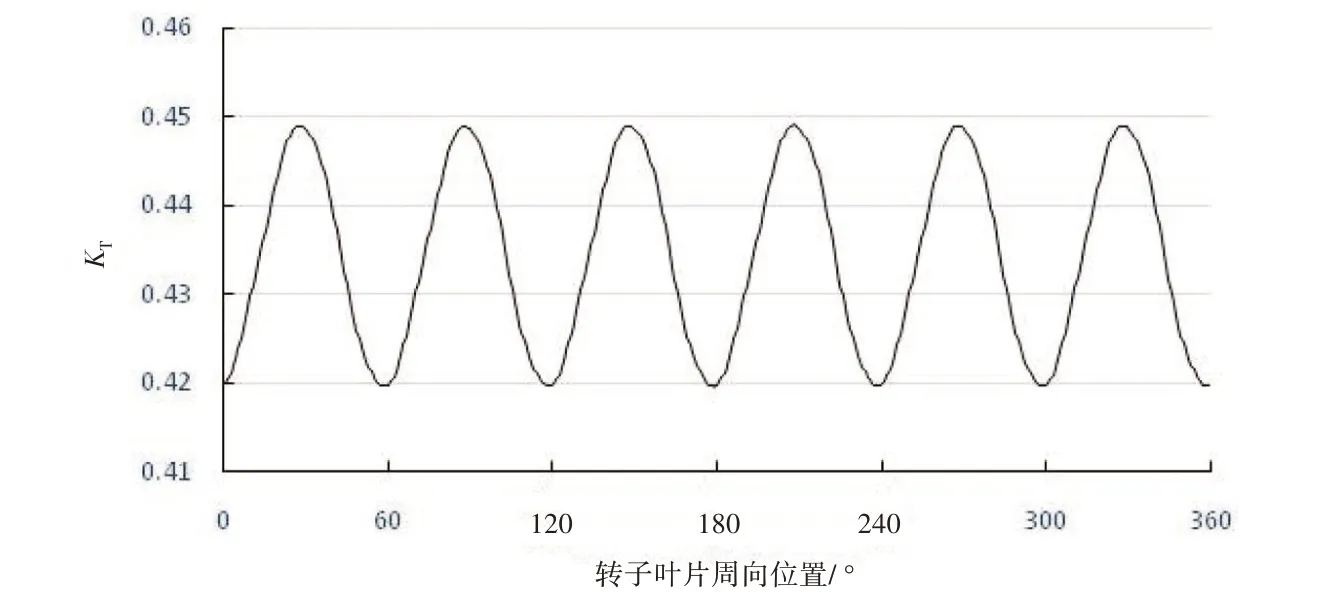
图8 六周期来流下转子非定常推力系数计算结果Fig.8 Calculated unsteady thrust coefficient of rotor in sixth-harmonic incoming flow

图9 六周期来流下转子非定常推力FFT分析结果Fig.9 Harmonic components of rotor thrust in sixth-harmonic incoming flow

对不同周期数非均匀来流下的计算结果，提取转子的三向非定常力，并进行快速傅里叶分析，表2为转子三向非定常力相对幅值。

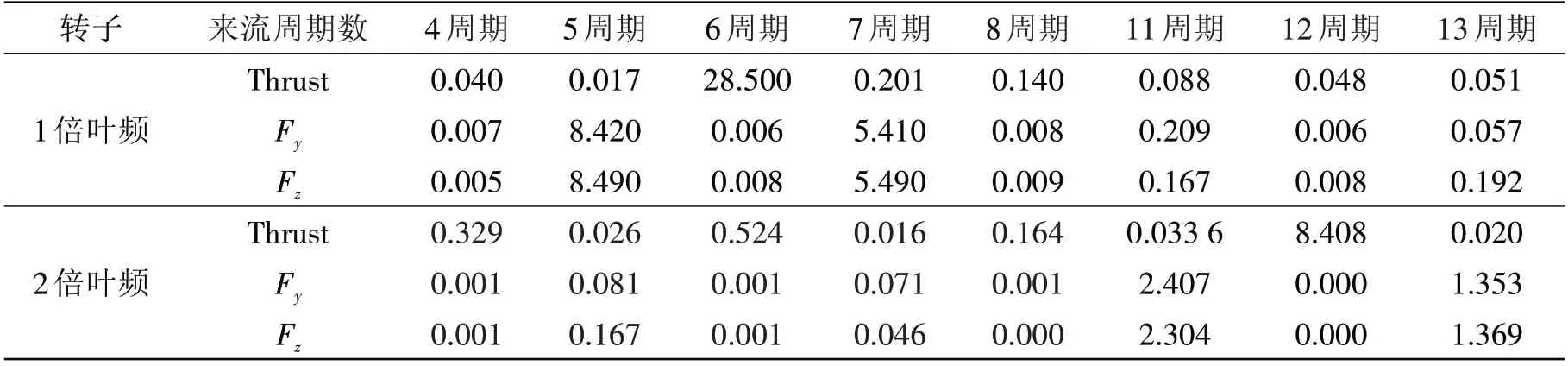
表2 不同周期数来流下转子非定常力相对幅值（单位：‰）Tab.2 Unsteady forces of rotor with different inflows(unit:‰)

可以发现，对于推力，6周期来流产生1倍叶频的非定常推力，12周期来流产生2倍叶频的非定常推力，其它工况下非定常推力可以忽略不计；对于侧向力，5 周期和7 周期来流产生1 倍叶频的非定常侧向力，11 周期和13 周期来流产生2 倍叶频的非定常侧向力，其他工况下非定常侧向力可忽略不计，这与螺旋桨的非定常力特性是一致的。由表2 还发现，7 周期伴流产生的转子非定常侧向力要小于5周期伴流产生的转子非定常侧向力，13周期伴流产生的转子非定常侧向力要小于11周期伴流产生的转子非定常侧向力，这是因为非均匀来流周期数越多，相邻伴流峰周向间距就越小，转子叶片相对于伴流峰的相对侧斜角就越大，导致非定常力幅值偏小。由于同样的原因，12周期来流产生的转子2倍叶频非定常推力小于6周期来流产生的转子1倍叶频非定常推力，11周期和13周期来流产生的转子2倍叶频非定常侧向力也小于5 周期和7 周期来流产生的转子1 倍叶频非定常侧向力。此外，还注意到，5、7、11、13周期来流各自产生的转子Y、Z两个方向非定常力幅值相同。

2.3.2 不同定子叶片数目时转子非定常力特性分析

为了研究转定子叶片数目对带前置定子导管桨转子非定常力的影响，选择转子叶片数为7，定子叶片数分别为6、7、8、9的导管桨进行研究。

由于前置定子会影响转子的实际进流场,进而影响转子非定常力，因此首先对转子进流场进行分析。以7 叶定子为例，计算均匀来流下导管+7 叶定子模型流场，取定子近后方流场作为转子进流场，对0.7R半径处的轴向速度进行傅里叶分析（R为转子半径），结果如图10 所示，纵轴为轴向相对速度的脉动幅值。由图可知，由于7叶定子的影响，转子进流场存在7、14、21等7的整数倍周期的脉动，其中7周期脉动幅度最大。除7的整数倍周期外，其它周期数的脉动幅度都很小。

对转子叶片数为7，定子叶片数分别为6、7、8、9 的导管桨，计算其在均匀来流下的非定常力，表3为转子非定常力相对幅值。

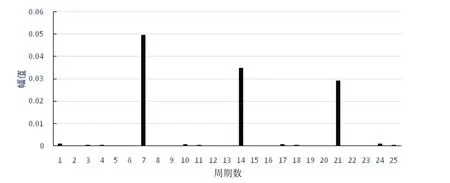
图10 转子进流场0.7R半径处轴向速度FFT分析结果Fig.10 Harmonic components of axial velocity of rotor inflow at 0.7R

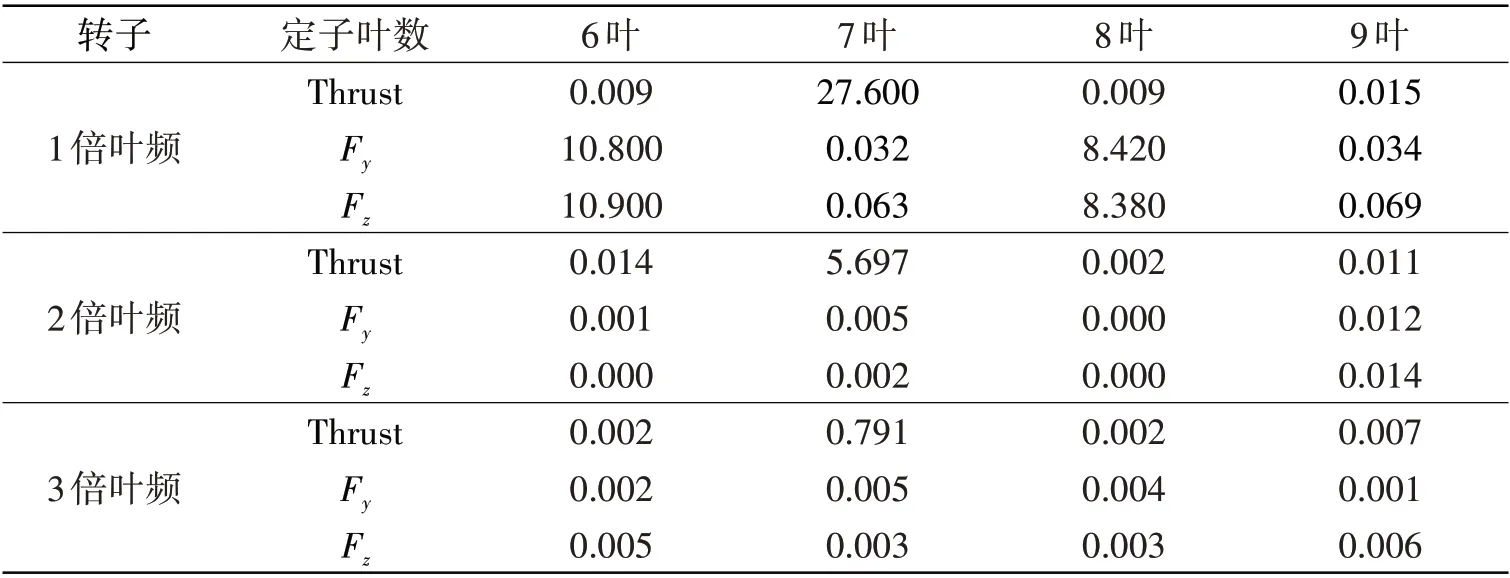
表3 不同定子叶片数目时转子非定常力叶频分量相对幅值（单位：‰）Tab.3 Unsteady forces of rotor blade frequency components with different stator blade numbers(unit:‰)

对于推力，当定子数为7 叶时，转子在1 倍、2 倍和3 倍叶频处均产生非定常推力，这是由7 叶定子产生的7、14、21周期尾流导致的，其它工况下转子非定常推力可忽略不计;对于侧向力，只有当定子叶数为6 叶和8 叶时，转子产生非定常侧向力，这是由6 叶和8 叶定子产生的6 周期和8 周期尾流所导致的。同时，由表3 中还可以发现，定子数为8 叶时转子的非定常侧向力要小于定子数为6 叶时转子的非定常侧向力，而这两种工况下各自的转子Y、Z两个方向非定常力的幅值是相同的。

2.3.3 非均匀来流和转定子叶片数目共同作用下转子非定常力特性分析

为了研究非均匀来流和转定子叶片数目共同作用下带前置定子导管桨转子非定常力特性，选择转子叶片数为7、定子叶片数为8的导管桨，计算其在5、6、7、8、9周期非均匀来流和均匀来流下的非定常力。表4为转子非定常力在叶频处的相对幅值。

表4 不同周期数来流下转子非定常力叶频分量相对幅值（单位：‰）Tab.4 Unsteady forces of rotor blade frequency components with different inflows(unit:‰)

对于推力，只有7 周期来流下转子产生非定常推力；而对于侧向力，表4 中各个工况下，转子均产生非定常侧向力，这是由于8叶定子产生的8周期尾流的影响。此外，5、7、9周期来流下转子非定常侧向力幅值与均匀来流下相同，说明此时转子侧向力是由于定子的作用产生的。对于6周期和8周期来流，此时转子同时受非均匀来流和8 叶定子产生的8 周期尾流共同作用，导致转子非定常侧向力与均匀来流下转子非定常侧向力不同。

3 结 论

本文以非均匀来流下的带前置定子导管桨为研究对象，计算了多种转定子叶数、不同周期数来流下的转子非定常力，并重点分析了转子非定常力的影响因素，得到了以下结论：

（1）CFD 计算结果表明，带前置定子导管桨转子的非定常力由转子进流决定，这与敞开式螺旋桨一致，但转子进流同时受到非均匀来流和定子尾流的影响；

（2）来流经过定子后，转子进流中会增加定子叶数整数倍周期的脉动；

（3）对于叶数为ZR的转子，设k为正整数，进流中的kZR阶脉动分量引起kZR阶非定常推力；

（4）对于叶数为ZR的转子，进流中的kZR±1 阶分量使转子产生kZR阶非定常侧向力，且kZR+ 1阶分量引起的侧向力幅度小于kZR- 1阶分量引起的侧向力幅度；

（5）对于叶数为ZR的转子，当进流中只存在kZR±1 阶分量中的一个时，转子Y、Z两个方向的非定常力幅度相同；

（6）为减小非定常力，设计带前置定子导管桨时，除了需要考虑非均匀进流的影响外，还要考虑转定子叶数相互适配，避免mZS=kZR和mZS±1 =kZR的转定子叶数组合出现（ZS、ZR为定子和转子叶数，k、m为正整数）。

本文计算了一系列工况下带前置定子导管桨转子的非定常力，但仅分析了转子的非定常力特性。对于定子和导管，二者实际运行于转子转动产生的周期性变化的流场之中，也会受到非定常力作用，其非定常力特性将在后续文章中进行分析。