水平面操纵运动中潜艇受到的“离面载荷”的数值模拟

潘雨村，谢志勇，周其斗

（海军工程大学舰船与海洋学院，武汉430033）

0 引 言

“离面载荷”（‘out-of-plane’loads）是最引人注目的潜艇水动力现象之一，它是指潜艇在水平面进行回转或者带有斜航漂角时，遭遇到的垂直面的受力和力矩。Feldman[1-2]和Mackay[3]是较早关注这一现象的学者。

尽管“离面载荷”（垂向力和俯仰力矩）通常要比对应的“面内载荷”（侧向力和艏摇力矩）小一些，但是它们对潜艇的机动性和稳定性却有着重要的影响。在回转过程中，“离面载荷”有时会在出其不意的情况下造成一个抬首角度。为了克服这一影响，操纵员可能需要将升降舵压几度舵角，但是这种压舵角的处理会进一步挤压有限的控制裕度[3]。因此，“离面载荷”的存在使得准确地控制潜艇进行水平面操纵运动成为一个具有挑战性的课题，尤其是当潜艇进行高速回转的时候[4]。

当潜艇在水平面内进行操纵运动时，指挥台遭遇横向来流，不仅会产生横向受力，还会在其梢部泄出强烈的旋涡。涡结构进一步向下游传输，并与艇体截面上的横向流动发生相互作用，这一相互作用不仅创造出非对称的复杂三维尾流，而且也是产生“离面”受力和力矩的来源。操纵运动中潜艇绕流的复杂性，是人们试图预报潜艇“离面载荷”时遭遇的主要困难之一。

为了研究这个复杂的流动现象，人们开展了许多试验研究。斜航试验和旋臂试验分别是获取“面内”位置导数和旋转导数的常规手段，但是在这些试验过程中，同样可以测量“离面”受力和力矩的信息。Roddy[5]对SUBOFF 潜艇模型开展了一系列的约束模型试验，测量了“面内”载荷和“离面”载荷。Roddy 指出，对于全附体的模型来说，试验结果证明“离面载荷”随着漂角的变化呈非线性的增长。Watt 等[6]对于Mark I 型潜艇模型进行了风洞和水池斜航试验，测量了包括“离面载荷”在内的大量数据。他们的结果和Roddy的结果类似，俯仰力矩随着漂角的变化也是呈现出非线性的增长。Fu等[7]利用粒子成像测速技术（PIV）对ONR Body1 潜艇模型定常回转运动中的绕流场进行了描述，同时也对“离面载荷”进行了测量。

随着计算流体力学（CFD）技术的发展，人们也开始用CFD 方法来研究“离面”载荷现象。Mackay等[8]应用了CANAERO 面元法对潜艇后体的横流分离涡进行了模拟。潜艇模型在一定漂角下“离面载荷”的预报值同试验值吻合得很好。Sung等[9]对回转运动中的潜艇流场进行了数值模拟。在他的模拟中，ONR Body1潜艇模型遭遇了向下的受力以及抬首力矩。针对受力和力矩这两者来说，受力的预报值同试验值吻合得更好。

在本文中，采用数值方法对操纵运动中的潜艇模型遭遇的“离面载荷”进行了预报。定常和非定常的RANS 方法分别被用来模拟SUBOFF 模型的斜航拖曳试验和旋臂试验。对两种情况下的“离面”受力和力矩进行了比较，对两种情况下潜艇绕流的流动特征也进行了讨论。

1 数学模型

船体周围的流动采用不可压缩的雷诺平均的Navier-Stokes方程（RANS）进行模拟：

采用定常RANS 求解器来模拟斜航拖曳试验，对于旋臂试验则采用非定常RANS 求解器来模拟。许多学者采用在随船坐标系中求解Navier-Stokes 方程的方法来模拟船舶回转运动。这种方法在处理网格和数值计算时比较方便，但是会遇到人工压力梯度的问题[10]。为了避免这个问题，本文中采用在惯性坐标系中求解N-S方程的方法来模拟潜艇回转运动。

对流项采用二阶迎风差分格式进行离散，而扩散项则采用二阶中心差分格式。对于非定常流动计算，时间导数项采用一阶向后隐式格式离散。压力-速度的耦合问题则采用了半隐式压力连接方程（SIMPLE）进行处理。为了封闭控制方程，需要采用合适的湍流模型。Sung[9]对比了几种湍流模型，认为realizablek-ε模型能够和试验数据较好地吻合。因此，本文也采用了这种湍流模型。

2 数值方法

2.1 模拟斜航拖曳试验的计算域和边界条件

本文的计算对象是全附体的SUBOFF 潜艇模型[5]。对于斜航拖曳试验，计算域是一个包围潜艇模型的长方体，如图1所示。入口边界位于潜艇上游1.5L处，进流速度为4 m/s（基于艇长的雷诺数为Re=1.693×107），压力出口边界位于潜艇下游3L处。在艇体表面采用不可滑移壁面边界条件。Roddy在多个漂角下对潜艇模型进行了测量试验，文中则是通过修改入口边界和侧面边界的横向速度来实现漂角的系列变化。

图1 模拟斜航试验的计算域示意图Fig.1 Schematic computational domain of oblique towing test

2.2 模拟旋臂试验的计算域和边界条件

对于旋臂试验的数值模拟，本文采用了圆柱域，它代表旋臂水池的外边界，外边界与艇体之间保持2L以上的距离。在外边界上采用静压开放边界条件，这样流动进入边界或流出边界都完全由求解的结果来决定，而不需要设置预定方向的流动进出[11]。船体表面则采用无滑移壁面边界条件。

如图2 所示，在本文的计算过程中，直接包围潜艇的一个内域（inner region）在每个时间步都会按照UDF（User Defined Function）的计算进行运动，那么中间层（intermediate region）的网格系统就需要适应内边界的变化，为此本文采用了基于光滑和重构的动态网格技术[12-14]来实现网格的变形。

在旋臂试验中，潜艇模型在每个航次都保持一个固定的线速度航行，而旋转半径和旋转角速度则在每个航次进行变化，这样就可以通过测量不同角速度下的艇体受力来推断旋转导数。在本文中，潜艇的切向线速度保持为4 m/s，而无量纲的角速度则在0.7 到0.02 之间变化，对应的旋转半径则从20 m到60 m之间变化。

图2 模拟旋臂试验的计算域示意图Fig.2 Computational domain of virtual rotating arm test

3 结果和讨论

为了考察网格敏感性，我们生成了粗、中、细三套逐渐加密的网格。在模拟斜航拖曳试验时，细、中、粗三套网格分别划分成14.36，7.83 和4.33 百万个单元；在模拟旋臂试验时，细、中、粗三套网格分别划分成13.41，7.15 和4.31 百万个单元。在细、中、粗三套网格中，贴近壁面的第一层网格的无量纲尺度y+分别为30，43和60。

3.1 受力和力矩

作用在潜艇模型上的“离面”受力和力矩分别用如下的公式进行无量纲化处理：

图3 绘出了在斜航试验中，艇体受到的垂向力和俯仰力矩随着漂角变化的曲线；图4 绘出了在旋臂试验中，艇体受到的垂向力和俯仰力矩随着角速度变化的曲线。这些曲线都体现出类似抛物线的特征。因此，“离面载荷”可以被拟合成带有二阶项的数学表达式，由此就可以得到对应的非线性水动力系数。表1列出了二阶水动力系数Z'vv、M'vv、Z'rr、M'rr。

总的来说，从粗网格到细网格，二阶水动力系数没有大的改变。Z'vv、M'vv的计算结果与试验值之间差异不大。目前没有在公开文献中找到SUBOFF 潜艇模型的Z'rr、M'rr试验结果，所以其计算结果暂时无法与试验值进行比较。

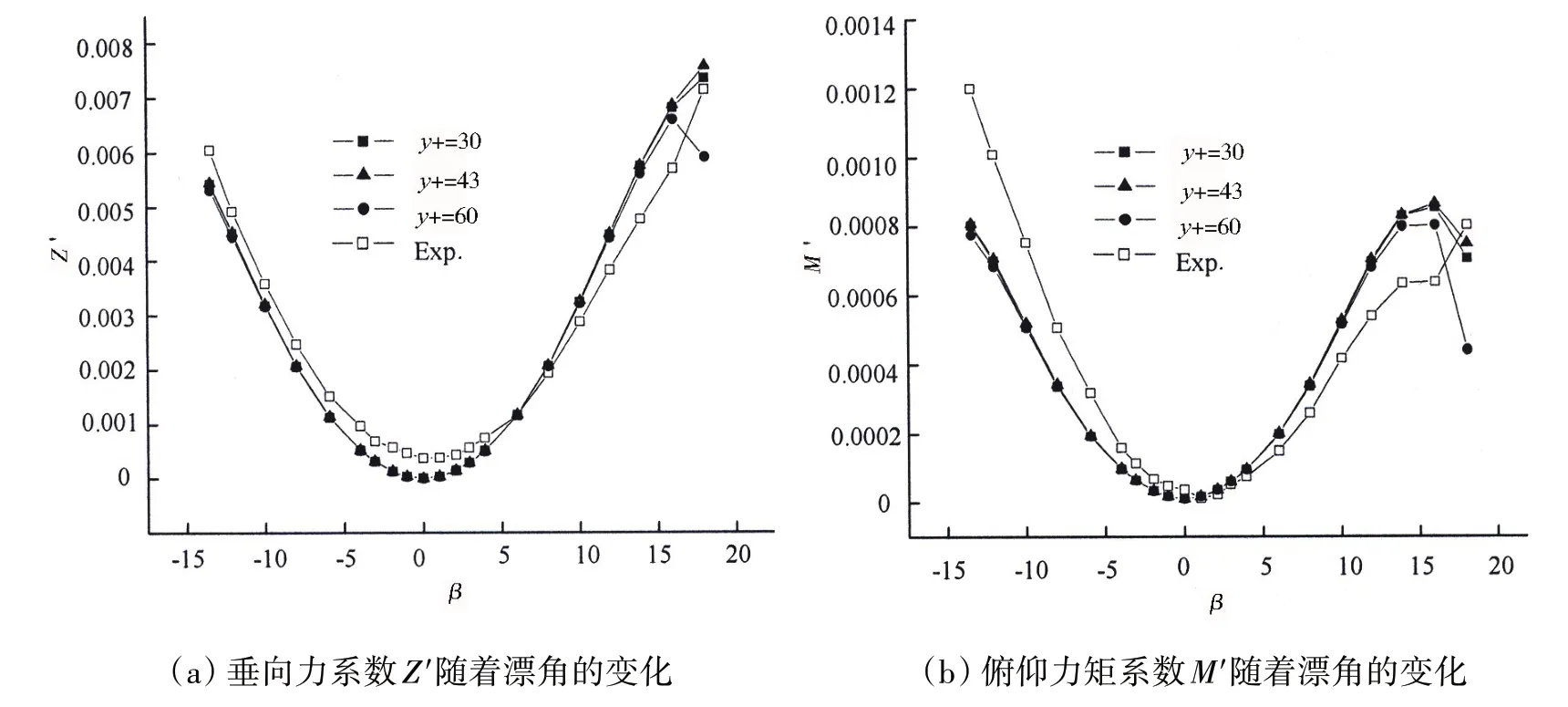
图3 垂向力系数Z'和俯仰力矩系数M'随着漂角的变化Fig.3 Normal force coefficient Z'and pitching moment coefficient M'varying with drift angles

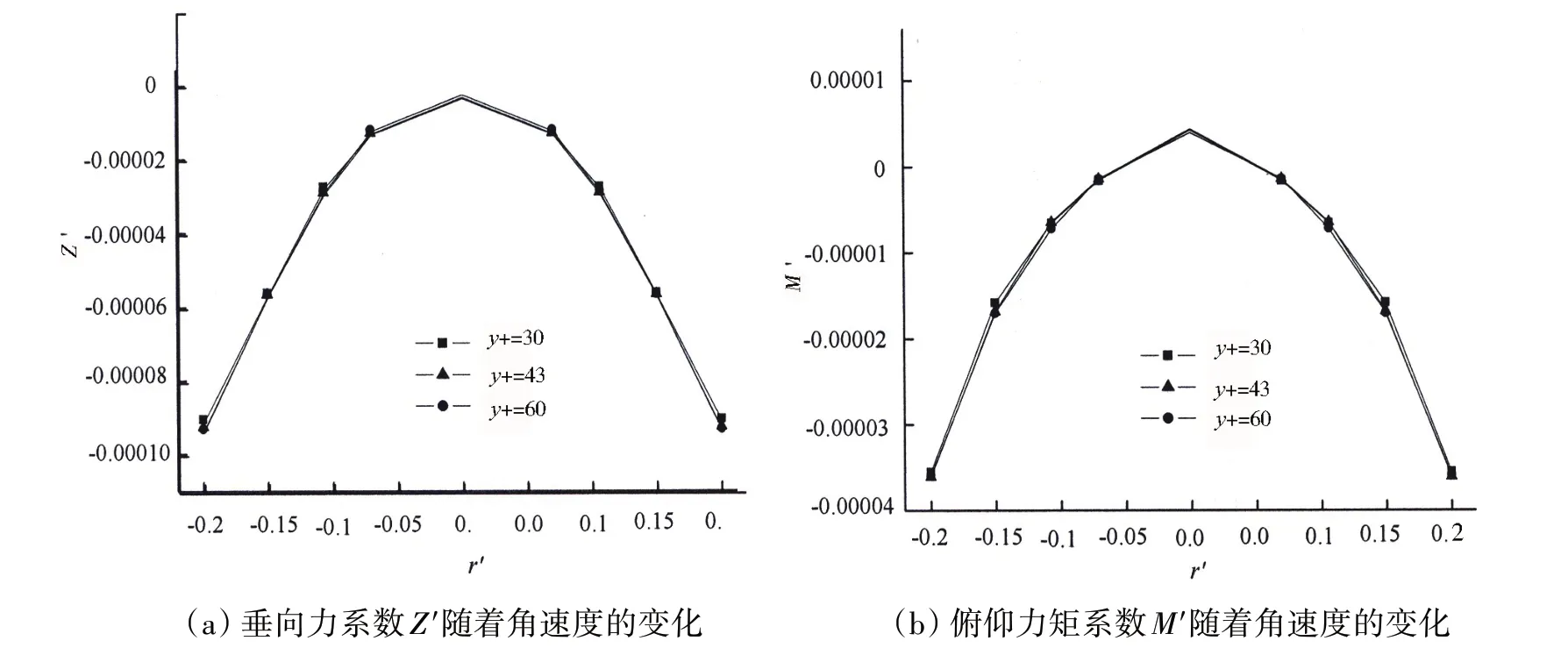
图4 垂向力系数Z'和俯仰力矩系数M'随着角速度的变化Fig.4 Normal force coefficient Z'and pitching moment coefficient M'varying with angular velocities

表1 SUBOFF潜艇模型在水平面的部分二阶水动力系数Tab.1 Second-order coefficients of the SUBOFF model in horizontal plane

在图3 和图4 中，也绘出了分别用细、中、粗三套网格计算出来的受力和力矩曲线。总的来说，三套网格得到的结果之间相差不明显。主要的差别在于，在图3（a）中，当漂角在16°左右时，用粗网格计算得到的垂向力的曲线达到顶峰，漂角进一步增大，垂向力开始下降；然而用中、细网格计算得到的垂向力曲线继续上升。在图3（b）中，当漂角大于16°以后，用细、中、粗三套网格计算出来的俯仰力矩曲线都开始下降，但是用粗网格计算得到的那条曲线要比另外两条下降得更陡峭。出现这一现象的原因可能是漂角大于16°后，用粗网格进行计算时，流动开始发生分离，而用较细的两套网格进行计算则没有发生分离。因此，可以认为是网格分辨率低造成了流动分离的过早发生。

另外，从图3可见，斜航试验中潜艇受到的垂向力和俯仰力矩的计算值与Roddy[5]的试验数据大体吻合。两者的差别就在于，数值计算得到的曲线关于正、负漂角是对称的，而试验数据的曲线则出现了不对称的形状。图3（b）中俯仰力矩试验值曲线的不对称性要比图5（a）中垂向力试验值曲线的不对称性更加明显。Roddy[5]的报告中没有说明产生这种不对称性的原因。在Watt[6]的试验结果中也出现了类似的不对称性，他认为这是由于前部的支架对流场的干涉，以及（或者）潜艇模型过于接近自由表面和水池底部造成的。

3.2 斜航和回转运动中的流场对比

图5显示了SUBOFF潜艇模型在两种典型操纵运动中受到的垂向受力沿着艇体纵向方向的分布：（1）水平面的斜航拖曳试验（β=3°）；（2）水平面的旋臂试验( )r' = 0.15 。这两张图中的明显区别在于：在斜航拖曳试验中，指挥台之后的艇体上受到的垂向力方向向下（Z'为正值）；而在旋臂试验中，艇体后段受到向上的垂向力（Z'为负值）。

图5 斜航试验和旋臂试验中艇体截面遭遇的垂向力系数Z'沿着船体纵向的分布曲线Fig.5 Longitudinal distribution of normal force coefficient Z'on the SUBOFF model at oblique towing test and rotating arm test

“离面载荷”的根源来自于指挥台围壳泄出的涡造成的不对称尾流。如果潜艇模型仅仅是一个回转体，那么在水平面斜航或回转过程中，由于几何对称，周围流场必然也是关于水平面对称的，自然也就不存在垂向力Z'和俯仰力矩M'。但是，对于真实潜艇来说，指挥台等附体的存在引入了几何上的不对称。特别是指挥台梢部泄出强烈的涡，对指挥台之后的艇体周围流场造成了显著的影响，艇体上下表面的速度、压力不对称，引起垂向力和力矩也就不难理解了。另外，由于斜航试验和旋臂试验中潜艇模型的流场特征存在差异，所以如图5（a）和5（b）所示的两种情况下艇体上受到的垂向力出现差异也并不令人意外。

为了理解“离面载荷”的产生机理，下面我们对两种试验中的潜艇流场进行对比：

（1）水平面斜航试验（β=3°）

图6显示的是在λ/L=0.34（λ是从船首向后的纵向距离）处横截面上的流场，这个平面是一个距离指挥台围壳尾端很近的横截面。在斜航试验中，当指挥台遭遇到斜向来流时，其工作状态类似一个展长较短的机翼，指挥台的迎风面和背风面之间存在压力差，这个压力差驱使着流体翻越指挥台顶盖从高压区流向低压区，发生流动卷曲；同时，在远方斜向来流的带动下，这个旋转卷曲的流体被拖曳着向下游传输，这样就形成了指挥台梢部的泄出涡。

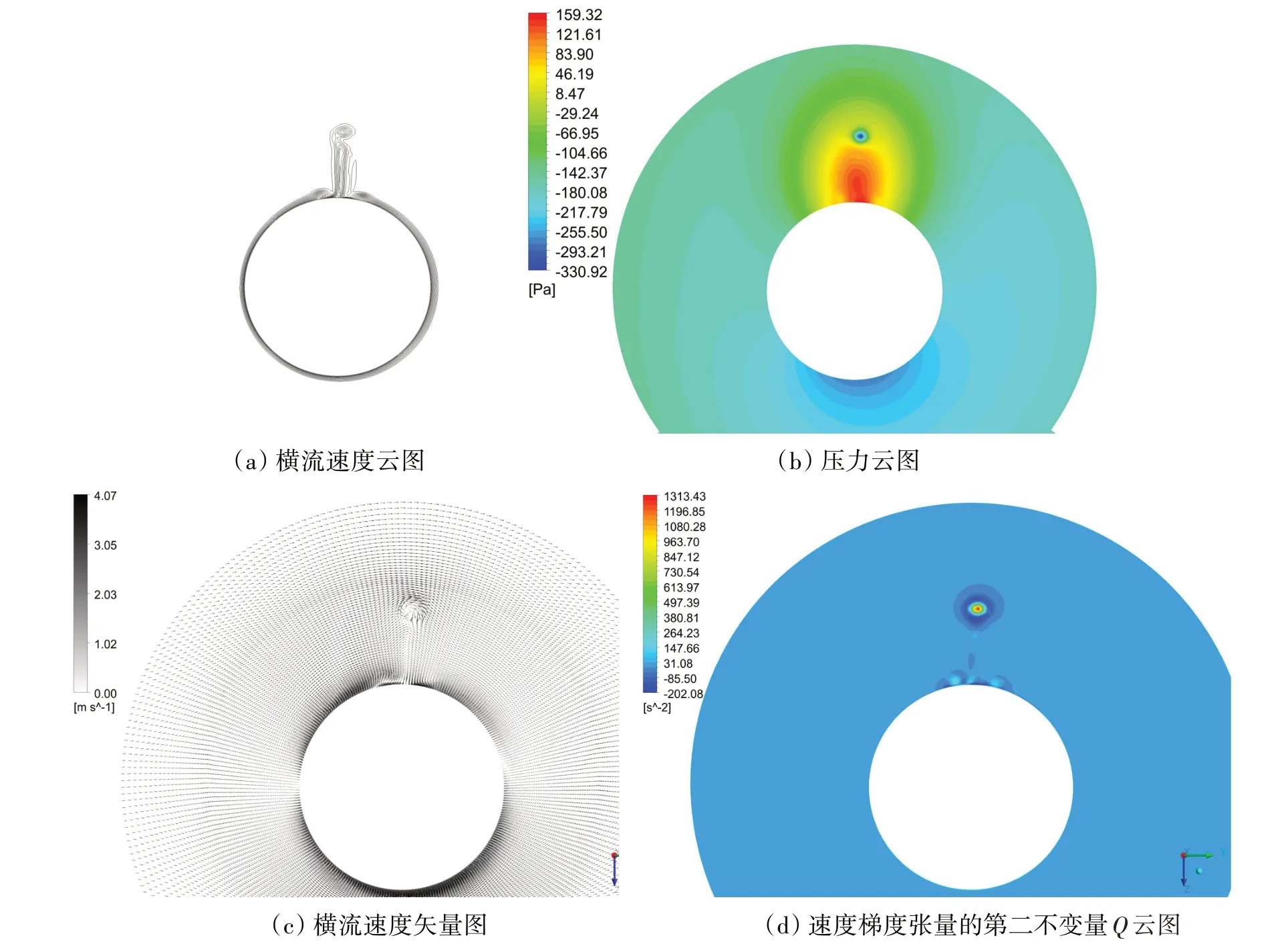
图6 斜航试验（β=3°）中SUBOFF潜艇模型的横截面λ/L=0.34上的流场Fig.6 Flow field at λ/L=0.34 for SUBOFF model at β=3°

从图6 可以很明显地观察到指挥台梢部泄出涡，另一个明显的流动现象是指挥台根部的两侧出现了一对马蹄涡。图7 显示的是在λ/L=0.6 时横截面上的流场，这个平面是一个典型的位于艇体后半段的横截面。由于艇体遭遇来自左舷的斜向来流，所以指挥台梢涡和马蹄涡都受到此影响，它们在这个λ/L=0.6截面上的位置相对于图6，都向右舷发生了偏移。

在图8 中，我们示意性地绘出了环量、横流和艇体遭受的垂向力之间的关系。Feldman[2]指出，从指挥台泄出的环量沿两个路径向下游传输，一个是指挥台梢涡，另一个是梢涡在潜艇艇体内诱导出的镜像涡。这个镜像涡（或称为诱导涡）附着在指挥台之后的艇体上，强度和指挥台梢涡成正比，但是旋转方向相反。

图7 斜航试验（β=3°）中SUBOFF潜艇模型的横截面λ/L=0.60上的流场Fig.7 Flow field at λ/L=0.60 for SUBOFF model at β=3°

在图6（c）和图7（c）中可以看到，围绕着指挥台梢涡的速度矢量沿顺时针方向旋转。因此在图8中，指挥台梢涡的环量是顺时针方向，而艇体的镜像涡的环量是逆时针方向。在此处，艇体左舷是迎风面，因此根据库塔-儒科夫斯基定理，船体镜像涡的环量与横向流动相互作用，在潜艇后部艇体上产生向下的垂向力。根据上述流动现象推断的受力方向和图5（a）中的垂向力Z'分布情况也一致。艇体后部受到向下的垂向力（+Z'）自然就会形成一个使潜艇抬首的力矩。

根据库塔-儒科夫斯基定理，Ẑ= -ρvΓ，也就是说艇体横截面的受力Ẑ与横流速度v和环量Γ之积成正比。我们知道，指挥台梢涡环量和指挥台遭遇的漂角β成正比；前面也提到，艇体镜像涡和指挥台梢涡的大小成正比[4]。也就是说，艇体镜像涡的环量Γ也和指挥台遭遇的漂角β成正比。此外，在斜航试验中，横向速度v和β（对于漂角β较小的情况，sinβ≈β）成正比。这样一来，根据Ẑ= -ρvΓ可知，在漂角不大的情况下，斜航试验中艇体横截面受到的垂向力就和β2（或sin2β）成正比，这就解释了图3中曲线呈现出抛物线形状的原因。

（2）水平面旋臂试验（r'=0.15）

在斜航试验中，潜艇模型各个横截面处的局部漂角都是相同的β角度。然而旋臂试验则不同，由图9可见，我们将潜艇原点O处的漂角设置为零，也就是说在原点O处潜艇的纵轴线与回转运动的线速度方向相切。在艇体首垂线处，局部的漂角是一个最大的负值；沿着艇体向后，局部漂角的绝对值逐渐减小，直到原点O处局部漂角成为零；再进一步向艇尾方向，局部漂角一直为正值，而且绝对值逐渐变大。

图8 斜航试验（β=3°）中SUBOFF潜艇模型的横截面λ/L=0.60上的环量和横流示意图Fig.8 Circulation schematic at λ/L=0.60 for SUBOFF model at β=3°

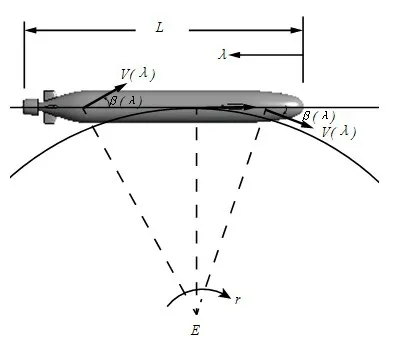
图9 旋臂试验中局部漂角沿着潜艇模型纵向位置而变化Fig.9 Drift angle variation with longitudinal location

图10 显示的是在λ/L=0.34 处横截面上的流场，和图6 类似，在此处可以很明显地观察到指挥台梢部泄出涡和指挥台根部两侧的一对马蹄涡。和图6 不同的是，由于指挥台位于艇体前半部分，如图9 所示，在这里右舷是迎风面，横流方向向左，因此从图10（a）中可见梢涡略向左舷偏移。另外，从图10（c）中也可以看到，梢涡周围的速度矢量沿逆时针方向旋转。图11 显示的是在λ/L=0.6 横截面上的流场，此处位于艇体后半部分，从指挥台泄出的梢涡传输到此截面，旋转方向没有改变，仍然是逆时针的。然而局部漂角改变了方向，从图9可见，在这里左舷是迎风面，此处的局部横流方向向右。与图10相比，梢涡和马蹄涡向左舷偏移的程度变小，如果在更靠近艇尾的横截面上，梢涡和马蹄涡会向右舷偏移。

图10 旋臂试验（r'=0.15）中SUBOFF潜艇模型的横截面λ/L=0.34上的流场Fig.10 Flow field at λ/L=0.34 for SUBOFF model at r'=0.15

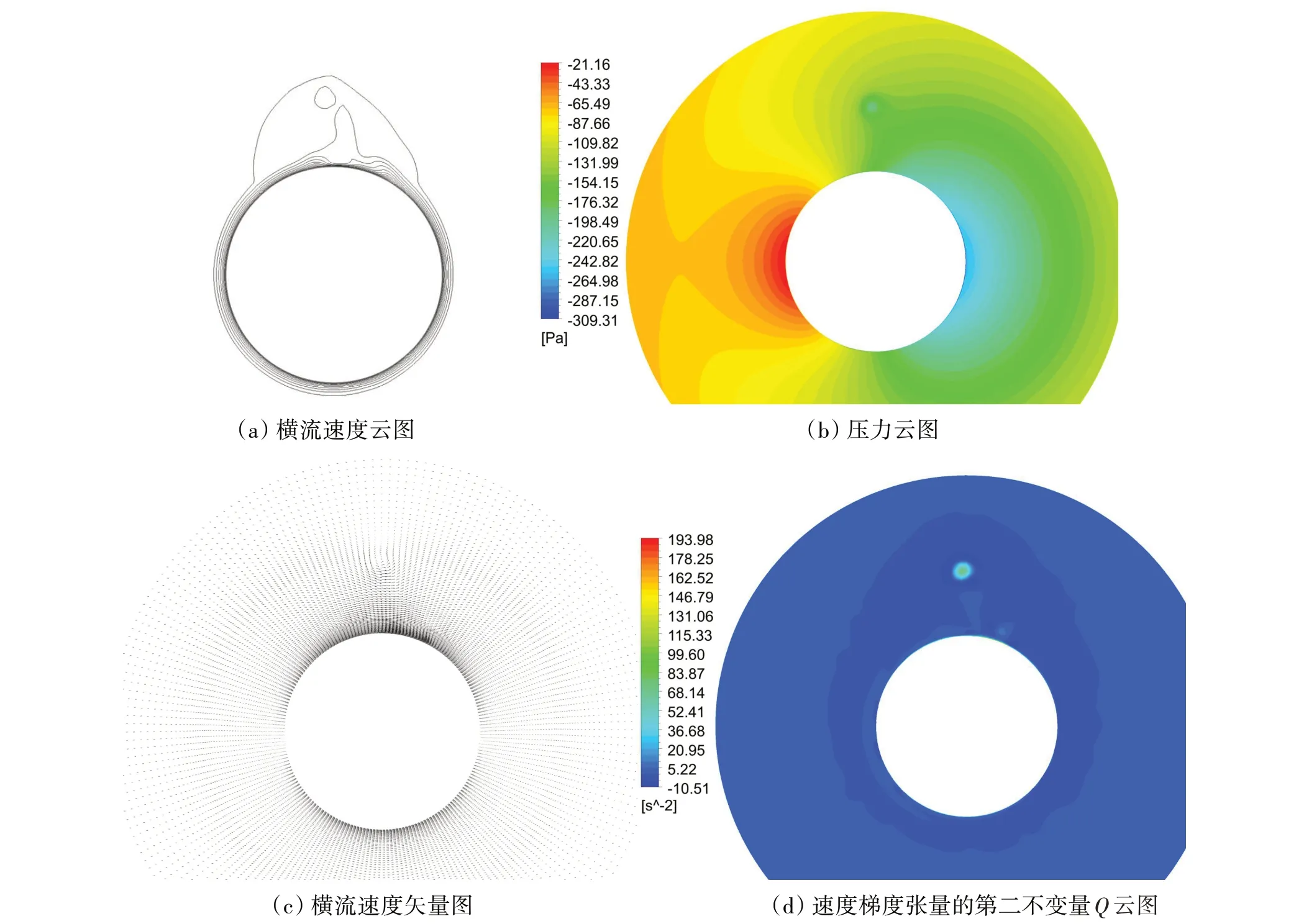
图11 旋臂试验（r'=0.15）中SUBOFF潜艇模型的横截面λ/L=0.60上的流场Fig.11 Flow field at λ/L=0.60 for SUBOFF model at r'=0.15

如图12 所示，在λ/L=0.6 的横截面上，艇体镜像涡的环量为顺时针，此处艇体遭遇左舷来流，所以根据库塔-儒科夫斯基定理，可以推断出此处艇体截面将遭遇方向向上的垂向力。这一推断和图5（b）中λ/L=0.6 处垂向力Z'数值为负也一致。

4 结 论

图12 旋臂试验（r'=0.15）中SUBOFF潜艇模型的横截面λ/L=0.60上的环量和横流示意图Fig.12 Flow field at λ/L=0.6 for SUBOFF model at r'=0.15

本文用基于求解RANS 方程的数值方法对潜艇水平面运动中受到的“离面载荷”进行了预报，成功获得了SUBOFF潜艇模型在斜航拖曳试验和旋臂试验中遭遇的“离面”垂向力和俯仰力矩。在漂角不大的情况下，计算得到斜航拖曳试验中潜艇模型遭受的“离面载荷”与漂角的平方成正比，这一趋势和试验测量的结果吻合得很好。

“离面载荷”来源于指挥台梢涡诱导的环量与指挥台之后艇体上的横流之间的相互作用。不同运动状态下艇体绕流细节的差异也将对“离面”受力和力矩产生显著的影响，因此正确捕捉艇体周围的涡流细节是正确预报“离面载荷”的必要条件。

对于进行水平面斜航试验的潜艇模型来说，涡流场的相互作用最终导致艇体后段遭遇向下的垂向力和抬首力矩。对于进行水平面旋臂试验的潜艇模型来说，不同的纵向位置对应着不同的局部漂角，这样一来，从船首到船尾，横向流动的速度方向就会发生逆转，而涡流场的相互作用最终导致艇体后段遭遇向上的垂向力和埋首力矩（至少对于大多数旋转速度来说）。

遗憾的是，目前没有在公开文献中看到关于SUBOFF 潜艇模型在旋臂试验中遭受“离面载荷”的试验数据，还无法对计算结果进行验证。因此，将来有必要开展高质量的潜艇回转试验，以便于CFD预报的验证。