基于偏微分方程的定向插值在偏移成像中的应用
韩复兴, 孙章庆, 陈祥忠, 高正辉, 王瑞兴, 刘俊成, 王丽丽
1 吉林大学地球探测科学与技术学院, 长春 1300262 北京桔灯地球物理勘探股份有限公司, 北京 1022003 吉林油田地球物理勘探研究院, 松原 138006
0 引言
基于弹性波传播方程高频近似的射线理论类偏移成像技术(Hill, 1990, 2001; 高成等, 2015; Gao et al., 2017;韩建光等,2017),其在实现偏移成像的过程当中,采用射线理论方法求解运动学和动力学射线追踪系统获得波场传播所需的走时振幅和相位信息,然后进行地震波场的延拓外推从而达到最终成像的目的.其实现过程和实现方式相对于波动方程类偏移成像具有很大的时效性和经济性,因此一直是工业界应用的主流成像方法和技术(岳玉波, 2011;杨珊珊等,2015;袁茂林等,2016).基于体波、面波等地震弹性波和电磁波的有效联合,解译了华南深部结构(Di et al., 2021).那么在应用射线理论实现波场延拓成像的过程当中,难免会遇到依赖速度模型进行的射线追踪系统的求解.在实际应用过程当中,一般给定的速度模型都比较复杂,而且是以离散的形式只给定网格节点上的数值,非网格节点上的值只能通过构建的插值算法来进行插值计算.在应用射线理论进行运动学和动力学追踪计算中,波场随着时间的不断外推增加,每一步计算所应用到的速度场信息不一定都落在给定的原离散网格上,如果计算所需要的速度场不在给定的离散节点之上,就需要对速度模型进行插值计算,从而解决在波前外推当中速度在x、z方向上非网格节点处的插值问题.众所周知,插值算法以及应用插值算法所得的插值计算结果的准确性直接影响着速度模型上计算的走时、相位和振幅,最终影响到偏移成像的质量(韩复兴, 2009).在偏移成像的过程当中,给定的速度模型往往都具有一定的速度梯度,如何根据速度梯度的空间变化选择一种高效、稳定的插值算法对于实现基于高频近似理论的射线类偏移成像有着十分重要的作用(Gao et al., 2017).
截止到目前为止,在数值计算当中常用的插值算法主要分为两大类型:第一大类型主要为通过给定的网格节点上的数值直接进行插值计算,例如双线性插值、分片线性插值、临近域插值、距离加权插值等.直接计算这种类型的插值算法经过几十年的发展和完善,算法相对成熟和稳定,而且简单实用、计算速度快.在实际插值计算处理当中,该类插值算法只需要4个已知网格节点上的属性值进行插值计算,但缺点在于只能达到二阶近似的计算精度,确保了计算的效率而忽略了计算的精度问题;第二大类型主要为基于构建插值核函数的插值计算方法,例如卷积类插值(韩复兴等, 2008a,b)、样条插值、双立方厄米特插值(王德人和杨忠华, 1990; Keys, 1981)、双三次多项式插值等等,该类插值算法依据所构建的核函数不同,所选取插值点周围的网格节点数也不尽相同,二维三次卷积、双三次多项式插值等需要插值点周围的16个网格节点上的属性值进行插值,二维四次卷积依据其核函数需要插值点周围的36个网格节点上的属性值进行插值.由于采用的网格节点数比较多,该类核函数插值算法计算精确度相对比较高,并且根据实际需求可以满足插值结果在网格点处的一阶导数、二阶导数连续,在实现的过程当中考虑算法的优化能够同时保证计算具有较高的计算效率.但该类算法存在的问题在于由于插值过程当中应用的插值点周围的网格节点数较多,虽然保证了插值结果的计算精度和导数的连续性,但对于速度梯度在空间上变化剧烈的模型来说,忽略了原始速度模型横向、纵向空间结构的变化,从而造成插值结果后的速度模型不满足原始速度模型空间梯度的连续性.也就是说基于插值核函数的插值算法的缺点在于其插值函数一旦固定下来对于整个模型空间来说就是不变的,这种不变性对于速度梯度变化不明显的模型来说是可以适应的,但对于速度梯度在横向和纵向变化较大的模型来说,这个固定核函数的插值算法就很难适应.如果应用基于固定核函数的插值算法在速度梯度变化剧烈的模型上进行插值计算就会造成梯度变化大的地方边缘模糊和锯齿现象,最终造成射线路径、走时和振幅相位的误差,影响偏移成像的结果.
为了解决上述射线类偏移成像求解射线追踪系统当中遇到的速度在波场延拓过程当中的不连续问题,本研究的主要内容就是考虑原始速度模型的空间结构,基于变分原理引入基于速度梯度构建的偏微分方程插值算法,使模型空间被插值点处速度梯度的空间变化尽可能与原始模型保持一致(Perona and Malik, 1990; Catté et al., 1992; Alvarez et al., 1992; Jiang and Moloney, 2002a,b),从而实现基于原始速度模型空间梯度变化的插值计算.由于偏微分方程方法本身所固有的特性(局部特征不变性、解的唯一性和线性叠加性),自偏微分方程算法提出以来,随着时间的推移,目前已经应用到各个领域(Perona and Malik, 1990; Catté et al., 1992; Alvarez et al., 1992; 仵冀颖, 2009; 肖义男, 2005).因此,在射线类偏移成像当中应用基于速度梯度构建的偏微分方程插值算法可以最终实现不破坏原始速度模型空间结构前提下的插值计算,从而获得较为准确的走时、振幅和相位信息,最终提高偏移成像的质量.
1 偏微分方程(Partial Differential Equation)的插值算法
基于速度梯度构建的偏微分方程插值算法在进行插值计算的过程当中引入总变分最小原则,使被插值点的速度值v(x,z)满足(Jiang and Moloney, 2002a,b):
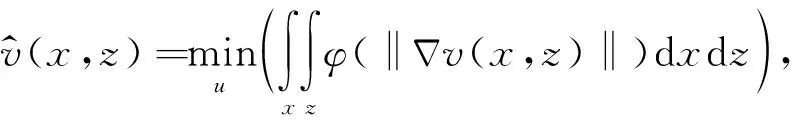
(1)
也就是要求需要插值地方的速度的梯度尽可能与原始速度模型的空间结构保持一致,从而达到对原始速度模型空间结构的保护性.其约束条件为采用基于速度梯度构建的偏微分方程在网格节点上所得的插值计算结果必须等于原始速度模型网格节点上的速度值,即:
(2)
其中v(i,j)是原始速度模型空间网格节点上的速度值,X和Z是原始速度模两个方向上的空间尺度,Δh、Δk是X方向和Z方向上的空间采样间隔,φ(·)≥0是一个递减函数.
对于公式(1)来说,初始条件的选择直接决定着该问题的求解难易程度.为了使公式(1)的求解简单化,引入对被插值点速度方向角的条件限制(Jiang and Moloney, 2002a,b):

(3)
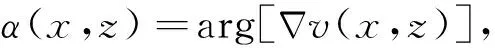
假设已知原始速度模型网格节点处的梯度角,且在应用基于速度梯度构建的偏微分方程插值计算过程当中原已知的梯度角不随插值条件发生改变,即限定条件为:
(4)
(5)
在实际插值计算当中梯度角α(x,z)可以采用数值计算的方法获得.
基于以上假设,在偏微分方程插值计算的过程当中,首先需要求解梯度角α(x,z),即(3)式,接下来求解基于约束条件(2)和约束条件(4)的变分问题,即可解决基于变分原理的插值计算问题.
关于插值点处梯度角的计算问题如下,对应(5)式的Euler方程为:
(6)
由于在实际计算过程当中只使用插值点4个斜线方向上的相邻速度值,所以(6)式可以简化为:
(7)
其中k∈{(i,j),(i,j+1),(i+1,j),(i+1,j+1)},αk表示对应于第k个速度点上的梯度角,因此得到非线性方程(7)的解为:
(8)
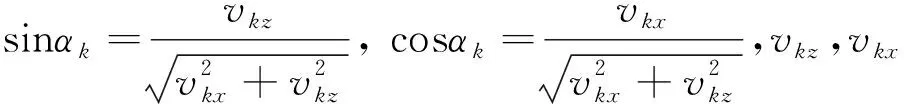
(9)
将公式(9)展开并代入方向角限定条件化简得到:
(10)
公式(10)是关于插值点处的梯度角以及插值点处速度偏导数的计算公式,将该公式采用数值计算的方法进行离散处理,然后应用被插值点周围的4个已知点上的速度值就可以进行插值计算求得被插值点处的速度值.其具体的计算步骤如图1所示.
图1中G(x,z)为需要插值的点,h为速度模型X方向上的网格间距,k为速度模型Z方向上的网格间距,v(i,j)、v(i+1,j)、v(i,j+1)、v(i+1,j+1)为已知网格节点上的速度值,A1、A2、B1、B2为计算过程当中的待求点,偏微分方程插值计算步骤如下:
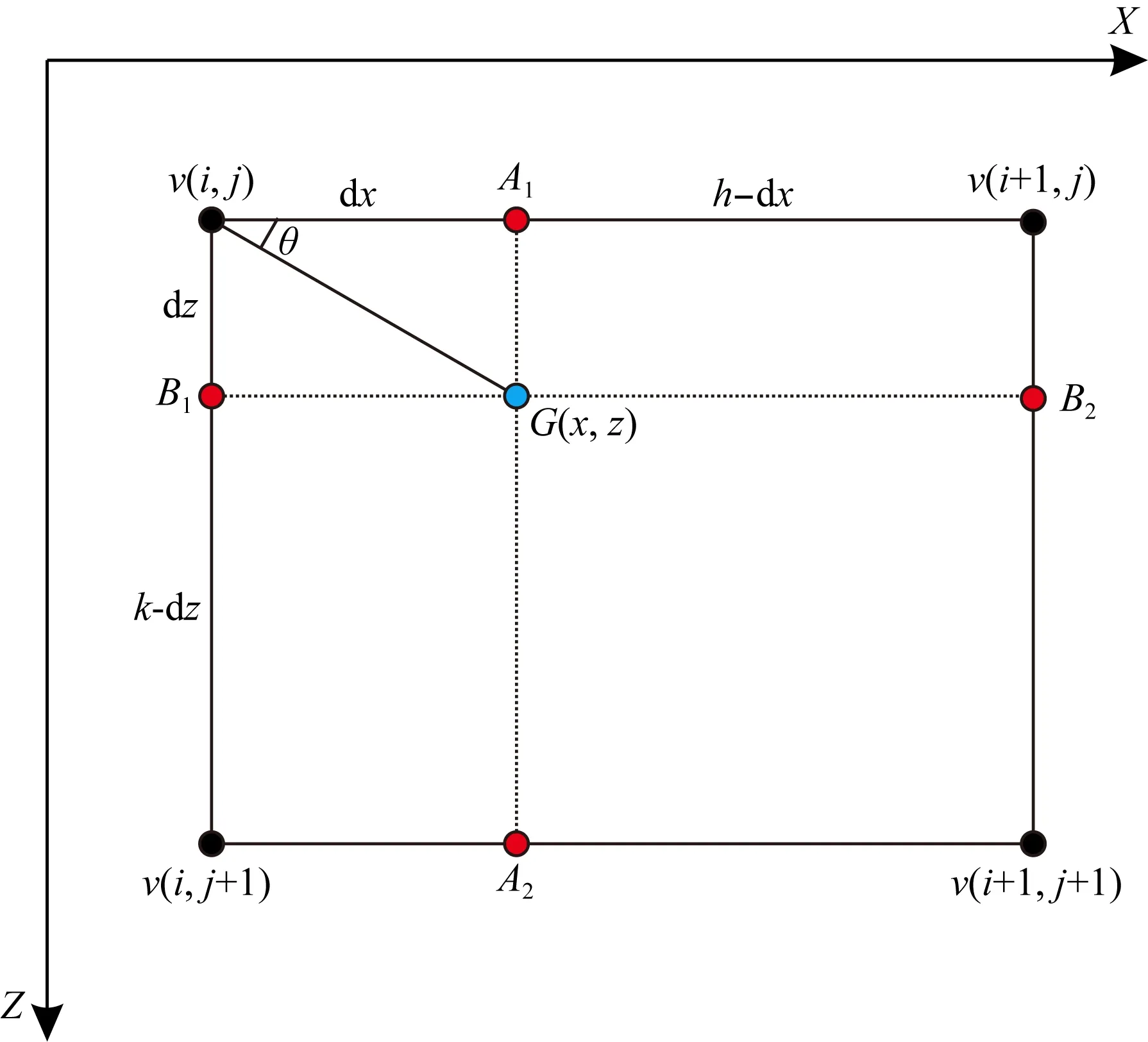
图1 基于速度梯度的偏微分方程插值示意图Fig.1 Schematic diagram of partial differential equations interpolation
(1)首先应用四个已知网格节点上的速度值v(i,j)、v(i+1,j)、v(i,j+1)、v(i+1,j+1)求解待定点A1、A2、B1、B2,即:
(11)
(2)然后应用不等距差分和泰勒级数展公式求解被插值点处的速度导数值vxx(x,z)、vxz(x,z)、vzz(x,z),即:
(12)
(3)把通过第二步解出的值vxx(x,z)、vxz(x,z)、vzz(x,z)、vzx(x,z)带入公式(10),就可以获得待求点处的速度值G(x,z),其公式为:
(13)
其中:
(14)
2 插值试算
下面以地震数据处理当中常用的Marmousi速度模型和Sigsbee速度模型为例,分析说明在原始速度模型上进行插值计算后速度模型空间结构特别是模型边缘位置的变化情况.Marmousi速度模型横向384个网格节点,纵向122个网格节点,原模型横向和纵向的网格间距Δx=Δz=24 m,现在采用dΔx=dΔz=4 m的间距进行插值计算,插值后速度模型横向网格点数为2298,纵向网格点数为726,在相同的运算环境下,采用卷积类插值算法插值计算耗时18.899 s,采用偏微分方程插值计算耗时16.204 s,原Marmousi模型和经过卷积插值、PDE插值计算后的结果如图2所示.为了进一步分析说明不同插值算法对速度模型空间结构和速度梯度变化区域边缘的影响,将原模型和插值计算后模型红色局部区域进行放大,如图3所示.通过图3可以看出,采用固定核函数的卷积类插值算法在原始速度模型空间结构梯度变化剧烈的区域,由于采用的插值点数较多(16个),插值造成的结果就是破坏了原模型的空间梯度结构,因此造成插值后速度模型红色部分同原始速度相比,在边缘区域变得模糊,而基于速度梯度构建的偏微分方程插值算法,由于去插值函数的单调性和可变性,插值结果基本保持和原始速度模型空间结构的一致性.
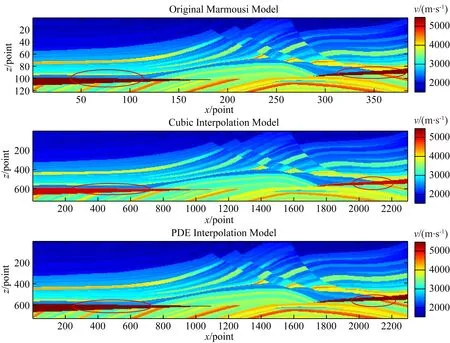
图2 Marmousi速度模型以及应用不同插值算法插值后的速度模型Fig.2 Original Marmousi velocity model and its interpolation results using cubic and PDE algorithms
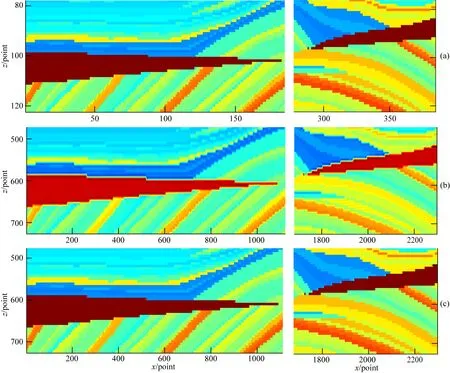
图3 (a) 原速度模型局部区域放大; (b) 卷积插值后局部区域放大; (c) 偏微分方程插值后区域局部放大Fig.3 (a) Partially enlarged area of original Marmousi model; (b) Partially enlarged red area of interpolated Marmousi model used cubic; (c) Partially enlarged red area of interpolated Marmousi model used PDE
Sigsbee速度模型横向2400个网格节点,纵向800个网格节点,横向网格间距Δx=37.5 m,纵向网格间距为Δz=25 m.采用x方向间距为dΔx=12.5 m,z方向间距为dΔz=5 m进行插值计算,插值后速度模型横向网格点数为7197,纵向网格点数为3995,在相同的运算环境下,采用卷积类插值算法完成计算耗时408.972 s,采用基于速度梯度的偏微分方程插值完成计算耗时374.696 s.原模型以及插值计算后所得到的速度模型如图4所示.通过对比插值前后的速度模型可以看出,对于速度梯度变化比较剧烈的区域,同样由于卷积类插值算法采用的插值点数较多,忽略了原模型梯度的空间变化,插值计算后整个模型的边缘区域变得模糊,而采用基于速度梯度的偏微分方程插值后的速度模型考虑和原模型速度梯度的空间变化,边缘区域都得到的较好的保持.
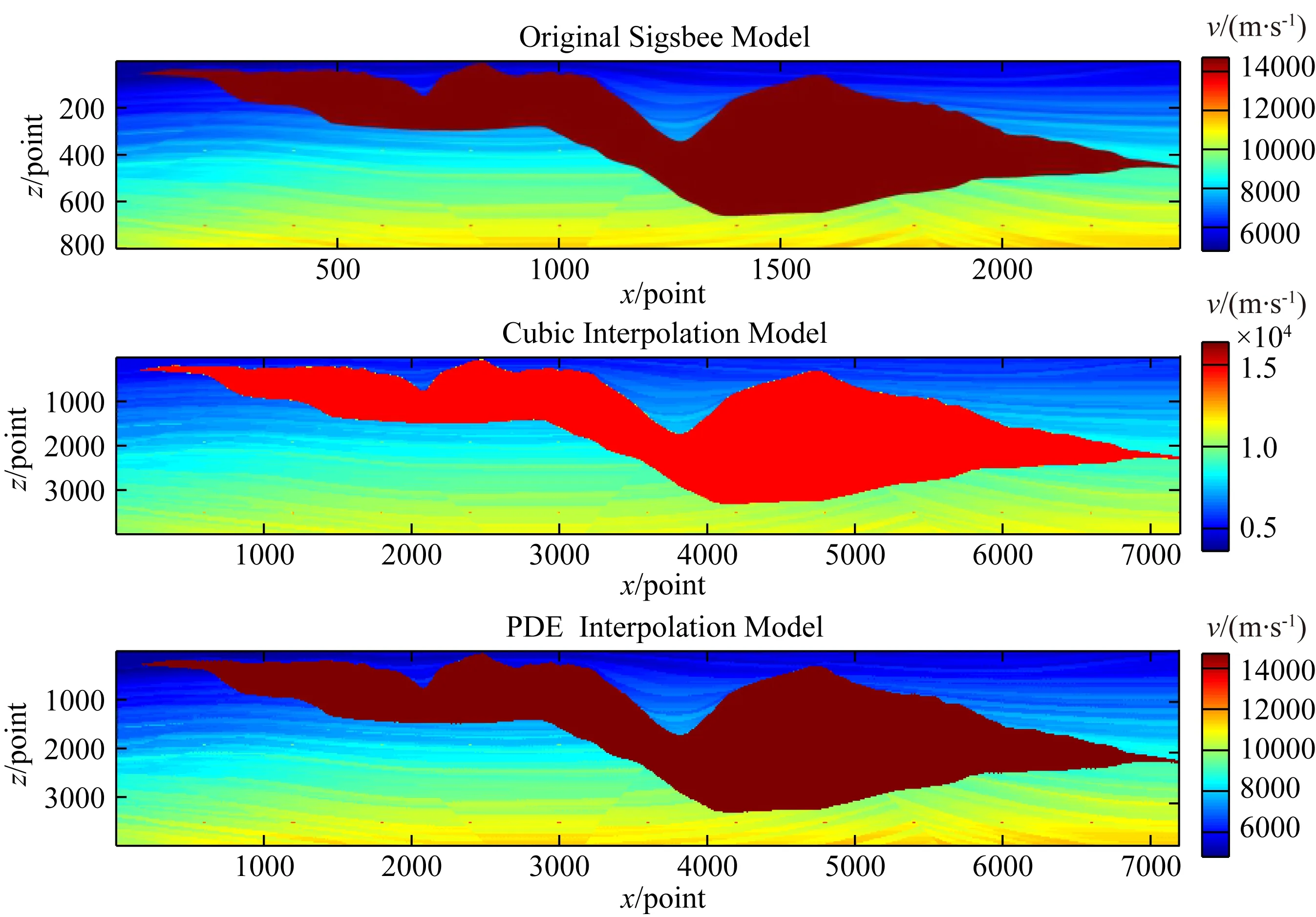
图4 Sigsbee模型以及应用不同插值算法插值后的模型Fig.4 Original Sigsbee velocity model and its interpolation results using cubic and PDE algorithms
另外,通过插值前后的模型对比也可以看出,在速度模型底部红色圆点区域,基于速度梯度的偏微分方程插值能够较好的保持原始速度的局部特征,红色圆点清晰可见,而卷积类插值后红色圆点区域变得模糊.其主要是因为Sigsbee盐丘模型内外速度差异比较大,速度梯度在局部变化特别明显,卷积类插值核函数的空间不变性造成了其难以适应速度梯度变化剧烈区域的插值计算,从而造成对原模型空间结构的改变.
3 射线路径计算
为了进一步说明偏微分方程插值的优越性,下面给出一些实际的速度模型,分别用卷积类插值和PDE插值计算射线路径并分析其差异.
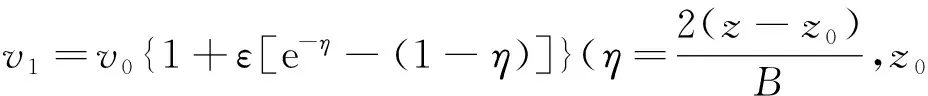
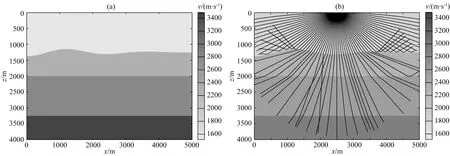
图5 (a) 海底起伏速度模型图; (b) 射线路径示意图,黑色实线为二维三次卷积插值射线路径,虚线为偏微分方程插值射线路径Fig.5 (a) Velocity model of seafloor relief; (b) Sketch of ray paths. The solid black line is from two-dimensional cubic convolution interpolation, and dotted line is from PDE interpolation
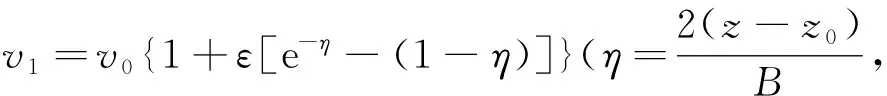
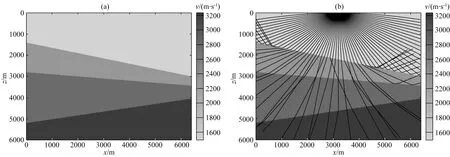
图6 (a) 倾斜海底层速度模型; (b) 射线路径示意图,黑色实线为二维三次卷积插值射线路径,虚线为偏微分方程插值射线路径Fig.6 (a) Velocity model of inclined seafloor layer; (b) Sketch of ray paths. The solid black line is from cubic convolution interpolation, and the dotted line is from PDE interpolation
速度模型3:Marmousi速度模型:模型横向网格点数为384,纵向网格节点数为122,横向纵向网格间距都为24 m,射线路径计算时间步长为0.004 s,应用二维三次卷积插值以及PDE插值计算的射线路径如图7所示.
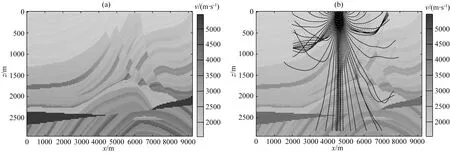
图7 (a) Marmousi速度模型图; (b) 射线路径示意图,黑色实线为二维三次卷积插值射线路径,虚线为偏微分方程插值射线路径Fig.7 (a) Marmousi velocity model; (b) Sketch of ray paths. The solid black line is form two-dimensional cubic convolution interpolation, and the dotted line is from PDE interpolation
从图5—图7的射线路径计算结果可以看出:对于起伏海底以及倾斜层速度模型,由于每一层层速度都为常数,插值计算只发生在层与层之间,由于不同插值算法应用的插值点数以及对边界的处理不同,应用二维三次卷积插值以及PDE插值得到的射线路径会在在第一个分界面后存在差异;而对于速度横向纵向剧烈变化的Marmousi 速度模型来说,由于其速度模型横向纵向梯度变化十分明显,因此插值点速度由于采用的插值算法不同而造成图7b中射线路径的差异.
4 偏移成像结果对比
下面以南海复杂的崎岖海底大陡坡速度模型为例,验证在射线类偏移成像中插值算法的选取对成像结果的影响.复杂的大陡坡模型横向网格点数为3001,纵向网格点数为1501,横向和纵向网格间距都为2.5 m,如图8a所示.数值模拟采用炮间距500 m,共16炮,每炮601道,道间距12.5 m,时间采样间隔2 ms.分别采用卷积类插值算法和偏微分方程插值算计算射线路径和走时并应用高斯波束实现最终的偏移成像,偏移结果剖面如图8b、c所示.
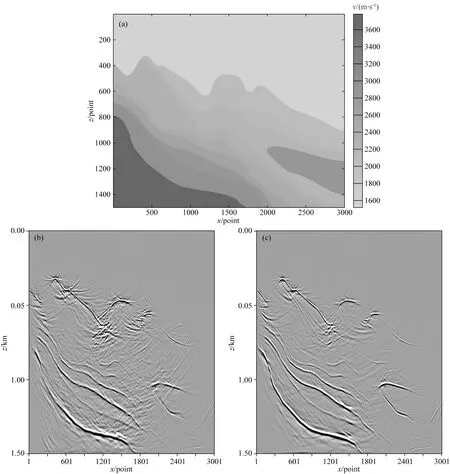
图8 (a) 复杂的大陡坡速度模型; (b) 卷积类插值光滑处理30次后大陡坡速度模型偏移结果; (c) PDE插值光滑处理30次后大陡坡速度模型偏移结果Fig.8 (a) Velocity model of big complex steep slope; (b) Migration results of the velocity model after smoothing with two-dimensional cubic convolution interpolation; (c) Migration results of the velocity model after smoothing with PDE interpolation
从图8的偏移成像剖面结果可以看出,对于复杂的南海某区域速度梯度变化较大的大陡坡速度模型,在射线类偏移成像当中采用基于速度梯度构建的偏微分方程插值算法对原始速度模型进行插值处理后获得成像结果其海水底部层位清晰可见,所获得成像效果要明显优于采用二维三次卷积插值所获得的偏移成像效果.
5 结论
本文针对基于弹性波传播方程高频近似的射线理论类偏移成像过程当中求解运动学和动力学追踪系统当中所遇到的模型非网格节点处速度以及导数的插值问题,基于原始速度模型空间梯度变化,引入总变分最小原则,使插值点处的速度沿x方向和z方向的梯度与原始模型梯度保持一致的要求构建偏微分方程插值算子实现非网格节点处速度以及速度导数的插值计算.通过在两个速度模型上的插值对比分析可以得出,由于偏微分方具有很好的局部特征保持特性,应用基于速度梯度构建的偏微分方程插值算法对速度模型进行插值可以较好的保持原速度模型的空间结构和边缘特征,同时通过插值的耗时可以看出,偏微分方程插值速度要快于卷积类插值;通过不同模型的射线路径计算可以得出,由于不同的插值算法采用的插值点不同以及对速度模型的边缘处理不同,偏微分方程插值能更好的保持原始速度模型的空间结构,从而造成相同模型射线路径存在较大的差异.通过图8南海复杂的大陡坡模型的成像结果也能够很好的说明应用基于速度梯度构建的偏微分方程插值算法对原始速度模型进行插值计算能够在保持原始速度模型空间结构的同时可以获得较好的成像结果.

