基于吸收边界条件的瞬变电磁法三维矢量有限元快速正演
张永超, 王光杰, 李宏杰, 廉玉广, 李文,邱浩, 牟义
1 煤炭科学技术研究院有限公司安全分院, 北京 100013 2 煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院), 北京 100013 3 北京市煤矿安全工程技术研究中心, 北京 100013 4 中国科学院大学, 北京 100049 5 中国科学院地质与地球物理研究所 页岩气与地质工程重点实验室, 北京 100029
0 引言
瞬变电磁法又称时间域电磁法,是近年来发展迅速的一种地球物理勘探方法.它具有可在近区测量、旁侧效应影响小、对低阻体敏感等优点(朴化荣,1990),被广泛地应用于水文地质调查、金属矿勘探、工程勘查等领域.目前,实际工作中瞬变电磁法的反演解释仍以一维方法为主(薛国强等,2008),分辨率较低,在某些地质条件复杂的地区难以取得理想效果.Di等(2021)耦合弹性波和电磁波数据,解译了华南陆块深部-浅部的地质结构.为更好地指导瞬变电磁法的资料处理、反演解释、进一步改善勘探效果,开发速度快、精度高、对复杂地电模型适用性好的三维正演技术已成必由之路.
目前常用的三维数值模拟方法主要有:积分方程法(Sanfilipo and Hohmann,1985;Zhdanov et al.,2006)、有限差分法(Wang and Hohmann,1993;Commer and Newman,2004;孙怀凤,2018,2021)和有限元法(殷长春等,1994, 2013;李瑞雪等,2016a, 2016b;余翔等,2017;周建美等,2018;Zeng et al., 2019),其中有限元法具有对复杂地质模型的适用性强、形成的总体系数矩阵是稀疏且对称、易于并行等优点,成为电磁法领域解决正演问题应用最为广泛的方法(Jin,2014).Kuo和Cho(1980)利用有限元法对低阻覆盖层下的低阻矿体的瞬变电磁法响应进行了三维数值模拟,得到的曲线形状和数量级与野外实测数据基本一致,证明了该方法的可行性.此后,Pridmore等(1981)也对有限元求解三维瞬变电磁法正演问题进行了探索性研究.Sugeng(1998)采用异常场和背景场分离的思路,使用六面体矢量单元对回线源瞬变电磁法进行了三维正演.Jin等(1999)基于兰乔斯谱分解法(SLDM),分别运用节点有限元法和矢量有限元法对时间域和频率域的三维电磁场进行了数值模拟.Ralph-Uwe等(2008)提出了一种快速的基于频域有限元法离散、Krylov子空间投影技术建立的模型简化方法求得频域响应,然后通过余弦变换求得时间域电磁场响应.Um等(2010)提出了用于电性源瞬变电磁法的时域矢量有限元三维正演算法,其模型剖分采用四面体网格,时间离散使用隐式后退欧拉法,边界条件选用Dirichlet齐次边界条件,模拟了海洋时间域电磁场.李建慧(2011,2013),刘亚军(2019)利用矢量有限元法对大回线源瞬变电磁法进行了三维正演,其算法从电场双旋度方程出发,模型剖分采用六面体单元,边界条件为电磁场切向分量为零的齐次边界条件,先通过异常场/背景场法求得频域响应,然后通过Gaver-Stehfest变换得到时间域响应.张博等(2016)采用矢量有限元法对带有起伏地形的三维航空瞬变电磁法进行了数值模拟,其思路与李建慧的基本相同,不同之处在于为了更好地模拟地形起伏采用了非结构化的Delaunay四面体进行网格剖分,时频变换则采用余弦变换进行.李贺(2016)也基于时间域电场双旋度方程和电磁场切向分量为零的齐次边界条件,对典型地电模型的瞬变电磁法响应进了三维正演,模型剖分采用六面体矢量单元,时间离散则采用向后差分方式.李建慧(2017)基于齐次边界条件,采用将回线源视为多个电偶源的策略和非结构化四面体矢量单元正演了复杂形态回线源激发的瞬变电磁场分布.
综上所述,针对瞬变电磁法的三维有限元正演,目前常采用齐次边界条件作为模型的截断边界条件,这虽然简化了有限元弱形式方程的推导和后续的单元分析,但为了满足该条件,需要构建较大尺寸的模型,否则会产生由边界引起的非物理反射,降低正演结果的精度.而较大尺寸的模型意味着更多的网格单元,这会降低正演问题的求解速度.吸收边界条件能使边界的非物理反射最小化,因此可以缩小模型的尺寸、减少单元数目、加快求速解速度,或者在模型大小相同时提高正演结果的精度(Jin,2014).鉴于此,本文在前人研究的基础上引入吸收边界条件,以加快瞬变电磁法三维有限元正演的求解速度.
1 基于吸收边界条件的时间域矢量有限元法
1.1 矢量势控制方程推导
考虑场源的情况下,时间域中微分形式的麦克斯韦方程组如下
(1)
(2)
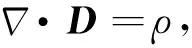
(3)
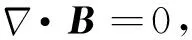
(4)
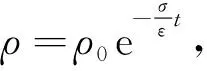
此外,还有三个辅助的介质特性方程如下
B=μH,D=εE,J=σE,
(5)
式中μ、ε、σ分别为磁导率、介电常数和电导率.针对地学问题,常见矿物的磁导率与真空磁导率十分接近,故μ=μ0.
由(2)、(4)式可假设
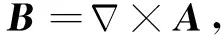
(6)
(7)
式中,A称为矢量势,φ称为标量势.
根据(3)、(5)和(7)式可得

(8)
将(6)、(8)式和介质特性方程代入(1)式,可得
(9)
1.2 吸收边界条件的选择
与频率域电磁法相比,瞬变电磁法的吸收边界条件较为困难.针对这一难题,本文的解决思路为:对于瞬变电磁法,由模型边界引起的非物理反射主要影响晚期数据,而晚期数据的频段集中在低频,针对这一特性,借鉴频率域吸收边界条件的思想,构建对低频吸收效果好的时间域吸收边界条件.
由于模型规模远大于发射线圈尺寸,外表面处的电磁波可以近似为以发射线圈为中心的球面波.借鉴Webb和Kanellopoulos(1989)的研究成果,采用形如下式的对球面波吸收较好的一阶吸收边界条件来减小模型规模,提升正演速度.
(10)
式中n为模型外表面的单位法向量,r为发射线圈中心点到外表面上任意一点的距离,ε′=(ε+|ε*|)/2,ε*=ε-iσ/2πf,为复介电常数,与介电常数、电导率和指定的主吸收频率f相关,f可以在n~n×10 Hz中选取.
1.3 弱形式推导
根据Galerkin加权余量法,结合矢量恒等式和散度定律,基于(9)式控制方程和(10)式边界条件的电磁场问题的弱形式方程为

(11)
式中,N为矢量基函数,Ω为模型区域,Γ为其外表面.
1.4 单元分析
矢量单元(又称棱边单元)很好地解决了节点单元由于未强加散度条件或强加法向连续性边界条件造成的“伪解”问题以及与结构相关的(如导体或介质的边缘或锐角)奇异性问题(Jin,2014),因此本文采用非结构化的一阶四面体矢量单元进行单元分析,相比六面体单元不仅能更好地模拟地形起伏或倾斜界面等复杂地电模型,还能在场源和异常体附近细分网格,提高结果精度.一阶四面体矢量单元的节点与棱边间的编码规则见图1.

图1 四面体矢量单元的节点和棱边示意图Fig.1 Sketch map of nodes and edges in a tetrahedral vector unit
单元e中,点(x,y,z)处的矢量势A在某一时刻t的值可由六条棱边的矢量基函数表示为(Jin,2014)
(12)
式中,上标e表示棱边i等编码均为基于单元的局部编码.其中矢量基函数
i=1,2,3,4,5,6
(13)

矢量基函数具有如下性质:
①散度为零,即
(14)
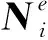
将(13)式代入(11)式,即可对弱形式方程进行空间离散.首先对(11)式左端体积分的第一部分进行离散,可得
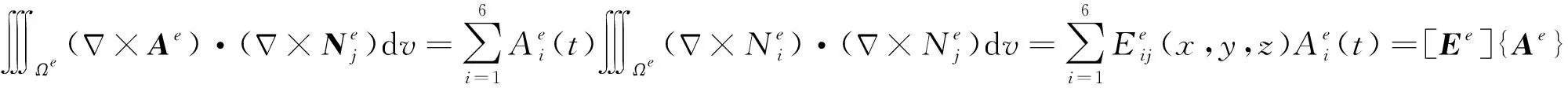
i,j=1,2,3,4,5,6
(15)
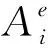

若单元e位于外表面Γ上则需要进一步计算(11)式左端的面积分部分:
(16)

对于(11)式的右端的计算,由于线电流的奇异性需将回线源看做多个较短导线元的组合,并在源附近采用较密的网格剖分.Ansari和Farquharson(2014)、李建慧等(2016)、李建慧等(2017)以该方法处理接地长导线源,取得了很好的效果.下面以图2中的Ⅰ边为例,详述发射电流加载过程.
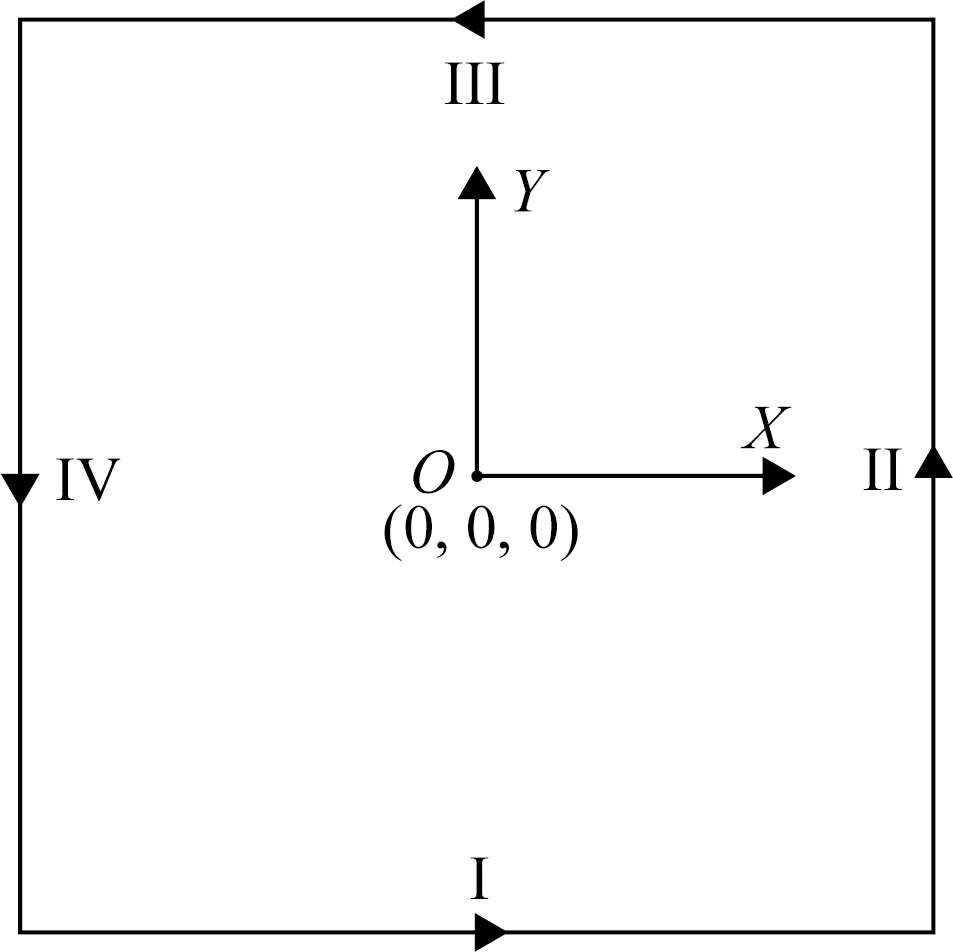
图2 发射回线示意图Fig.2 Sketch map of transmitter loop
设发射源位于z=0的平面上,四边中通过的电流方向如图2所示.网格剖分后,设Ⅰ边分布于若干个单元中,且总是与这些单元的某一个棱边重合,其源电流密度为
(17)
式中,I(t)为随时间变化的电流,指定不同的I(t)即可实现不同发射电流波形的加载,δ为冲激函数(又称狄拉克函数),dl为导线元的长度,(0,0,0)为
其中心坐标,ex表示x方向的单位矢量.
令{Qe}为6×1的列向量,其元素为
(18)
(19)
令[Re]=[Ee]+[Ke]、[Pe]=[Fe]+[Me],将上述单元矩阵后组装起来后,最终得到形如下式的总体矩阵方程:
(20)
1.5 时间离散
(20)式中未知数A(t)的求解可采用时间逐步积分法,它包括以中心差分法为代表的时间步长受算法稳定性限制的显式算法和以Newmark法为代表的时间步长只受精度限制的隐式算法(王长清和祝西里,2011).显示算法不需要计算逆矩阵,但为满足稳定性条件,时间步长必须很小,选择显式算法有极大的计算量.根据瞬变电磁场前期变化剧烈、后期变化则相对平缓的特点,本文选择时间步长可逐渐增大的Newmark法进行求解.
该方法原理如下,设t时刻的A(t)已经求得,则t+Δt时刻
(21)
(22)
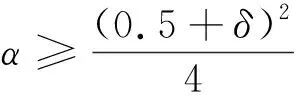
(23)
针对系数矩阵为对称稀疏矩阵的特点,对(23)式的求解,采用针对稀疏矩阵的Intel MKL PARDISO求解器直接求解.
2 算法验证
2.1 均匀半空间
均匀半空间模型的大小为6 km×6 km×6 km,其中空气层厚度2 km,电导率10-12S·m-1,岩石厚度4 km,电导率0.01 S·m-1,发射线框为边长100 m的正方形,水平置于岩石和空气交界面(z=0)的中心,接收线圈面积100 m2,发射电流20 A,电流下降缘波形设为指数下降(如图3所示),关断时间10-5s.
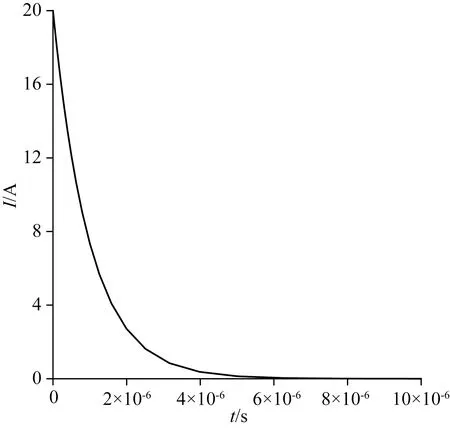
图3 电流关断波形Fig.3 Waveform of the turn-off current
模型的网格剖分采用约束Delaunay算法,共剖分3764个单元,起始时间步长设为10-10s,每5次将步长放大100.1倍,共计算336步,在CPU为i5-8250U,内存8GB的笔记本电脑上,计算时间为164 s.计算完成后通过插值提取了按对数等间距分布的10-5s至0.01 s共31个时间门的数据,并将其与解析解进行对比(如图4所示),除一个时间门的相对误差稍大于3%外其余时间门的相对误差的绝对值均小于3%,31门数据的均方相对误差为1.37%,两者吻合良好,证明了本文算法正确.
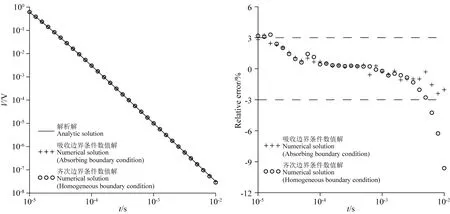
图4 均匀半空间数值解及其相对误差(σ=0.01 S·m-1, 6 km×6 km×6 km)Fig.4 Numerical solution and relative errors of homogeneous half-space (σ=0.01 S·m-1, 6 km×6 km×6 km)
其他设置不变的情况下,将吸收边界条件替换为齐次边界条件(即强制式(11)中的面积分部分为零),此时的数值解与吸收边界条件相比,早期的精度基本一致,但随着时间的增加,电磁场逐渐向边界扩散,误差也逐渐增大,最大相对误差接近-10%,在晚期的精度显著低于吸收边界条件.
图5为均匀半空间模型尺寸为10 km×10 km×10 km(其中空气层厚3 km)时,采用齐次边界条件得到的数值解与解析解的对比,计算时间为231 s.31门数据的均方相对误差为1.38%,与采用吸收边界条件、模型大小为6 km×6 km×6 km时的精度相近.

图5 均匀半空间数值解及其相对误差(σ=0.01 S·m-1, 10 km×10 km×10 km)Fig.5 Numerical solution and relative errors of homogeneous half-space (σ=0.01 S·m-1, 10 km×10 km×10 km)
通过以上对比可见,采用吸收边界条件确实可以缩小模型尺寸、加快正演速度,提高正演的精度.
2.2 H型地电断面
将H型地电断面模型、中心回线装置的数值解与CR1Dmod一维正演程序的结果进行对比,进一步验证本文算法的正确性.模型围岩的电导率为0.01 S·m-1,其中有一顶部埋深80 m、厚20 m、电导率0.1 S·m-1的低阻层,其余设置与均匀半空间模型相同.网格剖分时在发射线框的正下方、低阻层的顶面设置一个正方形以控制该层的网格剖分,改善求解精度(任政勇和汤井田,2009).由于低阻层及其附近需要剖分较小尺寸的网格,因此单元数较均匀半空间大幅增长,共剖分16528个单元.在10-4s之前,时间步长的设置与均匀半空间模型相同,10-4s之后,可以认为受低阻层的影响,电磁场的扩散速度变慢,因此每5次将步长放大100.2倍,共计算294步,计算时间为3720 s.
由图6可见,有限元解和CR1Dmod解在早期偏离较大,在0.01 ms时相对误差接近25%,这是因为受发射电流“暂态效应”的影响,早期场值与关断时间为零的理想条件(CR1Dmod即采用此种假设)相比会有明显的增大(白登海和Maxwell,2001).此后,随着时间的增加,暂态效应的影响降低,有限元解和CR1Dmod解的相对误差也快速减小,在0.1 ms后,相对误差绝对值小于2.5%,进一步证明了本文算法的正确性.

图6 H型地电断面的有限元解和CR1Dmod解及其相对误差Fig.6 FEM solution and CR1Dmod solution of H type geoelectric section and their relative errors
3 算例分析
3.1 水平低阻异常体
如图7所示,在电导率为0.01 S·m-1的围岩中有一规模为600 m×300 m×20 m、顶部埋深80 m、电导率0.1 S·m-1的低阻异常体,异常体中心在地表的投影为坐标原点,其余设置与均匀半空间模型相同.正演时,在异常体的地表投影基础上外扩200 m范围内(即x:-350至350,y:-500至500),以50 m×50 m的网度、移动中心回线的方式计算不同位置的瞬变电磁响应.根据回线位置的不同,模型剖分的单元数4635~5749个不等,时间步长的设置与均匀半空间模型相同,计算时间为961~1872 s.

图7 水平低阻异常体模型示意图Fig.7 Sketchmap of horizontal low resistivity anomalous body model
图8为水平低阻异常体与前述的H型地电断面、均匀半空间模型在坐标原点O的瞬变电磁响应对比.前两者在0.4 ms之前的响应基本相同,与均匀半空间相比,在0.03~0.06 ms都出现了由于反射波干涉引起的电压低于均匀半空间的Undershoot现象,之后感应电压(V)逐渐高于均匀半空间.0.4 ms之后,水平低阻异常体的响应开始快速下降并最终趋于均匀半空间,而H型地电断面受低阻屏蔽效应的影响,感应电压始终高于均匀半空间.

图8 O点不同模型的瞬变电磁响应Fig.8 TEM response of different models at point O
图9为具有代表性时间门的瞬变电磁响应切片.电流完全关断的时刻(0.01 ms)感应电压随位置有幅度不大的无规律波动,推测是由发射框移动引起的网格剖分的差异造成的.0.05 ms时刻,由于Undershoot现象出现了一片低电压区域,其基本呈椭圆形,与异常体的地表投影相比范围略有扩大,中心区域的电压相比正常值下降约16%.0.4 ms时刻,受异常体影响出现的高电压区域,范围相比异常体的投影有所扩大,与正常值相比,测点在距异常体边缘约50 m处感应电压的增幅大于10%,在异常体边缘电压的增幅大于25%,进入异常体投影后电压开始迅速增长并在达到某一值后趋于平稳,电压增幅最大约为160%.10 ms时刻,随着波场的扩散,异常体的影响减弱,电压趋于均匀.

图9 水平低阻异常体的瞬变电磁响应时间切片Fig.9 Time slice of TEM response of horizontal low resistivity anomalous body model

图10 XZ平面0.05~0.06 ms电流密度变化(a) 均匀半空间; (b) 水平低阻异常体.Fig.10 Change of current density in XZ plane from 0.05 ms to 0.06 ms(a) Homogeneous half-space; (b) Horizontal low resistivity anomalous body model.
下面尝试对Undershoot现象做出解释.根据正演结果,抽取了发射框中心位于O点时,均匀半空间和水平低阻异常体模型在0.05 ms、0.06 ms时刻XZ平面处的电流密度,将两者相减得到前后电流密度变化ΔJ,结果见图10,图示以外的部分尚未被感应涡流的扩散波及或电流密度变化极小.与均匀半空间相比,受低阻异常体的影响ΔJ主要集中于异常体(红色虚线所示)内,上部的ΔJ减小.以10 m×10 m的网格剖分图11中的区域,假设在每个网格内ΔJ是均匀的,并将ΔJ形成的电流环视为磁偶极子,则其在O点引起的磁感应强度变化可按下式计算
(24)
式中ds为网格面积,(y,z)为网格中心坐标.均匀半空间的计算结果为-3.99×10-7T,而低阻异常体为-3.19×10-7T.上面的估算是十分粗略的,因为很多时候并不满足源点和场点之间的距离远大于电流环半径这一磁偶极子的假设条件,但仍在一定程度上说明之所以出现Undershoot现象是因为在某些时段低阻异常体对ΔJ的集中不足以补偿其对上部ΔJ减少的影响.

图11 倾斜低阻异常体模型示意图Fig.11 Sketch map of sloping low resistivity anomalous body model
3.2 倾斜低阻异常体
在前节模型的基础上,将地质异常体倾角调整为30°,维持异常体顶面的中心O′至原点O的距离仍为80 m.正演时,以50 m×50 m的网度计算x:-250至250、y:-400至400矩形区域内的瞬变电磁响应.根据回线位置的不同,模型剖分的单元数5349~8792个不等,时间步长的设置与均匀半空间模型相同,计算时间为1117~2616 s.
从图12可见,倾斜和水平低阻异常体在O点的瞬变电磁响应基本相同,只是由于倾斜低阻异常体的垂向等效厚度增大,在0.05~0.2 ms 之间感应电压有7%~18%的提升.

图12 O点水平和倾斜低阻异常体模型的瞬变电磁响应Fig.12 TEM response of models of horizontal and sloping low resistivity anomalous body at point O
y=0线的多测道剖面见图13,图中只显示了部分具有代表性的时间门.0.05 ms时刻,感应电压随x坐标的增长呈先降后升的波浪式起伏;0.1~0.8 ms之间,感应电压呈不对称的单波峰形态,波峰偏向于异常体埋深较浅的一侧并随时间的增加向中心移动且振幅逐渐减小;1.6 ms 时,感应电压在异常体投影范围内有一定的升高但开始趋于均匀.
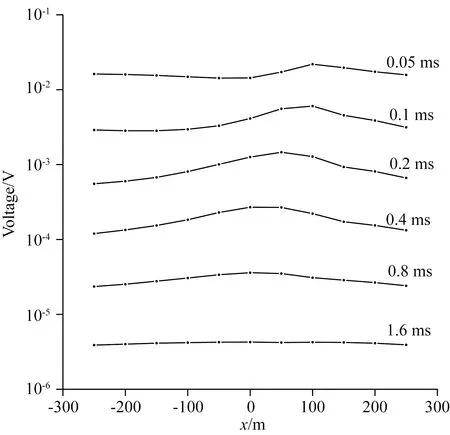
图13 y=0线瞬变电磁多测道剖面Fig.13 TEM multichannel profile of y=0 line
图14为具有代表性时间门的瞬变电磁响应切片.0.01 ms时刻,在异常体埋深较浅的一侧出现了一片低电压条带.0.05 ms时刻,在异常体投影范围内,埋深较浅的一侧呈现高电压,较深一侧呈现低电压,且高压升幅大于低压降幅.0.4 ms时刻,感应电压的变化与水平低阻异常体的特征基本相同,但是电压最大增幅更大(约180%)且波峰偏向于异常体埋深较浅一侧.10 ms时刻,电压的分布基本均匀.
4 结论
(1)从时间域麦克斯韦方程组出发,推导了基于矢量势的微分控制方程,在此基础上结合一阶球面波吸收边界条件推导了弱形式方程,采用一阶四面体矢量单元进行单元分析、带“数值阻尼”的Newmark法进行时间离散、并将回线源视为多个电偶源的策略,实现了任意发射电流波形的瞬变电磁法响应的时间域快速求解.
(2)通过有限元数值解与均匀半空间模型的解析解、H型地电断面模型的CR1Dmod解的对比,证明了本文算法的正确性.均匀半空间模型采用吸收边界条件和齐次边界条件的结果对比则表明:吸收边界条件确实可以提高瞬变电磁法三维正演的精度或者缩小模型尺寸、加快计算速度.
(3)根据正演结果,其他条件相同时,水平有限体积的低阻异常体和H型地电断面的瞬变电磁响应前期基本相同,但在晚期前者会快速趋于均匀半空间的响应.对比均匀半空间和水平低阻异常体模型在0.05 ms、0.06 ms时刻电流密度的变化,表明感应电压的Undershoot现象之所以出现,是因为低阻异常体对电流的集中不足以补偿其引起的上部电流减少的影响.对于倾斜低阻异常体,由于垂向上等效厚度增大,中心处的感应电压会高于相同条件的水平低阻异常体,在沿倾向的多测道剖面上感应电压的波峰会向异常体埋深较浅的一侧偏移.
致谢中国地质大学(武汉)胡祥云教授、中国科学院地质与地球物理研究所安志国副研究员对本文提出了有益的建议,在此表示感谢.此外,对审稿人提出宝贵的修改意见和编辑们的辛苦工作表示感谢.

