基于微观孔隙结构特征的速度频散和衰减模拟

欧阳芳， 赵建国*， 李智， 肖增佳， 贺艳晓， 邓继新， 赵皓， 任静

1 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249 2 成都理工大学油气藏地质及开发工程国家重点实验室， 成都 610059

0 引言

当地震波在地下介质中传播时会在很宽的频率范围和空间尺度上诱发速度频散和衰减，而发生在孔隙尺度上的流体流动，我们将之称为喷射流.喷射流通常由相邻孔隙刚度差异形成的局部压力梯度所引起，故又称为局部流.这种局部或孔隙尺度的喷射流现象一般出现在超声频段，但也可能在测井和地震频段发挥着一定的作用(Johnston et al., 1979; Sams et al., 1997; Pride et al., 2004).

喷射流理论最早由Mavko和Nur(1975)基于非均匀介质的单一孔隙提出，后经Palmer和Traviolia(1980)、O′Connell(1984)、Murphy等(1986)、Mavko和Jizba(1991)、Dvorkin等(1995)、Gurevich等(2009, 2010)的发展，形成了模拟孔隙尺度局部流体流动的一系列喷射流模型.20世纪90年代初，Dvorkin和Nur(1993)将“宏观Biot机制”与“微观喷射机制”结合起来，建立了BISQ模型.该研究发现，由于微观喷射流的影响，BISQ模型预测的速度频散及衰减比经典Biot模型的预测结果大得多，且与实测数据量级更为吻合.Dvorkin和Nur(1993)认为，喷射流是造成地震波大规模衰减和频散的重要原因.在国内，聂建新(2004)、申义庆和杨顶辉(2004)和杨宽德等(2002,2011)基于BISQ理论对双相介质的波传播特征进行了深入研究，并分析了Biot流与喷射流动力学机制之间的关系.然而，BISQ理论也存在一些显著问题：其低频极限与公认的Gassmann方程不一致，且BISQ理论公式中存在实验室不可测量的特征射流长度参数，因此该理论的实际应用在一定程度上受到了限制.

另一方面，诸多研究表明，喷射流引起的速度频散和衰减大小与岩石孔隙结构参数密切相关，尤其是孔隙纵横比，只有纵横比很小的裂缝或微裂隙才会引起显著衰减，而纵横比较大的孔隙(如等径孔)对衰减几乎没有什么贡献(Jones, 1986).在微裂隙喷射流效应的模拟方面，常用的方法是假设岩石孔隙空间由两部分构成：体积含量占主导的硬孔隙和对压力变化十分敏感的微裂隙或软孔隙(Walsh, 1965; Shapiro, 2003).Mavko和Jizba(1991)基于此假设条件，提出了一种“湿骨架”模型，即软孔隙饱含流体而硬孔隙为空的岩石，以此量化极高频条件下喷射流产生的弹性响应.大量测试结果表明，Mavko-Jizba模型估计的高频模量与实验数据具有良好的一致性(Mavko and Jizba, 1994; Wulff and Burkhardt, 1997).之后，Dvorkin等(1995)利用BISQ理论解释软孔隙部分的喷射作用，成功地将Mavko-Jizba模型扩展到全频段，但也由于BISQ理论的应用，该模型的理论公式中存在实验不可测量的特征射流长度参数.

相较之下，Gurevich等(2010)提出的喷射流模型最为经典，适用范围也最为广泛.Gurevich喷射流模型是基于Murphy等(1986)的压力松弛方法与Sayer和Kachanov(1995)的间断张量公式建立的，该模型假设微裂隙为具有相同孔隙纵横比的硬币形椭球状孔隙，且其四周与硬孔隙相连.在Gurevich喷射流模型中，微裂隙与硬孔隙之间的喷射流作用由流体的等效复体积模量表征，而硬孔隙之间的流体流动则由Gassmann或Biot理论描述.由于经典Gurevich喷射流模型只考虑单一纵横比软孔隙与硬孔隙之间的喷射作用，De Paula等(2012)基于从干燥岩石速度-压力曲线中提取的软孔及中孔的等效孔隙纵横比，进一步将其扩展到包含软孔与中孔以及中孔与等径硬孔流体流动效应的情形.在国内，邓继新等(2015)基于储层砂岩的微观孔隙结构特征，分析了喷射流引起的弹性波频散响应，并尝试通过多次迭代的方式将不同纵横比的软孔隙引入经典Gurevich模型中，但这种方法仅从数学的角度加入了多种软孔隙的影响，而并不具有明确物理含义.之后，Duan等(2018)对该方法进行了改进，利用软孔隙之间不存在流体流动的无相互作用近似，引入了硬孔隙与不同纵横比软孔隙之间的喷射流效应.

从上可知，尽管现有喷射流模型充分考虑了微裂隙和硬孔隙之间的局部流体流动，但却忽略了微裂隙与微裂隙之间的喷射作用.基于此，本文对经典Gurevich喷射流模型进行了扩展，利用基于虚拟降压的孔隙纵横比反演策略(欧阳芳等, 地球物理学报, 已接收)从干燥岩石超声速度-压力曲线中提取出不同有效压力下的微裂隙孔隙纵横比分布，进而得到岩石中各种微裂隙的体积压缩系数；然后，在此基础上，利用孔隙空间的压力松弛效应模拟微裂隙与微裂隙间的喷射流效应.

1 Gurevich喷射流模型

设岩石孔隙空间由相互连通的硬孔隙和微裂隙(或软孔隙)构成，岩石的总孔隙度为φ=φs+φc≈φs，其中φs为硬孔隙度，φc为微裂隙的总孔隙度且φc≪φs，岩石矿物基质的体积模量和剪切模量分别为Km和Gm，干骨架弹性模量为KD和GD，岩石渗透率为κ.Gurevich等(2010)的研究表明，在考虑了微裂隙与硬孔隙喷射流效应的条件下，岩石“湿骨架”的频率相关弹性模量Kwf和Gwf可以写成如下解析形式：

(1)

以及

(2)

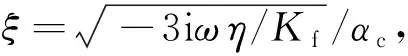
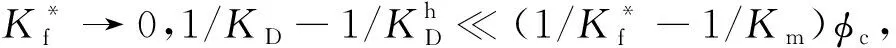
Kwf(P,0)=KD(P),Gwf(P,0)=GD(P),

(3)

在高频极限条件下，ξ→，故→Kf，于是，有

(4)

(5)

实际上，Grevich高频极限公式是Mavko-Jizba方程的扩展，且适用于任意孔隙流体条件，而经典的Mavko-Jizba公式仅适用于孔隙流体为纯液体的情形.

在Gurevich模型中，饱和岩石的动态弹性模量是通过将岩石的“湿骨架”模量Kwf和Gwf代入Gassmann方程得到的，因此并没有考虑Biot宏观流动.这里为了描述硬孔隙之间的宏观流动效应，我们采用Biot孔弹性理论.于是，速度频散和衰减计算公式为

V=1/Re(1/Vc),Q-1=Im(Vc2)/Re(Vc2),

(6)

式中，V为相速度；Q-1为品质因子倒数；Vc表示由Biot模型计算的复纵波或横波速度，即(Stoll, 1977; Mavko et al., 2009)

(7)

式中，

(8)

其中，Kwf和Gwf为包含喷射流作用的岩石湿骨架模量；ρf为孔隙流体密度；η为流体黏度；κ为渗透率；ρD为干燥岩石的密度；a为曲折度，对于一个具有所有可能分布的孔隙的随机系统，a=3(Stoll, 1977).

2 喷射流模型的扩展

经典Gurevich喷射流模型只考虑了一种纵横比(αc)的软孔隙与硬孔隙之间的局部流体流动(见式(1)—(2))，下面我们将在此基础上引入不同纵横比微裂隙之间的喷射流效应.

2.1 模型扩展

假设岩石中仅含一种孔隙纵横比为αc的微裂隙，其孔隙度为φc，则在有效压力P下，此种微裂隙的体积压缩系数Cp(P)满足(Zimmerman, 1991)

(9)

(10)

为了方便理解，我们首先假设岩石中含有两种类型的微裂隙，其压缩系数分别为Cp1和Cp2，孔隙度为φ1和φ2，孔隙纵横比为α1和α2，且α1>α2.当波穿过岩石时，纵横比较小的微裂隙α2对压力变化更为敏感，在流体压力梯度的作用下最先闭合，从而将其内部流体挤入至纵横比较大的微裂隙中.因此，两种微裂隙之间的喷射流效应可以利用式(10)表示为

(11)

式中，K1为微裂隙α2所在背景介质的体积模量，包含了矿物基质、硬孔隙和微裂隙α1的综合影响.当微裂隙α2闭合后，纵横比相对较大的微裂隙α1也随之闭合，而此时岩石中仅硬孔隙处于开孔状态，于是微裂隙α1中的流体会向硬孔隙发生喷射.因此，K1的具体形式可以写成

(12)

联立式(11)—(12)，得到

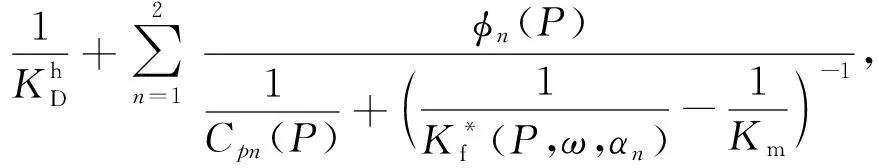
(13)

这是综合考虑了微裂隙α1、微裂隙α2以及硬孔隙之间局部流体流动效应的岩石湿骨架模量.

对于存在N种微裂隙的情形，我们可以很容易由式(13)得到相应的推广公式，即

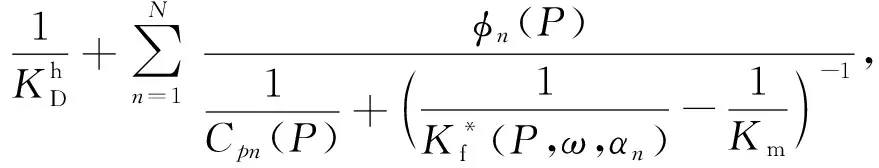
(14)

式中，φn(P)，αn(P)和Cpn(P)表示有效压力P下第n种微裂隙的孔隙度、纵横比和体积压缩系数，其中φn和αn基于孔隙结构模型和各种等效介质理论直接从干燥岩石的超声速度-压力数据中反演得到，具体反演方法参见附录.

对于孔隙压缩系数Cpn，我们可以利用如下关系获得(Zimmerman, 1991; David and Zimmerman, 2012)：

(15)

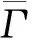
(16)

将式(16)代入式(14)中，最后有

(17)

这就是扩展后的Gurevich“湿骨架”公式，该模型不仅描述了微裂隙与硬孔之间的局部流体流动，还依据孔隙纵横比的大小加入了N种微裂隙之间的喷射流效应.注意，扩展模型的剪切模量计算公式与经典Gurevich“湿骨架”模型一致，只需利用式(17)计算的Kwf替换式(1)中的Kwf即可.扩展Gurevich喷射流模型的速度频散和衰减计算流程见图1.

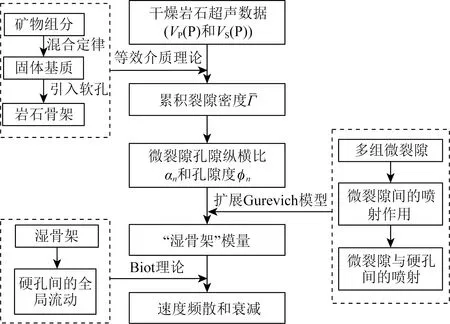
图1 扩展Gurevich喷射流模型的速度频散和衰减计算流程Fig.1 Workflow for calculating velocity dispersion and attenuation using extended Gurevich squirt model

2.2 高低频极限

(18)

为验证扩展模型的低频极限为Gassmann方程，只需证明湿骨架体积模量Kwf(P,ω)的低频极限等于干岩骨架的体积模量KD，换而言之，证明如下关系成立即可：

(19)

根据Zimmerman(1991)，累积裂隙密度可以写成如下微分形式：

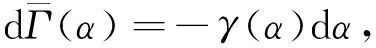
(20)

式中，α为微裂隙纵横比；γ(α)为裂隙密度关于孔隙纵横比的分布函数，其与孔隙度分布函数c(α)之间的关系为

(21)

注意，c(α)dα的离散形式为孔隙度φn(Zimmerman, 1991).于是，联立式(20)—(21)，得到

(22)

因此，在低频极限条件下，湿骨架模型等于干骨架模量：

Kwf(P,0)=KD(P),

(23)

由此证明了扩展模型的低频极限为Gassmann方程.

(24)

由此可见，在孔隙流体为液体的条件下，扩展Gurevich“湿骨架”模型的高、低频极限与经典模型一致，仍为Mavko-Jizba和Gassmann方程.

3 模型应用

3.1 超声饱和速度预测

根据工作流程图1，我们可以基于扩展Gurevich喷射流模型预测弹性波的速度频散和衰减.由流程图可见，岩石微观孔隙结构参数(即累积裂隙密度、孔隙纵横比和孔隙度)还与等效介质理论的选取有关，为了分析不同等效介质理论的影响，我们先以1块枫丹白露砂岩样品S1和1块致密灰岩样品C1为例，对比基于KT、MT、DEM和SCA四种等效介质理论从干燥岩芯的超声数据中反演得到微裂隙的孔隙纵横比和孔隙度分布(图2).

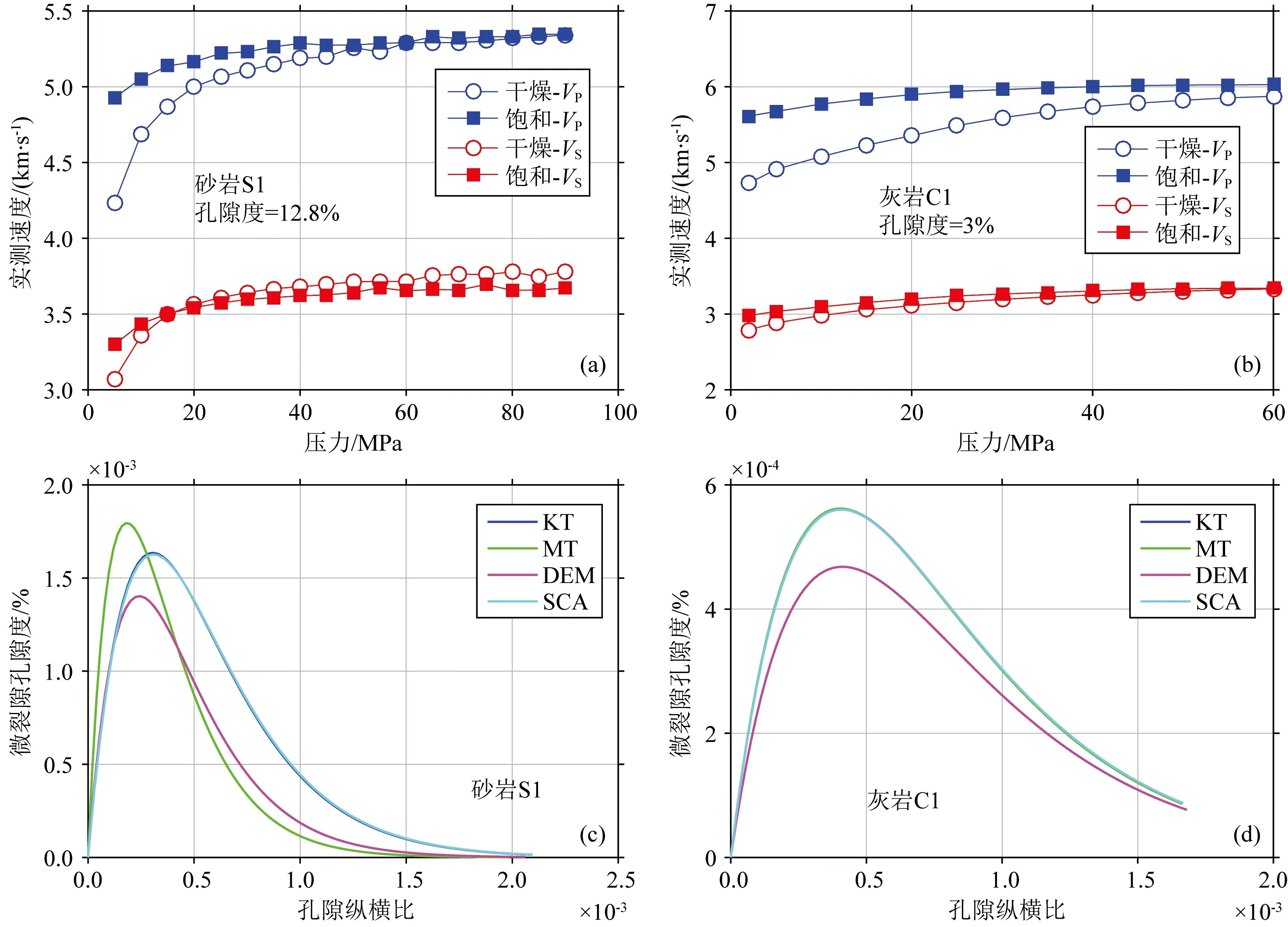
图2 岩石样品的超声实验数据与孔隙结构参数反演结果(a) 砂岩超声实验数据； (b) 灰岩超声实验数据； (c) 砂岩微裂隙孔隙度分布； (d) 灰岩微裂隙孔隙度分布.Fig.2 Measured ultrasonic data and inverted pore structrue parameters for rock samples(a) Measured ultrasonic data for sandstone; (b) Measured ultrasonic data for limestone; (c) Crack porosity distribution of sandstone; (d) Crack porosity distribution of limestone.

图2a—b展示了干燥和饱水条件下砂岩样品S1和灰岩样品C1在不同有效压力处纵横波速度的超声实验测量结果，其中砂岩样品S1的数据来自于文献David(2012)，其矿物成分为100%的石英，孔隙度为12.8%，干燥岩石密度为2309 kg·m-3，渗透率为190 mD；灰岩样品C1的矿物成分为100%的方解石，孔隙度为3%，干燥岩石密度为2589 kg·m-3，渗透率为0.06 mD.从图中可以看出，在低有效压力范围内，砂岩样品的纵横波速度曲线比灰岩样品具有更强的非线性特征.图2c—d给出了基于KT、MT、DEM和SCA四种等效介质理论反演得到的微裂隙孔隙度-孔隙纵横比曲线.由图可见，基于不同等效介质理论反演的孔隙结构参数在数值上存在略微差别，但四种模型估计的孔隙纵横比范围及孔隙度变化趋势基本一致，其中砂岩S1的微裂隙孔隙纵横比主要分布在区间[0,0.001]上，其最大孔隙度约为0.0016%，总孔隙度φc约为0.04%；而灰岩C1的微裂隙孔隙纵横比主要分布在区间[0,0.0015]，其最大孔隙度约为0.0006%，微裂隙总孔隙度φc约为0.03%.

将不同等效介质理论反演得到的孔隙结构参数代入扩展Gurevich喷射流模型中(公式(24))，进一步计算超声频率1MHz条件下的饱和岩石速度.图3对比了完全饱水条件下砂岩样品S1和灰岩样品C1的实验测量数据与模型预测结果，图中Biot是指由实测干燥岩石数据和经典Biot理论计算的饱和速度；KT-Gurevich、MT-Gurevich、DEM-Gurevich、SCA-Gurevich分别表示利用扩展Gurevich喷射流模型与KT、MT、DEM、SCA四种等效介质理论反演的孔隙结构参数预测的饱和速度.由图可见，基于四种等效介质理论和扩展模型计算的饱和岩石速度几乎是完全一致的.这意味着，尽管不同等效介质模型反演的孔隙结构参数存在一定差异(见图2c—d)，但这种差异并不影响饱和速度的最终预测结果.由此可见，等效介质理论选取对扩展Gurevich喷射流模型的影响几乎可以忽略不计.此外，从图中还可以看出，由扩展Gurevich喷射流模型预测的饱和速度与超声实验数据吻合很好，而经典Biot理论的估值则严重偏低，尤其是在低有效压力范围.

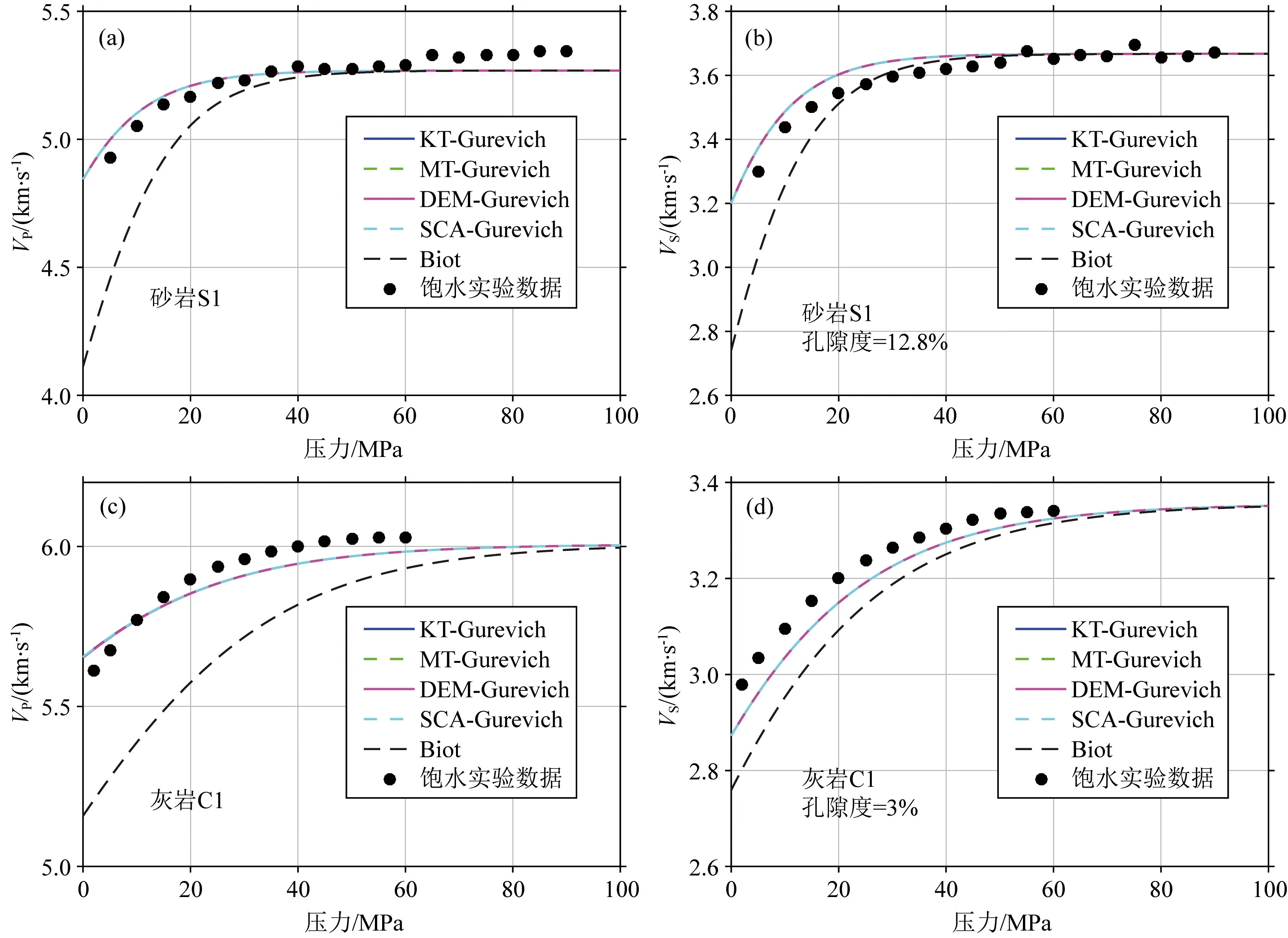
图3 超声频率条件下实验测量数据与模型预测结果比较(a) 饱水砂岩S1的纵波速度； (b) 饱水砂岩S1的横波速度； (c) 饱水灰岩C1的纵波速度； (d) 饱水灰岩C1的横波速度.Fig.3 Comparision of measured velocities and predictions obtained from different models at ultrasonic frequency(a) P-velocity of water-saturated sandstone S1; (b) S-velocity of water-saturated sandstone S1; (c) P-velocity of water-saturated limestone C1; (d) S-velocity of water-saturated limestone C1.

为了从统计分析的角度进一步说明扩展Gurevich喷射流模型的可靠性，我们利用该模型对31块泥质砂岩样品和40块致密灰岩样品的超声纵横波速度进行了预测(见图4)，其中砂岩样品的主要矿物成分为石英、长石、方解石、白云石和粘土，孔隙度分布范围为3.5%～30%；灰岩样品主要由方解石构成，其孔隙度分布范围为0.3%～3%.从图4中可以看出，对于泥质砂岩样品和大部分致密灰岩样品，扩展Gurevich喷射流模型(图中实心点)均能给出与实测数据吻合良好的预测结果，仅少数灰岩样品的速度模拟值严重偏低；无论是砂岩还是灰岩，Biot模型(图中空心点)均低估了样品的纵波速度，而Biot模型预测的横波速度与扩展Gurevich喷射流模型差异不大.此外，结合岩芯柱体薄片信息发现，模型预测精度较高的岩芯样品一般具有孔隙或微裂缝发育良好且孔隙分布均匀等特征，如图4中的样品A，其薄片分析结果见图5a,c；而模型预测精度较低的岩芯样品则通常孔隙局部富集发育或孔隙局部不发育，如图4中的样品B，其薄片分析结果见图5b,d.

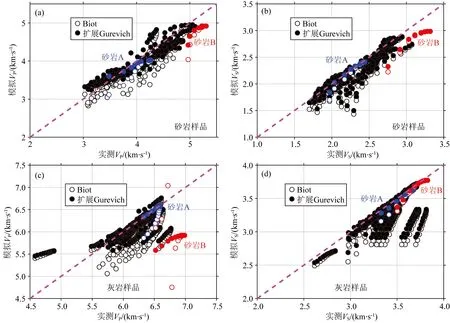
图4 饱水条件下所有岩芯样品的模型计算结果与超声实验速度比较(a) 所有砂岩样品的纵波速度； (b) 所有砂岩样品的横波速度； (c) 所有灰岩样品的纵波速度； (d) 所有灰岩样品的横波速度.Fig.4 Ultrasonic velocity measurements and model predictions at water-saturated condition(a) P-velocity for sandstones; (b) S-velocity for sandstones; (c) P-velocity for limestones; (d) S-velocity for limestones.

图5 代表性砂岩和灰岩样品的柱体薄片Fig.5 Thin sections for representative sandstone and limestone samples

3.2 速度频散和衰减预测

为了更好地理解扩展Gurevich喷射流模型，我们首先分析一组微裂隙发生喷射所引起的速度频散及衰减特征，即经典喷射流理论.图6展示了经典Gurevich喷射流模型的速度频散及衰减随微裂隙孔隙纵横比αc与总孔隙度φc的变化规律.由图可见，经典Gurevich喷射流模型预测的速度频散曲线存在明显的快速变化特征，即速度由低频极限迅速过渡到高频极限，过渡频率区间十分窄小.从图6还可以看出，经典喷射流模型的特征频率随孔隙纵横比和孔隙度的增加逐渐向高频移动，这一规律也可以通过喷射流特征频率的定义获得，即(Gurevich et al., 2010)

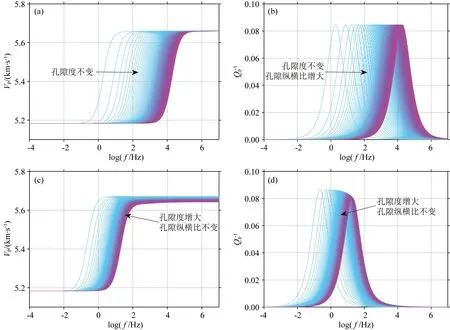
图6 经典Gurevich喷射流速度频散与衰减曲线随微裂隙孔隙纵横比与孔隙度的变化规律Fig.6 Squirt velocity dispersion and attenuation predicted by classical Gurevich model as a function of crack aspect ratio and porosity

(25)

由上式可见，ωc随αc的增大而增大；而当微裂隙孔隙度增大时，岩石变“软”，即干燥岩石体积模量KD减小，从而也导致特征频率向高频移动.需要十分注意的是，图6c—d表明，微裂隙孔隙度的增加还会造成速度高频极限和衰减峰值的降低.

通过上述分析可知，经典Gurevich模型是将岩石中所有的微裂隙等效为一组纵横比相同的孔隙，然后基于此组微裂隙的等效纵横比αc与总孔隙度φc来预测饱和岩石的速度频散和衰减.然而，这种做法在一定程度上模糊了岩石的微观孔隙结构特征.与经典模型不同，扩展Gurevich模型以岩石中所有微裂隙的孔隙纵横比和孔隙度作为输入，从而综合考虑了各组微裂隙的孔隙结构特征对岩石速度频散和衰减的影响.

根据从干燥岩石超声数据反演得到的孔隙结构参数，我们可以利用扩展Gurevich喷射流模型预测出饱和岩石在整个地震-测井-超声频段范围的速度频散和衰减.图7展示了0 MPa有效压力下扩展Gurevich喷射流模型依据孔隙纵横比由小到大的次序加载微裂隙的过程，并将其与经典喷射流模型进行了对比.由图可见，随着越来越多微裂隙的加入，扩展模型的纵波速度变化趋势随频率的增加而逐渐减缓，其高频极限向更高的频率移动，且速度高频极限减小；衰减也逐渐降低，且衰减峰值也向高频移动，而衰减发生的频率范围逐渐扩大.这是因为在微裂隙的加载过程中，孔隙纵横比逐渐变大，所以在高纵横比微裂隙特征频率的影响下，频散曲线逐渐向高频方向倾斜，频率过渡区间也随之变宽；另一方面，微裂隙的数量也在增加，即微裂隙总孔隙度变大，故速度高频极限和衰减峰值降低.需要注意的是，经典模型与扩展Gurevich喷射流模型的高频极限相同，且在加入微裂隙的过程中，此高频极限随微裂隙总孔隙度的增加而降低.因此，扩展模型速度频散曲线的高低频极限始终与经典Gurevich喷射流模型保持一致；换而言之，扩展模型的低、高频极限始终为Gassmann和Mavko-Jizba方程.与仅考虑一种孔隙纵横比(α=3.6×10-4)的经典模型相比，扩展模型的速度频散曲线在更宽的频段范围由低频(10-4Hz)至高频(106Hz)呈缓慢的增加趋势.

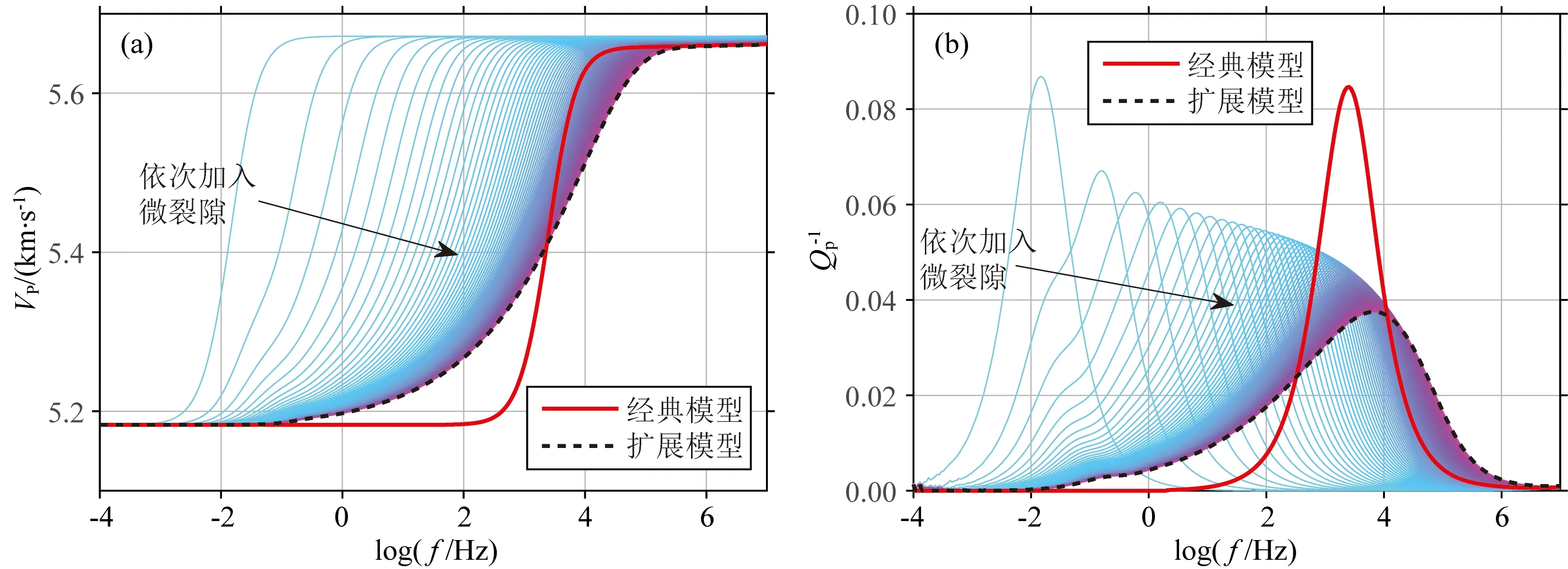
图7 0 MPa有效压力下饱水灰岩样品C1的纵波速度频散(a)和衰减(b)Fig.7 P-velocity dispersion and attenuation for water-saturated limestone sample C1 at 0 MPa

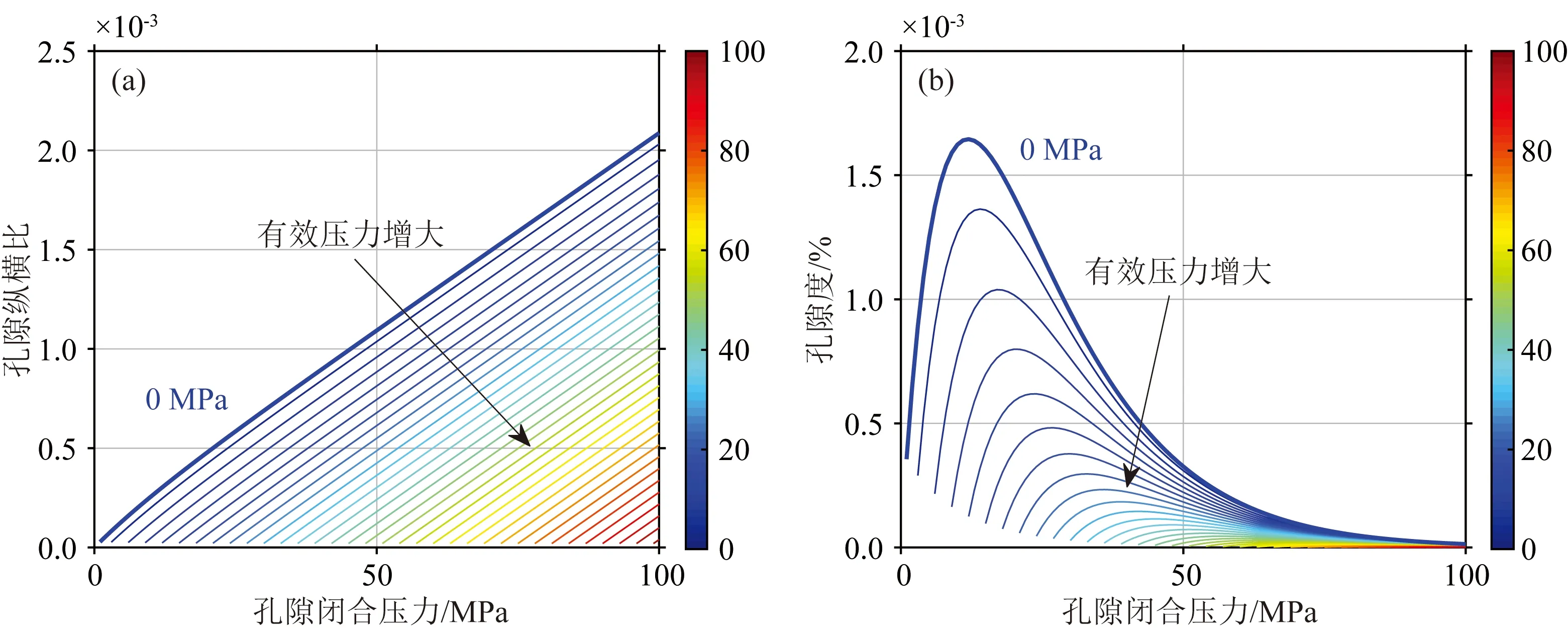
图8 不同有效压力灰岩样品C1中微裂隙的孔隙纵横比分布(a)和孔隙度度分布(b)Fig.8 Aspect distribution (a) and porosity distribution (b) of limestone sample C1 at different pressure

下面我们以砂岩样品S1为例，基于扩展Gurevich喷射流模型分析岩石孔隙结构变化对速度频散和衰减的影响.图8给出了由干燥砂岩样品S1超声数据反演得到的不同有效压力下(0～100 MPa)的微裂隙孔隙度分布和纵横比分布.图中横坐标为岩石中各组微裂隙对应的闭合压力，纵坐标分别为这些微裂隙的孔隙纵横比和孔隙度；蓝色粗实线表示0MPa有效压力下的微裂隙孔隙纵横比和孔隙度分布曲线；黑色箭头指示有效压力的增大方向.由图可见，在0MPa有效压力下，孔隙闭合压力很小的微裂隙的孔隙度和纵横比并不为零，这说明所有的微裂隙均处于开孔状态；随着有效压力的增大，纵横比和孔隙度分布曲线逐渐向右下方移动，且分布范围逐渐向高闭合压力方向收缩，这意味着：有效压力增大后，岩石中孔隙闭合压力小于当前有效压力的微裂隙将完全闭合，仅闭合压力较大的微裂隙仍处于开孔状态，而受施加压力的影响，这些开孔微裂隙同时也会被压缩，故其孔隙度和纵横比降低.

图9 砂岩S1的纵横波速度频散(a—b)及衰减(c—d)曲线Fig.9 P- and S-velocity dispersion (a—b) and attenuation (c—d) as a function of frequency and pressure for sandstone sample S1

图9为由扩展Gurevich喷射流模型预测的砂岩样品S1的纵横波速度频散和衰减.图中各有效压力下的速度频散和衰减曲线分别对应于图8中相应压力下的微裂隙纵横比和孔隙度分布，因此每一条频散和衰减曲线都可视为由不同孔隙结构造成的结果.由图9可见，纵横波速度随着频率的增加呈逐渐上升趋势，并在f=105Hz处到达其高频极限；而衰减曲线则随着频率的增加先上升后下降，且在f=1000 Hz处取得最大值；但无论是速度频散还是衰减，其变化程度均随有效压力的增加而减小.此外，从图中还可以看出，在低有效压力范围内，衰减曲线存在两处峰值，其对应的频率位置分别为f=0.5 Hz和f=1000 Hz，这是因为当压力较低时，岩石中存在大量未闭合的微裂隙，在这种情况下孔隙尺度的喷射流机制起主要作用.但随着压力的继续增加，微裂隙逐渐闭合，喷射流效应也随之消失，硬孔隙之间的Biot宏观流动逐渐占主导，当压力到达100 MPa时，饱和岩石中的微裂隙已全部闭合，此时速度频散和衰减的大小刚好等于Biot模型的估计值(见图9红色实线)，且其特征频率为105Hz.另外，根据扩展模型的预测结果可见，喷射流机制引起的速度频散和衰减在1～10 kHz(测井频段)附近最为显著，同时也在地震频段发挥着一定作用.

类似地，我们还计算了完全饱水条件下灰岩样品C1的纵横波速度频散和衰减(见图10).由图10可见，灰岩速度频散及衰减随压力和频率的总体变化趋势与砂岩类似，只是其Biot特征频率并没有出现在频率范围10-2～106Hz内.此外，从图中可以看出，纵波衰减比横波衰减略大，且两者衰减峰值出现的频率位置不同，其中纵波衰减峰值出现在f=104Hz附近，而横波衰减则出现在f=103Hz附近.

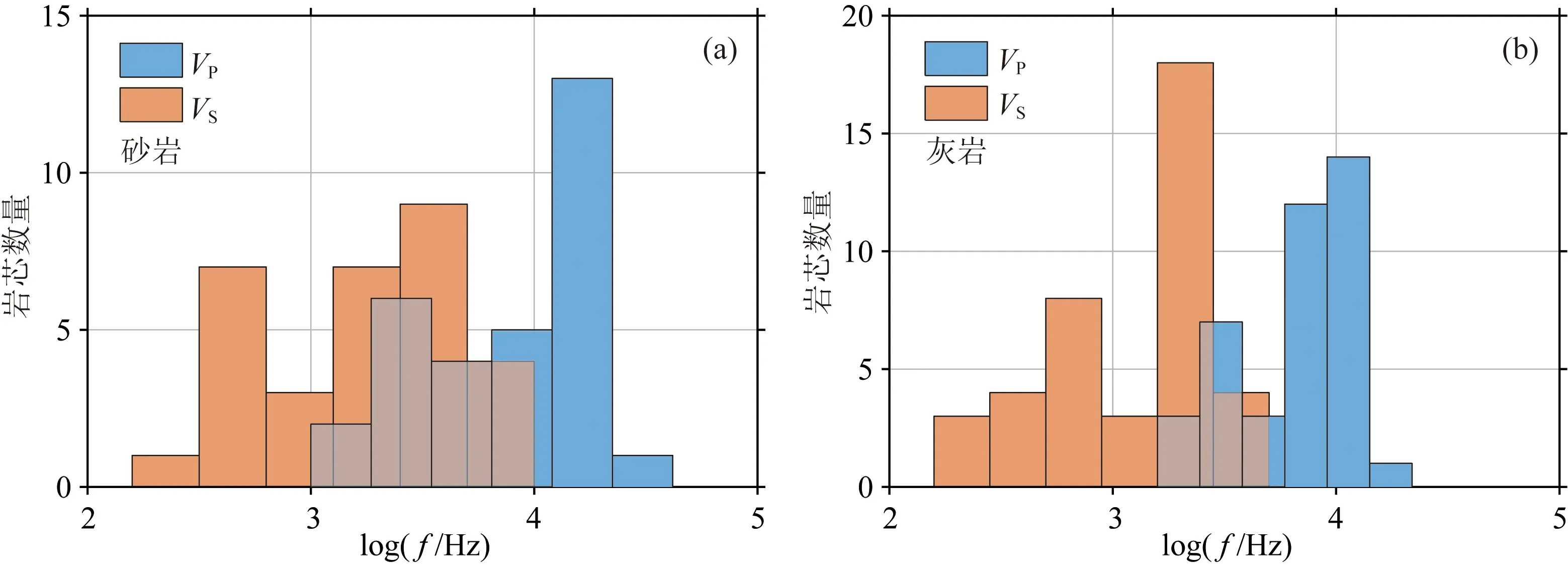
图11 砂岩(a)和灰岩(b)纵横波衰减峰值频率的统计直方图Fig.11 Histogram of frequencies corresponding to attenuation peak of P- and S-waves for sandstones (a) and limestones (b)

图11统计了所有31块泥质砂岩和40块致密灰岩样品的纵横波衰减峰值频率.从图中可以看出，无论是砂岩还是灰岩，横波衰减峰值出现的频率普遍低于纵波，其中灰岩尤为明显.另外，在31块砂岩样品和40块灰岩样品中，19块砂岩和26块灰岩的纵波衰减峰值均出现在测井频段(～10 kHz)，而17块砂岩和28块灰岩的横波衰减峰值则出现在f=103Hz附近，此模拟结果表明着喷射流机制在地震和测井频段发挥着重要作用.

4 结论

基于从干燥岩石超声速度-压力曲线中提取出的微裂隙孔隙纵横比分布，推导了微裂隙的体积压缩系数计算公式，并在此基础上，利用孔隙空间的压力松弛效应，将不同孔隙纵横比的微裂隙的喷射作用引入经典Gurevich喷射流模型中.扩展后的Gurevich模型不仅考虑了硬孔隙和微裂隙的局部流体流动以及硬孔隙和硬孔隙的Biot宏观流，还加入了微裂隙之间的喷射流作用.理论分析和数值计算结果表明，当孔隙流体为液体时，扩展模型的低、高频极限始终与Gassmann方程和Mavko-Jizba方程一致.采用31块砂岩样品和40块致密灰岩样品的超声实验数据，从单块岩芯和统计分析的角度分别对扩展模型的计算结果进行了分析，研究发现：尽管不同等效介质理论反演的孔隙结构参数存在一定差异，但这种差异对饱和速度的预测几乎没有影响.此外，对于所有砂岩样品，模型计算结果与超声实际测量数据均具有良好的一致性，而对于大部分灰岩样品，其模拟结果与实际数据也吻合较好，仅少数灰岩样品被严重低估，但砂岩的预测精度整体上比灰岩更高.另一方面，基于扩展模型计算的速度频散曲线由低频至高频呈逐渐增大趋势，不具有快速变化特征，与经典频散曲线形态存在显著差异.在低有效压力下，由于微裂隙之间的喷射流作用强烈，饱和岩石的速度频散及衰减十分显著，且主要发生在地震和测井频段；而随着有效压力增加，微裂隙逐渐闭合，Biot宏观流机制开始发挥作用，速度频散和衰减逐渐减小并往高频方向移动.

附录 微裂隙孔隙结构参数反演

为了获得微裂隙的孔隙结构参数，如孔隙纵横比、孔隙度和累积裂隙密度，这里我们采用欧阳芳等(2021)提出的基于虚拟降压的反演思路；读者也可以采用David和Zimmerman(2012)给出的经典孔隙结构模型进行反演.实际上，欧阳芳等的虚拟降压反演方法是David-Zimmerman方法的重要补充，后者是基于等效基质理论DEM和MT实现的，而前者在其基础上同时结合了KT、MT、DEM、SCA四种等效介质理论，再借助假想降压过程实现微裂隙孔隙纵横比分布的反演.

根据基于虚拟降压的反演方法，裂隙密度的计算可以通过KT、MT、DEM、SCA四种等效介质理论实现，即

(26)

(27)

(28)

(29)

式中，K、G和ν表示体积模量、剪切模量和泊松比，其上标“*”表示等效介质，下标“b”表示背景介质.按照压力由高至低的顺序，将干燥岩石的弹性模量KD(Pk),GD(Pk)和KD(Pk-1),GD(Pk-1)分别作为背景介质和等效岩石的弹性模量依次代入式(26)—(29)中，反演裂隙密度Γ(Pk)；然后，在此基础上求取累积裂隙密度，即

(30)

将上式代入如下公式，进一步获得微裂隙的孔隙纵横比分布

(31)

以及裂隙密度分布函数γ、孔隙度分布函数c和微裂隙孔隙度φn：

(32)

这里需要注意的是，上述反演方法需要结合等效介质理论才能实现，因此，等效介质理论的选取可能会在一定程度上影响孔隙结构参数的反演结果，具体分析详见文中的“模型应用”部分.