脉冲参量对时间门控光频域反射仪性能的影响

易守天，张志勇，何海军，张信普，钱 恒

(西南交通大学 信息科学与技术学院 信息光子与通信研究中心, 成都 610031)

引 言

相位敏感的光时域反射仪(phase-sensitive optical time domain reflectometer,φ-OTDR) 具有耐腐蚀、抗电磁干扰能力强、灵敏度高等特点，在管道安全检测、桥梁健康检测、周界防护等领域备受关注[1-4]。空间分辨率和传感距离是φ-OTDR系统中的两个重要参量，两者之间存在矛盾，随着脉冲信号脉宽的增加，测量距离增加，系统空间分辨率会降低，因此传统的φ-OTDR很难在长距离传输的情况下实现高空间分辨率。2015年,ZOU等人[5]提出光脉冲压缩反射仪(optical pulse compression reflectometry,OPCR)，采用该方法后系统空间分辨率只与扫频范围相关，不受脉冲宽度的影响，从而解决了空间分辨率与脉宽之间相互约束的问题。同年，LIU等人[6]将光脉冲压缩技术应用到φ-OTDR技术中，得出时间门控光频域反射仪(time-gated digital optical frequency domain reflectometry,TGD-OFDR)在传感距离为110km时,系统空间分辨率达到1.6m。后续学者不断研究完善，进一步提高了TGD-OFDR系统性能[7-12](例如相干衰落抑制、信噪比提升)。

TGD-OFDR系统中，空间分辨率仅与扫频范围相关，而扫频范围取决于脉宽与啁啾率的乘积，增大脉宽或者啁啾率均可提升扫频范围，可以提高空间分辨率。但是，现有文献中并未对脉冲参量(例如脉宽、啁啾率)和系统信噪比与相位噪声之间的关系进行分析。基于上述分析，作者主要围绕探测脉冲的两个主要参量：啁啾率和脉宽进行分析，分别探究了啁啾率、脉宽变化时，系统信噪比和相位噪声的变化情况。

1 系统原理

1.1 TGD-OFDR系统的工作原理

TGD-OFDR系统中，光电探测器(photodetector,PD)接收端接收到的信号可以表示为[8]：

cos[-ωcτi+2πf0(t-τi)+πk(t-τi)2]

(1)

式中,Es(t)表示散射光信号，ELO(t)表示本振信号，t是时间变量,上标*表示复共轭,ai为衰减系数，ri为瑞利散射系数，N表示散射点个数，τi表示第i个散射点对应的时间,τp为脉冲宽度，ωc为光载频，f0为起始频率，k为啁啾率。由于散射点尺寸特别小(小于0.1λ)，所以在脉冲宽度范围内的散射点数目很多,故而(1)式可以转化为：

πk(t-τ)2-ωcτ]}dτ=h(t)⊗s(t)

(2)

式中，τ表示散射点之间的时间差，a和r表示衰减系数和瑞利散射系数,h(t)表示光纤中脉冲响应函数：

h(t)=a(t)r(t)exp[j(-ωct)]

(3)

s(t)为任意函数发生器(arbitrary function generator,AFG)产生的线性扫频信号：

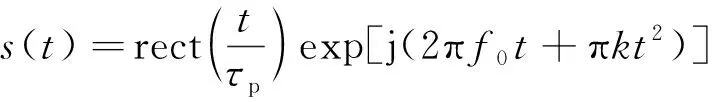
(4)

通过匹配滤波器之后信号转化为：

y(t)=i(t)⊗s*(-t)=h(t)⊗

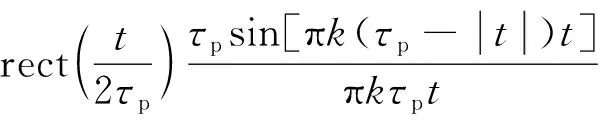
(5)

此时，主瓣的3dB带宽表示空间分辨率大小[5]，即：

(6)

式中,c表示真空中的光速，n表示光纤折射率。从(6)式可知，在TGD-OFDR系统中，空间分辨率只与扫频范围B(探测脉冲的带宽)相关，且与扫频范围B成反比，而扫频范围取决于啁啾率和脉冲宽度，可以通过增大啁啾率或者脉宽的方法提高扫频范围，实现高空间分辨率。

1.2 啁啾率、脉宽和系统信噪比的关系

在TGD-OFDR系统中，为了量化光纤感知到的外界参量的变化，必须要解调光相位，目前TGD-OFDR系统几乎都采用相干探测[13-15]方式接收光信号，并将其转换为电信号。在相干探测方法中，探测到的电信号噪声主要来自光电转换过程，主要包含：热噪声σt和散粒噪声σs两个部分。其中热噪声σt2=(4kBT/Rl)σfΔf(kB为玻尔兹曼常数，T表示绝对温度，Rl表示负载电阻，σf表示前置放大器的噪声,Δf表激光器线宽)，散粒噪声σs2=2q(I+Id)ΔB(q表示电子数目，ΔB表示带宽，Id表示暗电流，I表示电流，且Id≪I)。假设脉冲的峰值功率为Pp，则扫频脉冲信号的总能量可以表示为[5]：Ps=τpPp，信噪比(signal-to-noise ratio,SNR)可以表示为[13]：

(7)

式中，PLO表示本振信号光功率。在相干探测中，系统的散粒噪声远大于热噪声，因此热噪声可以忽略。当本振信号保持不变的情况下，信噪比主要取决于信号带宽和脉冲宽度。而ΔB=kτp，所以(7)式可以表示为：

(8)

由(8)式可知，扫频脉冲信号峰值功率与本振信号不变的情况下，系统信噪比只与啁啾率相关，且与啁啾率成反比。

1.3 啁啾率、脉宽和相位噪声的关系

系统相位噪声由系统信噪比和激光器相位噪声两个部分决定，相互之间的关系如图1所示。在相干探测系统中，随着SNR的增加，系统相位噪声先减小后保持不变[16]。而激光器相位噪声对系统相位噪声的影响相对复杂一些，散射光信号通过相干探测之后，(5)式将转化为[7]：

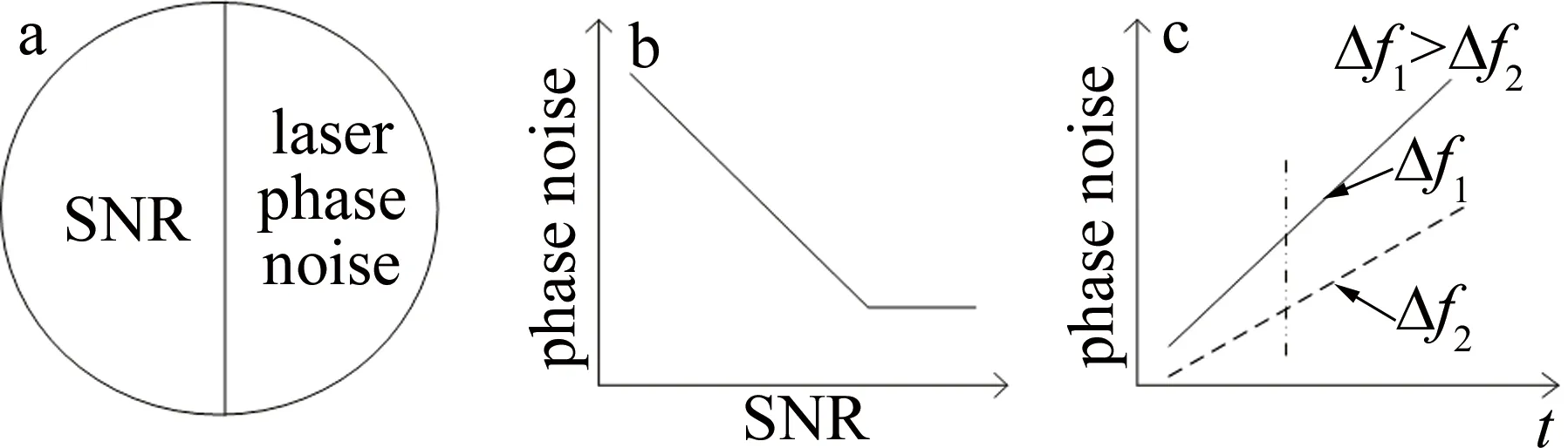
Fig.1 Factors that affect the system phase noise and their relations

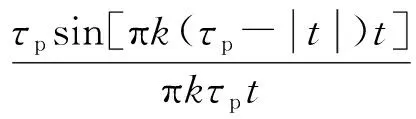
(9)

式中,Δφ(τd)=φ(t)-φ(t-τd)。其中，τd表示延迟时间，φ表示对应的相位。根据激光器相位噪声的特性可知，激光器引起的相位噪声与激光器的线宽大小相关[17-18]，通常采用标准差(standard deviation,SD)来衡量一段时间内相位噪声σφ2(t)的累积量，即：

σφ2(t)=2πΔft

(10)

由此可知，激光器相位噪声正比于激光器线宽，当激光器线宽一定时，相位噪声与t成正相关，如图1c所示。其中,Δf1,Δf2表示不同的线宽。

通过理论分析可知，当输入脉冲信号峰值功率与本振信号功率不变时，系统信噪比仅与啁啾率k相关，且与啁啾率k成反比。系统相位噪声受系统信噪比和激光器相位噪声影响。相位噪声与系统信噪比成反比，但是当信噪比达到一定阈值之后，系统相位噪声不变；当激光器线宽不变时，相位噪声与延时成正比；当扫频范围B一定时，系统相位噪声由系统信噪比和激光器相位噪声共同决定。为了验证啁啾率、信号脉宽对系统信噪比和相位噪声的影响，下面利用MATLAB对TGD-OFDR系统进行仿真。

2 仿真与结果分析

仿真时，设置起始频率f0=30MHz，传输距离为10km，采样率为1G sample/s，激光器线宽为3kHz。强度噪声通过添加高斯分布的随机数实现，激光器的相位噪声根据(10)式进行添加(文中RSNR=20lg(As/An)，As表示信号强度幅值，An表示噪声的均方根[14])。仿真过程中，本振信号功率和扫频脉冲信号峰值功率均保持不变。

验证啁啾率k与信噪比、系统相位噪声的关系时，固定的脉宽τp=5μs，初始的啁啾率k=4×1012Hz2，步长Δk=2×1012Hz2。实验结果如图2a和图2b所示。由图2a可知，啁啾率增大，SNR减小，与理论分析相符。啁啾率与相位噪声关系如图2b所示。仿真结果表明，当脉宽一定时，啁啾率与相位噪声成正相关，

Fig.2 The relation between chirp rate, pulse width, SNR and phase noise

增加速率近似于(0.0033/1013Hz2)。然后，控制啁啾率k不变，线性增大脉宽，验证脉宽与信噪比、相位噪声之间的关系。仿真时，设置啁啾率k=2×1013Hz2不变，初始的脉宽τp=1μs，步长为Δτp=0.25μs。结果如图2c和图2d所示。由图2c可知，当啁啾率k一定时，增大信号脉宽，系统信噪比基本保持不变，进一步验证系统信噪比与脉宽无关。脉宽与相位噪声的关系如图2d所示，相位噪声与脉宽τp成正相关，且其增长速率近似于(0.0025/μs)。这是由于啁啾率k不变时，系统信噪比不变，此时相位噪声的增加主要来源于激光器相位噪声。当激光器线宽固定时，脉宽增大，延时增加，导致激光器引入的相位噪声的累积量增加，系统相位噪声呈现出与脉宽成正相关的趋势。

综上所述，当输入脉冲峰值功率、本振信号功率不变时，系统SNR与啁啾率k成反比，相位噪声与脉宽、啁啾率均成正相关。由上述仿真结果可知，相位噪声随啁啾率的变化近似为0.0033/1013Hz2，脉宽对应的相位噪声增长率为0.0025/μs。由于扫频范围一定时，啁啾率与脉宽成反比，结合增长速率可知，增大脉宽，相位噪声理论上会先减小后增大，谷值大约处于12μs处(不考虑信噪比对相位噪声的影响达到最大化)。为了验证这一理论，利用MATLAB进行仿真，设置扫频范围为80MHz，起始脉宽为2μs，步长为0.5μs，仿真结果如图3所示。由图3a可知，当扫频范围B一定，增大脉宽τp，啁啾率减小，系统SNR增大。系统相位噪声总体趋势上随脉宽的增大呈现出先减小后增大的趋势，谷值处于4μs附近，与理论分析所得趋势相一致，但理论分析谷值与实际值之间存在差异可能是由于系统信噪比对相位噪声的影响达到最大化。

通过仿真分析得出，当本振信号与扫频信号峰值功率不变时，系统SNR只取决于啁啾率k，且与k成反比；扫频范围变化时，相位噪声与啁啾率和脉宽均成正相关；当扫频宽度确定时，相位噪声随脉宽的增大而先减小后增大，相位噪声存在最小值。

3 实验与结果分析

为了进一步验证啁啾率、脉宽在实际情况中对系统SNR和系统相位噪声的影响，搭建实验平台，采集实验数据进行分析处理，实验装置如图4所示。实验过程中采用3kHz线宽的激光器作为光源，通过1∶9的耦合器分为两束光:一路通过偏振控制器(polarization controller,PC)作为本振信号；另一束光通过强度调制器(intensity modulator,IM)，进行载波抑制调制。扫频信号利用任意函数发生器(artitrary function generator,AFG)产生，起始频率f0=30MHz。扫频信号通过声光调制器(acousto-optic modulator,AOM)进行脉冲调制，AOM产生的频移为200MHz，脉冲周期为Ttotal=120μs。扫频脉冲光经过掺铒光纤放大器(erbium-doped fiber amplifier,EDFA)放大后注入传感光纤中，传感光纤长度为9.5km。散射光与本振信号混合相干后接入带宽为350MHz的平衡探测器(balanced photodetector,BPD)，输出信号利用示波器采集，通过数模转换(analog-to-digital convertor,ADC)进行数据采样。采样率为1G sample/s。实验过程中控制本振光功率与脉冲光峰值功率不变。

Fig.4 Experimental setup

在验证啁啾率与信噪比、相位噪声关系时，控制初始的脉冲宽度τp=5μs不变，初始的啁啾率k=4×1012Hz2，步长Δk=2×1012Hz2。实验结果如图5a和图5b所示。实验结果表明，控制脉宽τp不变，增大啁啾率k，系统SNR减小，相位噪声增大，与仿真结果相同。

同理，验证脉宽与信噪比、相位噪声关系时，控制啁啾率不变，增大信号脉冲宽度。实验过程中设置k=2×1013Hz2，初始脉宽τp=1μs，脉宽变化Δτp=0.25μs。实验结果如图5c和图5d所示。由图5c可知，当脉宽τp增大时，系统SNR基本保持不变，即系统信噪比与脉宽无关，与理论分析、仿真结果一致。相位噪声与脉宽的关系如图5d所示。结果表明，当啁啾率不变时，信号脉宽与相位噪声成正相关，与仿真结果相符。

Fig.5 The relation between chirp rate, pulse width, SNR and phase noise

扫频范围一定时，验证脉冲参量对系统性能的影响。实验过程中设置扫频范围B=80MHz，初始脉宽τp=2μs，步长Δτp=0.5μs，由于设备限制，能够产生最大脉宽为8μs，实验结果如图6所示。其中图6a表示信噪比与脉宽的关系。由图可知，当扫频范围B一定时，系统信噪比随脉宽的增大而增加。由于扫频范

Fig.6 The relation between pulse width, SNR and phase noise when B is constant

围确定，脉宽增大，啁啾率k降低，而系统SNR与啁啾率成反比，所以，系统信噪比呈现随脉宽增加而增大趋势。相位噪声与脉宽之间的关系如图6b所示。由实验结果可知，相位噪声在2.5μs之前随脉宽的增大而减小，在2.5μs之后随脉宽的增大而增加，即相位噪声随脉宽的增加先减小后增大。实验结果与仿真结果变化趋势一致，存在差异是由于实验过程中存在外界环境波动、偏振衰落、相干衰落等情况。

4 结 论

主要研究了在TGD-OFDR系统中，扫频信号的脉宽和啁啾率变化对系统信噪比和相位噪声的影响，并进行了仿真与实验验证。结果表明，当扫频脉冲信号峰值功率与本振信号功率不变时，系统信噪比只取决于扫频信号的啁啾率，且与啁啾率成反比。在扫频范围不固定时，系统相位噪声与脉宽和啁啾率均成正相关。在实际应用中，系统中探测光的扫频范围是确定的且受探测器带宽限制，此时，增大扫频信号脉宽，系统信噪比随脉宽增大而增加，系统相位噪声随脉宽的增加呈现先减小后增大的趋势。因此，通过调节扫频信号的脉宽，可以获得最小的系统相位噪声。这一结论对系统参量设置与优化提供了思路。