Open-loop and closed-loop D α-type iterative learning control for fractional-order linear multi-agent systems with state-delays

LI Bingqiang, LAN Tianyi, ZHAO Yiyun, and LYU Shuaishuai

1. School of Automation, Northwestern Polytechnical University, Xi’an 710129, China; 2. School of Electrical and Control Engineering, Shaanxi University of Science and Technology, Xi’an 710021, China; 3. College of Electronics and Information, Hangzhou Dianzi University, Hangzhou 310018, China

Abstract: This study focuses on implementing consensus tracking using both open-loop and closed-loop Dα-type iterative learning control (ILC) schemes, for fractional-order multi-agent systems (FOMASs) with state-delays. The desired trajectory is constructed by introducing a virtual leader, and the fixed communication topology is considered and only a subset of followers can access the desired trajectory. For each control scheme,one controller is designed for one agent individually. According to the tracking error between the agent and the virtual leader,and the tracking errors between the agent and neighboring agents during the last iteration (for open-loop scheme) or the current running (for closed-loop scheme), each controller continuously corrects the last control law by a combination of communication weights in the topology to obtain the ideal control law. Through the rigorous analysis, sufficient conditions for both control schemes are established to ensure that all agents can achieve the asymptotically consistent output along the iteration axis within a finite-time interval. Sufficient numerical simulation results demonstrate the effectiveness of the control schemes,and provide some meaningful comparison results.

Keywords: multi-agent system, fractional-order, consensus control, iterative learning control, virtual leader, state-delay.

1. Introduction

In recent decades, the distributed coordination control has attracted a considerable interest in research of multi-agent systems, which has broad applications in social, industrial and national defense fields [1], such as unmanned air vehicles formation control [2,3], distributed sensor network[4], robot coordination control [5,6], attitude alignment of clusters of satellite [7,8], traffic congestion control [9,10],and so on. In multi-agent systems, the consensus control is an important problem to realize distributed coordination control. The so-called consensus problem means that the states of all agents in multi-agent systems will eventually converge through communication and coordination among the agents [11]. In the whole coordination process,the design of the distributed control law has become a crucial factor to achieve the global cooperative behavior.

Iterative learning control (ILC) has been one of the research hotspots in the control engineering field since it was proposed in 1984 [12]. In a word, it does not need the accurate mathematical model of the controlled system, but only uses the desired trajectory tracking error to correct the unsatisfactory control signals through simple iterative operation, so as to realize the tracking error to be zero in finite-time. Until now, there have been some overview descriptions, which are related to the ILC research,such as in [13,14]. On account of the simple structure,small amount of calculation and prominent tracking effect,the ILC algorithm can be used to accomplish the coordination tasks with the high precision requirement, which is carried out for multi-agent systems. In the pioneering work [15], ILC for multi-agent formation was proposed.Its purpose is to generate a control signal sequence in offline state for multi-agent formation control. Inspired by[15], an effective framework is proposed by ILC, which is for solving the formation control problem of multiple agents with unknown nonlinear dynamics. In [16], the ILC method was used to consider the finite time output consistency of multi-agent systems, and two types of distributed protocols were constructed from the perspective of two-dimensional systems. Based on [16], Meng et al.[17] gone further to achieve perfect tracking of a timevarying reference trajectory in a finite time. The objective of [18] was to hand the formation control problems for multi-agent systems. The distributed ILC algorithm was devised by using the nearest neighbor knowledge. In[19-21], adaptive ILC for consensus of multi-agent systems with non-linearity, unknown control direction and estimation of the partial derivatives were proposed respectively. In [22], a distributed mode-free adaptive ILC strategy was proposed by linearizing the dynamic characteristics of agents along the iterative axis, which realized that all agents could track the given trajectory. For multiagent systems with networked heterogeneous characteristics, each agent may have different dynamic characteristicsand different uncertainties. In [23], the convergence of iterative control was addressed, and the acceptable model uncertainty of the convergence of the proposed iterative control method was quantified. An ILC algorithm was proposed in [24], so as to solve the leader-follower formation tracking problem of a type of multi-agent system,where the expected line-of-sight range and angle profile can change iteratively, which indicates that in each iteration, the agents can have different formations.

However, in the above-mentioned researches, all are concerned with integer-order multi-agents. As is known to all, the integer-order system is one kind of the fractional-order system. In a sense, applying the fractional calculus theory to the model can depict and reflect the properties of objects more truly and precisely. The research results show that there are numerous unique advantages in the fractional-order dynamic system. In recent years, the consensus problems have been a research hotspot for many scholars who are interested in fractional-order multiagent systems (FOMASs). Through a directed interaction graph, Cao et al. [25] carried out research on distributed coordination of networked fractional-order systems. The sufficient conditions of the interaction graph and the fractional order are given to enable the general model to achieve coordination. With a view to offer a solution for consensus problems of FOMASs, Liu et al. [26] adopted the fast sliding-mode control algorithm, which was in the light of the distributed coordination theory. The communication network with a directed spanning tree will achieve an exponential finite-time consensus. For the sake of perfect tracking of the lead state, Yu et al. [27] designed and verified fractional-order observers for the fractionalorder followers where we cannot get the relative velocity information. In [28], the fractional Lyapunov direct method was applied to research FOMASs which were the common robust consensus tracking problem. These kinds of uncertain FOMASs exist a leader whose input is unknown and bounded. Consider the consensus of FOMASs by sampling data to control over the directed communication topology, which needs to satisfy 0 ＜ α ＜ 1.The necessary and sufficient conditions were established in [29]. A two-degree-of-freedom consensus scheme was investigated for FOMASs with time delay in [30]. In [31],a distributed solution with adaptive neural networks for a network was presented to realize consensus control. The single-integrator fractional-order systems belong to a class of system with nonlinear and uncertain dynamics. In[32], fractional-order singular multi-agent systems were discussed, because of the admissible leader-following consensus problem. Fractional-order singular linear systems with 0 ＜ α ＜ 2 are the basis on which the dynamics of every agent and leader are modeled. Bai et al. [33] designed a control algorithm which was based on the sliding mode estimator to hand the consensus problem for the fractional-order double-integrator multi-agent systems.Under a directed network topology, Gong [34] studied fractional-order leaderless and leader-following consensus algorithms with non-linear dynamics, using Mittag-Leffler stability and the fractional Lyapunov direct method. In view of present references, it can be seen that although there are many achievements, almost none uses the fractional-order ILC to solve the consensus problems of FOMASs, which is exactly the work to be studied in this paper.

In addition, for a specific control system, time-delay often appears not only in the state, but also in the control input or the measurement [35]. At the same time, timedelay is the fundamental reason that affects the stability and accuracy of the control system [36,37]. Strictly, the time-delay is a phenomenon that occurs in every control system, and the difference is only varying in size. Therefore, it is of great significance to do researches on the consensus control of FOMASs with time-delay. In this paper, based on the excellent performance of the ILC methodology and motivated by the search for new FOILC algorithms and their applications to fractional-order multiagent physical systems with only system state-delays,both open-loop and closed-loop Dα-type ILC laws are proposed. By means of the graph theory, norm theory and fractional calculus, we prove the convergence of the proposed control schemes theoretically, and give the sufficient conditions for convergence. Finally, the effectiveness of the proposed control schemes is demonstrated by the numerical simulation studies where we can get some meaningful comparisons between the two different control schemes.

The rest of this article is organized as follows. Some basic definitions of λ-norm, fractional calculus and graph theory are presented in Section 2. In Section 3, open-loop and closed-loop fractional-order Dα-type ILC schemes are proposed, which are designed for fractional-order linear multi-agent systems with state-delays. Moreover, the numerical simulation studies are conducted in Section 4 to validate the effectiveness of our proposed control schemes. Finally, this article is summarized in Section 5.

2. Preliminaries

For the following discussions, this section presents some mathematical definitions and lemmas.

2.1 λ-norm

We use | |·|| to define vector Euclidian norm and its induced matrix norm.

Definition 1Suppose f(·)∈C[0,T] is a continuous vector function, that is f(t)=[f1(t),f2(t),···,fn(t)]T, and its λ-norm is defined asλ ＞0[12].

2.2 Fractional calculus [38,39]

Definition 2Define the α order fractional integral of f(t) on [ t0,T] as

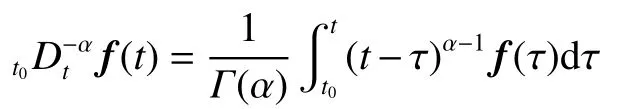
where α ＞0 , f(t) is an integrable function, Γ(·) is a Gamma function, i.e.,

Definition 3The Caputo fractional derivatives with order α can be described as

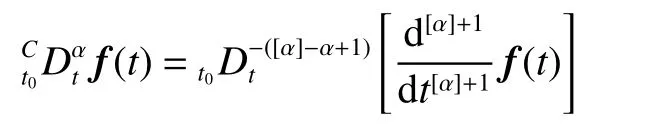
where α is a real positive constant, [ α] means rounding α,andCD means the Caputo fractional operator. To simplify the description, we use f(α)(t) to represent the Caputo derivative of f(t). The fractional-order differentiation has the following properties:

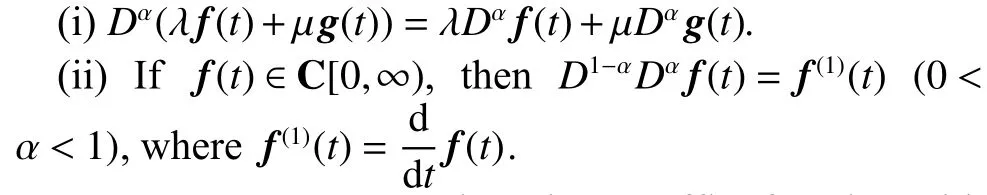
Definition 4We use the Mittag-Leffler function with α and β as

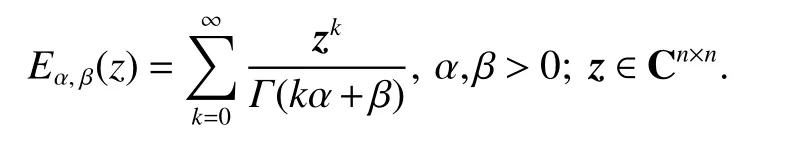
If β=1, Definition 4 with only one parameter can be expressed as

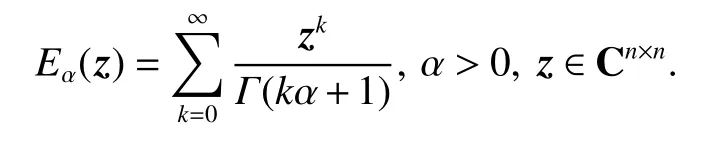
Lemma 1For the continuous function g(x(t),t), the Volterra nonlinear integral equation which is equivalent to the solution of the initial value problem

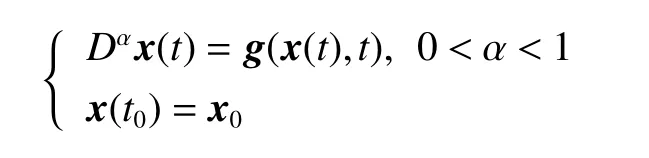
is

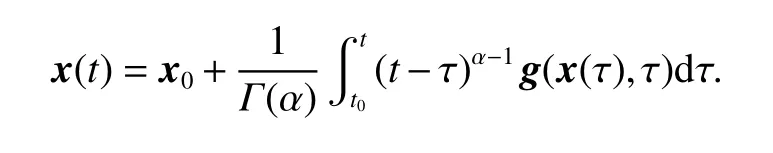
2.3 Graph theory

Consider N agents in the multi-agent systems with a directed graph G ={V,E,M}, where V ={vi} and E ⊆V×V mean the set of vertices and edges, and M means the adjacency matrix. If (i,j)∈E is defined as a direct edge between the ith agent to the jth agent, it means that the jth agent can receive information from the ith agent. Define the set of the neighbors of the ith agent as Ni={j ∈V:(j,i)∈E}, where M(G)=(ai,j)N×Nmeans the adjacency matrix of E with ai,j≥0. If (j,i)∈E and i ≠j, then ai,j=1, otherwise ai,j=0. In this paper, the communica- tion topology graph has no self-loop phenomenon, i.e.,ai,i=0[1,11].

Denote D(G)=diag{di,i=1,···,N} as the in-degree matrix, whereand we define L(G)= D(G)−M(G) as the Laplacian matrix of G. For convenience,L(G), D(G) and M(G) are abbreviated as L , D and M,respectively.

2.4 Kronecker product

Denote ⊗ as the Kronecker product, considering A, B,C and D with appropriate dimensions, the following properties can be satisfied [40]:

(i) k(A⊗B)= A⊗kB;

(ii) ( A+B)⊗C= A⊗C+B⊗C;

(iii) ( A⊗B)(C⊗D)= AC⊗BD;

(iv) | |A⊗B||=||A||·||B||.

3. Problem description

State-delay often appears in many systems which may cause instability and imprecision. Considering that a fractional-order linear multi-agent system consists ofN agents with a virtual leader, which indexes by1,2,···,N and it has the characteristics of repetitive operation in a finite time t ∈[0,T]. The dynamics of the jth agent with state-delay at the ith iteration can be described as

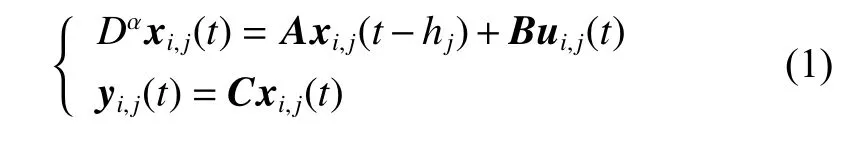
where ui,j(t)∈Rpj, yi,j(t)∈Rmand xi,j(t)∈Rqjare input,output and state, respectively, α ∈(0,1), hjmeans the jth agent’s state-delay, and hj≤T . We takewhen t ∈[−h,0], xi,j(t)=0. In (1), the exact values of coefficient matrices A and B do not need to be known.

The leader’s trajectory yd(t) is defined on a finite-time interval [ 0,T], which is generated by the leader and it can be described as follows:

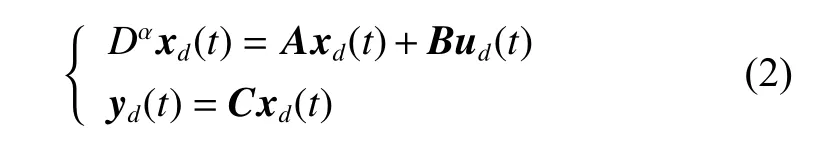
where ud(t) means the unique desired control input.

In fact, owing to communication limitations, we assume the leader’s trajectory can be accessible by a subset of the followers. Based on the graph theory, the communication graph is G ={V,E,M}. If we label the leader by vertex 0,then the complete information flow among all the agents can be characterized aswhereandare the new edge set and adjacency matrix, respectively. Thus, the purpose is to design distributed ILC schemes, which makes each individual agent in the network be able to track the leader’s trajectory under the graph

We define ξi,j(t) as the distributed information measured or received by the jth agent at the ith iteration, and it can be described as

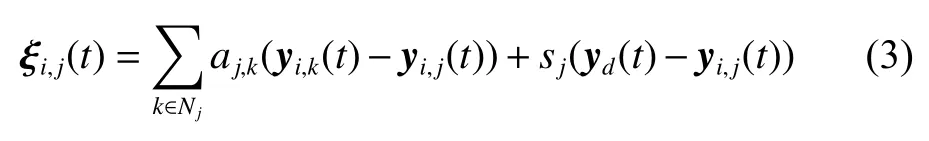
where sj=1 means the jth agent can receive the desired trajectory, i.e., (0,j)∈otherwise sj=0. The tracking error is

3.1 Open-loop Dα-type iterative learning control

For the systems (1) with state-delays, we first construct an open-loop Dα-type ILC updating law as follows:

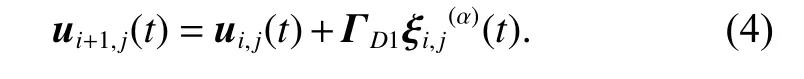
Equation (3) can be rewritten with the tracking errors as

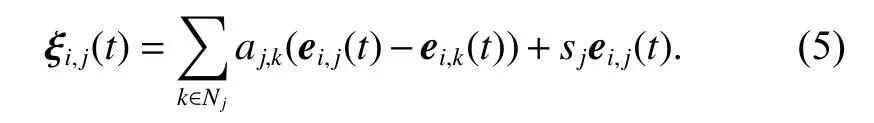
Thus, the column stack vectors in the ith iteration are defined as

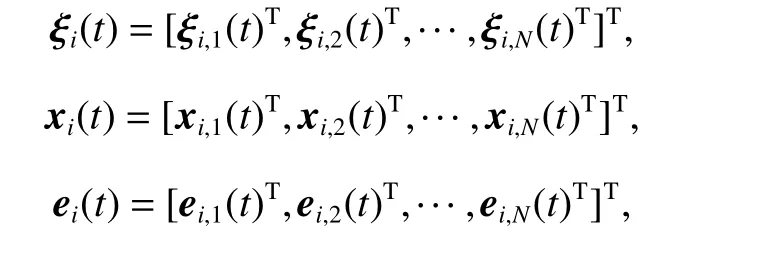
and

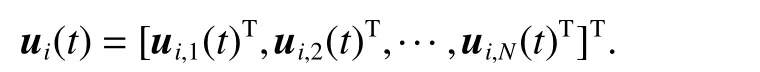
Consequently, (5) can be written as

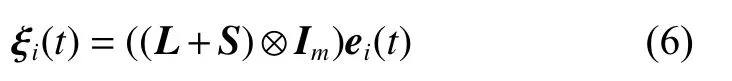
where L means the Laplacian matrix of graph G, and S=diag{sj,j=1,···,N}.

According to (6), the updating law (4) can be rewritten as

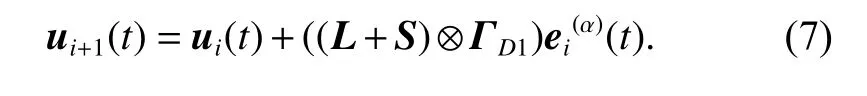
To facilitate the subsequent controller design and convergence analysis, the following three assumptions are imposed.

Assumption 1CBis of full column rank.

Remark 1Assumption 1 is a necessary condition to design a suitable learning gain such that ILC Dα-type updating law satisfies the contraction-mapping criterion.

Assumption 2The initial state of each agent in (1) is equal to the expected initial over the interval [0,T], that is, for all j , there is xi,j(0)=xd(0).

Remark 2Assumption 2 is the standard condition for ILC. If Assumption 2 is not established, the tracking performance will be degraded or control mechanisms will be required to achieve optimal tracking.

Assumption 3Considering the virtual leader being the root, the graphis a directed spanning tree.

Remark 3Assumption 3 is a necessary requirement for a leader-follower consensus tracking problem, which means that the leader is reachable for all followers. Otherwise, the isolated agents cannot track the leader’s trajectory because there is no information to correct their control inputs.

Theorem 1Consider the FOMASs (1) with statedelays and under a directed graphsuppose Assumptions 1-3 are satisfied. The controller described by (7) is applied for (1) with learning gain ΓD1, satisfying ρ1=||I −H ⊗ΓD1CB||＜1 for all t ∈[0,T], where H=L+S, thenThat is, for the achievable desired trajectories yd(t), the system outputs yi(t) converge uniformly to the desired trajectories yd(t) in t ∈[0,T] as i →∞, i.e.,

ProofDefine

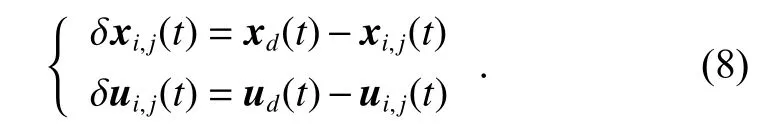
Denote δ xi(t) and δ ui(t) as the column stack vectors of δxi,j(t) and δ ui,j(t), respectively.

Obviously, if t ∈[−h,0](h ＞0), we have

According to (1), (2) and (8), we get

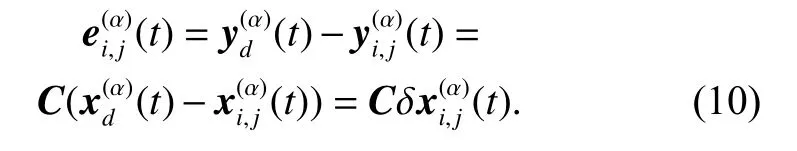
Equation (10) can be rewritten as

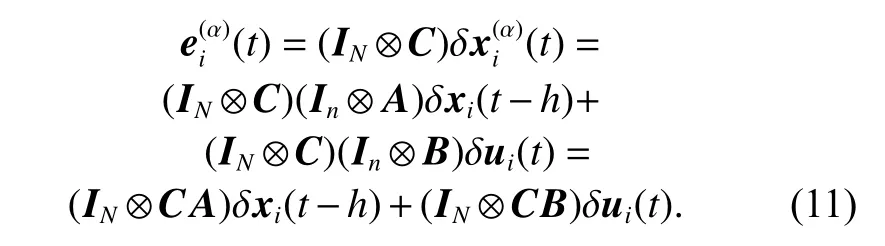
By means of Lemma 1, the dynamics of the multiagent systems (1) becomes

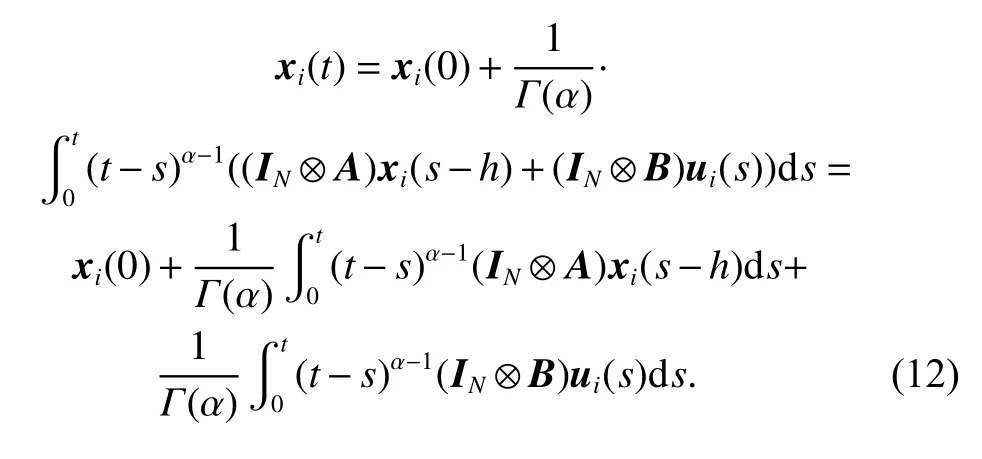
Then, from (8) and Assumption 2, we can obtain

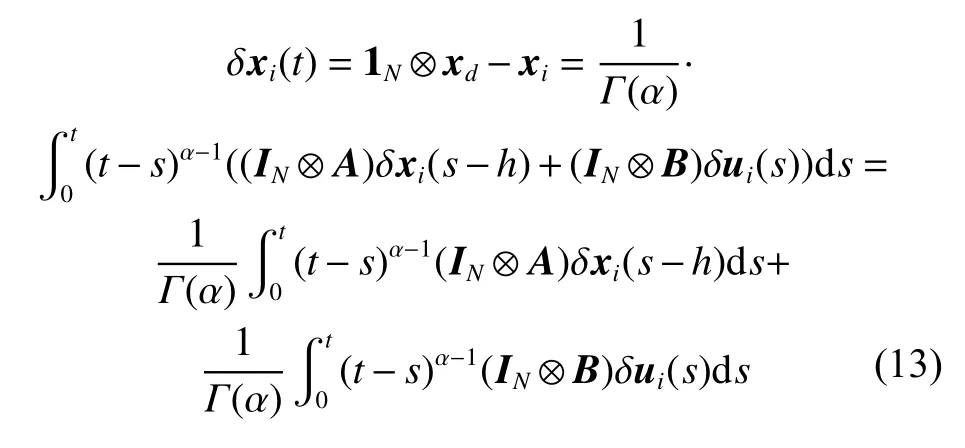
where 1(·)is a vector where all entries are 1.

Taking the norm on both sides of (13) yields

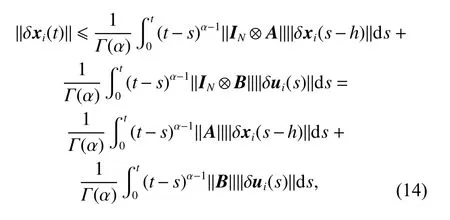
if t ∈[0,h], according (9), we can get

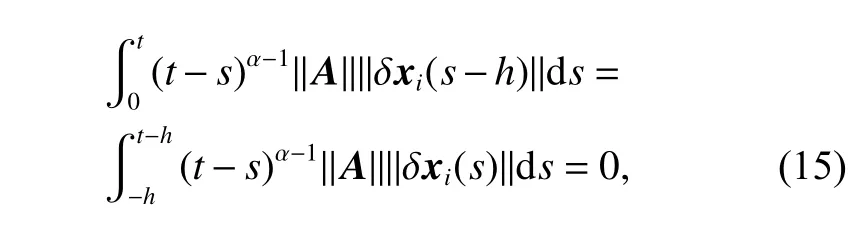
and if t ∈[h,T], we can get

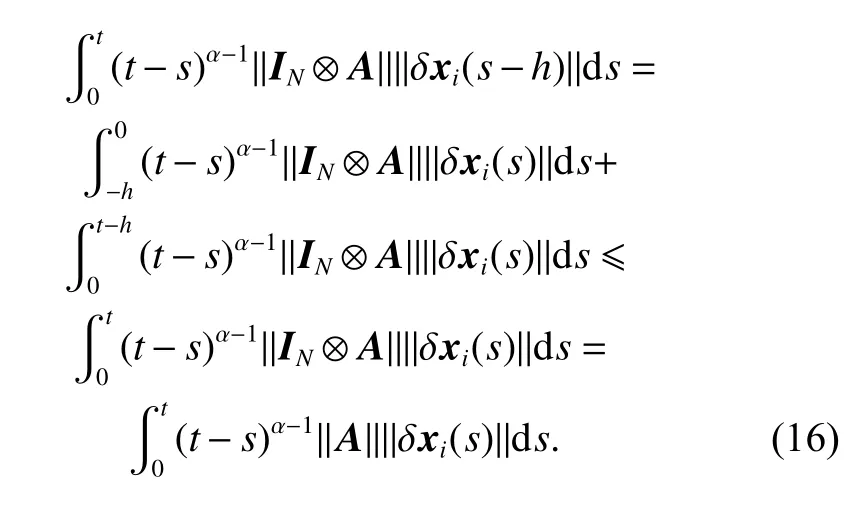
Therefore, for t ∈[0,T], combining (15) and (16) yields

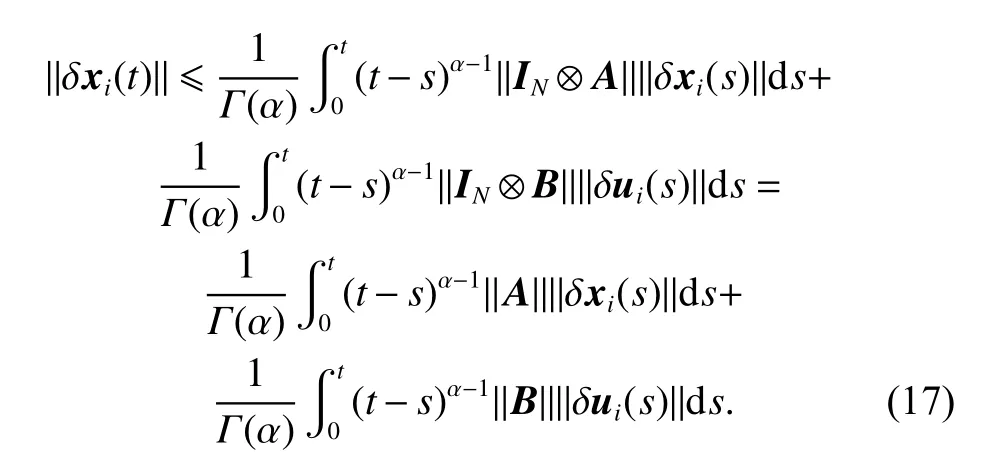
Furthermore, taking the λ-norm on both sides of (17)yields

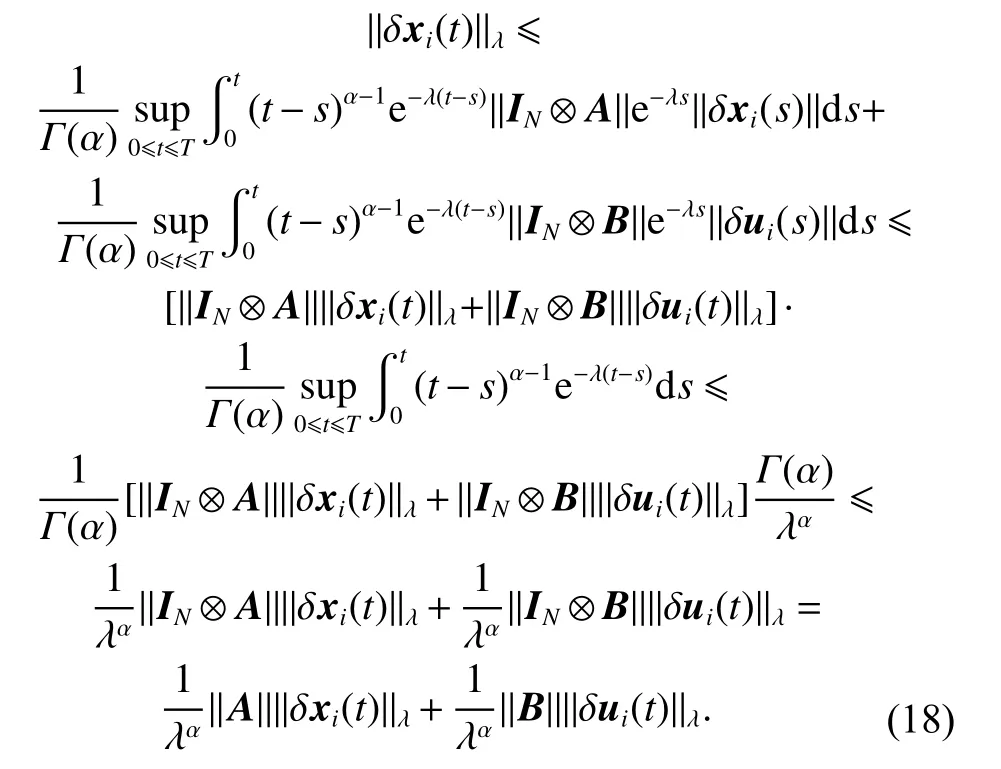
Then, if we choose a large enough value of λ to make

from (18) and (19), we can get

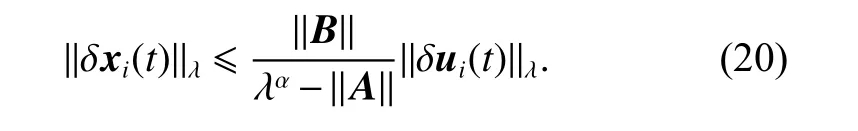
Substituting (12) and (13) into the updating law (7), we obtain

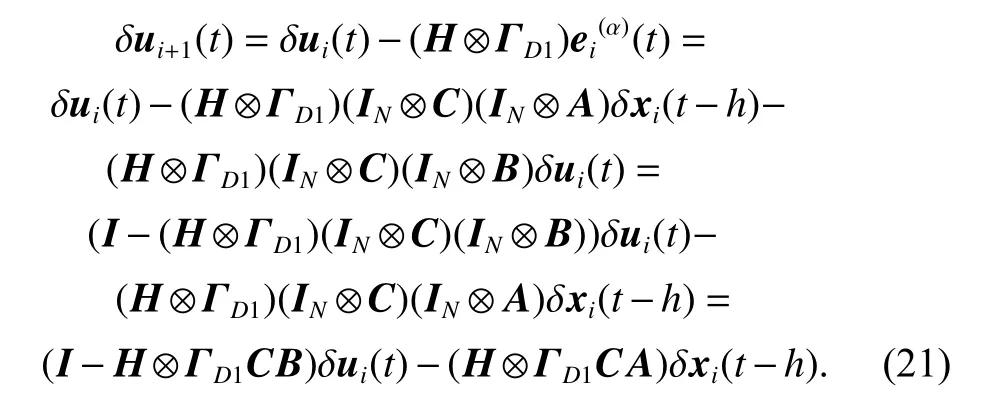
Then, taking the λ-norm on both sides of (21), we have

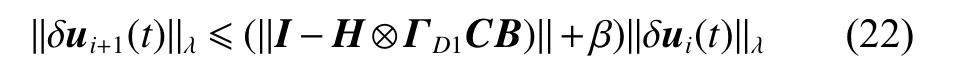
where

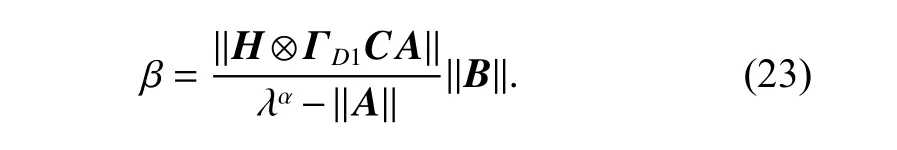
Select λ large enough to make

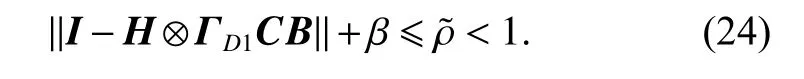
Because ρ1=||I −H ⊗ΓD1CB)||＜1, according to (22),we have

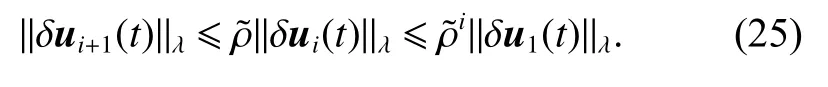
Therefore, when i →∞, we have

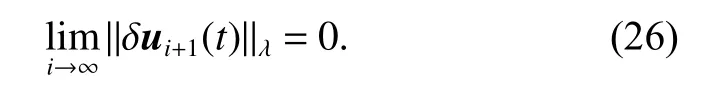
According to (20) and (26), we have

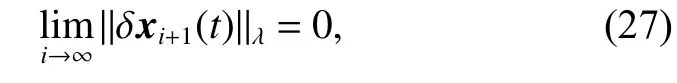
it yields

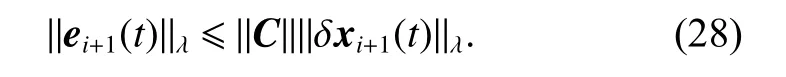
Therefore we can obtain

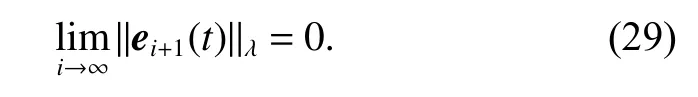
Thus, we can obtain that the tracking errors of the agents converge to zero as i →∞.

3.2 Closed-loop Dα-type iterative learning control

Now we construct a closed-loop Dα-type ILC updating law for the FOMASs (1) with state-delays as follows:

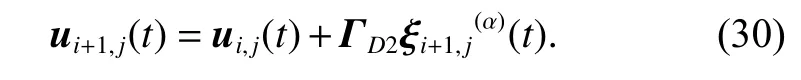
Equation (30) can be rewritten as

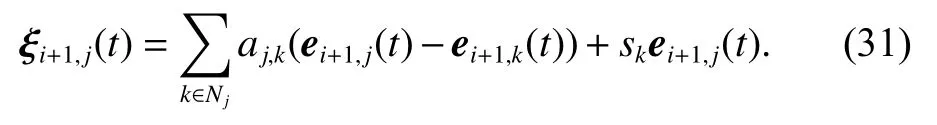
Similar to Theorem 1, (31) can be rewritten as

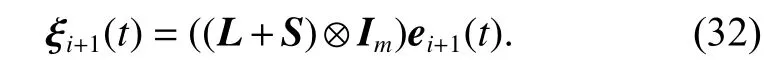
By using (32), the updating law (30) can be rewritten as

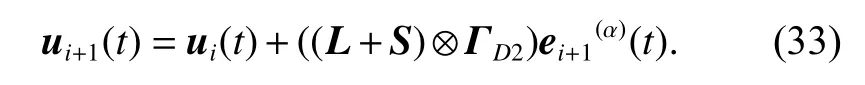
Theorem 2Consider the FOMASs (1) with statedelays and under a directed graphsuppose Assumptions 1-3 hold. The distributed closed-loop Dα-type ILC scheme (33) is applied for the system with gain ΓD2satisfyingfor all t ∈[0,T], where H=L+S , thenNamely, for the achievable desired trajectories yd(t), the system outputsyi(t)converge uniformly to the desired trajectories yd(t) in t ∈[0,T] as i →∞, i.e.,

ProofThe proof processes are similar to the proof in Theorem 1.

Considering the updating law (7) replaced by the closed-loop Dα-type updating law (30), and substituting(12) and (13) into the latter one, we can obtain

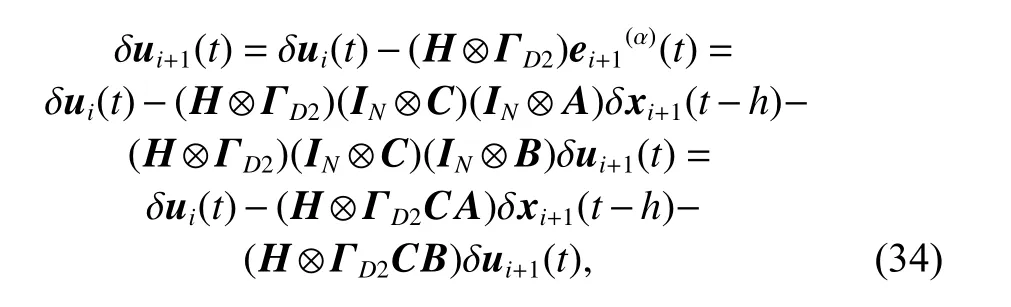
and it can be rewritten as

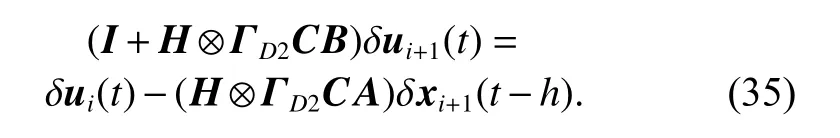
Then, taking the λ-norm of (35), and substituting (20)into it yields

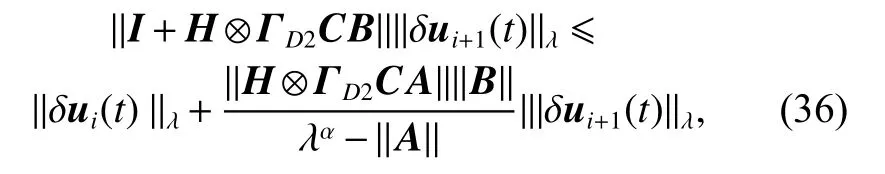
and it can be simplified as

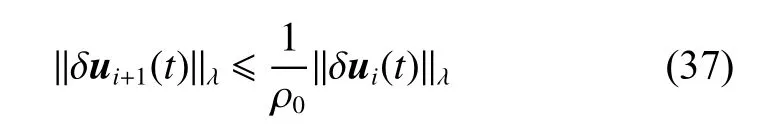
where

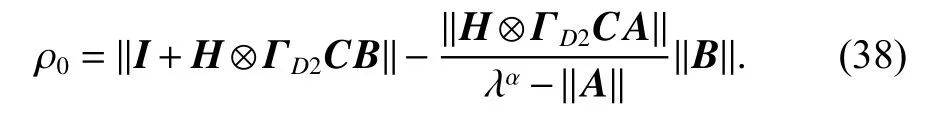
Select λ large enough to make

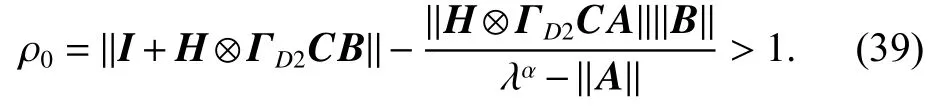
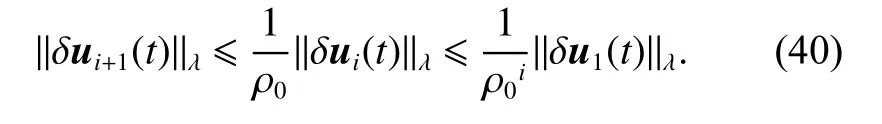
Therefore, similarly to Theorem 1, when i →∞, we can obtain

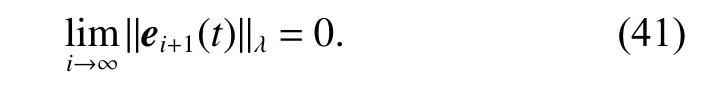
It shows that the tracking errors of the agents converge to zero as i →∞.

Remark 4In the above two proofs, the constantλ can be chosen as an arbitrary large number. Because it is just an analysis tool without using in the control process,so it does not affect the control performance.

4. Simulation

In this section, as illustrated in Fig.1, we consider a network of four agents and one virtual leader to expound the effect of the proposed consensus schemes, the virtual leader and the followers are labeled as 0, 1, 2, 3, 4, respectively. The leader has directed edges (dashed arrows)to agent 1 and agent 3. We adopt 0-1 weighting.

For Fig.1, the weighted adjacency matrix M and matrix D can be obtained as

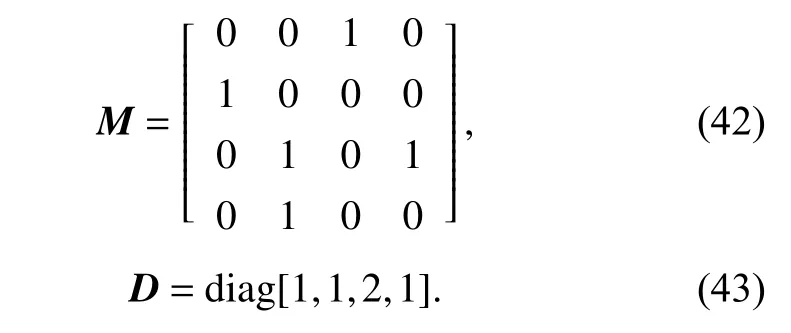
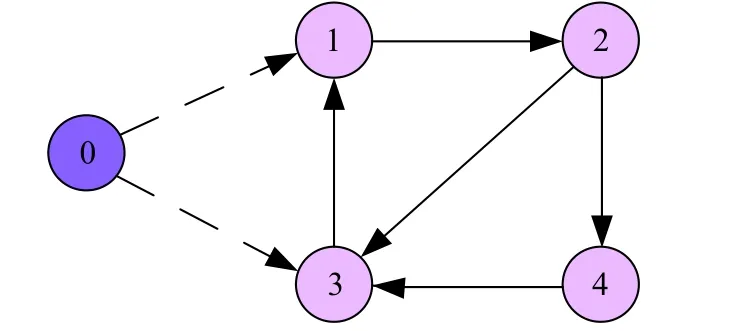
Fig. 1 Communication topology among agents

Then, the Laplacian matrix can be obtained

Consider the fractional-order dynamic model of the jth agent as

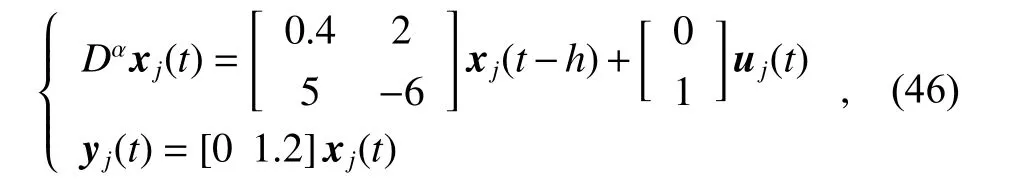
and the desired reference trajectory as

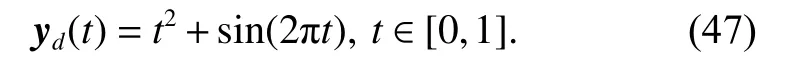
In the following examples, we set α=0.75 and designate the supremum norm as the norm of the tracking errors. For all the agents, the initial control signals at the first iteration, and the initial states for every iteration are all set as 0, that is, u0,j(t)=0 , xi,j(0)=0, j=1,2,3,4.

4.1 Open-loop Dα-type iterative learning control

Based on Theorem 1, we select the learning gain as ΓD1=0.25. Clearly, ρ1=||I −H ⊗ΓD1CB||=0.885 4 ＜1,thus the convergence condition can be satisfied.

Figs. 2-4 show the trajectory tracking performances employing the open-loop Dα-type FOILC, and the statedelays are set as h = 0.05 s, h = 0.1 s, h = 0.2 s, respectively. As it can be seen from Fig. 2(a), Fig. 3(a) and Fig. 4(a), when the state-delay becomes bigger, the tracking curves show some oscillation characteristics more and more severely at the beginning of the iterations. However,as the number of iterations increases, all the actual trajectories fit the desired trajectory very well for all the agents. By 150 iterations, the maximum tracking errors of the four agents with state-delay of h = 0.2 s are 0.002 3,0.002 4, 0.002 3, 0.002 4, respectively. Moreover, it can be seen that compared with agent 2 and agent 4, both agent 1 and agent 3 which can get information from the leader directly, can converge to the desired trajectory more quickly.

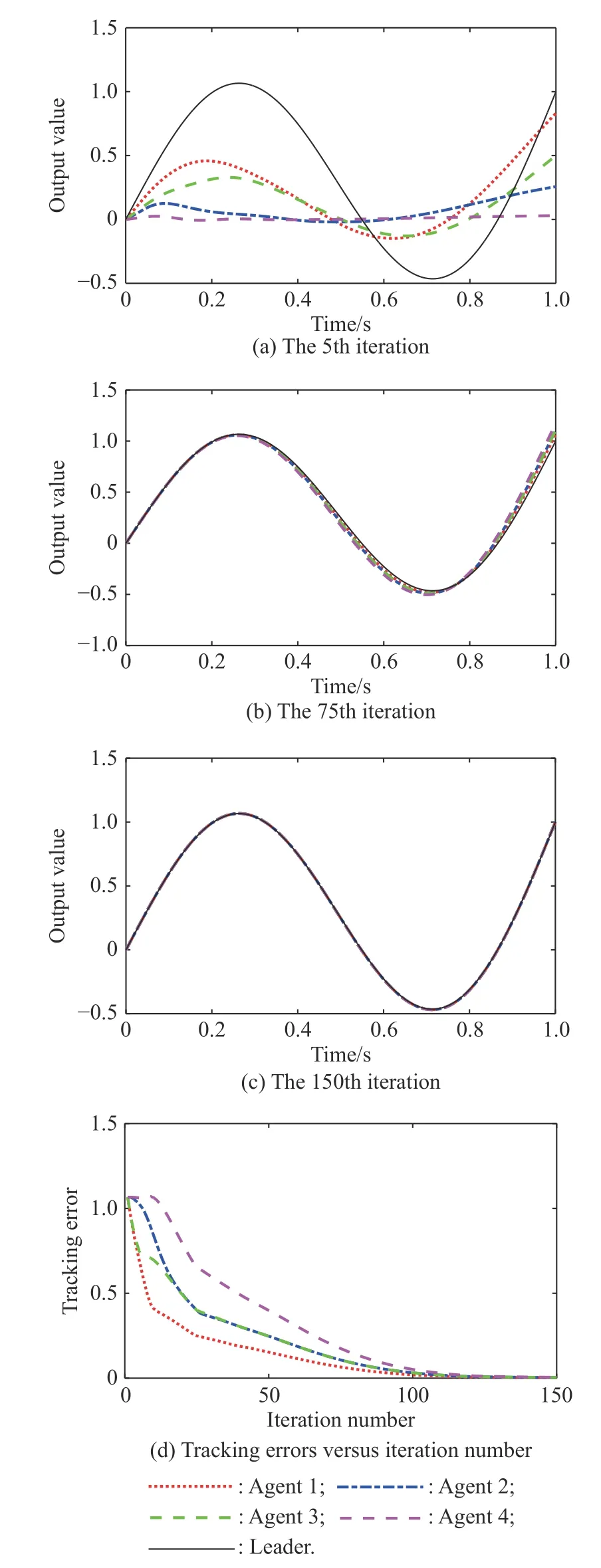
Fig. 2 Tracking performances employing open-loop Dα-type scheme (h=0.05 s)

The results show that, although in the initial several iterations, the errors will become bigger (they will become bigger with the increase of state-delays) firstly, they all can converge to infinitesimal and make the agents track the desired trajectory over the whole time interval in the presence of state-delays, verifying the effectiveness of the proposed open-loop control scheme.

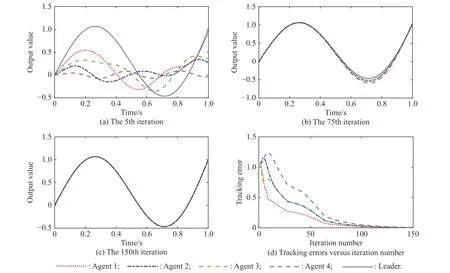
Fig. 3 Tracking performances employing open-loop Dα-type scheme (h=0.1 s)

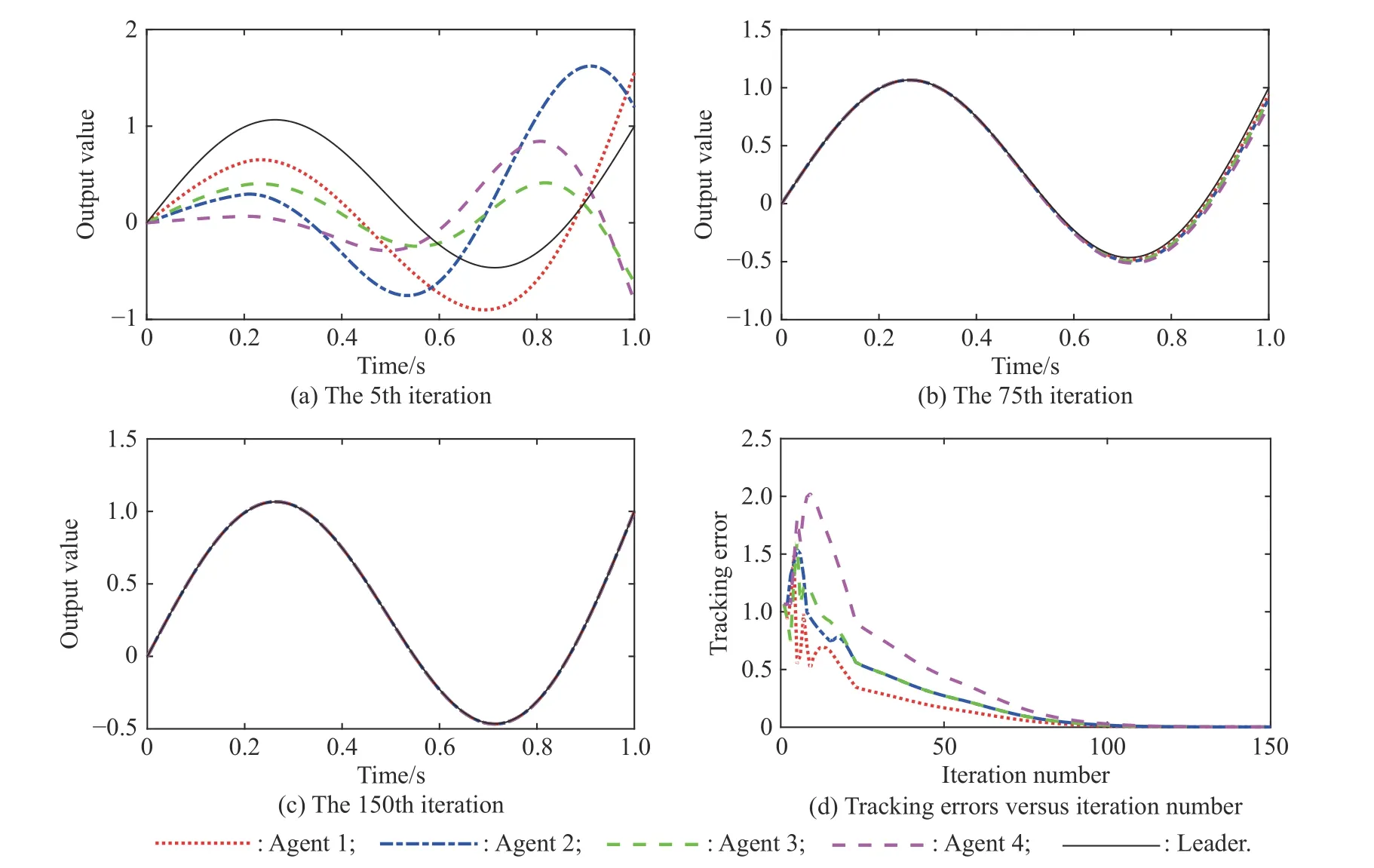
Fig. 4 Tracking performances employing open-loop Dα-type scheme (h=0.2 s)

In fact, if we select the learning gain ΓD1very small,the system will also exhibit the oscillation characteristics,and what is worse is that the convergence speed will become much slower. Therefore, it is not a good choice if we just use the open-loop Dα-type iterative learning control scheme for the consensus tracking of the FOMASs with state-delays.

4.2 Closed-loop Dα-type iterative learning control

Based on Theorem 2, we select the learning gain asΓD2=1.165. Clearly,thus the convergence condition can be satisfied.

Fig. 5, Fig. 6 and Fig. 7 show the trajectory tracking performances employing the closed-loop Dα-type iterative learning control scheme, and the state-delays are also set as h = 0.05 s, h = 0.1 s, h = 0.2 s, respectively. As it can be seen from Fig. 5(a), Fig. 6(a) and Fig. 7(a), when the state-delay becomes bigger, the tracking curves will not show the oscillation characteristics which appear in the open-loop Dα-type iterative learning control scheme.From Fig. 5(d), Fig. 6(d) and Fig. 7(d), it can be observed that the closed-loop Dα-type iterative learning control scheme can make the agents track the desired trajectory monotonously over the whole time interval in the presence of state-delays. By only 50 iterations, the maximum tracking errors of the four agents with state-delay of h = 0.2 s are 0.000 9, 0.001 3, 0.001 1, 0.001 5, respectively, yet already less than that of the open-loop scheme by 150 iterations. Therefore, the proposed closed-loop scheme can obtain much better tracking performance and robustness in the presence of state-delays, verifying the effectiveness of the proposed closed-loop control scheme.Moreover, just like the results exhibited in the open-loop control scheme, it can also be seen that both agent 1 and agent 3 can converge to the desired trajectory more quickly than agent 2 and agent 4.

In fact, as it can be seen from Theorem 2, we can select the learning gain ΓD2large enough, so that the system will converge more quickly and still with no oscillations, which has been verified by detailed simulation but not presented here due to limited space. Therefore, the closed-loop Dα-type ILC scheme performance is superior to the open-loop one in the speed of convergence and robustness for the consensus tracking of the FOMASs with state-delays.

Remark 5Actually, many real physical systems exhibit fractional-order dynamic characteristics, but the integer-order calculus theory which is always used is just a special case of the fractional-order calculus theory and it can only describe the actual fractional-order system approximately. However, the fractional calculus theory can depict and reflect the properties of objects more truly and precisely, and with fractional-order controller, the system can obtain a better performance. Therefore, it is of great significance for the results we get in this paper.

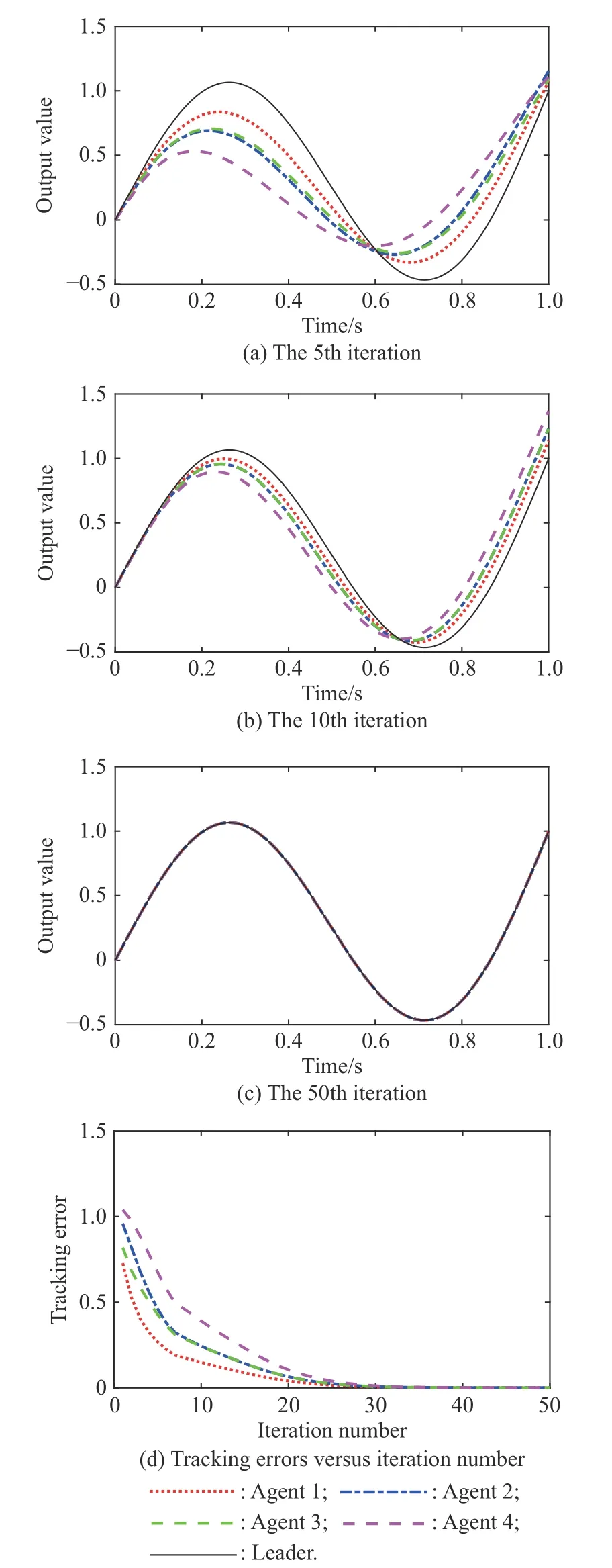
Fig. 5 Tracking performances employing closed-loop Dα-type scheme (h=0.05 s)

Remark 6In fact, the open-loop and the closed-loop Dα-type iterative learning control are feedforward and feedback control techniques, respectively. Compared with the former one, the closed-loop Dα-type iterative learning control can use the real-time feedback information so as to stabilize the control system, and it can also choose a large enough learning gain which can make the convergence more quick.

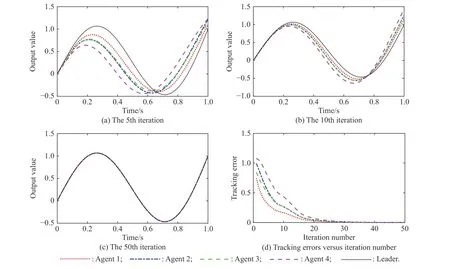
Fig. 6 Tracking performances employing closed-loop Dα-type scheme (h=0.1 s)

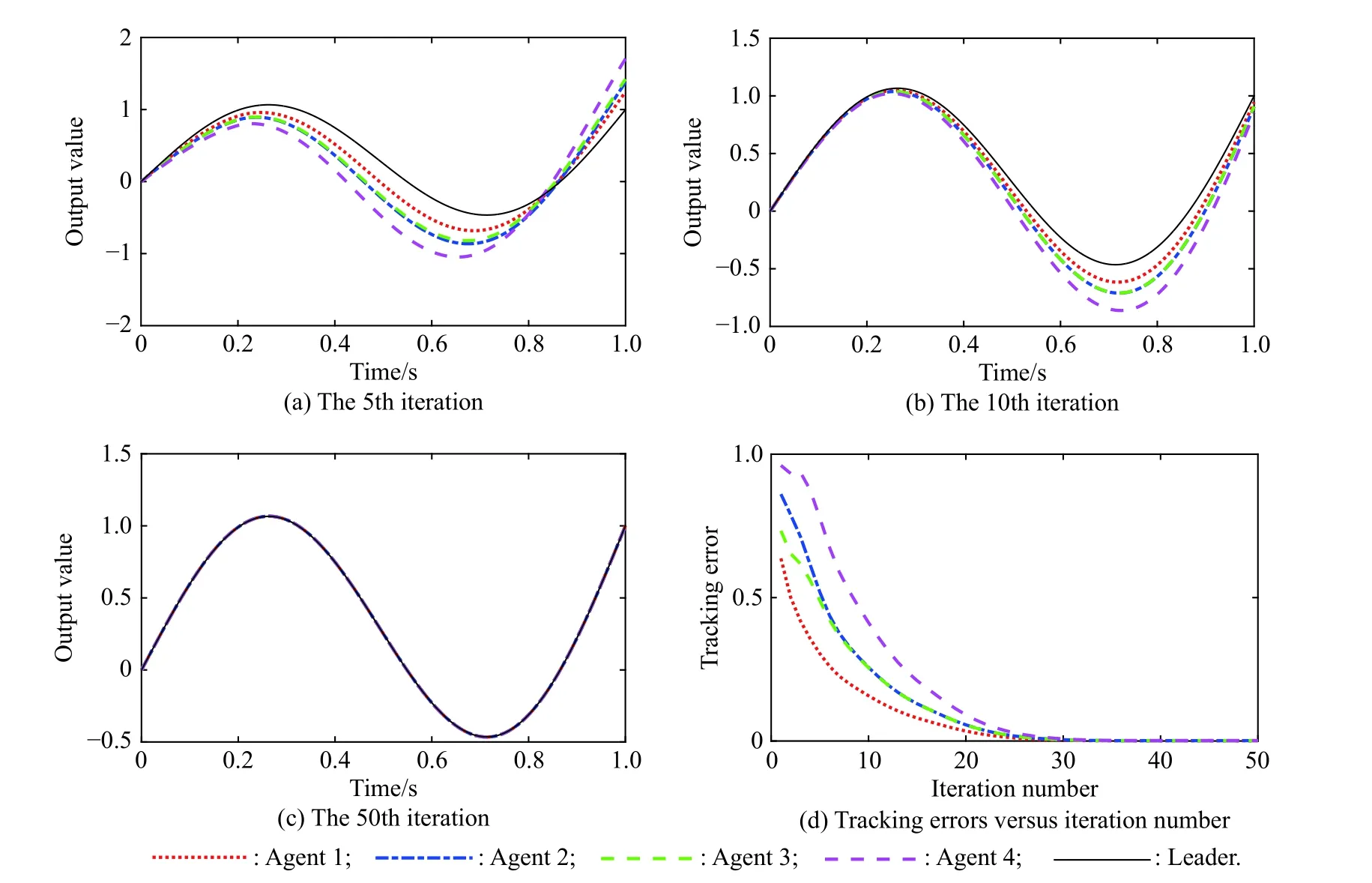
Fig. 7 Tracking performances employing closed-loop Dα-type scheme (h=0.2 s)

Remark 7We can combine the open-loop and closedloop Dα-type iterative learning control together to achieve open-closed-loop Dα-type iterative learning control, which can utilize both the previous and current operation information of the FOMASs simultaneously, so that its performance will be better than that of the simple single open-loop or closed-loop iterative learning control.

5. Conclusions

This paper consider the problem of consensus tracking for fractional-order linear multi-agent systems. These systems have the same characteristics of state delays and under a repeatable operation environment. Both open-loop and closed-loop Dα-type iterative learning control schemes are proposed to perform the consensus tracking.

The convergence to the desired trajectory is strictly analyzed, and sufficient conditions are obtained. Theoretical analysis and numerical simulation show that even if only a subset of the followers can get information from the leader, either of the agents can track the desired trajectory over the entire time interval with state-delays, using both two control algorithms. By comparison, it is found that the closed-loop scheme has a better performance in terms of convergence speed and robustness in the case of state-delays. Furthermore, we can be able to do research on the open-loop and closed-loop PDα-type iterative learning control schemes for the fractional-order linear or the nonlinear multi-agent systems with statedelays or the control-delays. We further verify the effectiveness of the algorithm through experimental verification.