Higher order implicit CNDG-PML algorithm for left-handed materials

CHEN Yanfang and WANG Liwei

1. School of Electrical and Information Engineering, Tianjin University, Tianjin 300072, China;2. Tianjin Key Laboratory of Intelligent Information Processing in Remote Sensing, Tianjin Zhongwei Aerospace Data System Technology Co., Ltd., Tianjin 300450, China

Abstract: By incorporating the higher order concept, the piecewise linear recursive convolution (PLRC) method and Crank-Nicolson Douglas-Gunn (CNDG) algorithm, the unconditionally stable complex frequency shifted nearly perfectly matched layer(CFS-NPML) is proposed to terminate the left-handed material(LHM) domain. The proposed scheme takes advantages of CFSNPML formulation, the higher order concept PLRC method and the unconditionally stable CNDG algorithm in terms of absorbing performance, computational efficiency, calculation accuracy and convenient implementation. A numerical example is carried out to demonstrate the effectiveness and efficiency of the proposed scheme. The results indicate that the proposed scheme can not only have considerable absorbing performance but also maintain the unconditional stability of the algorithm with the enlargement of time steps.

Keywords: complex frequency shifted nearly perfectly matched layer (CFS-NPML), Crank-Nicolson Douglas-Gunn (CNDG), lefthanded material (LHM), piecewise linear recursive convolution(PLRC).

1. Introduction

The left-handed material (LHM) has excited public ’s interest due to its unique characteristic on simultaneously negative permittivity and permeability in a certain frequency band [1,2]. However, the LHM cannot be obtained directly from nature. Thus, LHM simulation is regarded as the most important way to entirely research its behaviors in a series of situations [3]. As one of the most powerful and efficient numerical simulation tools, the finite-difference time-domain (FDTD) algorithm, proposed by Yee, has received considerable attention not only in solving the Maxwell’s equations but also in simulating practical electromagnetic problems, especially the wave propagation in the dispersive LHMs [4,5]. It is known that the conventional FDTD algorithm is a time explicit algorithm. That means the time step and the mesh size are limited by the Courant-Friedrichs-Lewy (CFL) condition [6]. If the CFL condition cannot be satisfied, the conventional FDTD algorithm will be unstable. This characteristic limits the application of the conventional FDTD algorithm. Especially in the multi-scale problems and calculation of fine structures, large amount of time steps must be calculated resulting in much more expensive simulation which becomes unacceptable in the practical engineering. To enhance the computational efficiency and shorten the CPU time, a series of unconditionally stable algorithms are investigated. Among them, it has been testified that the Crank-Nicolson (CN) scheme can receive better efficiency and accuracy during the simulation[7,8]. Although the original CN scheme is efficient in onedimensional case, large sparse matrices will be formed by directly applying the original CN scheme to two-dimensional cases. So far, the calculation method in solving the sparse matrices shows quite low efficiency. To avoid the calculation of such large sparse matrices, the approximate CN algorithms are proposed in two-dimensional cases including the CN approximate-decoupling (AD)and the CN Douglas-Gunn (DG) algorithms [7,8]. It has been testified that the CNDG can obtain better accuracy by introducing the disturbances terms at both sides of the equations compared with the CNAD algorithm [9].

By applying the CNDG algorithm to open region problems, infinite rows of data must be calculated by computer in theory [6]. It is obvious that such procedure is unpractical to realize. To simulate the infinite extension of computational domain, the absorbing boundary condition must be introduced during the simulation. The perfectly matched layer (PML), proposed by Berenger, is regarded as one of the most powerful absorbing boundary conditions [10]. The original PML is implemented by splitfield scheme resulting in the employment of six auxiliary variables. To improve the computational efficiency and simplify the implementation at corners and edges of the PML regions, the stretched coordinate PML formulation with four auxiliary variables is proposed [11]. However,the updated equations must be changed according to different domains. Thus, the nearly PML (NPML) based on stretched coordinate (SC) variable is introduced [12].Both the SC-PML and the original NPML are inefficient in reducing late-time reflections and attenuating evanescent waves. To alleviate such problems, the complex frequency-shifted (CFS) PML is carried out [13]. Through the resultants, it can be founded that the reflection coefficient in the low-frequency is relatively low. The reason is that the low-frequency propagation waves cannot be efficiently absorbed. The high order PML formulation is introduced to alleviate such question and enhance the absorbing performance during the whole simulation [14]. The original higher order PML is implemented with six auxiliary variables, which affects the accuracy and efficiency[15]. Recently, the improved PML algorithm with four auxiliary variables is introduced based on different implementations [16,17].

So far, the higher order CNDG-PML is introduced based on the auxiliary differential equations method [9].By applying the proposed scheme to the LHMs, the implementation will become much more complex to be realized. In addition, the PML for LHMs are mainly based on the conventional CFS-PML and the CNAD algorithms[18-20]. The accuracy of the LHM algorithm still needs to be improved.

Here, based on the higher order PML scheme, the CNDG algorithm and the CFS-NPML formulation, the unconditionally stable CNDG higher order CFS-NPML is proposed, denoted as CNDG-HO-NPML, in the LHM computational domain. The frequency-dependent LHM is simulated by the PLRC method in terms of considerable accuracy and efficiency. A numerical example is introduced to investigate the effectiveness and efficiency. The resultants indicate that the proposed scheme takes advantages of the higher order PML concept, the CNDG algorithm and the CFS-NPML formulation in terms of considerable efficiency, simplifies implementation and outcome absorbing performance when the time step surpasses far beyond the CFL condition compared with the previous works.

2. Method and formulation

In the higher order NPML regions for LHMs in 2-D transverse magnetic (TM) case, the Maxwell’s equations can be given as the following forms:

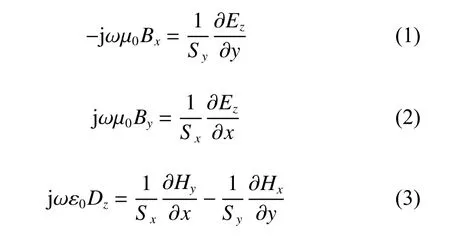
where

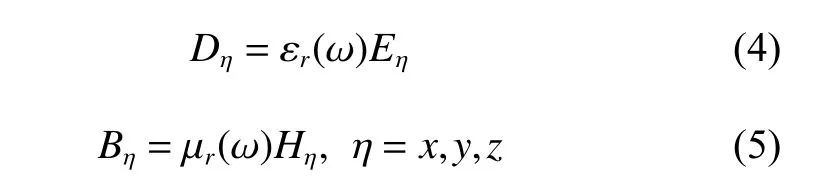
where εr(ω) and µr(ω) are the permittivity and permeability of the frequency-dependent LHM, respectively[19,20]. In the common LHMs, the permittivity and permeability are assumed to be identical. For the frequencydependent LHM, the constitutive relationship can be expressed by the Drude model as

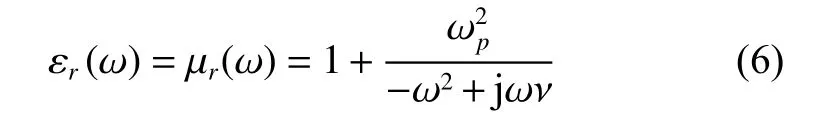
where ωpis the plasma frequency and ν is the damping constant [21]. Within the higher order NPML regions, the stretched coordinate variables with the CFS factor can be given as

where κηn≥1 is real and σηn, αηn(n=1,2) are assumed to be positive real. By employing the partial fraction method,can be given as

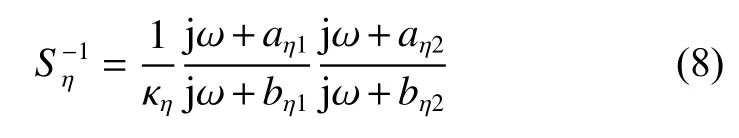
where the coefficients can be given asBy substituting (8) into (1)-(3),employing the relationshipand introducing the auxiliary variables, the equations can be rewritten as the following forms:

where the auxiliary variables can be given as

where the coefficients are

and the operator denotes the CN scheme, expressed as

where the coefficients can be given as

The updated equations of auxiliary variables can be given as

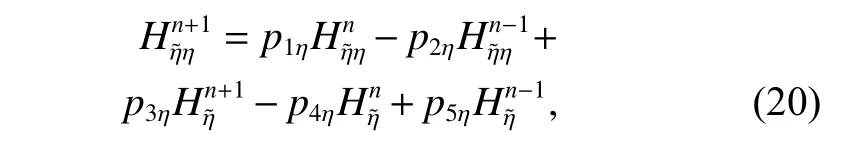
where the coefficients are

By substituting (19) and (20) into (14)-(16), one obtains

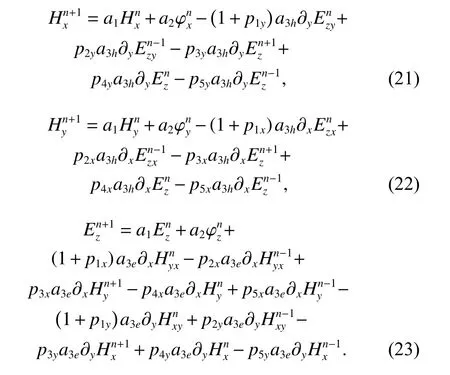
By substituting (21) and (22) into (23), the equation can be written as

By introducing the operator D2η=a3ea3hp3η∂η∂η, (24)can be given as

where

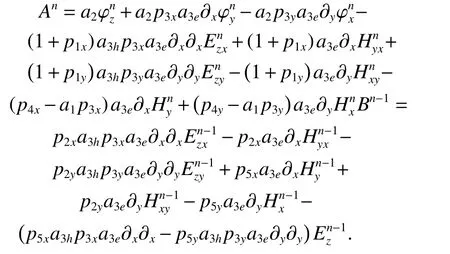
According to the CNDG scheme,andare added at both sides of (25), the equation can be given as

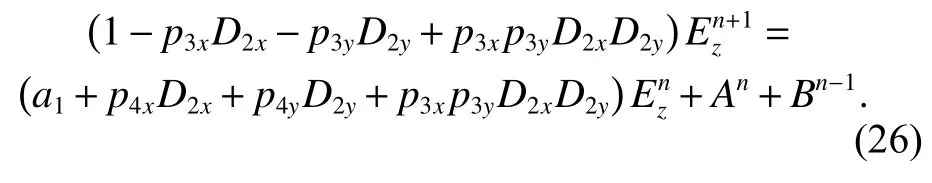
Equation (26) can be updated by two sub-split procedures as follows:

It can be observed that Ezcomponent can be updated by calculating two tri-diagonal matrices. Onceis calculated, the other components can be updated explicitly.

3. Numerical validation and results demonstration

To demonstrate the efficiency and performance of the proposed implementation, a numerical example is carried out in the 2-D FDTD computational domain. As shown in Fig. 1, a ridge waveguide model which is composed of partial filled LHM and vacuum is employed during the simulation.

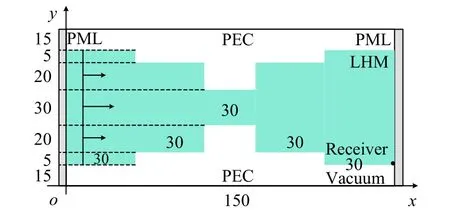
Fig. 1 Sketch picture of LHM ridge waveguide structure

The computational domain has dimensions of150∆x×110∆y. Inside the waveguide structure, the ridge can be regarded as the combination of five rectangles with the dimensions of 30∆x×80∆y, 30∆x×70∆y, 30∆x×30∆y,30∆x×70∆y and 30∆x×80∆y. The LHM is filled inside the rectangle with the parameters of ωp=3×109rad/s and ν=9×107Hz. The rest part of the structure is filled with vacuum. At the left of waveguide structure, a plane Gaussian pulse source which has the maximum frequency of 30 GHz is incident along the positive side of x-direction. The distance between the source and the left boundary is 10 cells. At the right bottom corner of LHM, the receiver is employed to observe the propagation waveform and evaluate the reflection of PML regions. At the top and bottom of the structure, the perfectly E conductor(PEC) is employed. At the right and left of the structure,the computational domain is terminated by 8-cell-PML.

Inside the PML regions, the parameters are chosen to obtain the best absorbing performance both in the time domain and the frequency domain. For comparison, the CNDG based CFS-PML (CNDG-PML) in [20], CNAD based HO-PML (CNAD-HO-PML) in [19], conventional FDTD based HO-PML (FDTD-HO-PML) in [17] and conventional FDTD based CFS-PML (FDTD-PML) in[22] are chosen for the further demonstration of effectiveness and efficiency. The parameters of CNDG-HO-NPML,CNAD-HO-PML and FDTD-HO-PML are chosen as αη1=1.2 , mη1=2 , κη1=260 , ση1=1.8ση1_opt, αη2=0.6 ,mη2=2, κη2=1 and ση2=0.05ση2_opt, where σηn_optcan be given as

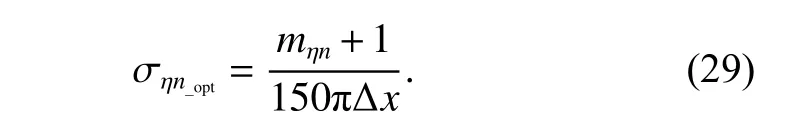
For CNDG-PML and FDTD-PML, the parameters can be chosen as αη=1.0 , mη=3, κη=280 and ση=1.7ση_opt.

To demonstrate the effectiveness of the proposed algorithms and make comparison between different PML algorithms, cell per wavelength (CPW) is chosen as 200.The mesh size can be chosen as ∆x=∆y=∆=50 μm.The time step can be calculated by=0.12 fs,whereis the maximum time step which satisfies the CFL limit in the conventional FDTD algorithm. In the unconditionally stable algorithms, the CFL number (CFLN)is defined as

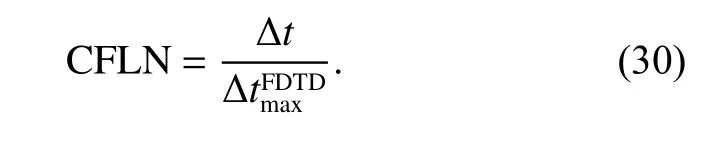
To evaluate the absorbing performance in the time domain, the relative reflection error is employed during the implementation which can be defined as

Fig. 2 shows the relative reflection error versus time during the simulation time of 1.2 ns with different CFLNs obtained by different PML algorithms. The maximum relative reflection error (MRRE) is considered for the further evaluation during the simulation.

Fig. 2 Relative reflection error versus time during the simulation time of 1.2 ns

The MRRE obtained by FDTD-PML, CNDG-, FDTDHO-, CNAD-HO-PMLs CFLN=1, CNDG-HO-NPML CFLN=1, CNDG-, CNAD-HO-PMLs CFLN=10, CNDGHO-NPML CFLN=10 are -50 dB, -58 dB, -85 dB,-78 dB, -82 dB, -41 dB, -75 dB and -80 dB, respectively. It can be concluded that the proposed CNDG-HONPML can receive better performance during the whole simulation duration. Compared with FDTD-PML and CNDG-PML, the proposed scheme can improve the absorbing performance during the whole simulation and reduce the MRRE of the PML algorithm. Compared with CNAD-HO-PML, it can be observed that the MRRE can be decreased as well indicating the effectiveness of the proposed PML scheme. The reason is that the CNDGFDTD algorithm can decrease the numerical dispersion resulting in the higher accuracy and better performance compared with the CNAD-FDTD scheme. Meanwhile, it can be observed that the absorbing performance of the proposed scheme is inferior compared with the FDTDHO-PML. The consumption memory, MRRE, CPU time and time reduction obtained by different PML algorithms with different CFLNs are shown in Table 1.

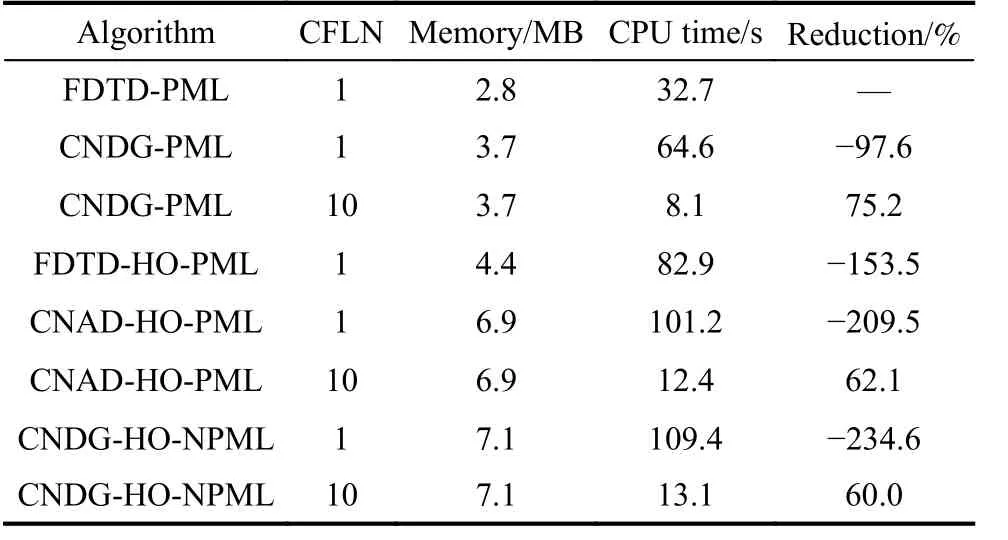
Table 1 Time of different algorithms

It can be concluded that the CNAD and the CNDG algorithms consume much CPU time and memory compared with the FDTD-PML and the FDTD-HO-PML. The reason is that tri-diagonal matrices must be solved at each time step during the simulation process resulting in such phenomenon. The CPU time can be significantly reduced by employing larger CFLNs. When CFLN=10, the CPU time decreases by 75.2%, 62.1% and 60.0% compared with FDTD-PML, respectively. The proposed scheme and the CNAD-HO-PML occupy the similar resources. Furthermore, the efficiency can be enhanced.

The absorbing performance can also be evaluated by the reflection coefficient in the frequency domain, defined as

where FFT{·} is the Fourier transform. Fig. 3 shows the reflection coefficient versus frequency with different PML algorithms and the normalized incident pulse spectrum of the source.

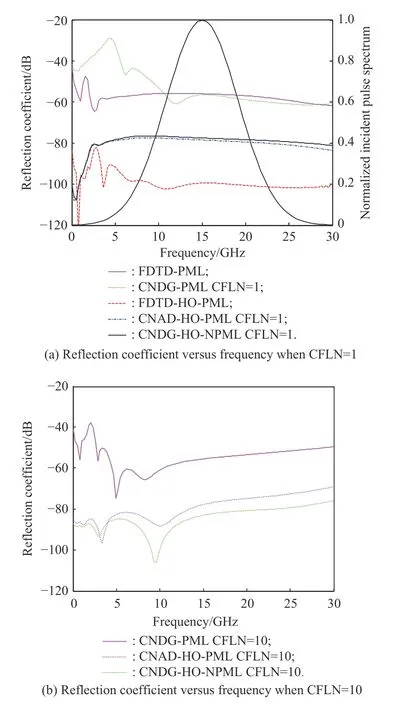
Fig. 3 Reflection coefficient versus frequency

It can be observed that the reflection coefficient can be decreased by employing the HO-PMLs during the whole interesting frequency band. Meanwhile, the reflection coefficient decreases significantly at the low-frequency indicating that the low-frequency propagation waves can be absorbed by employing the proposed scheme.

4. Conclusions

By incorporating the CNDG algorithm, the HO-PML scheme and CFS-NPML formulation, the unconditionally stable CNDG-HO-NPML is proposed for LHM simulation. Numerical example is carried out to demonstrate the effectiveness and efficiency. Through the resultants, it can be concluded that the proposed scheme takes advantages of HO-PML, CNDG-FDTD and CFS-NPML in terms of considerable absorbing performance and favorable computational efficiency when the time step surpasses far beyond the CFL limit.