STAP method based on atomic norm minimization with array amplitude-phase error calibration

PANG Xiaojiao, ZHAO Yongbo, CAO Chenghu, XU Baoqing, and HU Yili

National Lab of Radar Signal Processing, Department of Electrical Engineering, Xidian University, Xi’an 710071, China

Abstract: In this paper, a space-time adaptive processing(STAP) method is proposed for the airborne radar with the array amplitude-phase error considered, which is based on atomic norm minimization (ANM). In the conventional ANM-based STAP method, the influence of the array amplitude-phase error is not considered and restrained, which inevitably causes performance deterioration. To solve this problem, the array amplitude-phase error is firstly estimated. Then, by pre-estimating the array amplitude-phase error information, a modified ANM model is built, in which the array amplitude-phase error factor is separated from the clutter response and the clutter covariance matrix (CCM) to improve the estimation accuracy of the CCM. To prove that the atomic norm theory is applicable in the presence of the array amplitude-phase error, the clutter sparsity is analyzed in this paper. Meanwhile, simulation results demonstrate that the proposed method is superior to the state-of-the-art STAP method.Moreover, the measured data is used to verify the effectiveness of the proposed method.

Keywords: atomic norm minimization (ANM), space-time adaptive processing (STAP), airborne radar, array amplitude-phase error.

1. Introduction

Recently, space-time adaptive processing (STAP) technologies have attracted significant attention because of its potential to improve the detection performance of the moving targets in strong clutter environment for airborne radar application [1-3]. Due to the motion of the radar platform, one-dimensional processing in neither Doppler nor angle domain can detect the moving targets in the clutter background. Therefore, it is necessary to perform the joint angle-Doppler processing. Brennan and Reed firstly proposed the fully STAP method with joint angle-Doppler processing [3]. It is vital that the clutter covariance matrix (CCM) is effectively estimated in STAP methods, which is used to design the STAP filter to maximize the output signal-to-clutter ratio (SCR). Due to the lack of the prior knowledge about clutter, a large number of independent and identically distributed (IID) training samples are needed to estimate the CCM. Nevertheless, a lot of IID training samples are unavailable since the clutter is non-stationary and heterogeneous in the practical environment. Thus, the fully STAP method is impractical because of its large computational complexity and a large number of sample requirements. Thus, the partially adaptive STAP approaches with approximate optimum performance are developed to reduce the computational burden and training support [4-7].

To reduce the number of training samples and maintain the clutter suppression performance, many related algorithms have been proposed over the last decades. The reduced-dimension (RD) methods project the space-time data vector onto a lower dimensional subspace through linear transformation to reduce the number of the required training samples [4-6]. Motivated by the low rank nature of clutter, the reduced-rank (RR) methods transform the clutter response into a lower dimension data through the transformation matrix, which is dependent of the clutter data [7]. However, the training samples required by the RD and RR methods can hardly be obtained in nonstationary scenarios. The direct data domain (D3) STAP method proposed in [8] can bypass the problem of lacking training data support by utilizing the data of the range cell under test (CUT). Unfortunately, since the D3 method only exploits partial statistical information, the degree of freedom (DOF) is decreased, which causes a great loss of clutter suppression performance. Moreover, the D3 method suffers from computational burden. Since the prior knowledge is not exploited for estimating the CCM, the convergence rate can hardly be improved. For the knowledge-aided STAP (KA-STAP) methods developed in[9-11], both the prior knowledge and data observations are utilized to obtain instantaneous characteristics of the CUT. However, the accuracy of the prior knowledge directly affects the performance of these methods. It means that how to make full use of the prior knowledge is still a crucial problem.

Since the convergence rate of the statistical STAP methods is slow and the KA-STAP methods are sensitive to the prior knowledge, the sparsity-based STAP methods have been extensively researched [12-18]. Motivated by the intrinsic sparsity of clutter and advanced reconstruction algorithms, the sparsity-based STAP methods can construct the clutter plus noise covariance matrix (CNCM)accurately with a small number of training samples [19].However, the clutter mitigation performance of the sparsity-based STAP methods is unstable because the corresponding sparsity-based space-time filter is sensitive to the regularization parameter, clutter degrees of sparsity, and noise power. Thus, the sparsity-based methods have been modified in the different ways. In [19], to improve the reconstruction accuracy of the sparse representation recovery (SR), the multiple measurement vectors(MMV) model and the sparse Bayesian learning (SBL)strategy have been applied. Since the SBL is independent of the prior parameters, the robust estimation of the sparse spectrum can be ensured in an uncertain environment. In addition, several methods have been proposed to reduce the computational complexity of the sparsitybased STAP methods, such as the fast-converged sparse Bayesian learning method [20], beamspace post-Doppler dimension reduced sparsity-based STAP method [21],and a STAP method with sparse constraint based on conjugate gradient techniques [22].

However, existing sparsity-based methods are presented in the discrete domain. Since the space-time vectors of the clutter subspace cannot be exactly expressed, the off-grid or mismatch problem occurs, which inevitably causes clutter suppression performance degradation [23].To solve this problem, a series of novel gridless compressed sensing (CS)-based STAP methods are developed to estimate the CCM via atomic norm minimization (ANM) [24-26]. However, nearly all the ANMbased STAP methods employ ideal signal models without considering the array amplitude-phase error. The sparsitybased STAP methods in [27,28] were proposed, which considered the array amplitude-phase error. However, the signal model of this method is built by discretizing the angle-Doppler plane, whose performance will be degraded due to the off-grid problem.

In this paper, an ANM-based STAP method considering the array amplitude-phase error is proposed. The rank and the sparsity of the CCM in the presence of the array amplitude-phase error are firstly analyzed, which is the primary condition for the application of the atomic norm theory to the CCM estimation. Then, the array amplitudephase error is estimated through the single auxiliary source algorithm. After that, the positive semidefinite(PSD), block-Toeplitz, and low rank properties of the CCM with the array amplitude-phase error are exploited.Based on the error estimation information pre-estimated,a modified ANM model is established, in which the array amplitude-phase error factor is separated. Since the array amplitude-phase error is calibrated, the proposed method can obtain more accurate estimation of the CCM and better clutter suppression performance compared to the existing ANM-based STAP method. Finally, simulation results validate the performance of the proposed method.The main contributions of this paper can be summarized as follows.

(i) The sparsity of clutter with the array amplitudephase error is analyzed.

(ii) The array amplitude-phase error is isolated to reduce its influence on the CCM estimation. Based on the error estimation information, a modified ANM model is established to estimate the CCM.

(iii) The measured data is used to verify the correctness and effectiveness of the proposed method.

The remainder of this paper is organized as follows.The signal model for airborne radar with the array amplitude-phase error existing is introduced in Section 2. In Section 3, the rank of the CCM and the clutter sparsity with the array amplitude-phase error are analyzed. Then the proposed ANM-based STAP with the array amplitudephase error calibrated method is illustrated in detail. After that Section 4 provides simulation results to verify the performance of the proposed method. Finally, Section 5 summarizes this paper.

2. Signal model

Consider a side-looking airborne radar with a uniform linear array (ULA) which consists of M elements with inner spacing d. Each antenna transmits a coherent burst of Npulses in a coherent processing interval (CPI) with the constant pulse repetition frequency (PRF) fr. The platform is at an attitude haand flies with a constant moving velocity v. Suppose that the clutter return is modeled as a large number Ncof independent clutter patches which are uniformly distributed in azimuth angles. Range ambiguity and jamming signals are ignored for simplicity. In this paper, the amplitude-phase error, modeled asτ=[τ1,···,τm,···,τM]Tis considered, where [·]Tdenotes the transpose operator. In the presence of the array amplitudephase error, the received clutter-plus-noise signal of the lth target-free range cell can be expressed as

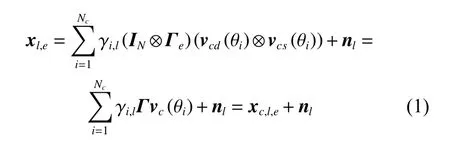
where Γe=diag(τ) and Γ=IN⊗Γe. diag [·] denotes the trace operator, INis an N×N unit matrix, xc,l,edenotes the clutter response with the array amplitude-phase error of the l th range cell, γi,lis the random amplitude of the ith clutter patch of the lth range cell, ⊗ represents the Kronecker product, vcd(θi) and vcs(θi) respectively represent the temporal steering vector and the spatial steering vector, which are given by

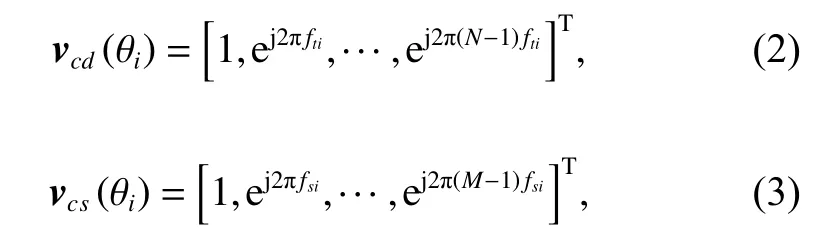
where j is an imaginary unit, fsiand ftiare respectively the spatial frequency and the normalized Doppler frequency of the ith clutter patch. fsiand ftican be cast as

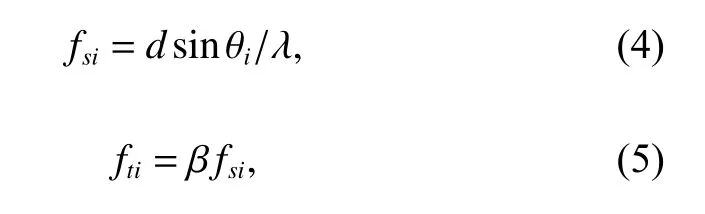
where β=2v/(d fr) is the clutter ridge slope and λ is the wavelength. Meanwhile, the space-time steering vector of the ith clutter patch is vc(θi)=vcd(θi)⊗vcs(θi) . nldenotes the thermal noise, which follows zero-mean Gaussian distribution with covariance matrix σ2INK. σ2represents the noise power. Considering that the clutter patches are mutually independent, the CNCM can be written as

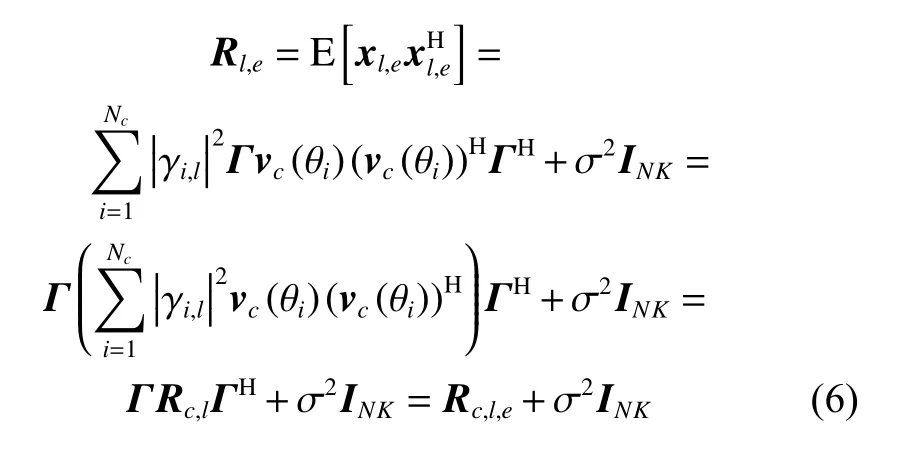
where [·]His conjugate transpose operation, E[·] denotes the expectation,and Rc,l,eare both estimated by single training samples, Rc,lrepresents the CCM without the array amplitude-phase error, and Rc,l,erepresents the CCM with the array amplitude-phase error.

If multiple training samples are supported, the clutterplus-noise signal matrix of L training samples considering the array amplitude-phase error can be expressed as

where E denotes the thermal noise matrix. The corresponding average CNCM is calculated as

where Rcrepresents the average CCM without the array amplitude-phase error, and Rc,erepresents average CCM considering the array amplitude-phase error.

3. The proposed method

3.1 Analysis of sparsity and rank of CCM with array amplitude-phase error

In [12], the sparsity of the clutter is analyzed, while only ideal cases without any error are considered. In this subsection, the rank and the sparsity of the clutter with the array amplitude-phase error is analyzed. According to the Brennan ’s rule [1], for a side-looking ULA with the fixed PRF, constant velocity, no crab, and without the array amplitude-phase error, the rank of the CCM can be given by

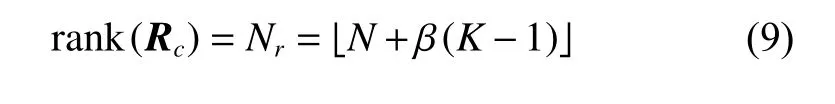
where Nris the rank of the clutter estimated by the Brennan rule and the bracketindicates rounding to the nearest integer. As rank(AB)=min(rank(A),rank(B)),the rank of the CNCM Rc,eis equal to

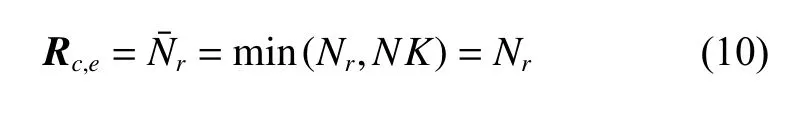
Proposition 1For a side-looking ULA with the fixed PRF, constant velocity, no crab and without amplitudephase error, the clutter subspace can be approximately represented by the subspace obtained by a set of uncorrelated space-time steering vectorswhich can be expressed as

where

The proof of Proposition 1 is given in [12]. Based on Proposition 1, the clutter response without the amplitudephase error can be rewritten as

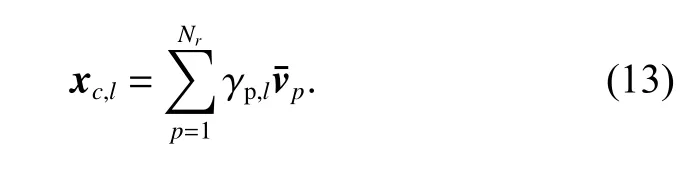
The relationship between xc,l,eand xc,lis as follows:

Since multiplying xc,lby Γ does not change the sparsity of clutter response xc,l, xc,l,eis sparse. Thus the clutter response with the amplitude-phase error can be expressed as

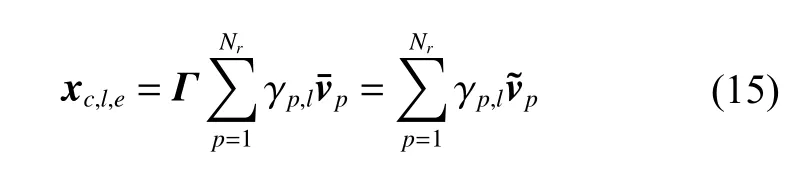
From the above analysis, the clutter sparsity is equivalent to the rank of the CCM.

3.2 ANM method

The conventional STAP method based on the atomic norm mainly focuses on the ideal model without considering the array amplitude-phase error. The conventional method can be divided into two steps. The first step is estimating the clutter covariance matrix. Then the STAP filter weight vector is designed. In this section, the ANMbased STAP with the array amplitude-phase error considered is proposed.

It is motivated by [24] that the performance of the reconstruction can be improved when the multiple training samples are alternative. Thus, the proposed method mainly discusses the multiple training samples. The clutter signal matrix of L training samples can be expressed as

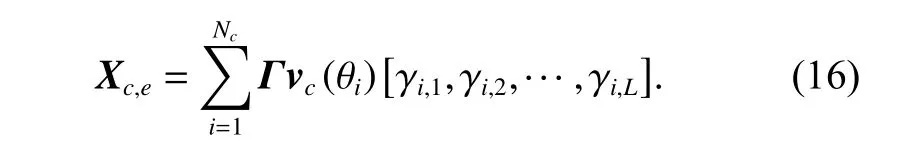
According to the clutter sparsity in (15), (17) can be expressed as

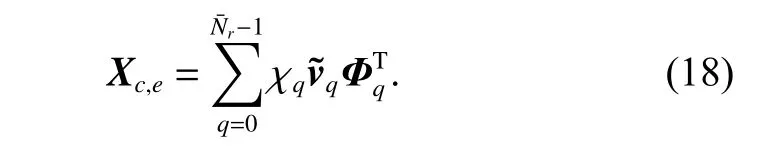
It can be found from (18) that Xc,ecan be seen as a linear combination ofatoms in the atomic set AMMV,which is defined as

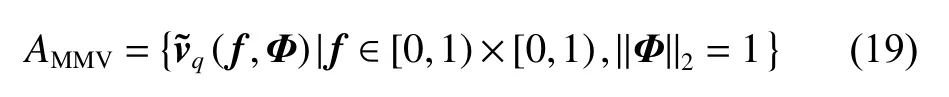
The recovery of clutter information can be achieved by solving the following ANM optimization problem:

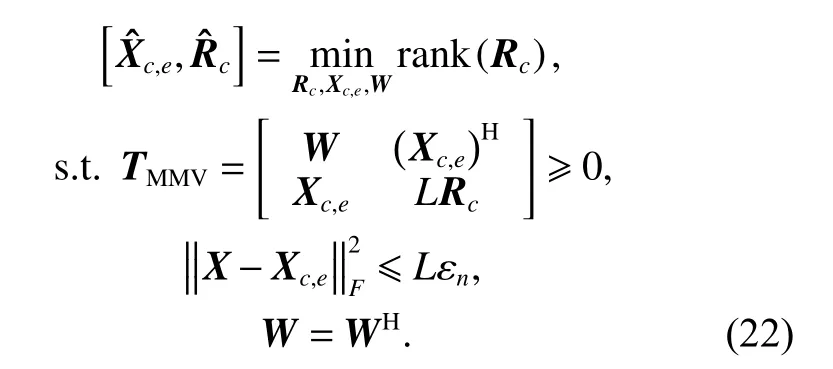
ProofLet

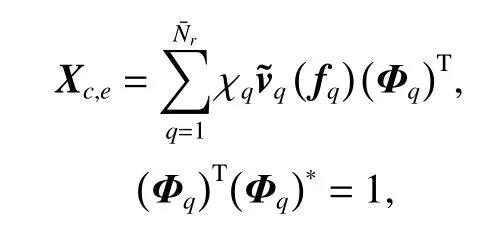
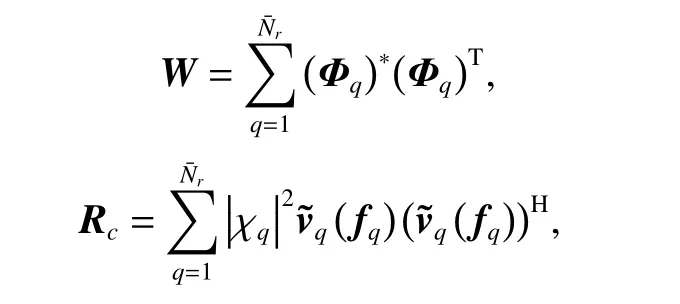
then TMMVcan be formulated as

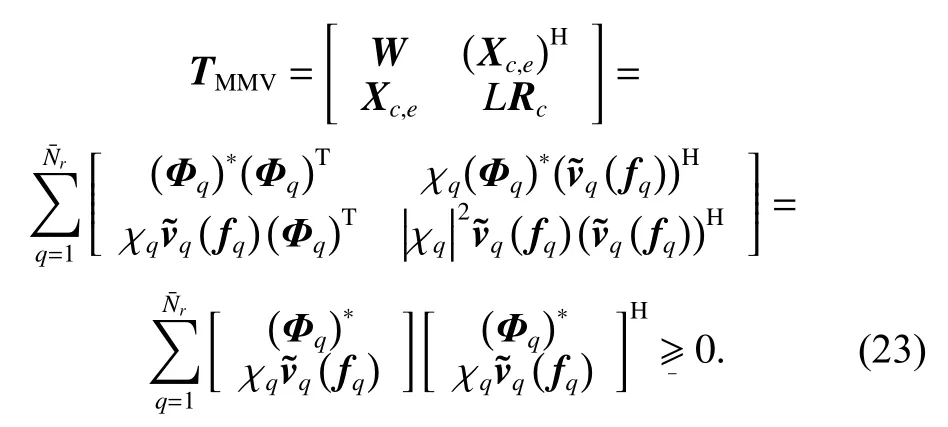
Thus, rank(TMMV)=rank(Rc). It can be proved that(21) equals (22). □

Although the rank minimization problem is NP-hard, it is proved that (22) can be solved by trace relaxation [29].Meanwhile, the PSD block-Toeplitz property of Rcis utilized, (22) can be reformulated as

where trace[·] denotes the trace operator, U is a complex matrix with size (2N −1)×(2K −1), and S(U) is a twofold block Toeplitz matrix using the same method in [30].Generally speaking, the solution Rcof (24) is considered to be the CCM. However, the semi-definite matrix TMMVcan be decomposed into many forms which satisfy the constrains of (24). For example, it can be derived that

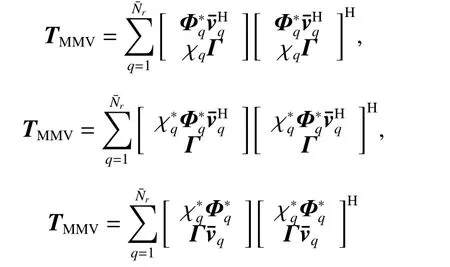
and

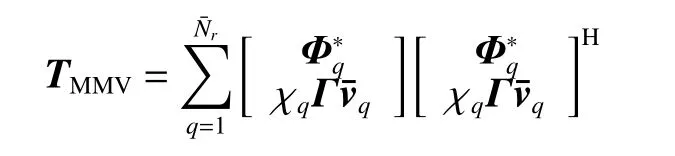
satisfy the constrains of (24), which means that the solution Rcof (24) is not unique. Therefore,estimated by(24) is not the accurate CCM estimation.

As a matter of fact, unknown variables Xc,eand Rcin(24) include another unknown variable Γ. In order to solve unknown variables Xc,e, Rc, and Γ of (24), the amplitude-phase error matrix Γ is first estimated through the single auxiliary calibration algorithm [9]. The single auxiliary calibration algorithm utilizes the irrelevance of noise and signals, and calculates the array amplitudephase error through the received signal, which is emitted by a known azimuth auxiliary source [9]. Then, the clutter information and the CCM are obtained by solving the following minimization problem:

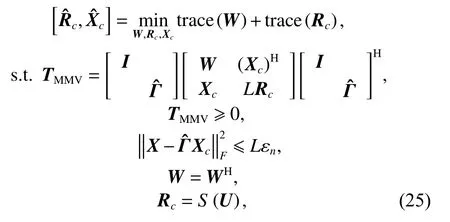
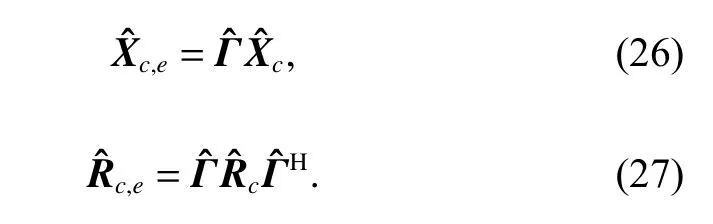
However,

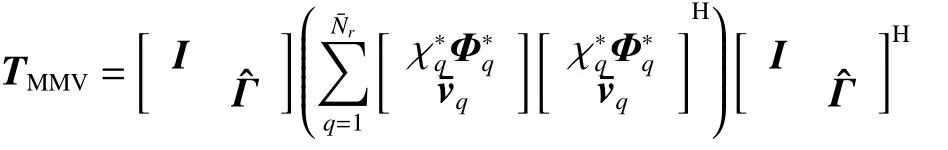
and

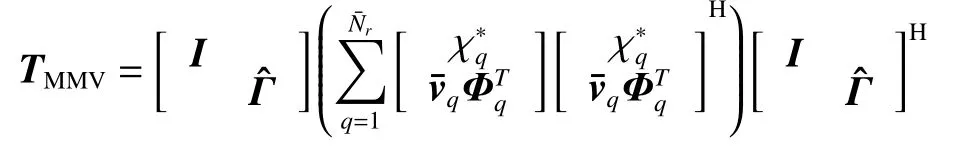
both satisfy the constrain of (25). Thus, the CCM estimation is not accurate.

In order toobtain more accurate CCM, the matrixis decomposed [25] as

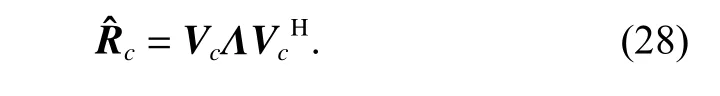
Then the CCM can be expressed as

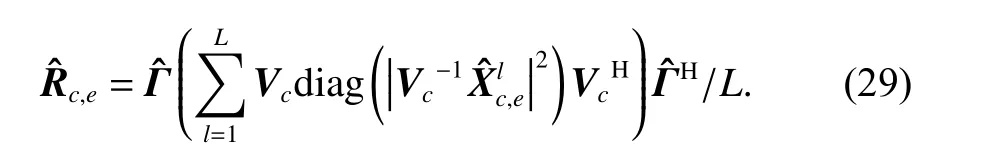
The CNCM can be expressed as

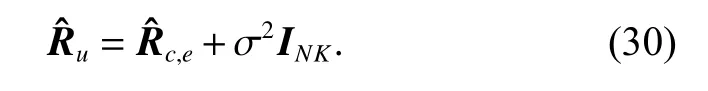
Then the STAP filter weight can be given as

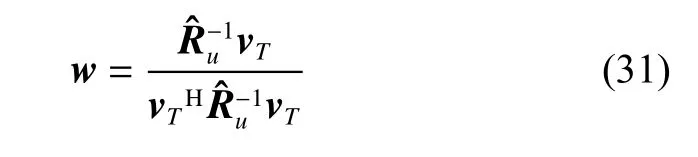
where vTis the target space-time steering vector, which can be expressed as

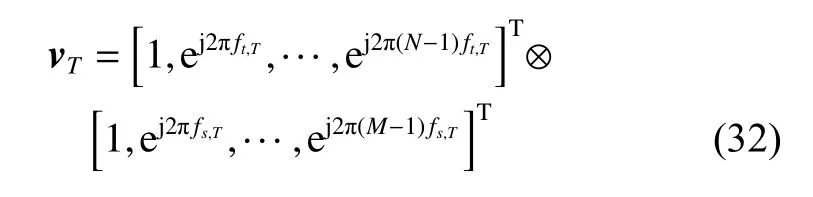
where ft,Tis the target normalized Doppler frequency and fs,Tis the target spatial frequency.

In summary, the detailed steps of the proposed ANMbased STAP method with the array amplitude-phase calibrated are shown as follows.

Step 1Estimate the array amplitude-phase error matrixusing the single auxiliary calibration algorithm.

Step 2Exploit the estimated array amplitude-phase error matrixto reconstruct the ANM problem (25), and then solve (25) to obtain

Step 3According to (26) and (27),are obtained.

Step 4Estimate the CNCMthrough (28), (29) and(30).

Step 5Calculate the STAP filter weight by (31).

According to the above analysis, the proposed ANMbased STAP method with the array amplitude-phase calibrated consists of the amplitude-phase error estimation, the clutter covariance matrix estimation and the computation of the STAP filter weight. The computation complexity of the amplitude-phase error estimation iswhere M is the number of snapshots for the single auxiliary calibration algorithm. For the clutter covariance matrix estimation, the calculation amount mainly depends on the solution of the semidefinite programming problem, whose computation complexity isThe computational burden of the estimation of the STAP filter weight rests with the CNCM inversion,whose computation complexity isThus, the computatio ncomplexity o fth epropose dmetho disO

4. Simulation experiment

In this section, simulation results are used to verify the performance of the proposed method. The relevant parameters used in the simulations are listed in Table 1. Assume that the amplitude-phase errors follow uniform distribution (UD), and four different levels of the amplitudephase are defined as “level1”, “level2”, “level3” and“level4”, which are subject to UD as (-0.1,0.1)/(-0.25,0.25), (-0.2,0.2)/(-0.5,0.5), (-0.5,0.5)/(-2.5°,2.5°), and(-1,1)/(-2.8°,2.8°), respectively. For the ANM-STAP algorithm, the number of training snapshots is assumed to be 5. The number of snapshots of the error calibration algorithm is 100. The simulation results are averaged through 100 independent Monte Carlo runs. In addition,to confirm the clutter suppression performance of the proposed method, the signal-to-interference-plus-noise ratio(SINR) loss is utilized, which is defined as

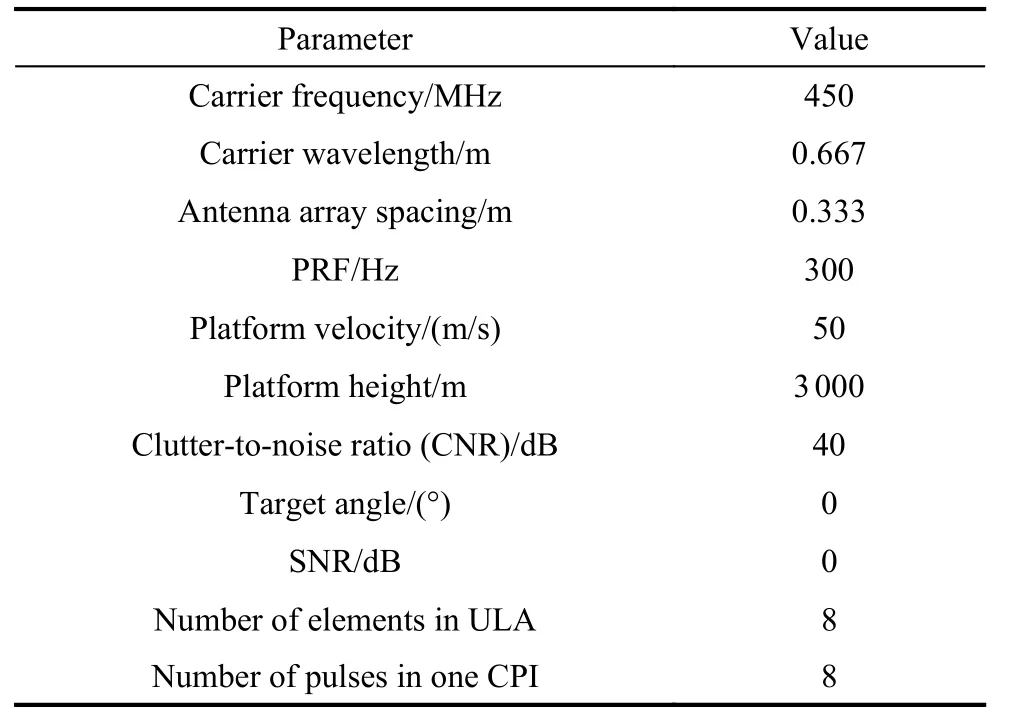
Table 1 Radar system parameters

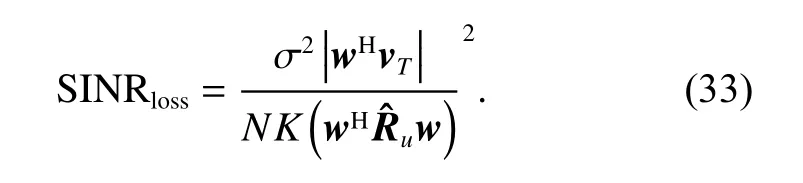
In the first simulation, to evaluate the accuracy of the CNCM estimated by different methods, Capon spectrum and eigenspectra of the CNCM are illustrated in this subsection. Fig. 1(a) shows the Capon spectrum of clutter calculated by the optimal STAP with the known CNCM.Fig. 1(b) and Fig. 1(c) provide the clutter Capon spectrum estimated by the ANM-based STAP without and with array amplitude-phase error calibration, respectively.As shown in Fig. 1(a), the clutter is only disturbed as a ridge in the whole angle-Doppler plane. It can be seen from Fig. 1(b) that the estimation result of the conventional ANM-based STAP method has some outliers circled, which are caused by the array amplitude-phase error. These outliers directly result in the inaccurate clutter subspace and CCM estimation, which degrades the clutter suppression performance. Fig. 1(c) shows that the clutter distribution in the angle-Doppler domain is similar to the optimum case in Fig. 1(a), which is estimated by the ANM-based STAP method with calibration. Thus,after the array amplitude-phase error correction, the estimation accuracy of the CNCM can be improved.

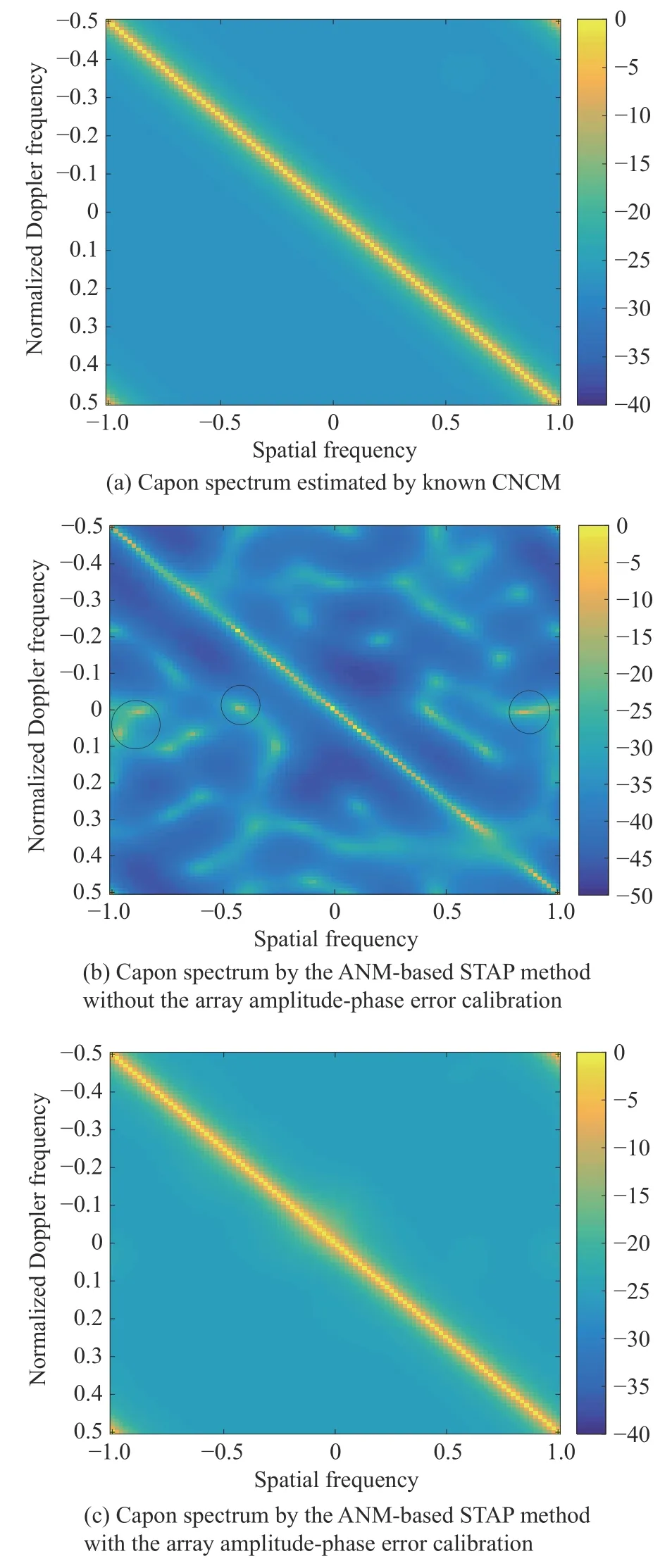
Fig. 1 CNCM estimation results based on different methods

In Fig. 2, the eigenspectra of the optimum CNCM and the estimated CNCM are shown. The label named “Optimal” in Fig. 2 represents the eigenspectra obtained by the known CNCM. It can be observed that the eigenspectra falls off gradually in all cases, and the theoretical rank of the CCM is shown by the vertical line. Fig. 2 also shows that the eigenspectra obtained by the proposed algorithm exhibits the similar form with the optimal one,which is in accordance with the analysis of the clutter rank with the amplitude-phase error.

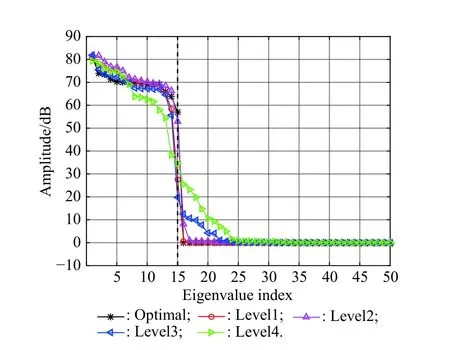
Fig. 2 Eigenspectra of CNCM at four different error levels

The second simulation focuses on the influence of different levels of the amplitude-phase error on the ANMbased STAP method without considering the array amplitude-phase error [18]. The label shown in Fig. 3, named“Optimal”, represents the optimum output SINR loss of the error at “Level1” precisely calibrated. The remainder curves in Fig. 3 represent the SINR loss of the ANMbased STAP algorithm without calibration at four different array amplitude-phase error levels. It can be observed from Fig. 3 that the performance of the ANM-based STAP algorithm with four different error levels all degrades compared with the optimum output SINR loss.Therefore, there is a negative influence on the performance without error calibration. This is why the array amplitude-phase error must be considered in the ANM-based method in practice.

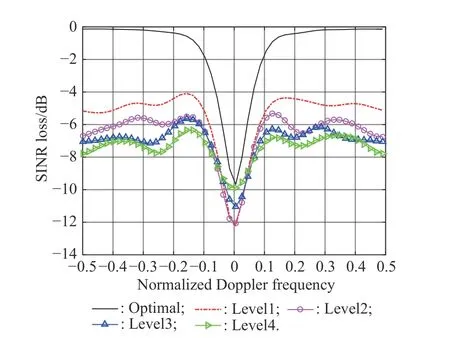
Fig. 3 SINR loss of the ANM-based STAP method without calibration at four different error levels

In the third simulation, the performance of our proposed ANM-based STAP method with the error calibration algorithm is evaluated. Simulation results are shown in Fig. 4 and Fig. 5. The labels in Fig. 4 “With calibration”and “Without calibration” represent the performance of ANM-STAP with and without the amplitude-phase error calibration. Fig. 4 compares the performance of the ANMbased STAP method with and without the error calibration at “Level1”. It can be learned that the performance of the ANM-based STAP method with the error calibration is improved compared with the ANM-based STAP method without calibration.

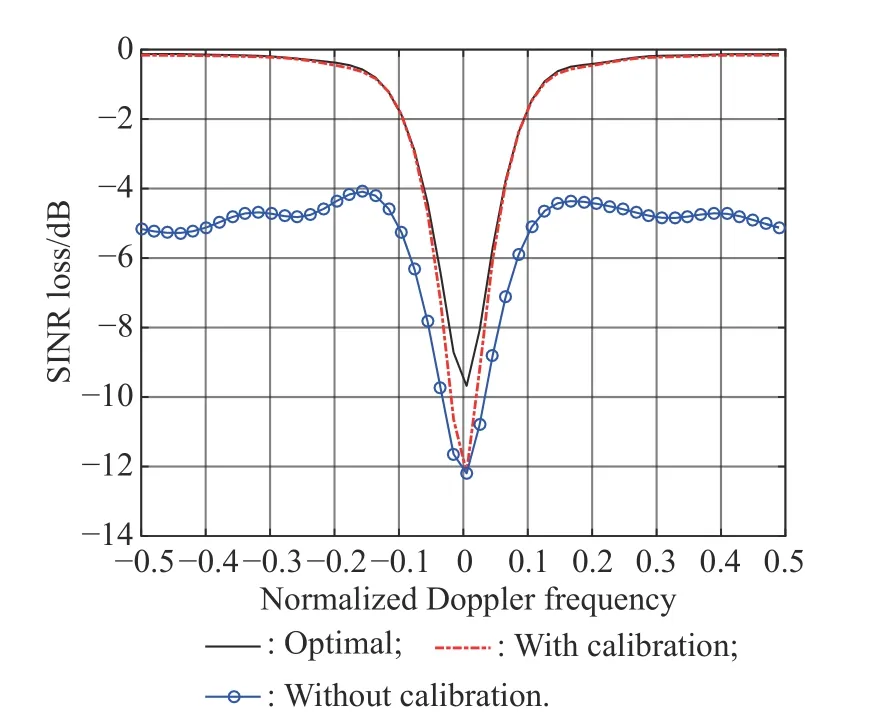
Fig. 4 SINR loss of ANM-based STAP method with and without calibration at “Level1”

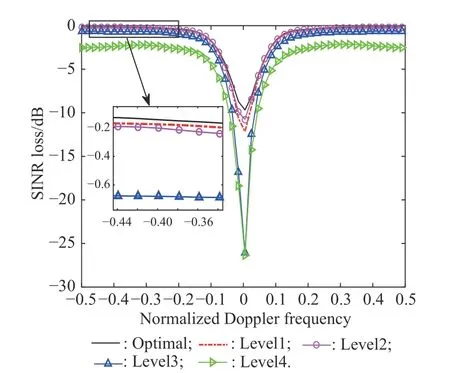
Fig. 5 SINR loss of ANM-based method at four different level errors

Fig. 5 shows the performance of the ANM-based algorithm with four different level errors. It can be found from Fig. 5 that the performance of the ANM-based STAP method with the error calibration is close to the optimum performance while the performance degrades with different amplitude-phase errors. Hence, in the presence of the amplitude-phase errors the performance of the ANM-based STAP method will be improved by pre-estimating the amplitude-phase error information.

In the fourth simulation experiment, we make the clutter suppression performance comparison of the proposed method, the sparsity-based STAP considering array gain/phase error (AGPE-STAP) method [27], and the iterative alternating descent sparse recovery STAP (IAD-SR-STAP)method [28] to highlight the superiority of the proposed method. The above three methods all carry out the amplitude-phase error estimation. In this simulation experiment, the amplitude-phase error follows UD as (-0.5,0.5)/(-2.5°,2.5°). As shown in Fig. 6, the clutter suppression performance is evaluated through the SINR loss. From Fig. 6, we can observe the proposed method has a narrower notch than other methods. Since the proposed method is presented in a continuous domain, the off-grid problem can be avoided, which causes that the proposed method has a better clutter rejection performance than the AGPE-STAP method and the IAD-SR-STAP method.

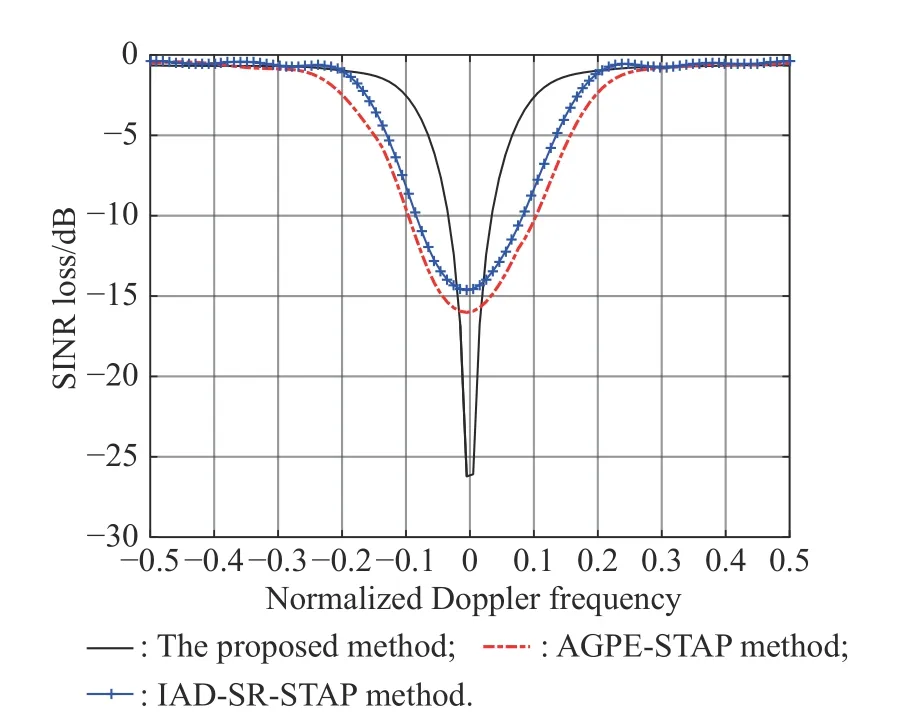
Fig. 6 SINR loss of three different methods

In order to further verify the correctness and effectiveness of the proposed method, the public MountainTop data [31] is used in the fifth simulation, whose system parameters are N=14 and K=16. Moreover, the major clutter is located at θ=−25°and fd=0.3. Fig. 7 depicts the SINR loss of different methods over the normalized Doppler frequency. From Fig. 7, it can be seen that the proposed method has a narrower notch compared with the AGPE-STAP method and the IAD-SR-STAP method at the major clutter area. Hence, Fig. 7 demonstrates that the proposed method has a better CCM estimation and rejection performance than other methods.

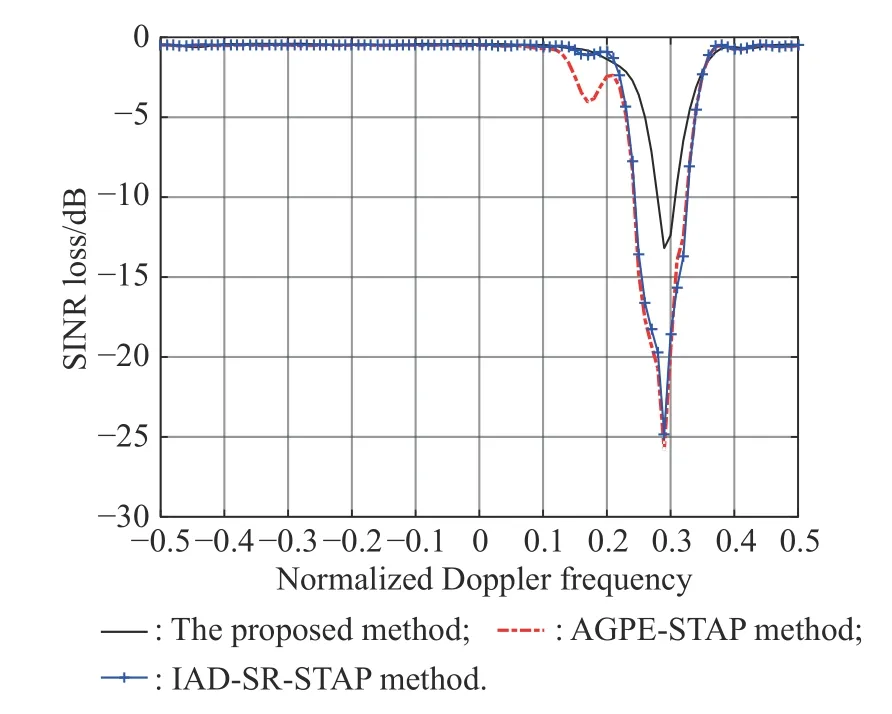
Fig. 7 SINR loss of the measured data

5. Conclusions

In this section, simulation results are used to verify the performance of the proposed method.

An ANM-based STAP method with the array amplitude-phase error calibrated is proposed to suppress the clutter and detect the target for airborne radar. The proposed method first estimates the array amplitude-phase error information. Then, according to array amplitudephase error information obtained, a modified ANM problem is established. Since the array amplitude-phase error is calibrated, the proposed method performs better compared with the conventional ANM-based STAP method.Meanwhile, because the proposed method is established in a continuous domain, its performance precedes the methods based on sparse recovery. Simulation results verify the superior performance of the proposed method.

Since the proposed method needs to solve the semidefinite programming problem, the computational burden is a considerable problem, which is difficult to satisfy the real-time requirements. Hence, the further work is to combine the methods with more efficient computation to solve the computational burden of the proposed ANMbased method.