Fast and accurate covariance matrix reconstruction for adaptive beamforming using Gauss-Legendre quadrature

LIU Shuai, ZHANG Xue, YAN Fenggang, WANG Jun, and JIN Ming

School of Information Science and Engineering, Harbin Institute of Technology, Weihai 264209, China

Abstract: Most of the reconstruction-based robust adaptive beamforming (RAB) algorithms require the covariance matrix reconstruction (CMR) by high-complexity integral computation. A Gauss-Legendre quadrature (GLQ) method with the highest algebraic precision in the interpolation-type quadrature is proposed to reduce the complexity. The interference angular sector in RAB is regarded as the GLQ integral range, and the zeros of the threeorder Legendre orthogonal polynomial is selected as the GLQ nodes. Consequently, the CMR can be efficiently obtained by simple summation with respect to the three GLQ nodes without integral. The new method has significantly reduced the complexity as compared to most state-of-the-art reconstruction-based RAB techniques, and it is able to provide the similar performance close to the optimal. These advantages are verified by numerical simulations.

Keywords: robust adaptive beamforming (RAB), covariance matrix reconstruction (CMR), Gauss-Legendre quadrature (GLQ),complexity reduction.

1. Introduction

Adaptive beamformers have been widely used to enhance the desired signal and suppress interferences in radar,wireless communication and other fields [1-3]. The minimum variance distortionless response (MVDR) beamformer is an optimal beamformer when the exact knowledge of the desired signal steering vector is available and the covariance matrix does not contain the desired signal component. Thus, the beamformer shows both an optimal output signal-to-interference-plus-noise ratio (SINR) and a high convergence rate. However, many nonideal factors lead to steering vector mismatch, such as pointing error,array element position error and antenna array calibration error in many applications [4,5]. Adaptive beamformers are sensitive to model mismatch, especially when the desired signal is present in the training data [6,7].

Recently, a robust adaptive beamforming (RAB) algorithm based on the covariance matrix reconstruction(CMR) technique has been proposed. The interferenceplus-noise covariance matrix was firstly reconstructed by utilizing the Capon spectral estimator integrated over an angular sector separated from the desired signal direction[8], and this method was more robust than using the sample covariance matrix. Many other improved algorithms based on the Capon spectral estimator integration optimize the performance of CMR in different aspects [9-12].However, CMR has high-complexity integral computation, which limits the computational efficiency. In this paper, we focus on introducing an improved version of the integral method using Gauss-Legendre quadrature(GLQ) to obtain abundant complexity reduction for fast and accurate RAB in the CMR stage. The proposed method performs a simple summation with respect to the three GLQ nodes by selecting the roots of the three-order Legendre orthogonal polynomial as the GLQ nodes. Consequently, the CMR can be efficiently obtained without integral. Simulation results show that the computational efficiency of the proposed method is significantly improved. Meanwhile it can provide almost the similar performance as compared to the optimal.

2. Signal model and background

Consider a uniform linear array (ULA) composed of N omnidirectional sensors. Assume that one narrowband desired signal and one narrowband interference impinge on the array. The array output vector is expressed as

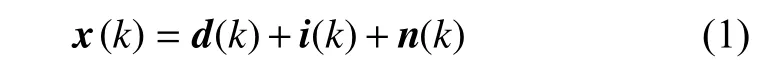
where d(k) , i(k) and n(k) are the desired signal, the interference and the noise component, respectively. The weight vector [8] is written as

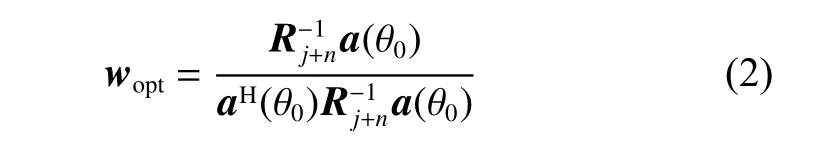
where

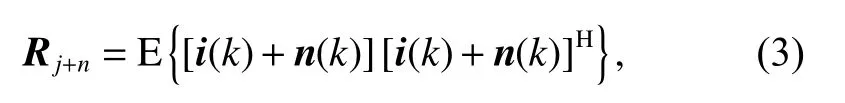
Rj+nis the interference-plus-noise covariance matrix, i(k)is the interference signal, a(θ0) is the desired signal steering vector and (·)Hstands for the Hermitian transpose. In practice, Rj+nis unavailable, and it can be computed by the CMR technique [8] as follows:

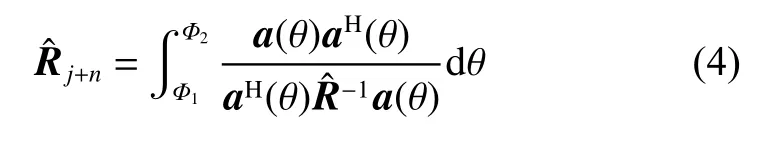
where a(θ) is the steering vector associated with a hypothetical interference direction θ based on the known array structure,is the sample covariance matrix,L is the number of snapshots,anddenotes the interference angular sector, which contains the interfering signal sources but not the desired signal.

The traditional quadrature method [8-12] approximates the integral with the summation

where a(θm) is the steering vector associated with direction θm∈[Φ1,Φ2] (m=1,···,M), and M is the number of sample points. To guarantee sufficient accurate approximation, one has to perform a fine sampling with a much bigger number M. As the computational complexity of CMR is proportional to M, the computation of CMR is time-consuming, and there is a need for techniques demanding fast CMR computations.

3. The proposed algorithm

Considering that integral summation of M points given in(5) is very complex when M is large, a matrix reconstruction method based on GLQ is proposed in this paper. The Gaussian quadrature formula is known to have the highest algebraic precision among the interpolation-type quadrature formulas [13-15]. Taking the trade-off between computational complexity and algebraic precision into account, we choose three-point GLQ to estimatewith the equation

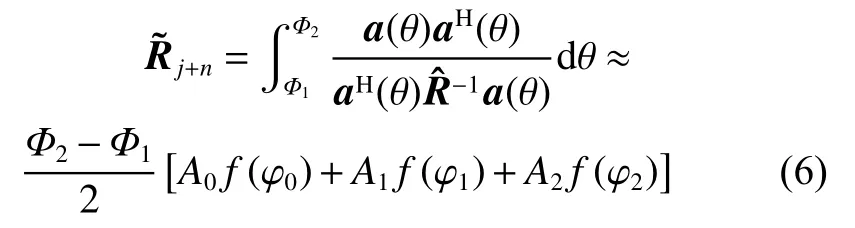
where

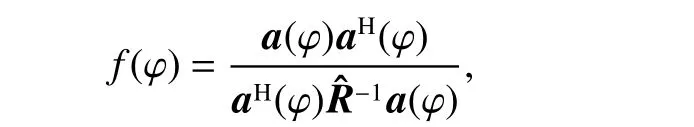
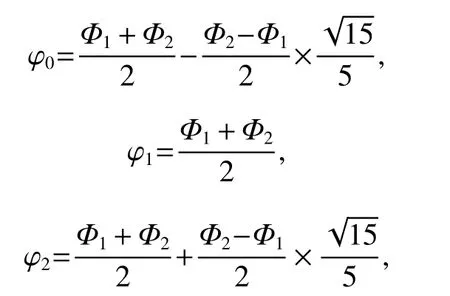
Equation (6) can be deduced as follows.

The generalized interpolation-type quadrature formula for n+1 points is given by

where xj(j=0,1,···,n) are the integral nodes, a and b are the interval endpoints, Aj(j=0,1,···,n) are weights, and E(f)is the integral remainder (residual error).

If the integral node of the Gaussian quadrature formula is chosen as the roots of Legendre polynomial, the quadrature formula formed in this way is called GLQ formula.The Legendre polynomial sequence is shown in

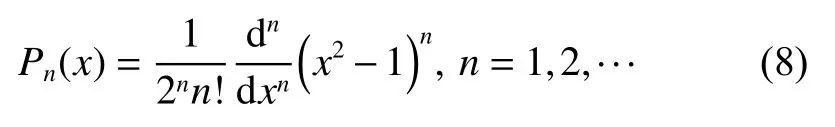
The explicit expressions for (8) can be obtained by using the recursive formula (n+1)Pn+1=(2n+1)xPn−nPn−1as

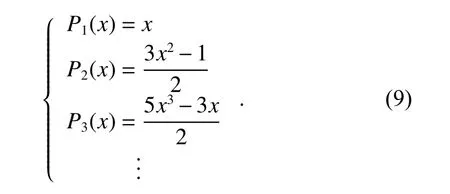
We choose three-point GLQ [14], which guarantees algebraic precision with low computational complexity as

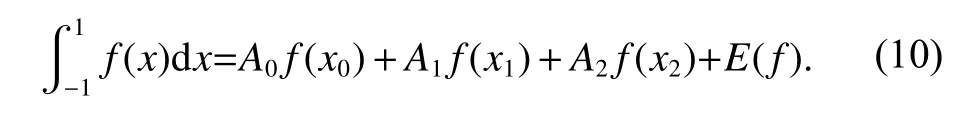
From 3-order Legendre polynomial P3(x)=(5x3−3x)/2,we can solve the roots ofas integral nodes.

According to the GLQ theory, the 3-order Legendre polynomial quadrature has at least 3-order algebraic precision. It means that when f(x)=1, f(x)=x , f(x)=x2, the following equations hold:

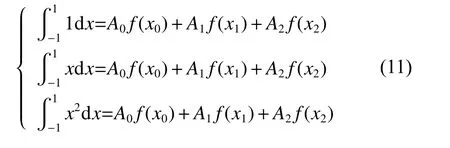
which means that

Thus, the three weights are A0=5/9 , A1=8/9 , A2=5/9.

Omitting the remainder E (f), we can express (10) as

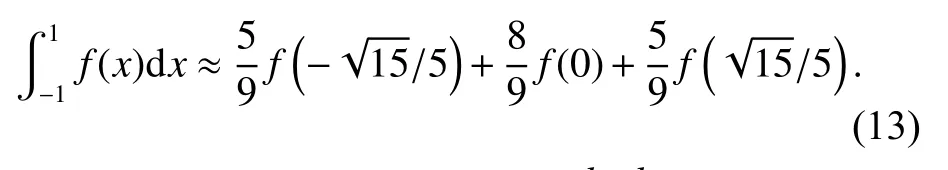
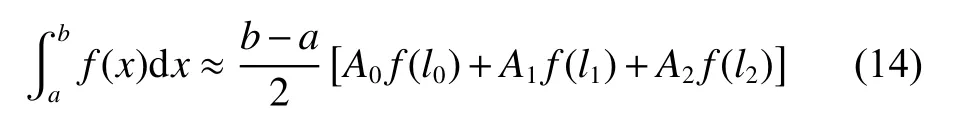
According to (14), the integrating of=can be expressed as (6).

The desired signal steering vectorcan be computed by[12].Therefore, the weight vector of the proposed approach is computed as

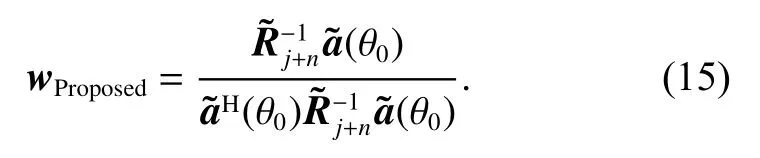
For a complexity point of view, compared with Mpoint accumulation of traditional matrix reconstruction(5), we utilize the weighted summation of 3-point integral expressions to reconstruct covariance matrix (16). The ratio of the computational complexity between the proposed and the classical method is about 3:M. It achieves a win-win situation in computational efficiency and excellent performance as compared to most state-of-the-art reconstruction-based RAB techniques.

4. Simulation

Experiments with 500 independent Monte Carlo trials are implemented to examine the performance of the proposed GLQ method with comparison between CMR quadratically constrained quadratic programming (CMR-QCQP) beamformer [8], CMR-Sub beamformer [12], MVDR,and diagonal loading (DL) beamformer[16]. For fair comparisons, a half-wavelength ULA with N=8 omnidirectional sensors is considered. The number of snapshots is set as L=200 and the direction of the desired signal impinged on the array is assumed as θ0=0°. The input signal-to-noise ratio (SNR) is 10 dB. The interference direction is θ =45°and the interference-to-noise ratio (INR)is 30 dB.

In order to evaluate the performance of the reconstruction matrixwe use the correlation coefficient [12]between the reconstruction matrixand theoreticalas

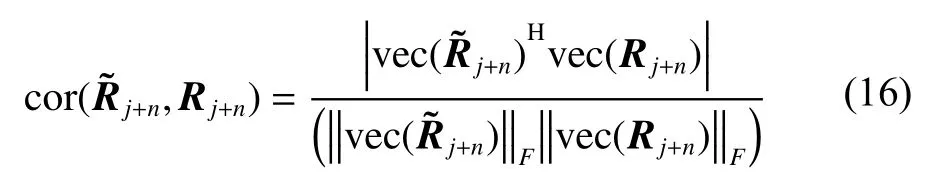
where vec(·) is a vector got by stacking the columns of a matrix on top of each other, and ‖·‖Fdenotes the Frobenius norm.

First, we compare the correlation coefficient of the proposed GLQ reconstructedthe reconstructed interference-plus-noise covariance matrix of the other two representative reconstruction-based beamformers with different sample points [8,12] to the theoretical Rj+nand their own correlation coefficients versus the input SNR and snapshots are drawn in Fig. 1 and Fig. 2 respectively.

Fig. 1 Coefficient of covariance matrix versus input SNR, L=200,INR=30 dB, two signals at θ0=0° and θ=45°

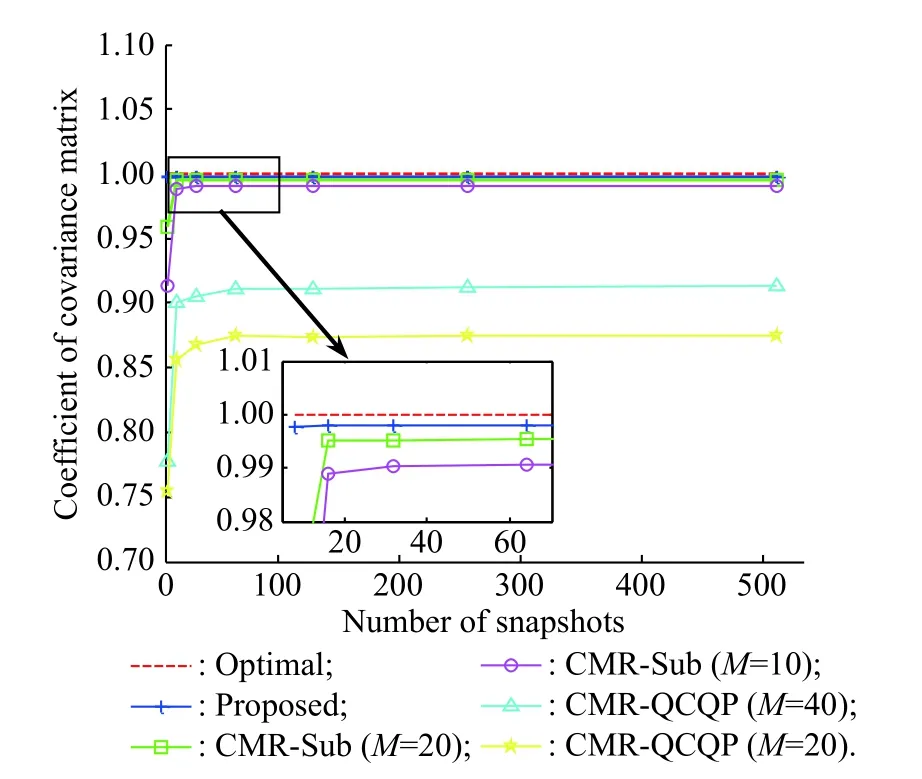
Fig. 2 Coefficient of covariance matrix versus snapshots, SNR=10 dB, INR=30 dB, two signals at θ0=0° and θ=45°

It can be seen from Fig. 1 and Fig. 2 that the proposed method provides the similar correlation coefficient as the optimal, which is much better than CMR-sub and CMRQCQP.

Then, we compare the proposed method with (5) in terms of the matrix reconstruction complexity, where the computational efficiency is equivalently evaluated with CPU times by running codes in the same computer environment. Fig. 3 displays the simulation time versus the number of sensors, where the simulation time is given by a PC with Intel(R) Core(TM) i5-8 400 CPU @ 2.80 GHz and 8 GB RAM.

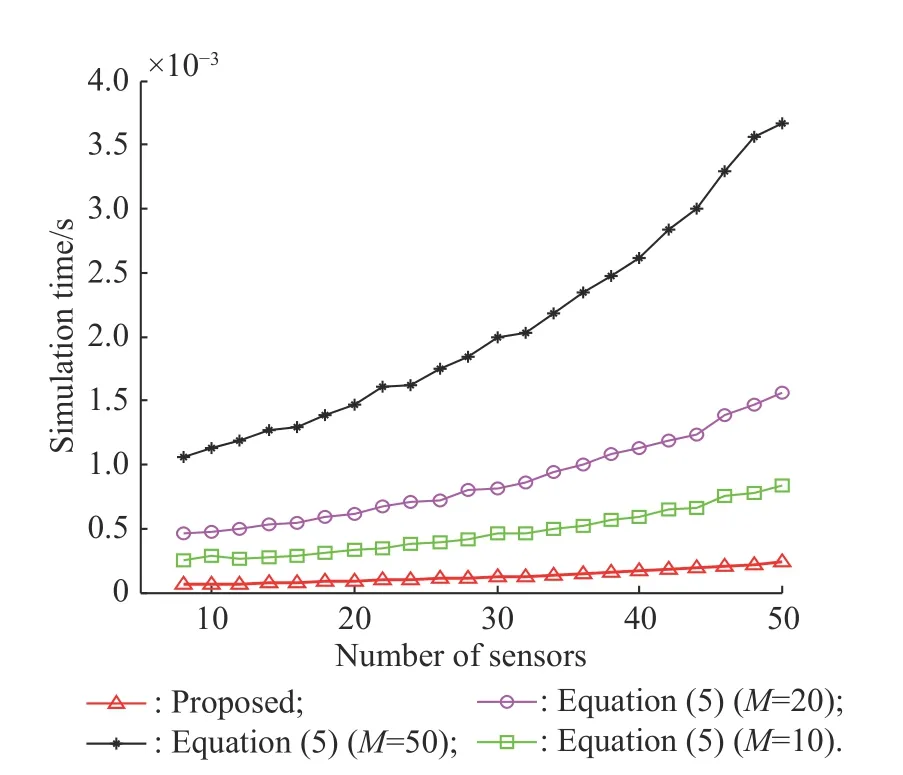
Fig. 3 Comparison of simulation time versus number of sensors,L=200, SNR=10 dB, INR=30 dB, two signals at θ0=0° and θ=45°

Fig. 3 shows that the proposed method can greatly improve the computational efficiency of the matrix reconstruction compared with the classical method. Taking eight sensors as an example, the proposed method takes 64 μs, the time-consuming of (5) is 246 μs, 460 μs and 1 062 μs, corresponding to the M of 10, 20, 50 respectively. The ratio of time-consuming with four curves at eight sensors is 1:3.8:7.2:16.6, which is basically consistent with the theoretical analysis result 3:M.

Next, we plot the output SINR as functions of the SNR and snapshots respectively, where SNR varies in the range from -10 dB to 20 dB, and the numbers of snapshots are selected as 8, 16, 32, 64, 128, 256, 512.

It can be concluded from Fig. 4 and Fig. 5 that the proposed method outperforms MVDR, DL, CMR-Sub and CMR-QCQP algorithm with all SNRs and snapshots slightly, moreover it shows a similar performance as compared to the optimal. Mismatch due to the signal direction error caused by the estimated method is very common in practical application. The impact of the signal direction error on output SINR is considered. Assume that the direction error of the desired signal changes from -10° to 10°, the output SINR is counted and shown in Fig. 6.

It can be seen from Fig. 6 that even the small mismatch direction error of the MVDR algorithm will cause serious degradation of algorithm performance; DL improves the sensitivity to the direction error to a certain extent, but when the mismatch angle is greater than 2°, the algorithm performance will degrade seriously. The proposed method which has a higher output SINR than the CMR-Sub and CMR-QCQP algorithms is robust to the mismatch direction error, as well as closer to the optimal.

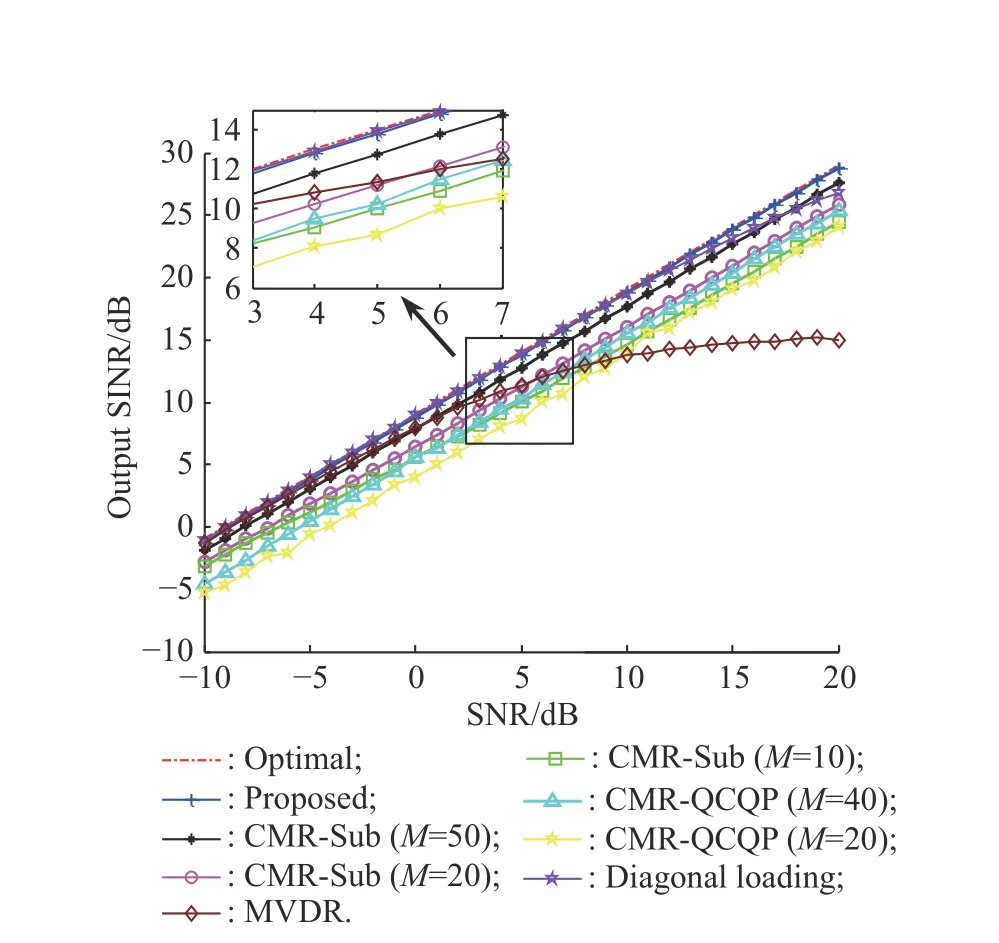
Fig. 4 Output SINR versus SNRs, N=8, L=200, INR=30 dB, two signals at θ0=0° and θ=45°

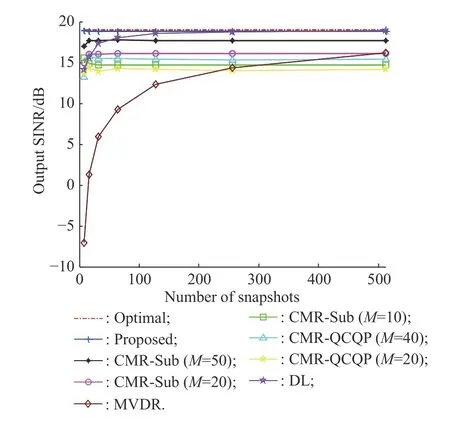
Fig. 5 Output SINR versus snapshots, N=8, SNR=10 dB, INR=30 dB, two signals at θ0=0° and θ=45°

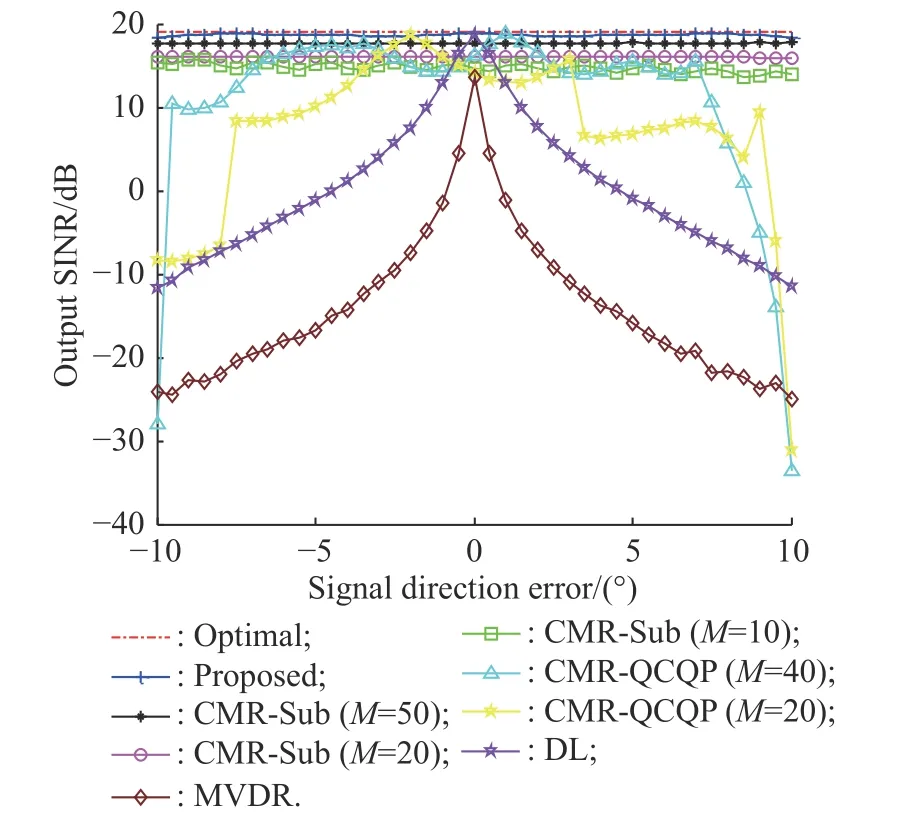
Fig. 6 Output SINR versus signal direction error, N=8, L=200,SNR = 10 dB, INR=30 dB, two signals at θ0=0° and θ=45°

The multipath scattering caused by local scatters can produce incoherent scattering, which is very common in radar and sonar applications. Assume that the desired signal has a time-varying steering vector, which can be modeled [17] as

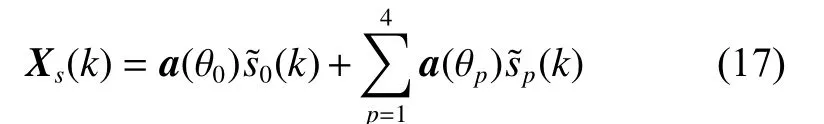
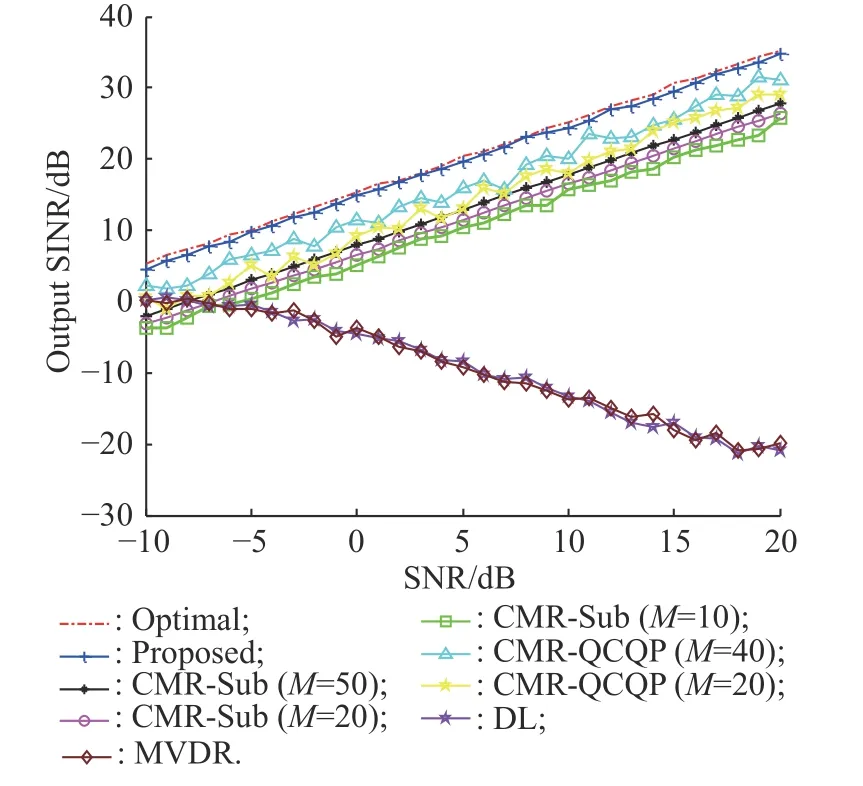
Fig. 7 Output SINR versus SNRs in the case of incoherent local scattering error, N=8, L=200, INR=30 dB, two signals at θ0=0° and θ=45°

It can be seen from Fig. 7 that the performance of the MVDR and the DL algorithm decreases when SNR ＞-5 dB; the performance of the proposed method is better than the classical CMR-QCQP and the CMR-Sub reconstruction method, which is always close to the optimal,and has better performance in the case of local incoherent scattering.

5. Conclusions

We propose a fast and accurate CMR computation method for RAB by using the GLQ with high algebraic precision. The new method transforms the high-complexity integral computation into a simple three-point summation with respect to three GLQ nodes, in which the interference angular sector is regarded as the GLQ integral range. Simulation results demonstrate that the proposed method improves the computational efficiency significantly with superior performance.