Reactive scheduling of multiple EOSs under cloud uncertainties: model and algorithms

WANG Jianjiang, HU Xuejun, and HE Chuan

1. College of Systems Engineering, National University of Defense Technology, Changsha 410073, China;2. Business School, Hunan University, Changsha 410082, China;3. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China

Abstract: Most earth observation satellites (EOSs) are low-orbit satellites equipped with optical sensors that cannot see through clouds. Hence, cloud coverage, high dynamics, and cloud uncertainties are important issues in the scheduling of EOSs. The proactive-reactive scheduling framework has been proven to be effective and efficient for the uncertain scheduling problem and has been extensively employed. Numerous studies have been conducted on methods for the proactive scheduling of EOSs, including expectation, chance-constrained, and robust optimization models and the relevant solution algorithms. This study focuses on the reactive scheduling of EOSs under cloud uncertainties. First, using an example, we describe the reactive scheduling problem in detail, clarifying its significance and key issues.Considering the two key objectives of observation profits and scheduling stability, we construct a multi-objective optimization mathematical model. Then, we obtain the possible disruptions of EOS scheduling during execution under cloud uncertainties,adopting an event-driven policy for the reactive scheduling. For the different disruptions, different reactive scheduling algorithms are designed. Finally, numerous simulation experiments are conducted to verify the feasibility and effectiveness of the proposed reactive scheduling algorithms. The experimental results show that the reactive scheduling algorithms can both improve observation profits and reduce system perturbations.

Keywords: earth observation satellite (EOS), uncertainty of clouds,reactive scheduling, multi-objective optimization, event-driven,heuristic.

1. Introduction

Earth observation satellites (EOSs) are platforms equipped with sensors that orbit the earth to take photographs of areas of interest [1,2]. EOS scheduling is aimed at allocating users ’ observation requests, e.g., for battlefield reconnaissance, disaster surveillance, urban planning, crop monitoring, to satellites. Although EOSs have increased considerably in quantity, they are still very scarcely compared to the explosively increasing number of applications. Hence, EOS scheduling is significant for obtaining high observation effectiveness and efficiency.

Several studies focusing on EOS scheduling have been conducted. With respect to the problem formulation, major research efforts have concentrated on mathematical programming [1,3-5], constraint satisfaction formulations [6,7], knapsack formulations [8], and graph-based formulations [9-11]. Furthermore, a considerable number of solution approaches for EOS scheduling have been proposed. They can be classified into three categories.First, exact solution algorithms contain branch-and-bound[12], dynamic programming [4,13,14], and branch-andprice algorithms [15]. Second, the vast majority of solution algorithms are metaheuristics, such as tabu search[1,11,16,17], evolution [9,18-20], ant colony [21,22],local search-based [23-26], and simulated annealing algorithms [27-29]. Finally, there are studies on heuristic algorithms for EOS scheduling, including constructive algorithms based on priority rules [30-35] and Lagrange relaxation heuristics [5].

All the aforementioned studies focused on the scheduling of EOSs in a deterministic environment without considering the impact of clouds. However, most EOSs are equipped with optical sensors that cannot see through clouds, which considerably affect and block the observations [27]. According to the statistics, approximately 80%of the observations from the optical SPOT satellites are useless because of the presence of clouds [36]. Hence,cloud coverage is an essential issue for EOS scheduling and cannot be neglected. Lin et al. [37] formulated the presence of clouds as a set of covered time windows and obtained the blocked parts of the time windows. In sequence, the tasks were forbidden to be observed in the blocked parts. However, their studies are infeasible in practice because the presence of clouds cannot be precisely forecasted [38].

The unpredictability of clouds creates difficulties and challenges for EOS scheduling. Hence, this issue is gaining more research attention. In general, there are two approaches for dealing with uncertainties in an EOS scheduling environment: proactive and reactive scheduling.Proactive scheduling produces a protected baseline schedule (initial schedule) by exploiting cloud forecast information. In proactive scheduling, each task is enabled to be completed successfully at a high probability. Liao and Tang [39] formulated the presence of clouds for each observation window as a stochastic event. Furthermore,they established a model with the objective of maximizing the weighted sum of the observation profits and the expected number of executed tasks. Valicka et al. [40]first suggested a new deterministic mixed-integer programming (MIP) model for the scheduling of multiple EOSs.Furthermore, considering the failure of observations due to the presence of clouds, they extended the deterministic MIP model to two- and three-stage stochastic MIP models. Wang et al. also considered the presence of clouds as stochastic events and established expectation, chanceconstrained, and robust optimization models in [2], [41]and [42], respectively. To solve the different models, a branch-and-price algorithm, a branch-and-cut algorithm,and some heuristics are suggested, respectively.

Despite the protection included in the baseline schedule, disturbances resulting from the uncertainties of clouds may also result in deviations from the baseline schedule. Therefore, reactive scheduling procedures are required to repair the deviated or failed schedule during the execution to stabilize the schedule and to obtain higher scheduling profits. Beaumet et al. [36] investigated the reactive scheduling of a Pleiades satellite that is equipped with a cloud detection instrument, and the reactive decisions are made on board based on cloud detection results.

Although reactive scheduling methodologies have been studied extensively in production planning [43-45], relevant studies in EOS scheduling are still very limited. Regarding the reactive scheduling of satellites, the major challenge is the tight bound of the solution time. For instance, with respect to the Pleiades satellite, the cloud detection equipment points to the ground 30° with regard to a geocentric pointing. Also, we can only repair and modify the observation plan after obtaining the cloud covering information from the detection equipment. Because EOSs orbit the earth at a high speed, the available time for online decisions is limited.

In addition, EOSs occupy low-altitude orbits, and they are not constantly within the visibility of a ground control station (in fact, they are only visible for approximately 10% of the time). Under such conditions, decisions about the observations must be made on board. However,due to the complexity of the space environment and various electromagnetic interferences, the computing power of onboard processors is limited. Therefore, considering the time-efficiency requirements and the limitation of computing power, it is crucial to design succinct and efficient reactive scheduling strategies.

In this study, based on our previous studies on proactive scheduling [2,41,42], the reactive scheduling approaches for EOSs are examined in detail. Initially, from a comprehensive analysis, we obtain two critical criteria for reactive scheduling: the observation profits and scheduling stability. Then, a multi-objective optimization model is constructed. Afterwards, the possible perturbations during the execution of a baseline schedule are analyzed,and an event-driven reactive scheduling mechanism is suggested. Subsequently, with respect to different perturbations, efficient reactive scheduling algorithms based on task retraction and task swapping are developed. Finally, we conduct numerous simulation experiments to verify the performance of the reactive scheduling algorithm. Experimental results show that reactive scheduling can both improve scheduling efficiency and reduce interruptions.

The remainder of this paper is organized as follows. In the next section, we describe the reactive scheduling problem with a multi-objective mathematical model and analyze the possible disruptions. Section 3 proposes a novel reactive scheduling algorithm dealing with different disruptions. In Section 4, the numerical computational results of our approaches are presented. Section 5 offers conclusions and directions for future research.

2. Reactive EOS scheduling problem

EOS scheduling implies allocating the limited observation resources to different observation tasks, thus producing an observation plan. The resulting observation plan needs to satisfy the operational constraints and improve resource utilization.

If satellites and observation tasks are regarded as machines and jobs, respectively, the EOS scheduling problem can be viewed as a multi-machine scheduling problem. However, compared to the traditional multi-machine scheduling environment, there are several new characteristics for the scheduling of EOSs:

(i) Time window constraints: EOSs can observe targets when those targets are within the coverage area of the satellites, which means that the targets need to be visible to the satellites. Hence, there are time window constraints for EOS observation scheduling.

(ii) Setup time constraints: After observing a target, a satellite requires a sequence of transformation operations,such as sensor shutdown, slewing, attitude stability, and startup, to observe the next target. Hence, the setup time between two consecutive tasks should be sufficient.

(iii) Memory and energy constraints: Satellite observation consumes onboard memory and electric energy;slewing also consumes electric energy. Hence, the scheduling of EOS observations needs to satisfy the limitations of memory and energy.

(iv) Oversubscribed characteristic: Normally, for the traditional multi-machine scheduling problem, all the jobs are required to be scheduled, and the objective is to minimize the makespan or production cost. However, for the scheduling of EOSs, due to the limitations of resources and complexities of constraints, not all the observation tasks can be accomplished. Hence, we can only schedule a subset of observations, with the objective of maximizing observation profits.

With respect to the scheduling problem under uncertainties, both proactive and reactive algorithms are required in practice. Therefore, a proactive-reactive scheduling framework is proposed in this study, which is shown in Fig. 1. For the proactive scheduling, we conduct some comprehensive studies, including expectation, chance constrained, and robust optimization models, and utilize the relevant solution algorithms [2,41,42]. In this study,we focus on the reactive scheduling methods for the scheduling of EOSs under cloud uncertainties.

Fig. 1 Proactive-reactive scheduling framework

For the reactive scheduling of EOSs, the objectives should consist of maximizing the observation profits and minimizing the deviation/distance from the original schedule regarding the allocation of various tasks. It is well known that if a baseline schedule has been produced,users will implement their working plans accordingly. If the initial schedule has to be largely adjusted or rescheduled, it will have a fatal impact on the decisions of users and may affect the subsequent observations in an undesirable manner. Therefore, it is preferred that the reactive schedule minimally deviates from the baseline schedule.To further illustrate the relation between improving the expected profits (the scheduling performance) and maintaining the scheduling stability, an EOS scheduling instance is analyzed in the following.

2.1 Illustrative example

There are three tasks and three orbits in this problem instance. Table 1 outlines the following settings: profits of tasks, availabilities for observations, time windows, and probabilities of successful observations. The symbol “—”denotes that the orbit is not available for observing the task. Furthermore, for this description, the setup times between different tasks are assumed to be 0, and the memory and energy capacity for each orbit is set to +∞; thus,we do not consider the memory and energy constraints.

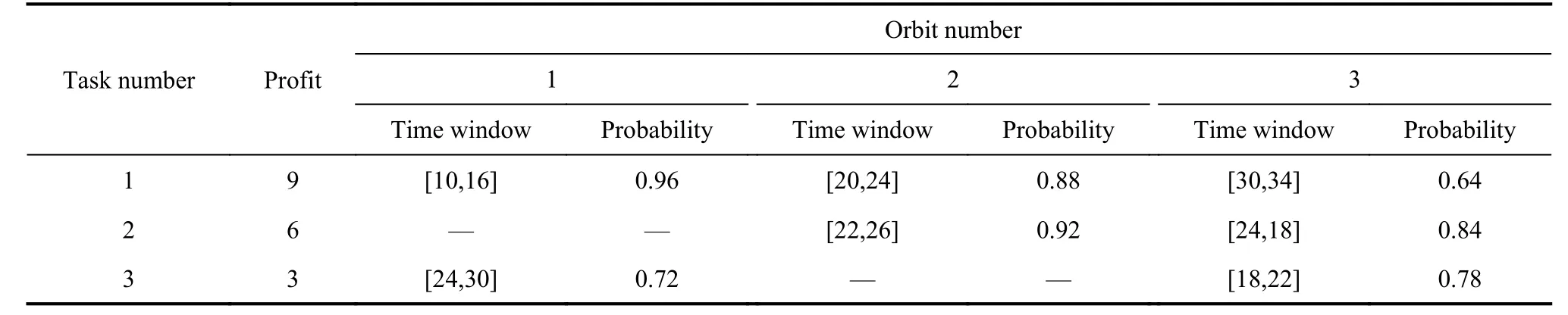
Table 1 Simulated EOS scheduling instance

For this example, the expectation model developed in our previous work [42] is used to construct a baseline schedule (see Fig. 2), in which the expected profit of the accomplished observation tasks is 16.5. During the execution process, the cloud detector perceives that task 1 will fail to be observed because of the presence of clouds.If we do not consider the reactive scheduling process, the profit from the derived schedule after this disruption will be reduced to 7.86, as shown in Fig. 3.

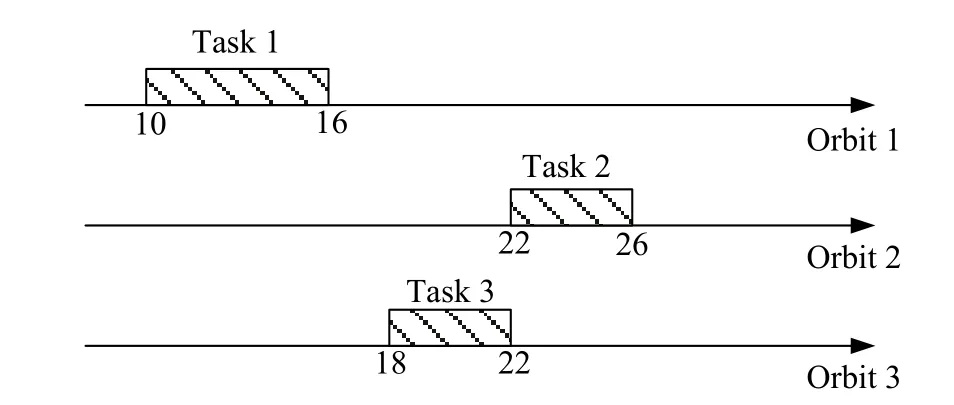
Fig. 2 Baseline schedule

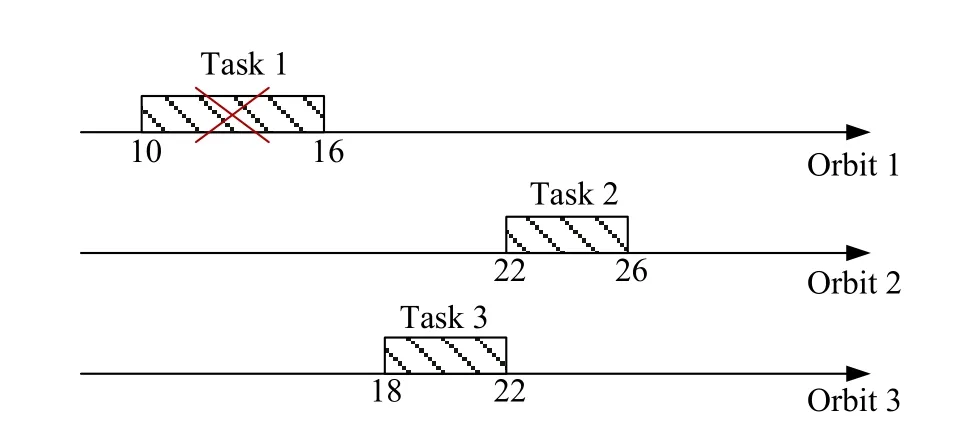
Fig. 3 New schedule after disruption (without reactive scheduling)

If we decide to employ a reactive scheduling procedure that seeks to maximize the expected profit disregarding the scheduling stability, we will obtain a repaired schedule, as shown in Fig. 4, with the expected profit being 15.3. In this case, both tasks 1 and 2 have been adjusted in comparison to the baseline schedule, resulting in a reactive schedule with poor stability.

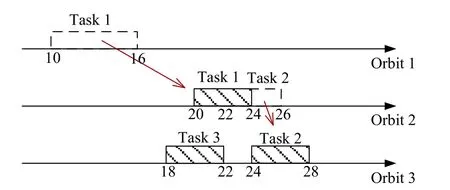
Fig. 4 Repaired schedule disregarding scheduling stability

Furthermore, an improved schedule can be created if we consider both the scheduling performance (with the value of the expected profit being 13.62) and the schedule stability, as shown in Fig. 5. In this case, only task 1 is adjusted, which means that the repaired schedule is more stable than the schedule shown in Fig. 4.

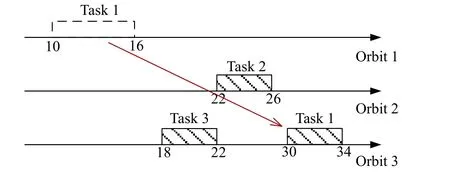
Fig. 5 Repaired schedule considering the scheduling stability

From the aforementioned example, we can conclude:(i) reactive scheduling can be effective against disturbances resulting from clouds and can improve the scheduling performance; (ii) it is often contradictory to enhance both the scheduling performance and the scheduling stability when the disrupted schedule is repaired, which inevitably results in a trade-off between these two key objectives.

2.2 Multi-objective reactive scheduling model

Reactive scheduling means timely repairing the baseline schedule according to cloud disruptions, guaranteeing the feasibility and successful implementation of the schedule.

If Sfrepresents the final schedule, the scheduling problem can be formulated as Sf={Sb,T,O,AO,Cons,Obj}.In detail, the six elements of the tuple are described as follows:

Sb: Proactive baseline schedule constructed using the expectation model [42], chance constrained programming (CCP) model [2], and the robust optimization model [41].

T: Set of tasks, T ={1,2,···,n}.T contains scheduled,unscheduled, and two dummy tasks {s,t}. Furthermore,i and j are indices of tasks in T, and each task i is associated with a profit ωi.

O: Set of orbits, O={1,2,···,m}. Each orbit k ∈O is associated with a memory capacity Mk, energy capacity Ek, memory consumption for each unit of observation time mk, and energy consumption for each unit of observation time ek.

AO: Set of available opportunities of observations,AO={ao1,1, ···, aon,1, ao1,2, ···,aon,2,···,ao1,m,···,aon,m}where a oikdenotes the available opportunity for task i on orbit k (i ∈T,k ∈O). Because we formulate the orbits of satellites as resources, there is at most one observation opportunity for each task in each orbit. A given available opportunity aoik∈AO is represented by aoik={[wsik,weik],θik}, where [wsik,weik] is the time window of observation, and θikis the slewing angle. Let bik=1 denote that task i can be observed on orbit k; thus, there are time windows for task i on orbit k , otherwise bik=0. In addition, the decision variables of our problem are(i,j ∈T ∪{s,t},k ∈O) , whereif both tasks i,j are scheduled on orbit k , and task i is the immediate predecessor of task j ; otherwise

Cons: Set of constraints that includes flow balance,availability, setup time, memory capacity, and energy capacity constraints.

(i) Flow balance constraints: The number of predecessors of each task should be equal to the number of its successors.

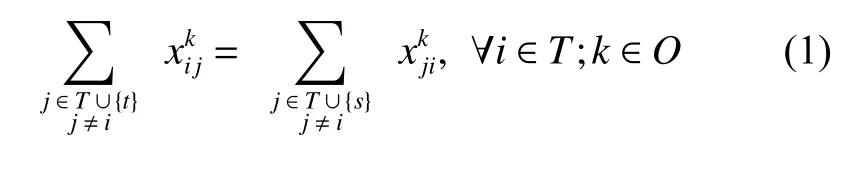
(ii) Availability constraints: Each task can only be scheduled to the orbits that are available for observing it.

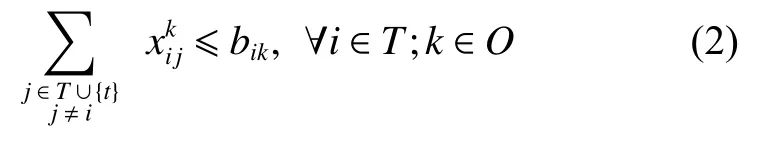
(iii) Setup time constraints: There should be a sufficient amount of setup time between consecutive tasks to facilitate the startup, shutdown, slewing, and stabilization operations of EOSs.

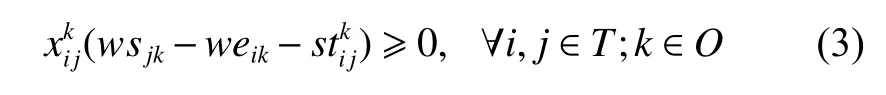
(iv) Memory capacity constraints: The memory consumption of the scheduled tasks cannot exceed the memory capacity for each orbit.

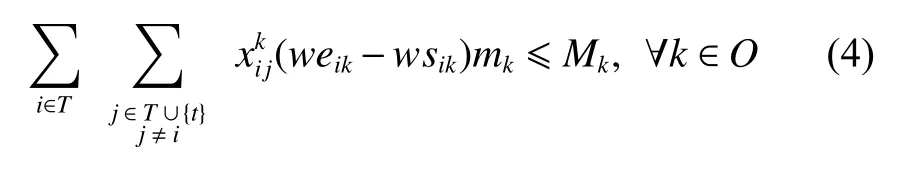
(v) Energy capacity constraints: The energy consumption of the task sequence must be less than or equal to the energy capacity for each orbit.

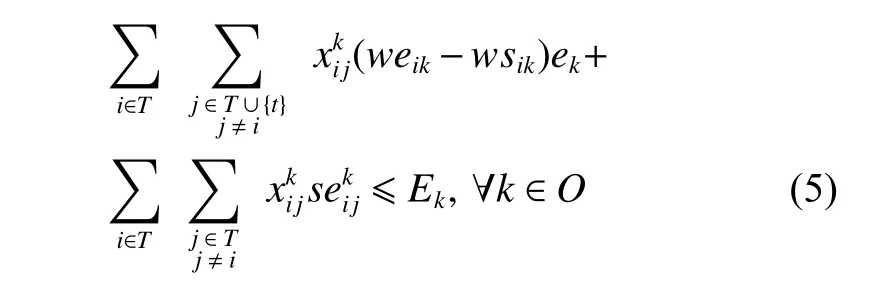
Obj : Scheduling objectives. In this study, we first consider maximizing the observation profits of the scheduled tasks under the operational constraints. Furthermore,to stabilize the schedule, we should minimize the perturbation while scheduling, i.e., minimizing the schedule distance, D(Sb,Sf), between the reactive and baseline schedules. In general, there are two types of disruptions during the implementation of an EOS schedule under cloud uncertainties.

(i) A task fails to be observed due to a blockage of clouds, and it cannot be repaired, implying that this task is absent in the final schedule;

(ii) The failed task can be repaired with a variance in the observation resource or observation time.

Therefore, the distance between the reactive and the baseline schedules can be defined as follows:

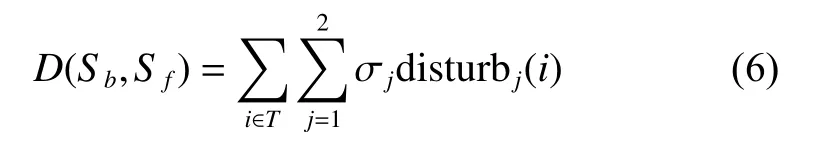
where σj(j=1,2) denotes the influence of the degree of disruption j (σ1＞＞σ2), and disturbj(i) represents the disruption count for task i in the entire scheduling.

Mathematically, the reactive scheduling problem is formulated as follows:

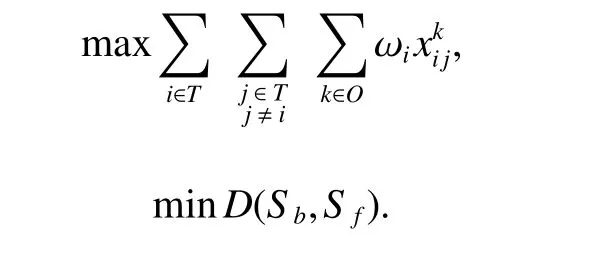
It is subject to constraints (i) – (v).

2.3 Reactive scheduling mechanism and disruption analysis

Reactive scheduling needs to address two key issues:(i) when to react to disruptions, namely, the specific schedule-driven policies, and (ii) the method(s) used to repair the existing schedule. This section mainly focuses on the first issue, and the suggested reactive scheduling algorithms are discussed in the next section.

In general, the driven strategies of reactive scheduling can be divided into three categories: periodic driven,event driven, and hybrid driven [46].

(i) Periodic driven: For this policy, a certain time period T is defined between any two rescheduling decision points. Once a reactive schedule is generated at some time t, no more rescheduling actions will be conducted until the next decision point t+T regardless of the possible disturbances. The merits of the periodic policy include simplicity and reliability. However, it cannot timely deal with disruptive events occurring between rescheduling points, which may result in delayed or infeasible plans in some cases.

(ii) Event driven: Under the event-driven policy, reactive scheduling is triggered in response to an unexpected event. This policy is normally able to cope well with disruptive events, whereas some reactions might be redundantly induced, particularly when there are several uncertain factors.

(iii) Hybrid driven: This policy is a combination of the aforementioned two approaches and relies on a periodic rescheduling at regular time period T, however, a rescheduling procedure can also be invoked if a fatal disruption is discovered.

Considering the characteristics of the EOS scheduling problem under uncertainties of clouds, this study adopts an event-driven policy to achieve a preferable schedule performance and to enforce the responsiveness capability to disturbances. In one of our previous studies, to ensure the successful completion of more tasks under cloud uncertainties, i.e., to make the schedule more robust, we consider scheduling a single task to multiple resources (orbits) [41]. As a consequence, there are two sets of scheduled tasks in an EOS schedule, one set of single-dispatch tasks and one set of multi-dispatch tasks. Based on this analysis, disruptive events that may trigger reactive scheduling can be classified into the following three categories:

(i) Failure of a single-dispatch task: If the observation of a single-dispatch task fails, we should retract this task from the schedule, generating two consequences. The first is that the retracted task cannot be executed because there is no other copy of the single-dispatch task in the schedule. The second is that the originally assigned timewindow resource of the retracted task will be unoccupied and wasted. Hence, in reactive scheduling, we need to not only reschedule the retracted task as far as possible but also schedule other tasks to the unoccupied time window to improve resource utilization and observation profit.

(ii) Failure of a multi-dispatch task: If the observation of a multi-dispatch task fails, we do not need to reschedule the failed task, because there are other copies and observation opportunities for the task in the schedule.However, we need to reassign other tasks to the unoccupied time window.

(iii) Success of a multi-dispatch task: If a copy of a multi-dispatch task is successfully executed, which implies that this multi-dispatch task has been finished, the remaining copies of this task in the schedule become useless and should be released; other unscheduled tasks will be rescheduled to the released time windows of the copies.

3. Reactive scheduling algorithms

Regarding the second issue, how to react to unexpected events, the literature provides two dominating approaches: complete rescheduling and schedule repair. Complete rescheduling creates a new schedule by treating all the uninitiated tasks as new tasks subjected to the operational constraints. While complete rescheduling can be efficient in achieving optimal solutions concerning traditional scheduling objectives, it normally results in a lack of continuity and relatively high instability costs, as shown in Subsection 2.1. Schedule repair refers to some local adjustments in the current schedule to recover the execution process. As the schedule repair method can increase the expected profits as well as preserve the stability of the system, it is highly preferred in practice. Hence, it is also used in this study. In the following section, specific reactive scheduling algorithms for the various disruptive events discussed in the previous section are proposed.

3.1 Failure of a single-dispatch task

As previously mentioned, when the observation of a single-dispatch task fails, we retract this task from the schedule and release the occupied time windows. Subsequently, other unscheduled tasks are reassigned to the released time windows to improve the observation efficiency. Finally, we try to schedule the retracted task to other time windows. Consequently, the reactive scheduling policy in this case is described in Algorithm 1.

Algorithm 1Reactive scheduling algorithm (failure of a single-dispatch task)

Step 1Retract the failed task i from the current schedule CurS ol, and release the time window resource[wsik,weik] of orbit k.

Step 2Select tasks from the set of unscheduled tasks UnScheTaskSet, and then try to schedule them to the time window [ wsik,weik]. See details in Algorithm 2.

Step 3Try to reassign the retracted task i to the other orbits. See details in Algorithm 3.

Before describing the details of Algorithm 2 and Algorithm 3, we first propose some definitions, as follows.

Definition 1Priority rule

The priority piof task i is defined as follows:

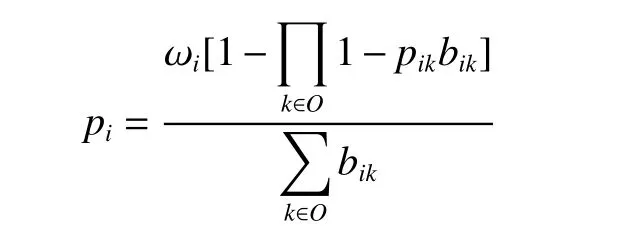
Definition 2Conflicting task set

A conflicting task set, Con fik, is defined as a set of conflicting tasks that are scheduled on orbit k and violate setup time constraints with task i.

Algorithm 2Reschedule the unscheduled tasks in UnScheTaskSet

Step 1Obtain the set of unscheduled tasks that are available to be scheduled to time window [ wsik,weik], denoted as S ubUnScheTaskSet .

Step 2If SubUnScheTaskSet=ϕ, which indicates that no unscheduled task can be scheduled to [wsik,weik],the algorithm ends; otherwise, go to Step 3.

Step 3Check whether there exists a task i that can be directly scheduled to [ wsik,weik] without extra task retraction or task swapping. If there is such a task i, schedule it to [wsik,weik], delete it from the unscheduled task set UnScheTaskSet, and the algorithm ends; otherwise, go to Step 4.

Step 4Select an unscheduled task i from SubUnSche-TaskSet based on a priority rule (see details in Definition 1),and then obtain all the conflicting tasks with task i on orbit k, constituting a conflicting task set Confik(see details in Definition 2). If Confik≠ϕ, go to Step 5; otherwise, choose the next task in SubUnScheTaskSet, and repeat Step 4.

Step 5Check whether all the tasks in the setCon fikare multi-dispatch tasks; if yes, retract all the tasks in Confikfrom the current schedule CurS ol. Subsequently,schedule task i to [wsik,weik], delete it from the unscheduled task set UnScheTaskSet, and the algorithm ends.Otherwise, go back to Step 4 and select the next task in SubUnScheTaskSet. If all the tasks in SubUnScheTask-Set have been visited, go to Step 6.

Step 6Revisit each task i in SubUnScheTaskSet. If Confik≠ϕ, go to Step 7; otherwise, select the next task from S ubUnScheTaskSet , and repeat Step 6.

Step 7Check whether all the tasks in Con fikhave been scheduled to other orbits. If all the single-dispatch tasks can be rescheduled, retract all the multi-dispatch tasks in Confikfrom the current schedule CurS ol . Then,reschedule the single-dispatch tasks in C onfik, reschedule task i to time window [wsik,weik], delete task i from SubUnScheTaskSet, and the algorithm ends. Otherwise,select the next task in S ubUnScheTaskSet, and go back to Step 6. If all the tasks in SubUnScheTaskSet have been visited, which means no task can be scheduled to[wsik,weik], the algorithm ends.

Algorithm 3Reschedule the retracted task i

Step 1Obtain the other observation opportunities Opporiof the failed task i .

Step 2If Oppori=ϕ, which implies that task i cannot be rescheduled, the algorithm ends; otherwise, go to Step 3.

Step 3In Oppori, check whether there exists a time window [wsik,weik] in which task i can be directly rescheduled without extra task retraction or task swapping.If there is such a time window, schedule task i to[wsik,weik], and the algorithm ends; otherwise, go to Step 4.

Step 4Select a time window [ wsik,weik] from the set Opporiin the ascending time order and obtain the conflicting task set C onfikof task i on orbit k . If C on fik≠ϕ,go to Step 5; otherwise, choose the next time window,and repeat Step 4.

Step 5Check whether all the tasks in the setCon fikare multi-dispatch tasks; if yes, retract all the tasks in Con fikfrom the current schedule CurSol. Subsequently,schedule task i to [wsik,weik], delete it from the unscheduled task set UnScheTaskSet , and the algorithm ends.Otherwise, go back to Step 4 and select the next time window in Oppori. If all the time windows inOpporihave been visited, go to Step 6.

Step 6Revisit each time window [wsik,weik] in Oppori. If C on fik≠ϕ, go to Step 7; otherwise, select the next time window from O ppori, and repeat Step 6.

Step 7Check whether all the tasks in Con fikhave been scheduled to other orbits. If all the single-dispatch tasks can be rescheduled, retract all the multi-dispatch tasks in Con fikfrom the current schedule CurSol. Then,reschedule the single-dispatch tasks in C on fik, reschedule task i to time window [ wsik,weik], and the algorithm ends.Otherwise, select the next time window in Oppori, and go back to Step 6. If all the time windows in O pporihave been visited, which means task i cannot be rescheduled,the algorithm ends.

Theorem 1Worst-case time complexity of Algorithm 1 is O (n3m+n2m2), in which n is the number of tasks and m is the number of orbits.

ProofFirst, the release of time windows of the failed task i will consume O(1) time, because a single-dispatch task will be only allocated once. (See Step 1 of Algorithm 1.)

In addition, the worst-case time complexity of the second step (Algorithm 2) is O(n3m). In detail, the time complexities of Steps 1–3 are O(n), O(1) and O(n), respectively. Afterwards, there are at most n loops in Step 4,and the time complexity of each loop is O(n). Hence, the time complexity of Step 4 is O (n2). Step 5 with time complexity being O(n) will be called for each loop of Step 4.Hence, the total time complexity of Step 4 and Step 5 is O(n2). For Step 6 and Step 7, in each loop of Step 6, it is possible that Step 7 is invoked, and the time complexities are O(n) and O(n2m), respectively. Therefore, the total time complexity of Step 6 and Step 7 is O(n3m). In conclusion, the total time complexity of Algorithm 2 is O(n+1+n+n2+n3m)=O(n3m).

Similarly, with respect to Algorithm 3, the time complexity is O(n2m2). The time complexities of Steps 1–3 are O(m), O(1) and O(m), respectively. For Step 4 and Step 5, the time complexity is O(nm2). In addition, the time complexity of Step 6 and Step 7 is O(n2m2). In a word, the worst-case time complexity of Algorithm 3 is O(n2m2).

Finally, the total worst-case time complexity of Algorithm 1 is O (1+n3m+n2m2)= O (n3m+n2m2).

3.2 Failure of a multi-dispatch task

As mentioned above, when the observation of a multi-dispatch task fails, we do not need to reschedule the failed task because there are other copies and observation opportunities for this task. However, we need to reassign other unscheduled tasks to the released time window, to obtain more observation profits and improve resource utilization. In addition, we need to update the status of the remaining copies because the following copy may become a single-dispatch task due to the failure. Hence, the reactive scheduling policy in this case is described in Algorithm 4.

Algorithm 4Reactive scheduling algorithm (failure of a multi-dispatch task)

Step 1Retract the failed task i from the current schedule C urSol, release the time window resource [wsik,weik] on orbit k.

Step 2Select tasks from the set of unscheduled tasks UnScheTaskSet, and then try to schedule them to the time window [ wsik,weik]. See details in Algorithm 2.

Step 3Update the status of the remaining copies of task i.

Theorem 2The worst-case time complexity of Algorithm 4 isin which n is the number of tasks and m is the number of orbits.

ProofAs shown in the proof of Theorem 1, the time complexity of the first step that releases the time window resource on orbit k is O(1), and the time complexity of Algorithm 2 is O (n3m). Moreover, the time complexity of Step 3 is at most O(m) because there are at most O(m)copies of a multi-dispatch task. Hence, the total time complexity of Algorithm 4 is

3.3 Success of a multi-dispatch task

If a copy of a multi-dispatch task is successfully executed, we retract the other copies of this task, releasing the relevant time windows. Furthermore, we should reschedule the other unscheduled tasks to the released time windows, improving the observation efficiency. In detail,the reactive scheduling policy in this case is described in Algorithm 5.

Algorithm 5Reactive scheduling algorithm (success of a multi-dispatch task)

For each other copy of the successful task i :

Step 1Retract the copy from the current schedule CurSol, and release the relevant time window [ wsik,weik].

Step 2Select tasks from the set of unscheduled tasks UnScheTaskSet, and then try to schedule them to the time window [ wsik,weik]. See details in Algorithm 2.

Theorem 3The worst-case time complexity of Algorithm 5 isin which n is the number of tasks,and m is the number of orbits.

ProofFirst, the time complexity of Step 1 is O(1),and the time complexity of Step 2 is O(n3m) as shown in the proof of Theorem 1. Additionally, Step 1 and Step 2 will be called at most m times because the maximum number of copies of a multi-dispatch task is m. Hence,the total time complexity of Algorithm 5 is O(m·(1+n3m))=O(n3m2).

4. Computational results and analyses

In this section, we provide the results of an extensive simulation study to show the capability of the proposed reactive scheduling approaches under the uncertainties of clouds.

4.1 Experimental layout

In our simulation, the tasks are randomly generated in the following area: latitude 0º– 60º and longitude 0º– 150º.Without loss in generality, the profits of tasks are integers, uniformly distributed over [1,10]. We consider three different satellites with the parameters outlined in Table 2.and the orbit models are obtained from the Satellite Tool Kit (STK). In addition, the memory and energy capacities for each orbit are randomly generated in the intervals[200, 240] and [240, 320], respectively. Considering the uncertainties of clouds, for each observation window, the probability of no blockage of clouds, i.e., the observation is successful, is uniformly distributed in [0.5, 1]. In addition, with respect to the definitions of disruption, the influence degrees of the two categories of disruptions are defined as σ1= 4 and σ2= 1.

Table 2 Parameters of satellites

In this study, all algorithms are coded in C++ and run on a personal laptop computer equipped with an Intel (R)Core (TM) i5-2430M 2.40 GHz (2 processors) and 4 GB RAM.

4.2 Performance evaluation of the reactive scheduling algorithms

In this section, to evaluate the performance of the proposed reactive scheduling algorithms, a number of problem instances are randomly created. In detail, the numbers of tasks are set to 20, 40, 60, 80, 100, and 120. In addition,the scheduling horizons are first set to 12 h and 24 h,which correspond to 21 and 42 orbits, respectively. For each parameter setting, ten problem instances are randomly created. In our previous studies, the baseline schedules are produced by an expectation model [42], a chance-constrained model [2], and a robust optimization model [41].Notably, the performance of the reactive scheduling algorithms depends on the disruptions of the cloud uncertainties, related to concrete scenarios. Hence, to avoid the performance impact of the different scenarios, we create a large sample of 1 000 scenarios for each problem instance. First, we analyze the performance of the reactive scheduling algorithms when the baseline schedules are produced with the expectation model. The experimental results are shown in Fig. 6.

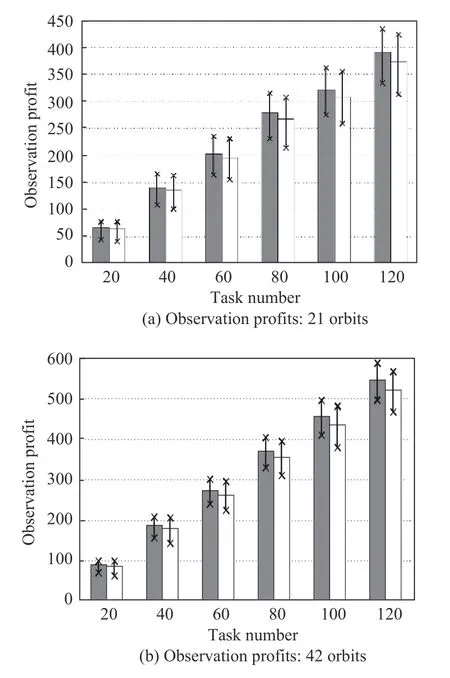
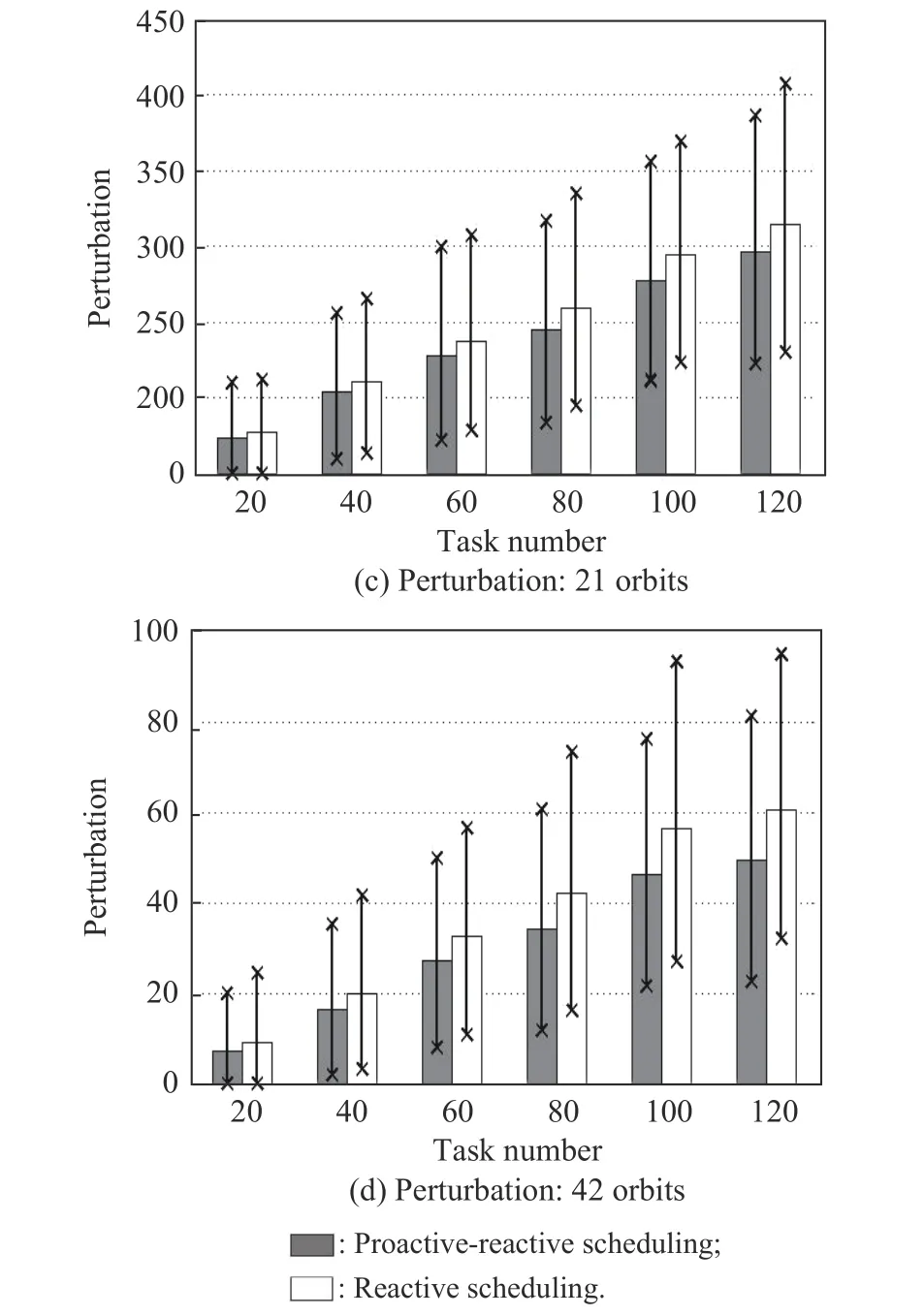
Fig. 6 Performance analysis of reactive scheduling: expectation model

As shown in Fig. 6(a) and Fig. 6(b), the observation profits increase with the increase of the task number. Furthermore, the performance of the proactive-reactive scheduling algorithm is superior to that of the pure proactive scheduling algorithm, regardless of the minimum, average, or maximum values. This is because when the observation fails due to the presence of clouds, the pure proactive scheduling has no reaction, decreasing the observation profits. However, the proactive-reactive scheduling reassigns the failed task to other observation windows,stabilizing the scheduling profits.

Furthermore, as illustrated in Fig. 6(c) and Fig. 6(d),the perturbation increases with the increase of the task number. This can be attributed to the fact that the number of failed tasks increase due to cloud blockage. Although the reactive scheduling is considered, the reschedule also results in variances in observation resource or time. Moreover, from the comparisons, we discover that the reactive scheduling algorithm can reduce the system perturbation. The reason is that the first type of disruption is caused without reactive scheduling, but the reactive scheduling can transform the first type to the second type of disruption. Clearly, the perturbation measurement for the first type is much larger than that of the second type.

Fig. 7 depicts the performance of the reactive scheduling algorithm when the chance-constrained model is adopted for the proactive scheduling. Similar to Fig. 6,Fig. 7(a) and Fig. 7(b) show that the observation profits increase with the increase of the task number and the reactive scheduling can improve the observation profits.Fig. 7(c) shows that the perturbation first increases with the increase of the task number for 21 orbits; however,it decreases from 60 to 80 tasks, and then continues to increase further. In addition, for 42 orbits, the perturbation also starts increasing and then decreases from 100 to 120 tasks, as shown in Fig. 7(d).

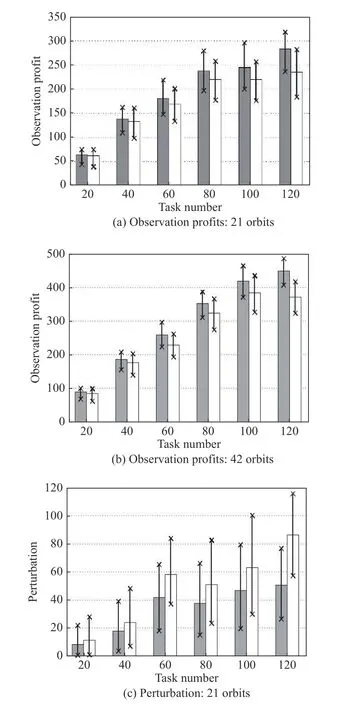
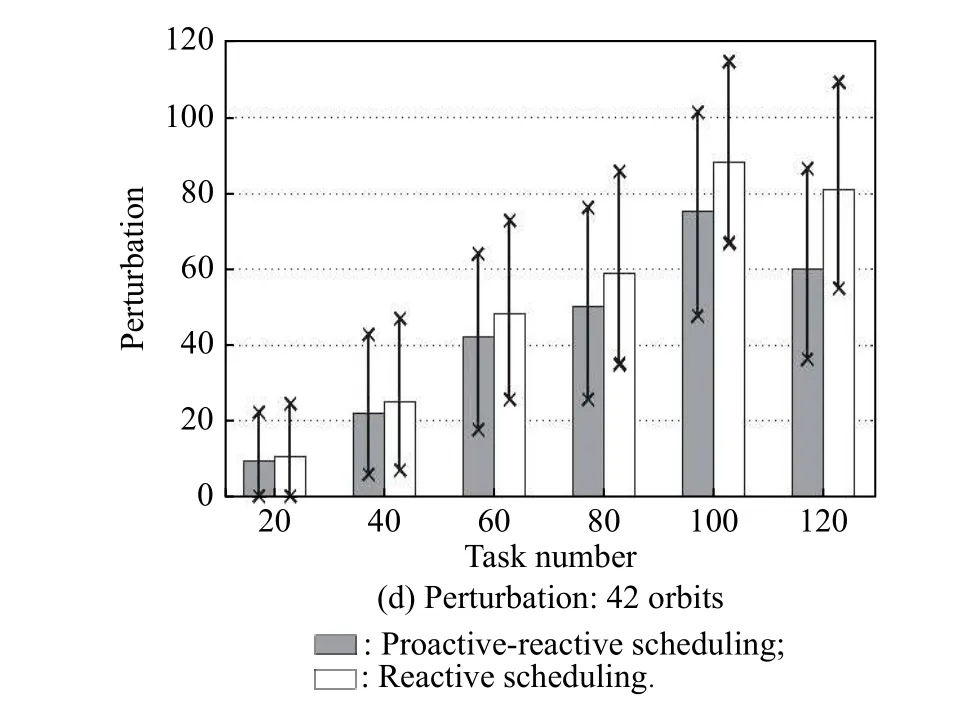
Fig. 7 Performance analysis of reactive scheduling: chance-constrained model

Fig. 8 describes the performance of the reactive scheduling algorithm when the robust optimization model is adopted for the proactive scheduling. Similar to the former experimental results, the reactive scheduling can improve the observation profits. In addition, as shown in Fig. 8(c) and Fig. 8(d), the perturbation increases with the increase of the task number, and the reactive scheduling can decrease the perturbation.

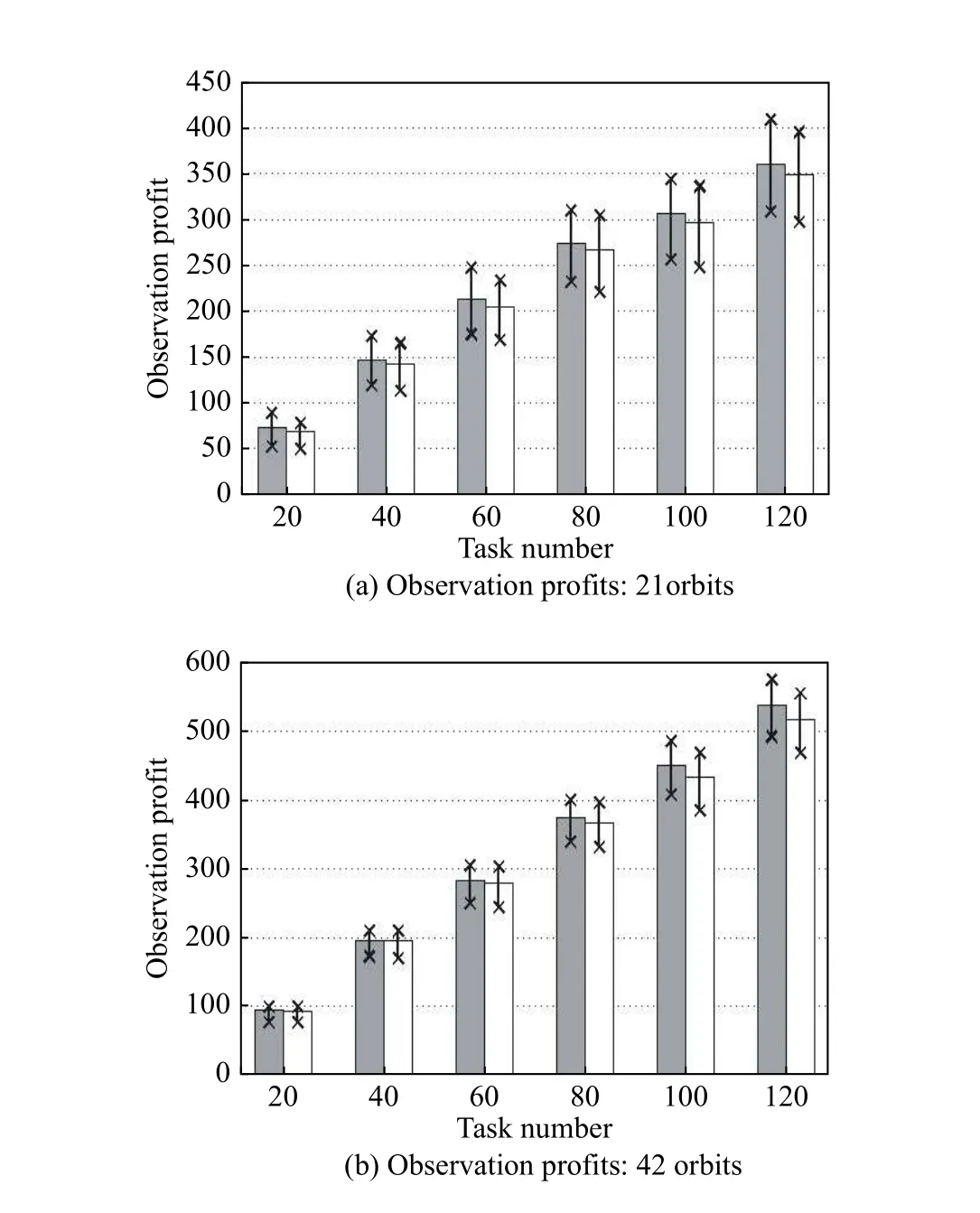
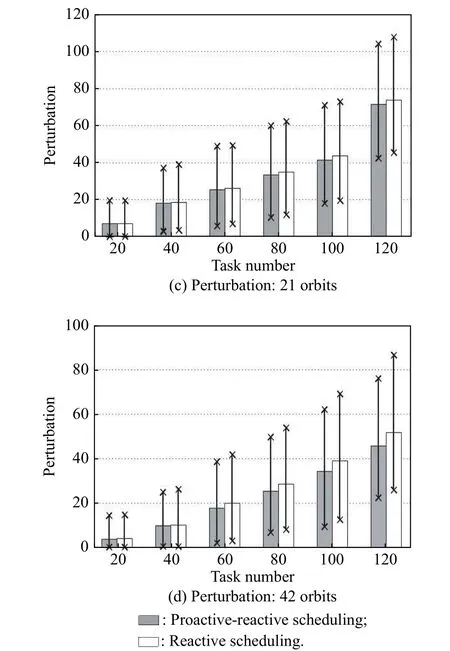
Fig. 8 Performance analysis of reactive scheduling: robust optimization model

4.3 Performance comparisons of the modeling methods for the proactive scheduling

In this section, we analyze the scheduling performance of different modeling methods for the proactive scheduling,such as the expectation, chance-constrained, and robust optimization models, with or without the reactive scheduling. The parameter setting is identical to that in Subsection 4.2, and a sample of 1 000 scenarios is also created for each problem instance.

In Fig. 9, we analyze the scheduling performance of different models for proactive scheduling without reactive scheduling. It is shown in Fig. 9(a) and Fig. 9(b) that the observation profits increase with the increase in the task number for the expectation and robust optimization models, which has been explained in the previous section.With regard to the robust optimization model, the observation profits also initially increase; however, they remain unchanged or decrease with further increase in the task number. In addition, for fewer tasks (20–80), the observation profits of the robust optimization model are larger than those of the expectation model. On the contrary,the observation profits of the expectation model are larger than those of the robust optimization model for a greater number of tasks (100–120). Particularly, the observation profits of the chance-constrained model are always minimal.

As shown in Fig. 9(c) and Fig. 9(d), for the expectation and robust optimization models, the perturbation ascends with the increase of the task number. However,with respect to the chance-constrained model, the perturbation initially ascends, then descends, and finally continues to ascend. Moreover, for 21 orbits, the perturbation of the expectation model is larger than that of the robust optimization model for fewer tasks. This is because we do not consider the robustness in the expectation model, and the baseline schedule lacks an anti-interference capacity. Therefore, the observation of numerous tasks fails due to the presence of clouds, which increases the perturbation. However, for more tasks, the perturbation of the expectation model is smaller than that of the robust optimization model. In addition, for 42 orbits, the perturbation of the robust optimization model is always minimal, whereas the perturbation of the chance-constrained model is always maximal.

Furthermore, with reactive scheduling, we also compare the scheduling performance of the different proactive scheduling models, as shown in Fig. 10. Fig. 10(a) and Fig. 10(b) show that the observation profits of the robust optimization model are larger than those of the expectation model for fewer tasks. This can be attributed to the fact that the robust optimization considers the scheduling robustness, which increases the ratio of task completion and enables more tasks to be completed. However, for more tasks, the observation profits of the robust optimization model are fewer because the multi-dispatch of the robust model increases the system load, which decreases the solution optimality. Although observations may fail due to the presence of clouds for the expectation model,the reactive scheduling can repair the schedule and reassign the failed observations. In addition, the observation profits of the chance-constrained model are always the smallest.

As shown in Fig. 10(c), when the number of tasks is small, the perturbation of the chance-constrained model is the largest, and the perturbation of the robust optimization model is the smallest. The reason is that the robust optimization model has a strong anti-jamming capacity.However, for more tasks, the perturbation of the robust optimization model becomes the largest. In addition, for 42 orbits, the perturbation of the robust optimization model is the smallest, whereas the perturbation of the chance-constrained model is the largest.

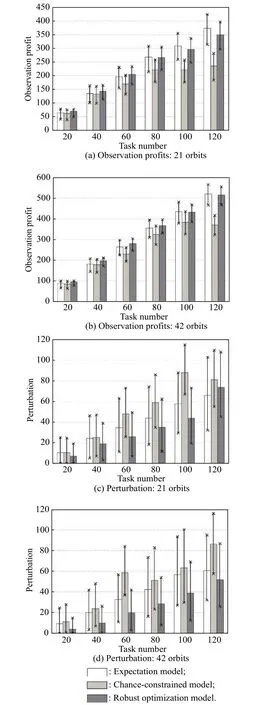
Fig. 9 Performance analysis of modeling methods for proactive scheduling (without reactive scheduling)

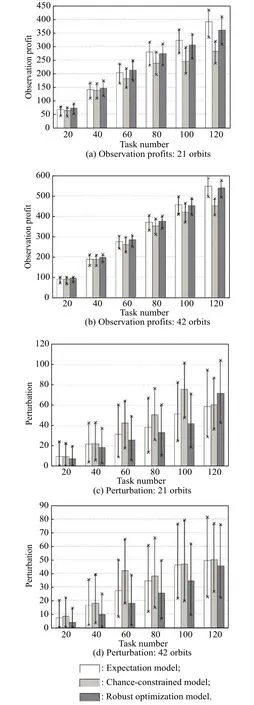
Fig. 10 Performance analysis of modeling methods for proactive scheduling (with reactive scheduling)

4.4 Performance evaluation on large-scale problem instances

In this section, to further verify the effectiveness of the reactive scheduling algorithms, we test the algorithm performance on large-scale problem instances. Specifically,the numbers of tasks are 200, 300 and 400; the numbers of orbits are still 21 and 42. Similar to the previous experiments, for each parameter setting, ten problem instances are randomly created. Therefore, we have 60 instances in total. In addition, the sample size is also set to 1 000 for each problem. Due to the limitation in computer memory,large-scale problems could not be solved by one of the proactive scheduling algorithms [2]. Therefore, in this section, the baseline schedules could only be produced by expectation [42] and robust optimization models [41].

First, we verify the performance of the reactive scheduling algorithms when the baseline schedules are produced by the expectation model. The experimental results are shown in Table 3.

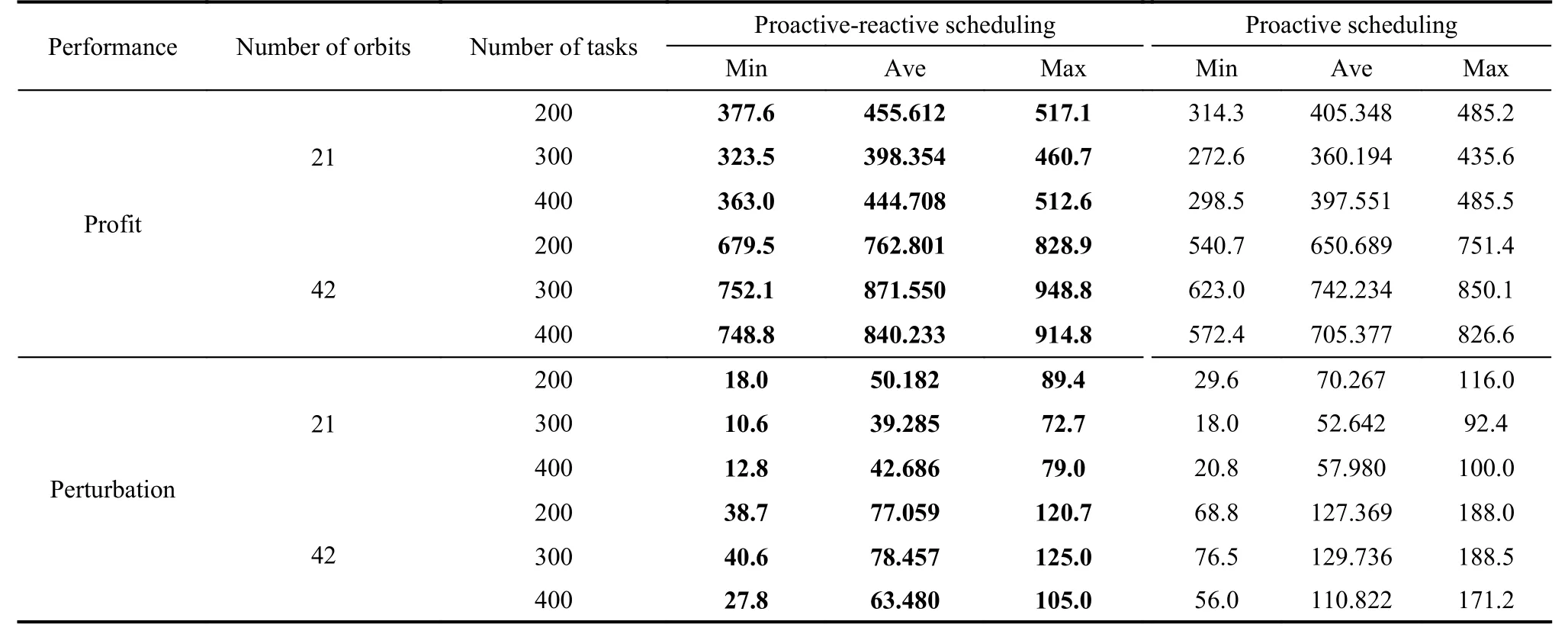
Table 3 Performance analysis on large-scale problem instances: expectation model

Similar to the prior experimental results, the observation profits of the proactive-reactive scheduling algorithm are larger than those of the pure proactive scheduling algorithm, regardless of the minimum, average, or maximum values. Additionally, the reactive scheduling algorithm can also reduce the system perturbation because the reactive scheduling can reduce the number of tasks that fail to be observed (the first type of disruption).

In the following, we also test the effectiveness of the reactive scheduling algorithms when the baseline schedules are produced by the robust model. The experimental results are shown in Table 4.

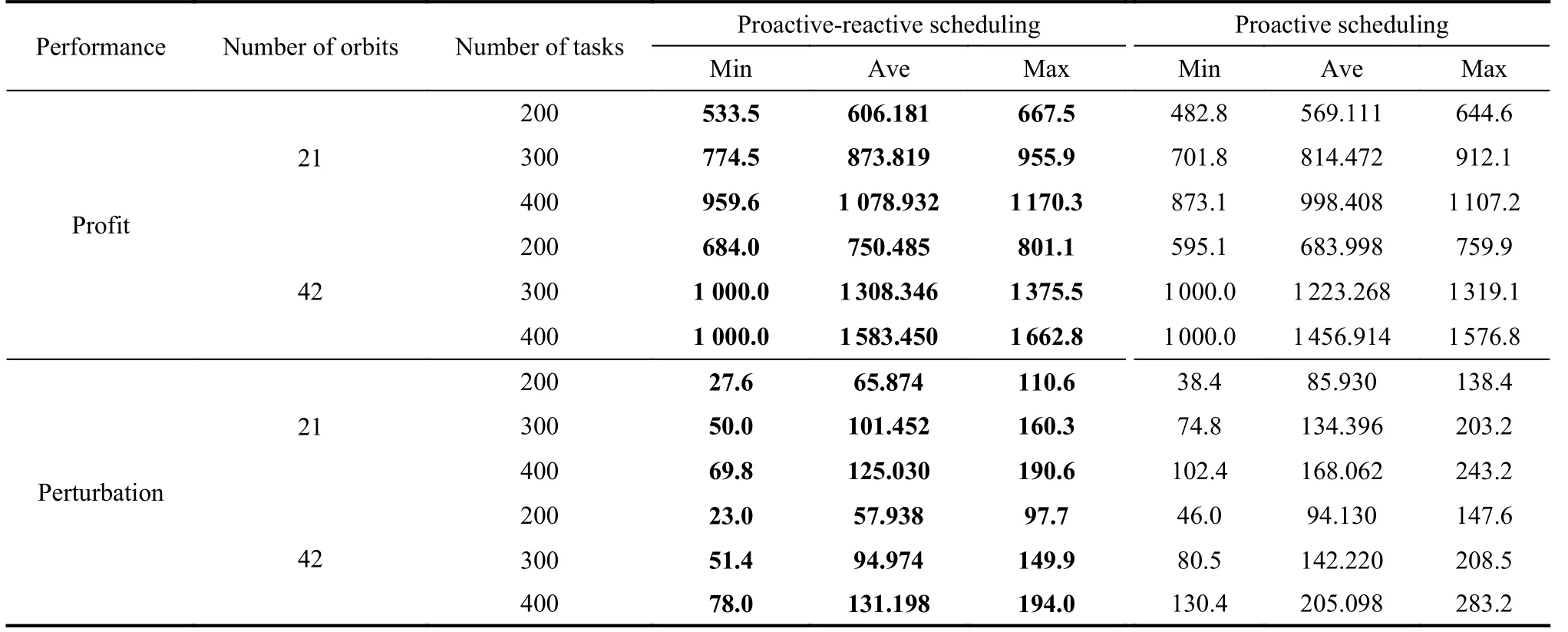
Table 4 Performance analysis on large-scale problem instances: robust model

From the experimental results in Table 4, we can obtain a similar conclusion that the reactive scheduling algorithms in this study can both improve the observation profits and reduce the system perturbations under cloud uncertainties.

5. Conclusions

On the basis of the previous studies on proactive scheduling, we investigate the reactive scheduling problem to further hedge against disruptions due to cloud uncertainties. Initially, we describe the reactive scheduling problem and highlight the significance of the reactive scheduling through a simulated instance. Considering two objectives, the observation profits and the scheduling stability,a multi-objective optimization mathematical model is constructed. Thus, we propose an event-driven reactive scheduling mechanism and obtain the possible disruptions from cloud uncertainties during the execution of the baseline schedule. With regard to different disruptions,different reactive scheduling algorithms are suggested.Finally, a considerable number of simulation experiments are conducted to verify the effectiveness and feasibility of the reactive scheduling algorithms. The experimental results show that reactive scheduling can improve observation profits and also reduce the perturbation, satisfying users’ requirements.

In the future, the scheduling problem of agile EOSs under uncertainties will be considered. Different from nonagile satellites, the scheduling of agile satellites is more flexible due to long time windows for observation. Hence,we need not only allocate the tasks to the orbits, but also decide the start and finish time, which makes the problem more complicated. In addition, we will design more sophisticated algorithms for the reactive scheduling problem to further improve the scheduling performance.