耦合热声网络与激励盘模型预测燃烧室的不稳定振荡
邵卫东,高贤智
(1.中国航发商用航空发动机有限责任公司,200241,上海;2.上海市航空发动机数字孪生重点实验室,200241,上海)
为降低民用航空发动机污染物排放,当前的燃烧室设计一般采用贫油预混分级组织喷雾燃烧技术[1],但其易产生燃烧不稳定性。该现象的物理本质是火焰动力学与声学的双向耦合[2-7],当火焰产生的扰动与燃烧室内声波在火焰处的相位差小于某一定值时,扰动幅值在初期线性增长,如果非线性激励大于非线性阻尼,扰动幅值呈指数增长,从而诱发低频高幅振荡,破坏燃烧室的结构完整性。
对燃烧室构型与气动布局进行优化,可有效规避热声振荡的发生。优化的物理模型即为热声耦合控制方程,当前确定物理解的数值方法有大涡模拟(LES)[8-11]、混合计算流体力学-计算气动声学方法[12-14]、低阶模型[15]3大类:
(1)LES方法能够准确考虑涡波、熵波和声波之间的能量转换与非线性过程,但其对计算资源的需求仍不适用于实际燃烧室优化设计;
(2)混合方法将流动变量分解为平均值与脉动值,并对脉动值采用小扰动假设将控制方程线性化,该方法能极大降低计算量,但燃烧释热源项需要采用LES方法或者统计模型获得;
(3)低阶模型将实际燃烧室离散为若干单元,在单元内考虑声传播的集总特征,将所有单元通过边界匹配条件形成传递矩阵,虽然该方法不能考虑模态间能量转换,但其具有直观的物理过程,计算速度快,关联了燃烧室几何参数,有利于优化设计,故本文采用低阶模型方法。
在预测热声振荡过程中,在燃烧室出口通常给定随频率变化的阻抗边界条件,阻抗边界对于准确评估热声振荡频率至关重要。该边界条件可采用试验方法或跨部件LES方法获得,对于不同的燃烧室工况和涡轮构型该阻抗边界不同,在设计阶段通过反复获得阻抗边界的代价很大。燃烧室出口阻抗反映了声波和熵波在燃烧室与涡轮中传播的综合过程,该边界条件是跨部件物理过程的中间产物。
基于此,本文将燃烧室出口边界作为传递变量,采用跨部件耦合方法来进行热声振荡的研究,下面将从热声网络、激励盘模型、耦合策略、模型验证和应用等方面展开。
1 数值方法
1.1 热声网络
热声网络是预测热声振荡过程低阶模型之一,考虑到一般燃烧室头部等结构尺寸与声波波长的比值在0.025左右,可利用低频近似将燃烧室分为包含直圆/环管单元、声学紧凑单元、火焰模型和边界条件等声学子单元的集合,如图1所示。由于环管单元的周向尺寸远大于其轴向和径向尺寸,易激发起周向模态,头部等结构的周向尺寸较小,周向模态的截止频率相对较高,不易激发起周向模态而以轴向模态为主。通过传递矩阵将单元内与单元间的声场特征联结,形成热声系统方程并转化为特征值问题,即可得到振荡频率及幅值分布。
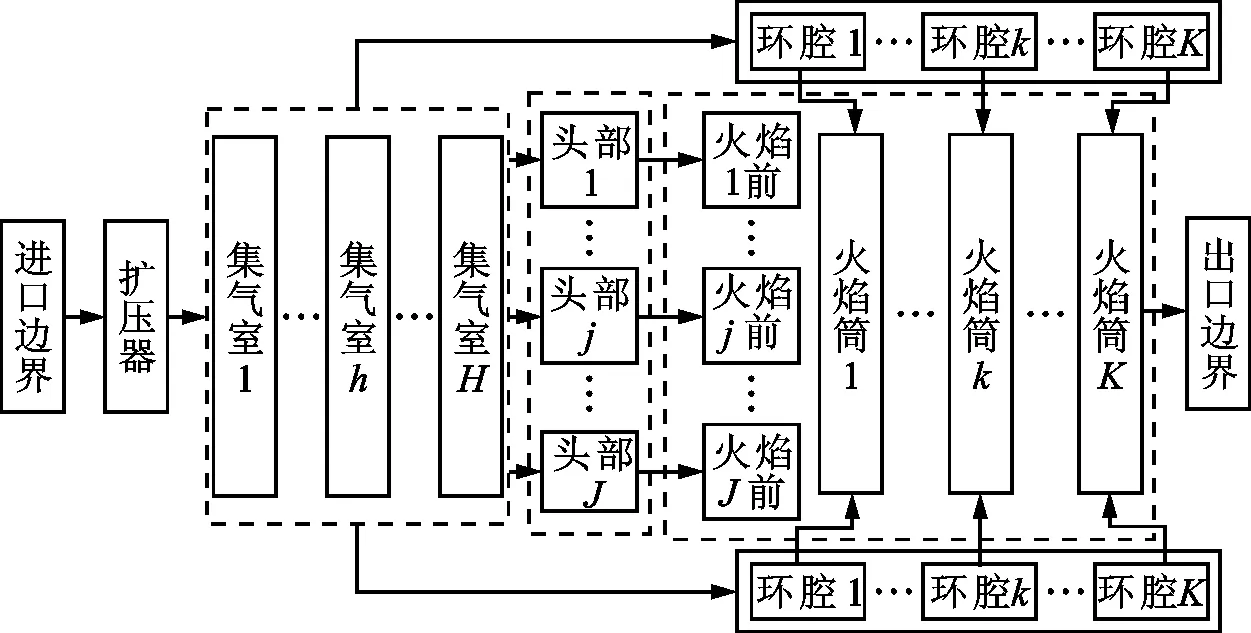
图1 环形燃烧室热声网络示意图
基于理想气体、轴向均匀平均流、无黏、无扩散、小扰动和薄环形假设,将Navier-Stokes方程在柱坐标系下进行线性化处理得
(1)
(2)
(3)
(4)
(5)
式中:(x,θ,R)为柱坐标系;(ux,uθ,uR)为轴向、周向和径向速度;ρ、p和γ分别为密度、压力和比热容比;变量上方横线表示平均值,波浪线表示脉动值。
对于不含释热源的声学子单元,如扩压器、集气室等,联合方程(1)至方程(5)可化简得
(6)
式中:c和Mx分别音速和轴向平均流马赫数。采用分离变量法,方程(6)的解表示为
(7)
(8)
式中:A为待定常数;上标±表示波传播的方向。将式(7)代入方程(2)和方程(3),即可解析轴向与周向脉动速度,利用脉动压力与轴向脉动速度解,轴向相邻声学子单元的声学特征(单模态)可表示为
(9)
(10)
对于周向相邻声学子单元,可采用相似的方法进行声学特征关联,则
(11)
(12)
对于包含释热源的声学子单元如火焰筒,在薄火焰面处对脉动压力和轴向脉动速度利用质量流量和压力连续性条件可得
(13)
式中:xF+和xF-分别表示火焰面位置的两侧;S为声学单元截面的面积;Ω为释热源项,一般采用火焰传递函数[16-18]对其进行模化,则
(14)
其中n表示释热与声波干涉因子,τ表示延迟时间,上标ref表示参考位置。
将所有声学子单元通过传递矩阵连接,即可形成燃烧室热声系统的控制方程
Ax=a
(15)
式中:A为系统特征矩阵;x为系统的脉动变量;a为系统的源项。求解方程(15)对应的特征值问题,可得到振荡频率和振荡模态分布。
1.2 激励盘模型
由于涡轮叶片轴向弦长与声波波长的比值一般低于0.1,叶栅稠度较高且动叶通过频率及其谐波对应的波长远小于发生热声振荡时的声波波长,激励盘模型可利用长波长假设将叶排在轴向简化为无限薄盘片,如图2所示。入射的熵波、涡波和声波进入涡轮级,熵波与涡波全部透射而一部分声波被叶片散射,另一部分声波直接透过叶片通道;熵波与涡波伴随着当地气流速度向下游传播,声波同时向上游与下游传播;通过守恒定律确立盘片上下游脉动量之间的关系。虽然涡轮叶片的轴向弦长较短,但叶排的轴向间距相对于波长不一定可以忽略,故必须考虑熵波、涡波和声波在叶排轴向间隙的传播过程。
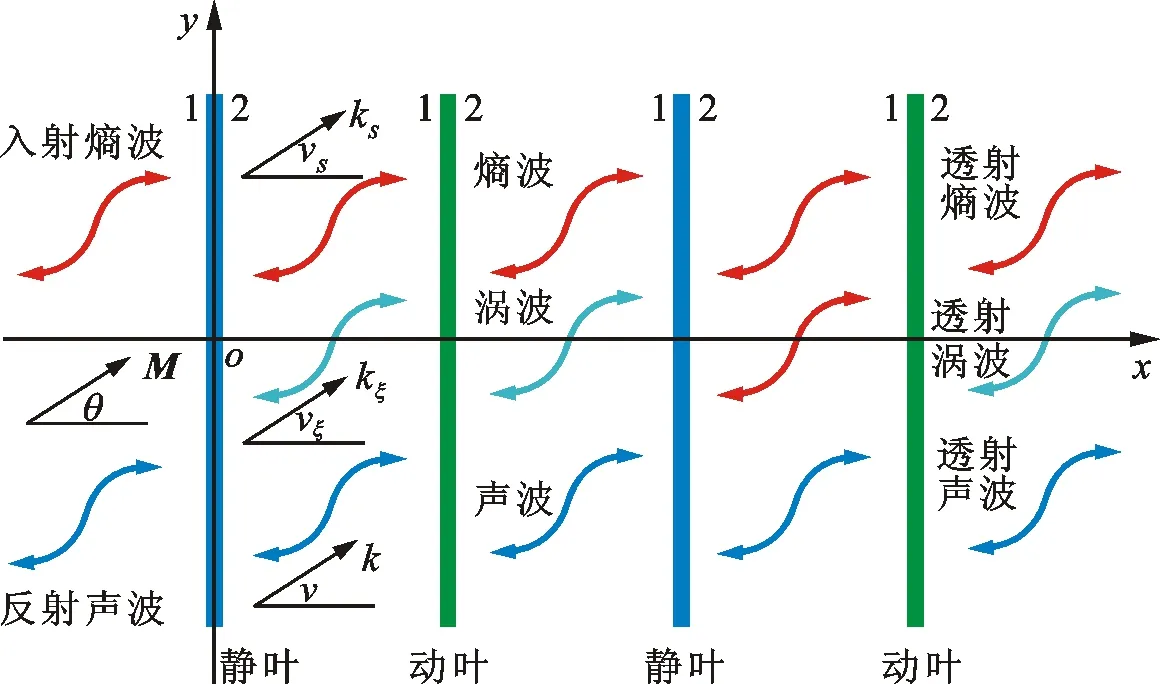
图2 两级涡轮激励盘模型示意图
基于理想气体、均匀平均流、无黏、无热导、长波长、高稠度和忽略叶排内声传播径向变化的假设,将Navier-Stokes方程在二维坐标系下进行线性化处理得
(16)
(17)
(18)
(19)
(20)
式中:(ux,uy)为x和y方向的速度;s为熵。
将熵波、涡波和声波用傅里叶形式表示为
(21)
(22)
(23)
式中:σ、ω、ks、vs分别为熵波幅值、圆频率、熵波数、波数与x轴的夹角,ω=2πf,f为频率;ξ、vξ分别为涡波幅值、涡波数与x轴的夹角;kx、ky分别为声波数k在x与y方向的分量;变量上方尖角表示傅里叶分量。将方程(21)~方程(23)代入方程(16)~方程(19)并整理,可得色散关系为
(24)
(25)
(26)
式中:ca、M、θ分别为声速、马赫数、平均流速度方向与x轴的夹角。
由于熵波不产生伴随的脉动速度与脉动压力,其引起的密度变化为
(27)
涡波不产生伴随的脉动密度和脉动压力,涡脉动速度在平均流方向上的投影和相对于平均流的角度分别为
(28)
(29)
声波引起的密度变化为
(30)
声脉动速度在平均流方向上的投影和相对于平均流的角度分别为
(31)
i(kxx+kyy)]
(32)
由于叶排内脉动具有周期性,熵波、涡波与声波在y方向具有一致波数
ky=kssinvs=kξsinvξ
(33)
对熵守恒、质量守恒和总焓守恒关系进行线性化处理可得
(34)
(35)
(36)
式中:下标1与2分别表示叶排的上游与下游。当叶排出口为亚声速时,满足库塔条件有
(37)
当叶排出口为超声速时,叶片通道内部存在喉口截面,质量守恒关系的线性化形式为
(38)
在单叶排内,可将守恒关系表示成
A1q1=A2q2
(39)
(40)
对于叶片出口为亚声速平均流情形,矩阵A1和A2分别为
(41)
(42)
式中:ζ=[1+M2(γ-1)/2]-1。对于叶片出口为超声速平均流情形,矩阵A1和A2分别为
(43)
(44)
脉动幅值与复合变量q的关系可直接通过式(21)~式(23)进行关联。
对于涡轮级间的声传播过程,上下游叶排间的脉动幅值满足
zu=Tdzd
(45)
(46)
Td=
(47)
式中:|δx|为上下游叶片间距;下标中+、-分别表示声波传播的方向。
将所有叶排通过传递矩阵连接,即可形成涡轮内熵波、涡波和声波传播的控制方程
Bx=b
(48)
式中:B为等价的传播矩阵;x为系统的脉动变量;b为等价的入射波源项。
1.3 耦合策略
在燃烧室与涡轮系统内分别求解方程(15)和方程(48)可得到各自的特征解,在非耦合情形下,方程(15)中矩阵A不能考虑涡轮向燃烧室反射声波的影响,同时方程(48)中矩阵B和向量b不能考虑燃烧室向涡轮入射熵波、涡波和声波的影响。
为求解跨部件系统特征频率,本文引入介于燃烧室与涡轮界面处声阻抗作为过渡变量,通过其在燃烧室与涡轮间进行信息传递,如图3所示。

图3 跨部件耦合计算流程示意图
涡轮进口声阻抗是振荡频率、周向波数、涡轮几何与气动参数的非线性函数,对于给定涡轮集总参数构型,声阻抗可看作只是频率的非线性函数,故涡轮对燃烧不稳定性的影响通过过渡变量间接进入热声系统控制方程(15)中,火焰传递函数的非线性作用直接体现在矩阵A中。
具体计算步骤为:先给定涡轮进口边界条件和假定频率,将这些初边值条件输入到激励盘模型,结合涡轮叶排结构与气动参数计算并装配矩阵B和向量b,得到涡轮进口的前传声波幅值与相位,从而进一步计算得到声阻抗;将声阻抗输入到热声网络模型,结合燃烧室结构与气动参数计算并装配矩阵A和向量a,通过内迭代求解非线性特征值问题得到振荡频率及燃烧室出口相应的熵波、涡波和声波幅值与相位;将得到的振荡频率作为耦合系统外迭代的初始值重复进行直至收敛;判断收敛的依据是外迭代过程相邻两次频率之差不大于10-5,根据测试算例,外迭代过程一般不大于10次即可收敛;耗时模块仍然是求解特征值问题的内迭代过程。
虽然耦合计算模型的总体计算量约为单独热声网络模型计算量的4~7倍,但由于单独热声网络模型计算过程的耗时较短,耦合计算过程的耗时仍是工程实际计算过程可以接受的。
2 结果与讨论
2.1 模型验证
由于跨部件耦合计算相对单独燃烧室热声振荡计算,增加了涡轮激励盘模型,故耦合策略的验证分两步:首先验证激励盘模型的准确性,再验证跨部件耦合计算的准确性,后者主要在下面的应用中进行陈述。
对于激励盘模型的验证,选取Cumpsty的单叶排算例[19],其气动参数如表1所示。

表1 单叶排气动参数
当叶排上游仅有熵波入射时,上游反射声波与下游透射声波随归一化频率的变化关系如图4所示,可见本文的计算结果与Cumpsty的结果吻合较好。由于叶排上游平均流为轴向,y方向上的反射声波模态峰值一致,均出现在截断频率处。由图4b可见,叶片通道内气流加速与折转引起的周向旋流显著改变了y方向上的透射声波。
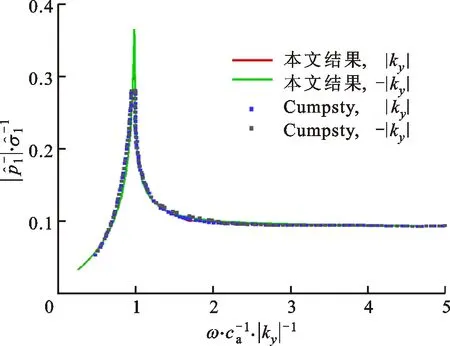
(a)叶排上游反射声波与归一化频率的关系

(b)叶排下游透射声波与归一化频率的关系图4 叶排上游仅熵波入射工况下声波与归一化频率的关系
当叶排上游仅有声波入射时,上游反射声波与下游透射声波随归一化频率的变化关系如图5所示,本文的计算结果与Cumpsty的结果再次吻合较好,验证了激励盘模型的准确性。对于多叶排或多级涡轮的情形,测试结果表明当叶排的个数大于等于3或者涡轮级数大于等于2时,激励盘模型计算得到的涡轮前等效声阻抗已不随叶排的个数而变化。对于多叶排或多级涡轮各分量的独立验证,将在后续的分层仿真规划中考虑。
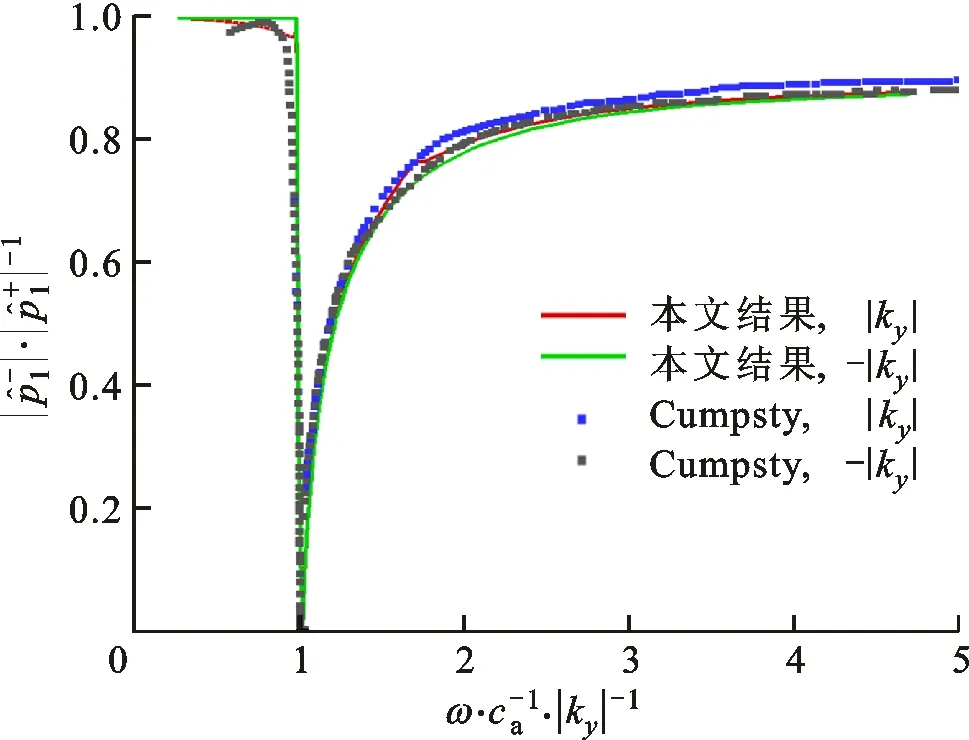
(a)叶排上游反射声波与归一化频率的关系

(b)叶排下游透射声波与归一化频率的关系图5 叶排上游仅声波入射工况下声波与归一化频率的关系
2.2 应用
选取某航空发动机高压涡轮的前两级作为应用算例,其气动参数(气流角在静叶中为绝对值而在动叶中为相对值)如表2所示。
对于涡轮第一级静叶进口和第二级动叶出口,给定边界条件为
(49)
图6给出了振荡频率为400 Hz下等效声阻抗Z(以涡轮进口密度和声速进行归一化)随模态数(以kyRm表示,Rm为涡轮第一级中径)的变化关系,当kyRm=0,±1时,声阻抗变化剧烈,当模态数较大时声阻变化平缓而声抗保持不变。这是因为给定频率下,涡轮内只能激发出3种模态,而大部分高阶模态被截止。
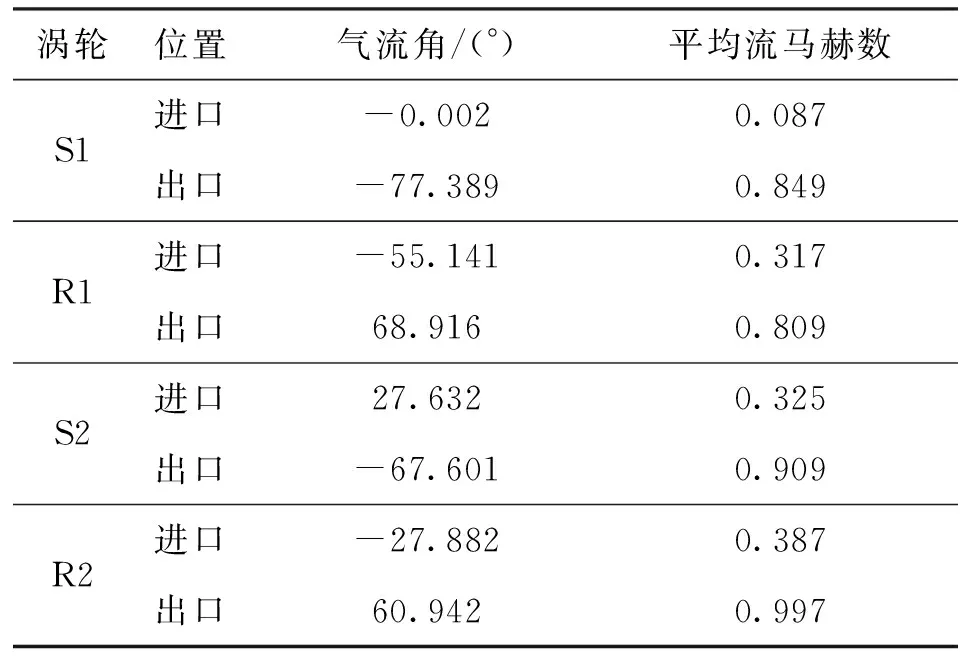
表2 多叶排气动参数
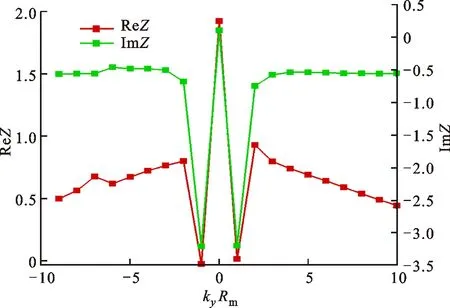
图6 涡轮进口等效声阻抗随模态数的变化
图7给出了给定模态数下涡轮进口等效声阻抗随频率的变化。由图可以看出:不同模态数下声阻抗具有相似的变化规律,声阻随着频率增大而增大,声抗随着频率增大呈现先递减再缓缓增加然后减小的趋势,在250~600 Hz范围内的变化梯度较小,而该频率范围包含热声振荡发生的频率区间。
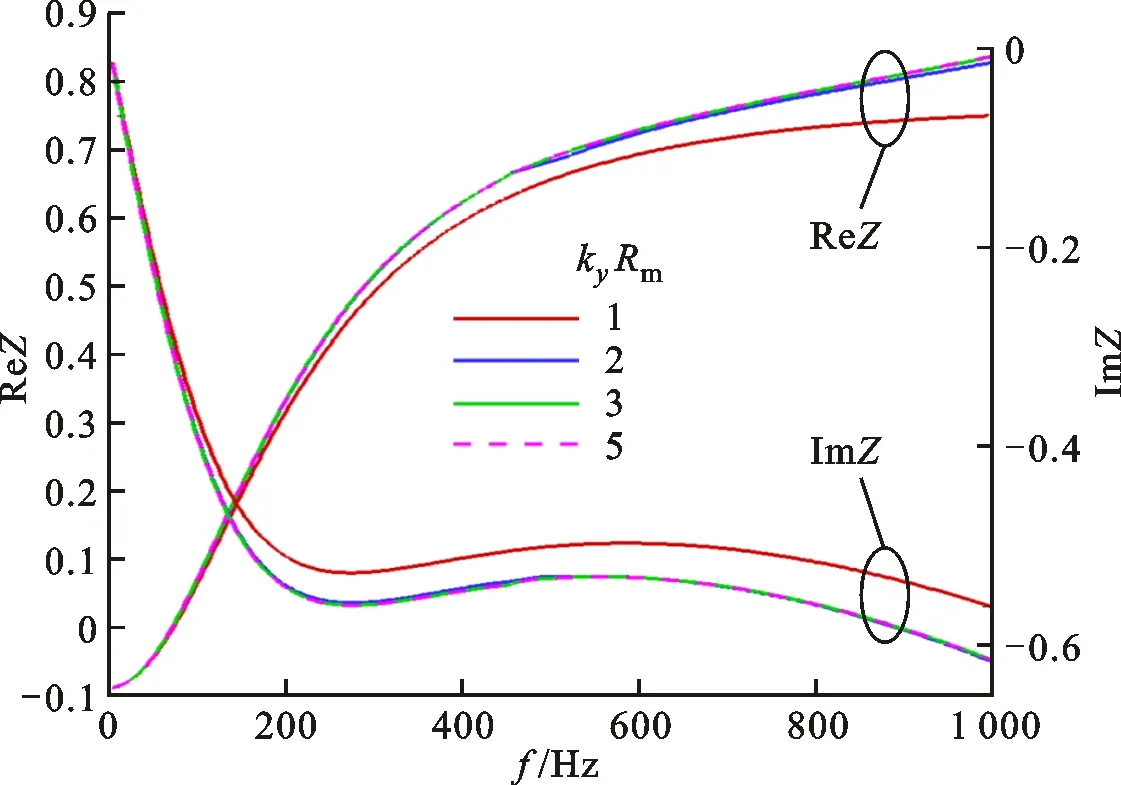
图7 涡轮进口等效声阻抗随频率的变化
对于真实的燃烧室,化学反应放热使得燃烧室内温度梯度较大,对比声学网络模型计算得到的燃烧室出口声波幅值和熵波幅值,发现燃烧室出口熵波幅值一般为声波幅值的1~30倍。
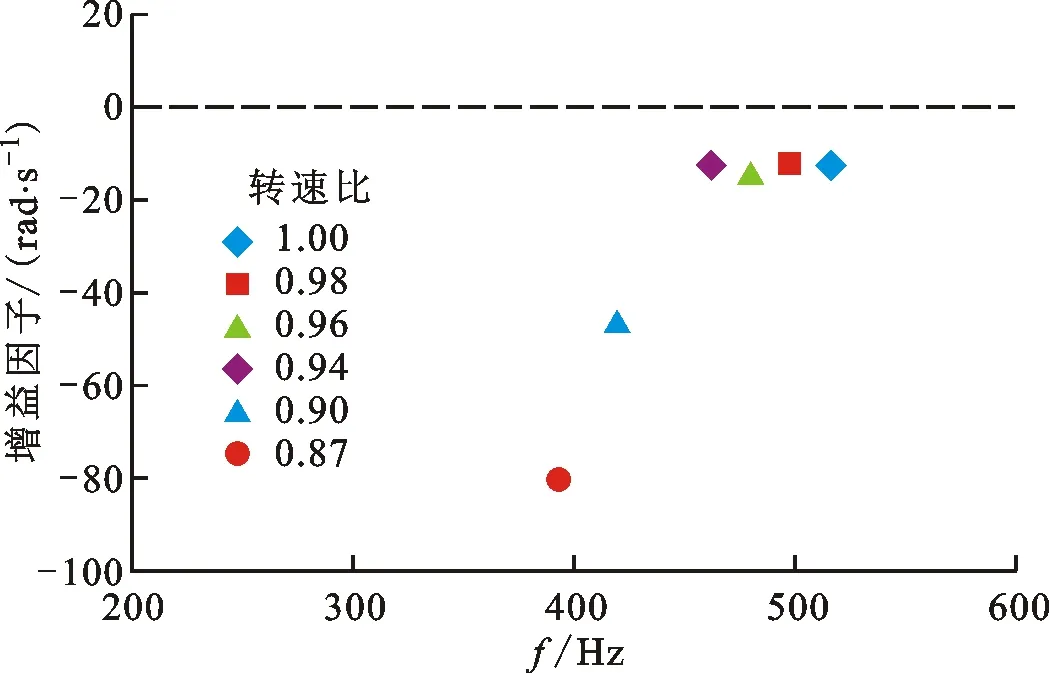
(a)单独热声网络模型结合无反射边界条件 计算所得增益因子与频率分布

(b)单独热声网络模型结合全反射边界条件 计算所得增益因子与频率分布
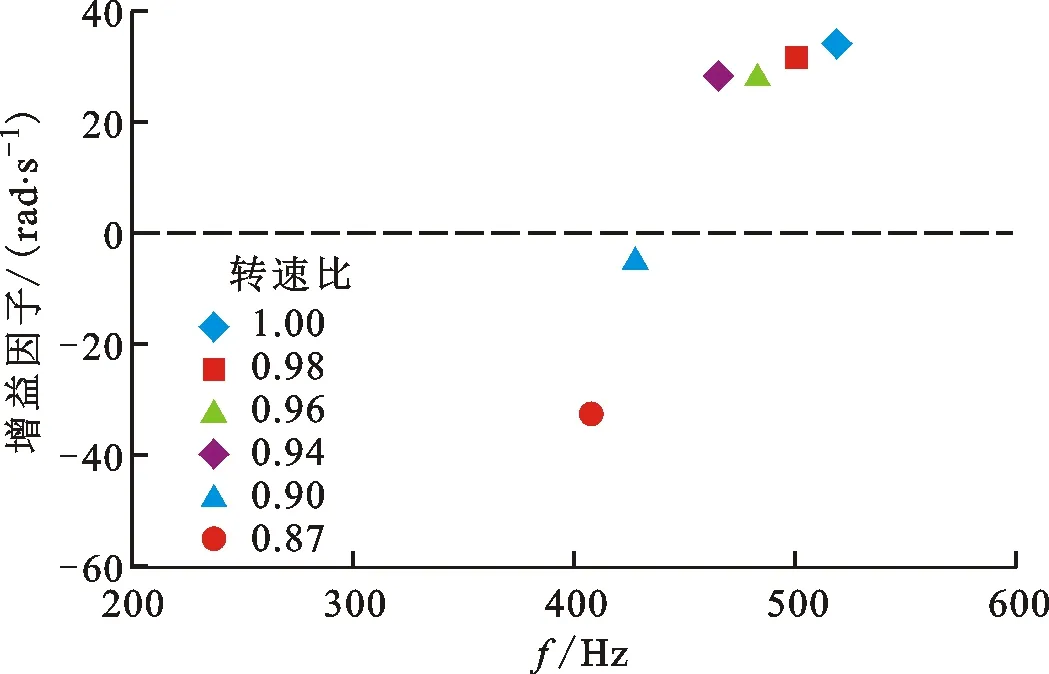
(c)单独热声网络模型结合一维平面波方程导出 阻抗边界条件计算所得增益因子与频率分布
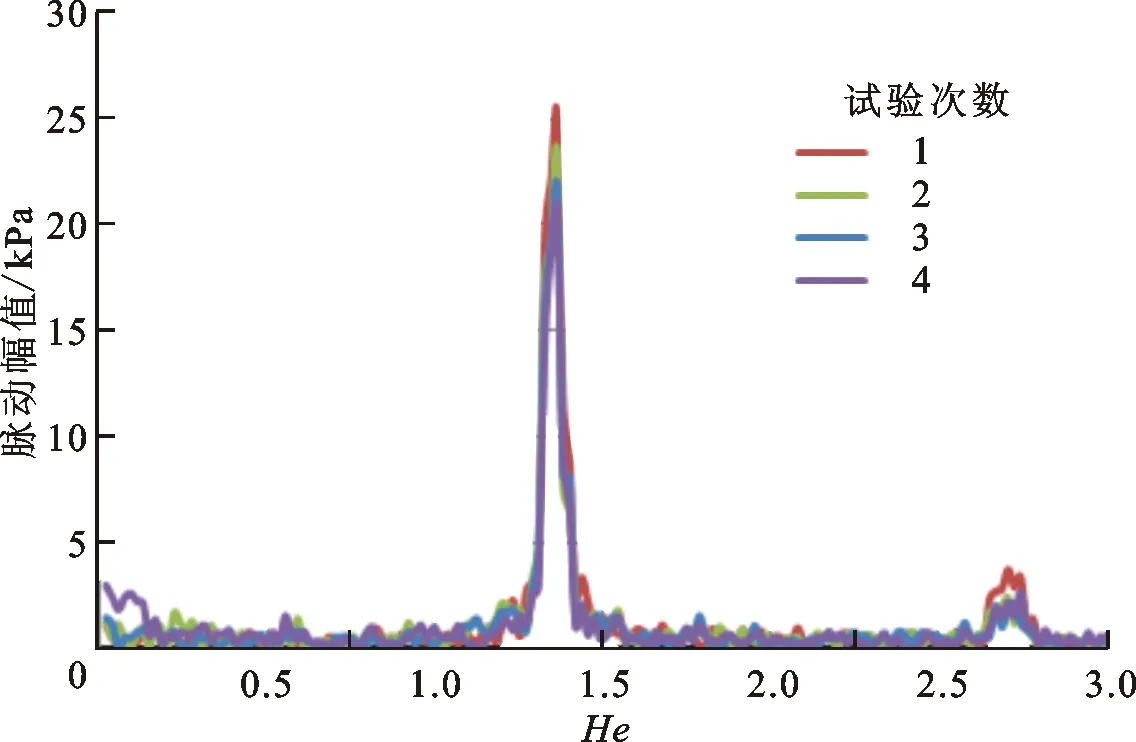
(d)耦合热声网络模型与激励盘模型计算 所得频谱分布图8 燃烧室发生热声振荡下的频谱分布
在较小熵波幅值下,传统的热声网络模型预测热声振荡需要在燃烧室出口给定边界条件,通常有无反射边界条件、全反射边界条件和基于一维平面波方程得到的阻抗边界条件3种方式。不同转速比(核心机转速与额定转速之比)下单独的热声网络模型结合3类边界条件的预测结果如图8a~8c所示,其中无反射边界条件无法判定热声振荡过程的发生,全反射边界条件判定所有工况均发生热声振荡,第3类边界条件发生热声振荡的频率对应的亥姆霍兹数He(He=ωRm/ca)为1.02,而试验测得热声振荡的亥姆霍兹数为1.36,误差为25%。
耦合计算获得的亥姆霍兹数如图8d所示,其中发生热声振荡的频率对应的He为1.36,该值与试验结果相同,二者的一致性证明了耦合计算模型的可靠性。图9给出了特征频率所对应的振荡模态,可见该模态近似为周向负一阶模态,但该模态波节和波节之间的相位差略小于180°。
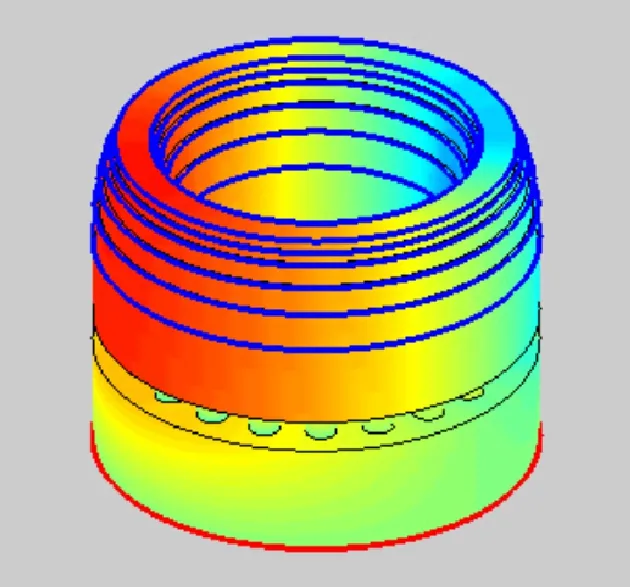
图9 特征频率所对应的振荡模态
图10和图11分别给出了振荡频率下归一化声波和熵波幅值A+、Ae随周向模态数的变化。当周向模态数为-1时,声波和熵波的幅值达到最大,而其他模态数下幅值均可忽略,周向模态数为-1时的熵波幅值大约为声波幅值的20倍。
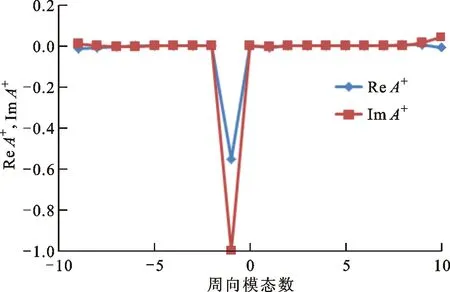
图10 燃烧室出口归一化声波幅值随周向模态数的变化
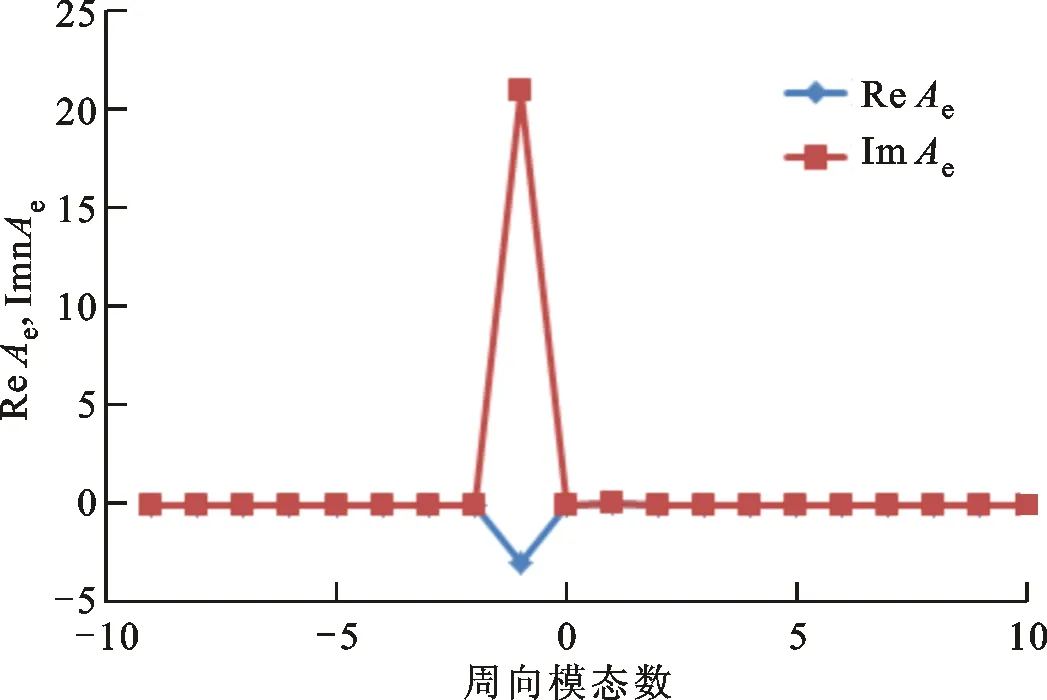
图11 燃烧室出口归一化熵波幅值随周向模态数的变化
图12给出了振荡频率下的等效声阻抗随周向模态数的变化,与图6中各模态下声波和熵波均匀入射情形不同,真实燃烧室出口声波和熵波入射条件下等效声阻抗随周向模态数呈非对称特征,当周向模态数为2时声阻最大而声抗最小,当周向模态数为-1时声阻次大而声抗次小。这说明燃烧室热声振荡主要受到周向正二阶模态和周向负一阶模态的影响,也是图9中模态不完全对称的原因。

图12 燃烧室出口等效声阻抗随周向模态数的变化
值得一提的是,当激励盘入射熵波幅值远大于声波幅值时,耦合求解无法获得振荡频率。可能的原因是入射熵波在撞击到涡轮S1叶片前缘时发生散射并在后续叶排间传播时发生耗散,从而熵波与声波间发生能量转换。本研究未考虑入射熵波的散射和耗散效应,在下一步的工作中将考虑该影响。
3 结 论
本文针对航空发动机燃烧室热声振荡预测中实际出口阻抗边界不定问题,提出了跨部件耦合计算策略,引入燃烧室与涡轮界面处声阻抗作为传递变量,在求解过程中增加了系统间的外迭代。通过经典算例和工程算例的验证,相对于单独燃烧室热声计算,跨部件耦合计算方法能够给出准确的振荡频率和模态分布,该方法可进一步推广至高精度热声预测模型。

