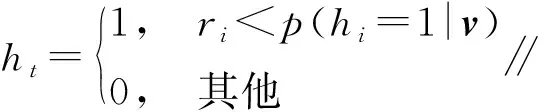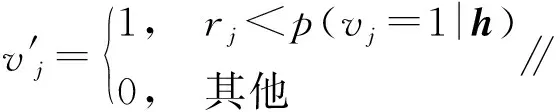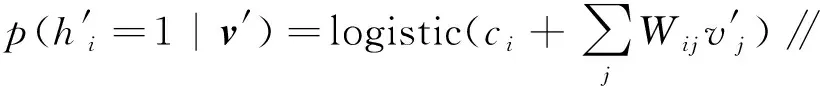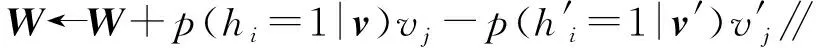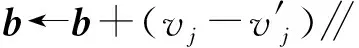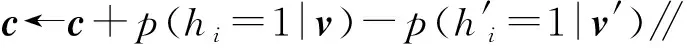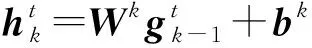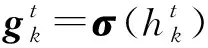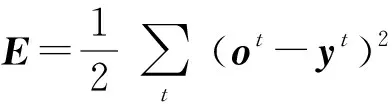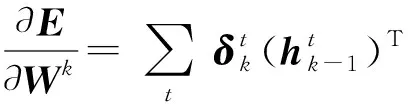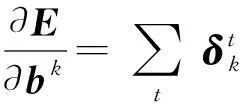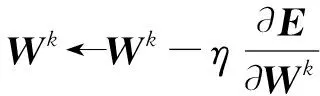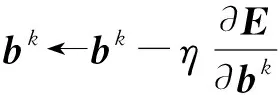深度信念网络在水火电力系统一次调频能力预测中的应用
崔伟,李武璟,王聪,薛晨,段建东,魏嵬
(1.国家电网公司西北分部,710048,西安;2.西安理工大学电气工程学院,710048,西安;3.西安理工大学计算机科学与工程学院,710048,西安)
频率是电力系统安全运行的重要的参数之一,频率的大幅度变化会对整个电力系统的安全稳定运行带来严重的危害。因此,把系统频率控制在允许的正常范围内是电力系统安全稳定运行的前提条件。目前,电力系统的频率调节机制主要由惯性响应、一次调频、二次调频构成。其中,发电机自发进行的一次调频,在频率超出正常范围内会自动调节发电机组的输出有功功率,从而将频率控制在正常范围内。在突发性的频率事件中,一次调频能起到应急作用,为调度人员的二次调频决策争取时间窗口。但是,在频率事故发展迅速的情况下,调度人员很难在短时间内做出正确的判断,评估一次调频能否应对当前频率事件,继而决定是否进行二次调频干涉。因此,需要评估电力系统一次调频能力,在发生频率事件时为调控中心提供辅助决策作用。
从机理上而言,电力系统一次调频能力主要取决于系统中各机组的投运状态、参数设置等。随着智能电网的发展,每台机组的运行状态、参数设置等都进行了测量,相关参数获取更加容易,但各机组的运行状态各不相同,调度人员很难在短时间内准确地分析出电网调频情况并及时决策。因此,需要对电力系统一次调频能力进行预测,辅助调度人员可以在发生扰动时进行紧急控制。
目前,关于一次调频方面的研究主要集中在性能评估[1-2]、特性分析[3-5]和控制策略[6-8]上,主要研究一次调频的各种评价指标、静态特性与动态特性、控制优化等,而对于调频能力本身的研究则关注较少。一次调频能力本身的研究主要分为机组的一次调频能力和电力系统的一次调频能力两类。对于机组的一次调频能力的研究,文献[9]基于同步测量装置的信息,通过实时同步测量机组出力和频率变化,在线测算一次调频相关参数,评估发电机的一次调频性能。然而,现今电网规模增大,发电机组数量众多,每个机组的调频能力与自身的设置参数和运行状态有关,无法快速准确获得整个电网的调频能力。因此,众多学者对电力系统的一次调频能力展开广泛研究。文献[10]定义了电网的一次调频能力,结合方差提出了衡量电网一次调频能力的指标,分析了在线估计的计算可能性;文献[11]考虑调频死区,提出利用均方差定义的电网一次调频能力评价指标;文献[12]基于广域相量测量系统中机组的历史数据,结合时间维度和频差维度,得到电网中单机的一次调频能力预测值,并综合电网中所有单机的预测值,得到电网的一次调频能力预测值,该文是一次调频能力预测方面为数不多的探索,但主要按照固定频差进行预测,预测精度受到制约,且在单机预测的基础上预测电网调频能力计算量会很大。
随着人工智能特别是深度学习的发展,各种基于机器学习的方法已经开始应用于电力系统中[13-15]。电力系统作为一个复杂且高度非线性的系统,含有丰富的特征信息,广泛布置的数据采集与监视控制系统可以为机器学习算法提供大量数据,为模型训练提供样本支撑,构成海量数据集。深度学习算法相较于传统的神经网络算法,具有更加强大的特征提取能力,可以挖掘数据间的深层联系,特别适用于电力系统中海量数据的处理。近些年,电力系统中逐渐应用深度学习算法,尤其是深度信念网络(DBN)。文献[16]应用深度信念网络对电力系统扰动后频率曲线进行预测,结果表明,深度信念网络相较于其他浅层网络更有优势;文献[17]应用深度信念网络对电力系统进行暂态稳定评估预测,结果表明,深度信念网络相较于常规网络具有更高的准确率。深度信念网络采用逐层训练的方式,解决了深层神经网络存在的参数优化问题,为整个网络赋予了较好的初始权值,最后网络只要经过微调就可以获得优秀的参数。深度信念网络结构灵活,易于拓展,对时序数据的预测精度更高[18]。
综合以上考虑,为了准确预测电力系统一次调频能力,为电网调度提供信息支撑,本文探索深度神经网络在电力系统一次调频能力预测中的应用,设计了一种基于深度信念网络的水火电网一次调频能力预测的方法,构建基于深度信念网络的水火电力系统一次调频能力预测模型。选取系统频率、负荷水平、有功负荷、功率缺额、事件类型、发电机组惯性时间常数、备用容量与总备用容量作为预测模型的输入特征值,通过无监督预训练与有监督微调训练网络模型参数,预测60 s的系统功率补偿量变化曲线。通过新英格兰10机39节点系统和某电力公司历史数据作为仿真算例,验证本文所提方法在电力系统一次调频能力预测上的准确性与有效性。本文方法可为频率事件发生后的调度控制提供参考依据。
1 问题描述
电网的一次调频能力是指发生频率事件后系统不依赖二次调频,能自发调整功率的能力。电网调节功率主要通过发电机调速系统调节机组出力,从而调节电网系统功率。因此,可以使用所有机组动态出力变化量之和,即功率补偿量曲线反映系统的一次调频能力。在参与一次调频时,功率补偿曲线会在短时间内快速调节,以尽早消除不平衡功率,然后逐渐趋于稳定值,使得系统达到新的平衡状态。调频效果好时,功率补偿曲线会很快接近或超过功率缺额,消除系统不平衡功率,接着开始趋于稳定,重新运行在新的状态。由于电网一次调频的动作时间一般小于60 s,所以本文采用60 s的功率补偿量变化曲线表征电网一次调频能力,通过分析功率补偿量曲线的稳态值与最大补偿量两种特征,表征电网对于频率事件的最终调节能力与快速反应能力。
机组的相关参数、扰动事件的信息、电网的运行状态均会影响功率补偿量曲线,为了准确预测功率补偿量曲线,需要筛选出3种因素中的主要影响变量。
发生频率事件时,机组调速系统会改变原动机阀门,增加或减少进气量或进水量,导致机组转速发生变化,从而调整机组出力。机组的转速和输入、输出有功功率的平衡有关联。发电机转子运动方程为
(1)
式中:Tj为发电机惯性时间常数;Pm为机械功率;Pe为电磁功率;D为发电机阻尼系数;ω为角频率。
电网是动态变化的多机系统,其动态方程可由系统惯性中心频率和发电机转子运动方程推导而来
(2)
(3)
式中:ωCOI为惯性中心频率;Tj,sys为所有机组的惯性时间常数之和;Pmi与Pei分别为第i台机组的机械功率与电磁功率。
从式(1)(3)可以看出,发电机惯性时间常数直接影响机组转速,进而影响机组功率调节曲线。在其他参数不变的情况下,机组惯性时间越大,则转子转速变化率越小,机组的功率调节速度越慢。
除了惯性时间常数,发电机组的备用容量同样影响机组的功率调节曲线。在频率事件中,不同备用容量的发电机调频能力不同,对于不平衡功率的消纳程度相异。备用容量公式为
(4)
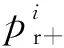
在机组参数方面,主要影响变量为各机组惯性时间常数、备用容量与系统所有机组的总备用容量。
扰动事件主要分为高频扰动与低频扰动两种,两种事件类型的功率调节曲线趋势相反。电网中发电机组对于高频事件与低频事件的调频性能存在差异,文中使用+1与-1分别表示高频事件与低频事件。系统功率缺额为系统发电机组总发出的有功功率与系统总消耗的有功功率的差值,而不同强弱程度的扰动导致机组发出的有功功率、负荷消耗的有功功率或联络线交换的有功功率发生变化,从而产生的功率缺额也不同,使得功率调节曲线存在差异。因此,从扰动事件方面考虑,主要影响变量为事件类型、功率缺额。
对于相同的机组参数与扰动信息、不同的运行状态,由于电网的状态参数不同,频率事件的响应存在差异,因此功率调节曲线不同。电网运行状态考虑系统的频率、负荷水平、有功负荷这3种主要影响变量。
因此,对电力系统调频能力的预测需要结合机组的参数设置、电网的运行状态与事件的扰动程度这3种因素,建立主要影响变量与功率调节响应之间的关系。选取影响电网一次调频能力的8个主要变量作为输入特征量,分别是:事件类型,扰动后功率缺额,扰动后机组备用容量,扰动后系统总备用容量,扰动后机组惯性常数,扰动前系统频率,扰动前负荷水平,扰动后有功负荷。
该问题本质为一个高维的回归问题,将事件类型、系统频率、负荷水平、有功负荷、功率缺额、发电机组惯性时间常数、备用容量与总备用容量作为模型的输入量S,60 s的功率补偿量曲线作为输出量P,实质为求解输入S与输出P的映射关系。输入集与输出集可描述为
(5)
式中下标i表示样本的数量。输入数据集S中任一元素si均为一个行向量,向量中所有元素均为某一样本的输入特征量,即系统频率、负荷水平、有功负荷、功率缺额、发电机组惯性时间常数、备用容量与总备用容量。输出数据集P中任一元素pi同样为行向量,向量中每一个元素对应某一样本的60 s的功率补偿量变化值。
对于该类问题,深度学习可以通过多层非线性处理层对海量数据进行提取与转换,充分挖掘数据间的联系。深度信念网络可通过无监督预训练与有监督参数微调相结合的训练方式获得优秀的权值,相较于其他深度神经网络结构灵活,对处理时序数据更具有优势。
2 基于深度信念网络的预测网络模型
2.1 深度信念网络简介
Hinton在文献[19]中首次提出深度信念网络,该网络由多层受限玻尔兹曼机(RBM)堆叠而成。标准RBM由输入层与隐藏层组成,同层节点之间无连接,不同层节点之间相互连接。标准RBM的结构如图1所示。
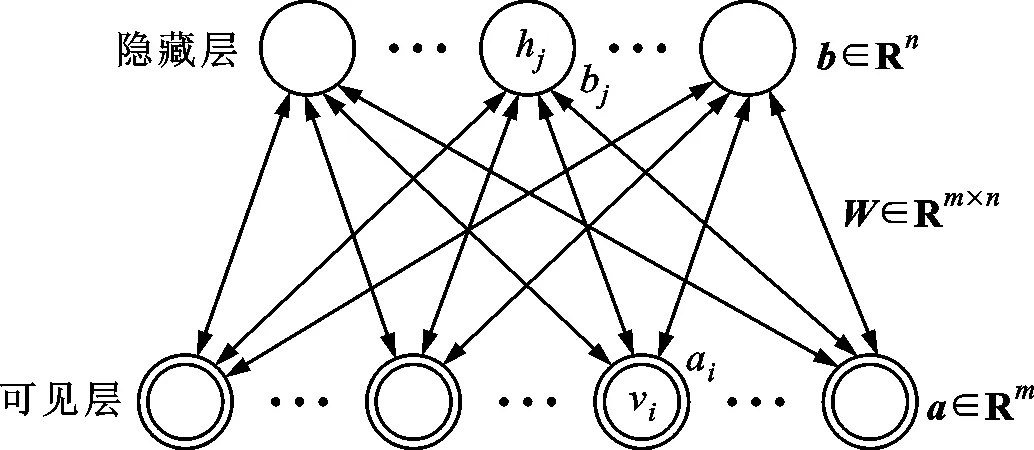
vi—可见层第i个神经元;hj—隐藏层第j个神经元;ai—vi的偏置;bj—hj的偏置;a—输入层偏置矩阵;b—输出层偏置矩阵;W—权值矩阵。图1 标准RBM结构
设RBM可见层有m个神经元,隐藏层有n个神经元,神经元vi与hj均为二值变量,取值为0或1。某一状态下RBM结构的能量函数公式[19]为
(6)
式中:θ={Wij,ai,bj,1≤i≤m,1≤j≤n};Wij为可见层神经元vi与隐藏层神经元hj之间的权值。根据能量函数可得RBM的联合概率分布为
(7)
式中Z(θ)为配分函数,即所有状态下RBM结构的能量函数。
深度信念网络的训练将预训练与参数微调结合,包含无监督预训练与有监督参数微调两部分。深度信念网络的训练方法如图2所示。
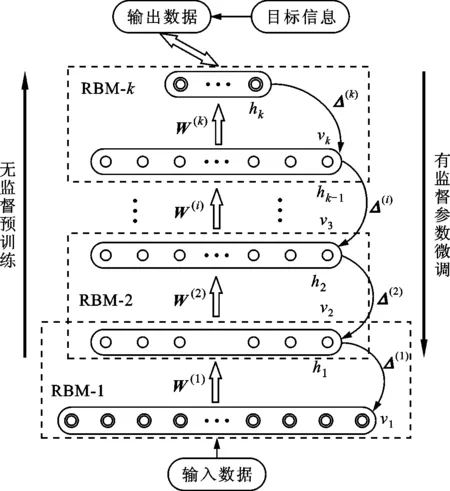
Δ(i)—b和W的调整矩阵。图2 深度信念网络训练方法[20]
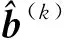
2.2 基于深度信念网络的电网一次调频能力预测方法设计
2.2.1 模型结构设计 标准的深度信念网络常用于分类,无法满足一次调频能力预测的需求,因此本文所用DBN的输出层采用线性传递函数,从而使DBN具备处理回归问题的能力。本文设计的DBN结构如图3所示。
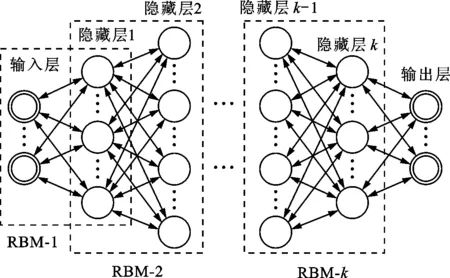
图3 深度信念神经网络结构
2.2.2 模型训练方法 DBN网络训练包括无监督预训练与有监督参数微调两部分,其中无监督预训练采用对比散度算法,有监督参数微调采用梯度下降算法。在无监督预训练阶段,将非最高层的每相邻两层看做一个RBM进行对比散度算法训练,获得较好的参数初值,伪代码见附录A。无监督预训练完后,将整个神经网络作为普通的反向传播神经网络,通过梯度下降算法从高到低对参数进行微调,使得DBN得到最优的参数,伪代码见附录B。
2.2.3 评价指标 本文采用平均相对误差和均方根误差来评价模型性能的优劣,二者公式为
(8)
(9)

3 仿真算例
3.1 新英格兰39节点系统仿真算例
3.1.1 算例系统介绍 新英格兰39节点系统包括10台发电机、12台变压器、39条母线、34条线路[21]。该系统为美国新英格兰州的一个345 kV电力网络,基准功率为100 MW,基准电压为345 kV,额定频率为60 Hz。新英格兰10机39节点系统接线图如图4所示。
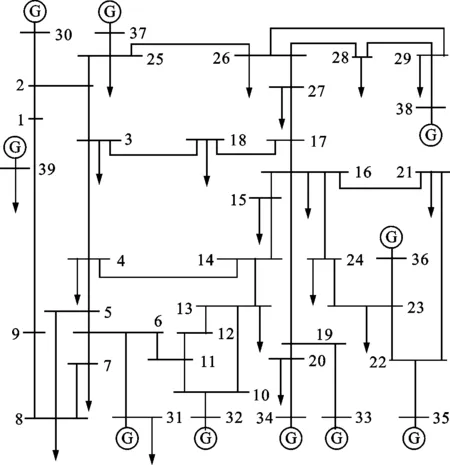
—发电机;1~39—系统节点母线。图4 新英格兰10机39节点系统接线图
仿真软件采用PSASP,模拟扰动类型主要为切机扰动和负荷突变,分别生成高频事件数据与低频事件数据。系统的扰动数据生成过程如下。
(1)根据文献[21]中新英格兰10机39节点系统的负荷、线路、变压器、发电机、调速器与励磁系统的参数数据,使用PSASP软件对系统进行建模。
(2)通过设置各种扰动故障,进行暂态稳定仿真分析,获取所需样本初始数据。对初始数据进行处理,获得预测模型所需要的输入特征数据与对应的60 s内系统功率补偿量。根据文献[16]的扰动设置方法,本文设置31%、32%、……、80%共50种负荷水平,1、0.75、0.5、0.25共4种机组惯性时间常数。低频扰动事件数据通过在同一负荷水平、惯性时间常数下,轮流切除1台发电机,共获得2 000组仿真样本数据。高频扰动事件数据同样在同一负荷水平、惯性时间常数下,每次负荷骤降10%、15%、……、55%,共获得2 000组仿真样本数据。仿真设置在0.1 s时发生扰动故障,时长为60 s,总共生成4 000组样本。
(3)对样本数据进行归一化处理,使用MATLAB软件中的mapminmax函数将数据归一化至0~1之间。
(4)将处理后的数据集随机划分为训练集与测试集。对于高频扰动事件与低频扰动事件,均选取1 500组和500组样本作为训练和测试样本。
3.1.2 模型参数分析 为预测电网一次调频能力,将模型输出设置为扰动后60 s的功率补偿量曲线,故输出神经元数设置为60。输入特征为第1节所述的各机组惯性时间常数、备用容量、系统所有机组的总备用容量、事件类型、功率缺额、系统频率、负荷水平和有功负荷,在新英格兰39节点中对应26个输入神经元。对于隐藏层层数与隐藏层神经元数,在隐藏层最多为5层的限制下进行多次尝试,获得合适的参数。学习率影响网络模型的收敛,本文通过依次设置学习率为0.1、0.03、0.01、0.003等的方式进行试验,确定大致区间,最后不断进行调整找到合适的学习率。表1为新英格兰39节点系统仿真算例下不同隐藏层结构的预测误差结果。
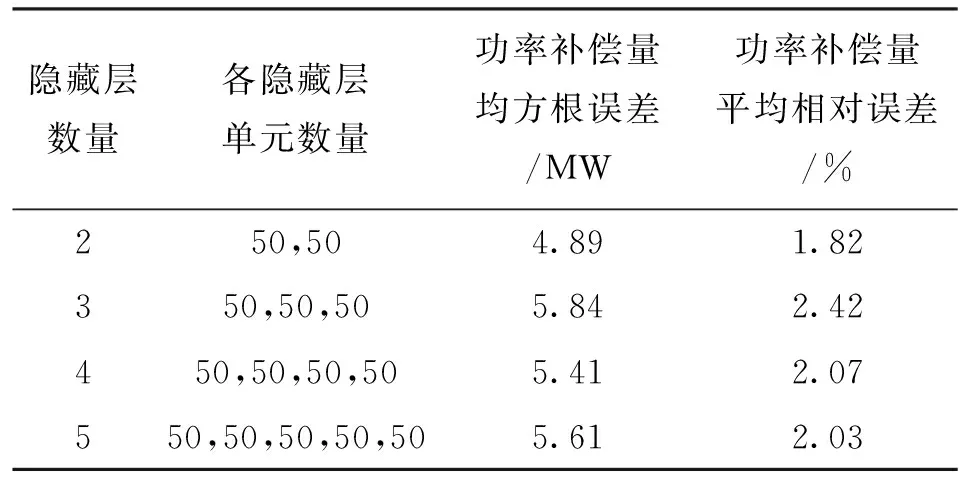
表1 新英格兰39节点系统仿真算例下不同隐藏层结构的预测误差结果
本文最终将DBN模型隐藏层层数设置为4,各层神经元数为26、150、100、100、150、60。无监督学习阶段采用对比散度算法,学习率为0.01,迭代次数为100。有监督学习阶段采用反向传播算法,激活函数采用tanh函数,输出层采用线性函数,学习率为0.04,迭代次数为100。
3.1.3 仿真结果分析 图5和图6分别为选取的某一高频、低频扰动事件的功率补偿量预测曲线对比。
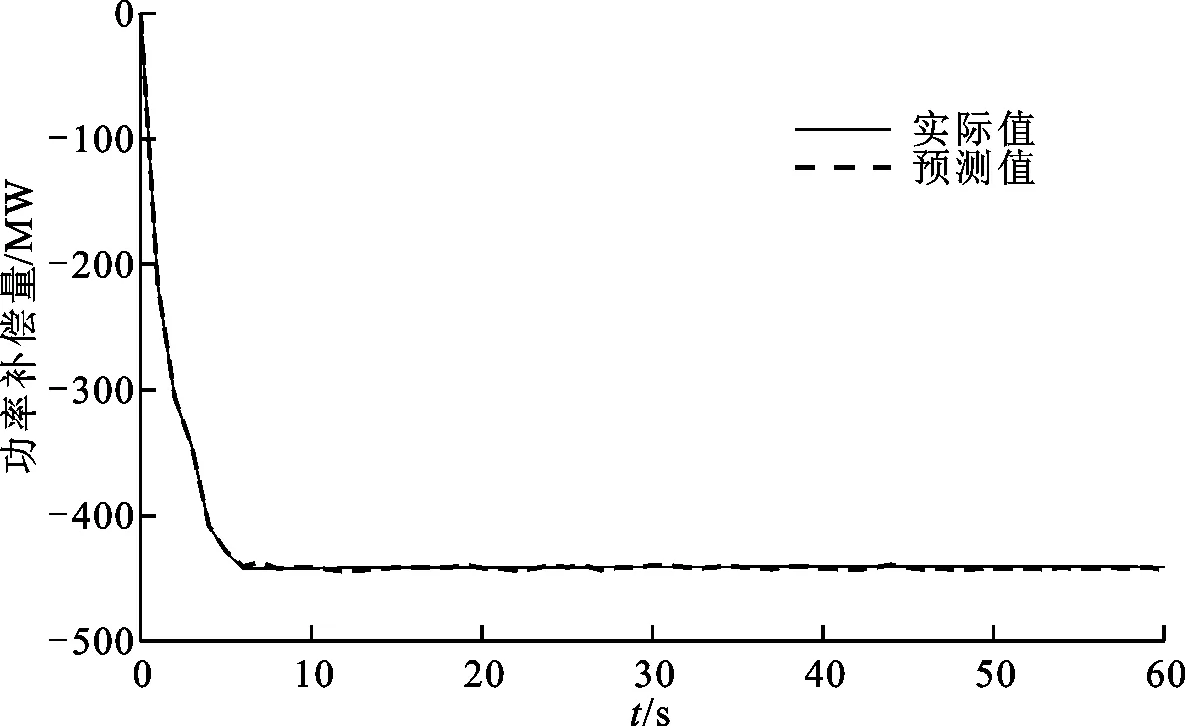
图5 高频扰动事件功率补偿量预测曲线对比
功率补偿量曲线的最大功率补偿量的均方根误差和平均相对误差分别为4.04 MW和1.49%,功率补偿量稳态值的均方根误差和平均相对误差分别为1.42 MW和0.71%,预测结果较准。从图5和图6可以看出:预测曲线可以较精确地预测功率补偿量;高频扰动事件数据由负荷突变生成,数据粒度小,相较于低频扰动事件预测准确率更高。
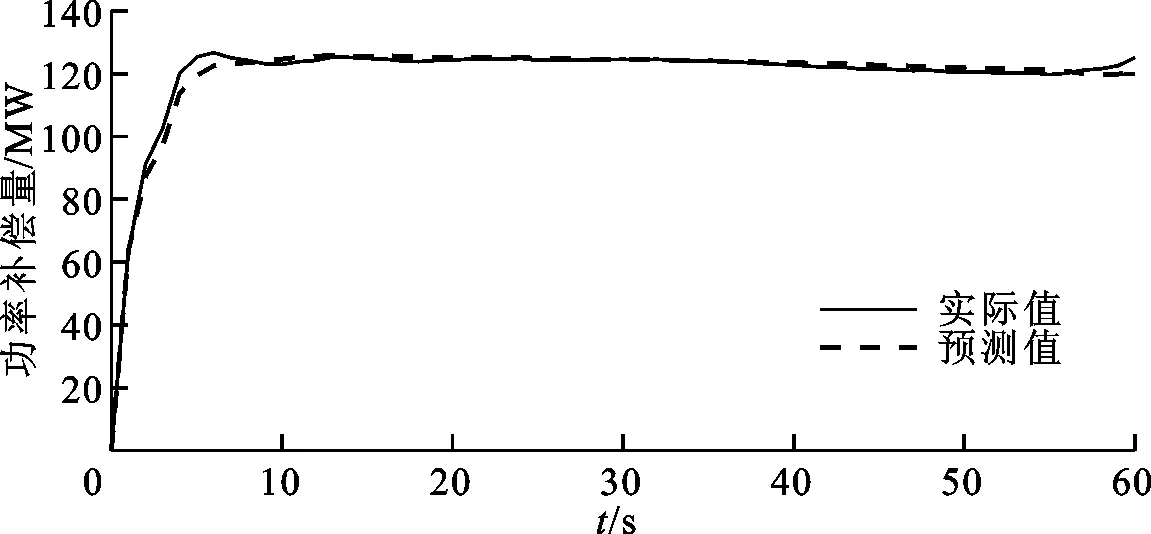
图6 低频扰动事件功率补偿量预测曲线对比
根据本小节仿真结果可知,功率补偿量预测误差很小,均小于1.5%,可以较准确地预测系统功率补偿量曲线,同时单个测试样本的预测时间小于0.05 s,可以满足实际的应用需求。
3.2 电网系统仿真算例
3.2.1 算例系统介绍 选择某电网系统2016—2019年的历史数据,全网参与调频的直调机组有56台(30台火电机组,26台水电机组),其中35台机组装机容量600 MW及以上,17台机组装机容量300 MW及以上,4台装机容量200 MW及以上。电网系统原始数据存在错误数据和无效数据,直接进行训练会导致误差大、速度慢、效果差,因此需要对数据进行处理来获取有效数据集。图7为有效数据集获取过程。
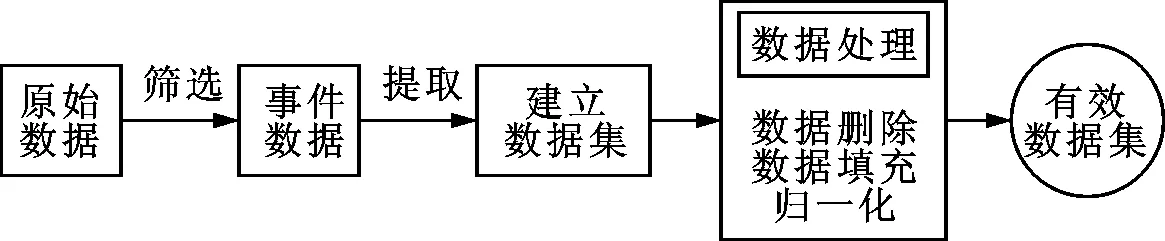
图7 有效数据集获取过程
电网系统历史数据既包含稳定运行的数据,也包含频率事件数据,需要进行筛选。但是,历史数据容易受各种影响,存在许多一次调频回路没有动作的瞬间扰动、数据坏点、高频噪声等。因此,确定一次频率事件为频率偏移超过调频死区,并持续一段时间,具体的选取规则[1]为
(10)
式中:fi为第i时刻的电网频率;fref=50 Hz为电网标准频率;Δf=0.07 Hz为有效扰动频率偏差。
采集的事件数据集存在数据缺失、数据重复、数据无效等问题,直接使用会影响网络模型预测精度。重复数据和无效数据不能为模型的训练提供帮助,甚至会增大误差,因此直接进行删除。对于缺失数据,根据缺失值前后序列的数据均值来进行填充。填补、删除后的数据集中的数据具有较为明显的量级差别,直接进行训练会导致网络模型收敛速度慢且容易产生数值问题。因此,对数据集采用归一化处理,让所有数据保持相同的维度与区间,映射到[0,1]区间上。由于最终获取的数据集本身就存在噪声信号,因而不再对其添加噪声信号分析模型的适应性。
将预处理得到的数据集按照6∶2∶2的比例分为训练集、验证集和测试集共3部分。训练集用于训练网络模型,确定神经网络的参数;验证集用于判断训练结束后的模型性能,调整网络隐藏层数量、隐藏层层数等超参数;测试集用于客观评价网络的性能。经过处理得到2 500组有效数据样本,其中高频事件数据与低频事件数据均为1 250组。按1∶1的比例选取高频与低频事件数据,将1 500组作为训练集,500组作为验证集,500组作为测试集。
3.2.2 模型参数分析 输入层与输出层均只有一层,而隐藏层层数需要根据具体问题进行设置。输入层与输出层的神经元数一般等于输入向量与输出向量的维数。输入特征向量包括机组参数与全网参数共118组参数。机组参数为备用容量和惯性时间常数,参与一次调频的直调机组有56台。全网参数为频率、有功负荷、负荷水平、事件类型、功率缺额和总的备用容量。输出特征向量为系统60 s功率补偿量变化曲线。模型参数选取方法与3.1.2节一致,本文设置输入层和输出层神经元数分别为116和60,各层神经元数为118、100、50、50、50、20、60,隐藏层层数为5。无监督学习阶段采用对比散度算法,学习率为0.06,迭代次数为300。有监督学习阶段采用反向传播算法,激活函数为tanh函数,输出层采用线性函数,学习率为0.03,迭代次数为400。表2为电网系统仿真算例下不同隐藏层结构的预测误差结果。
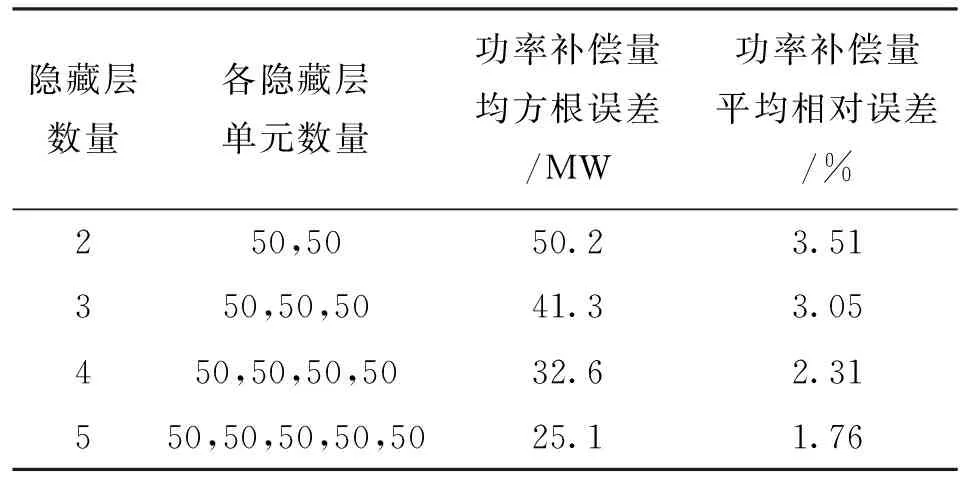
表2 电网系统仿真算例下不同隐藏层结构的预测误差结果
3.2.3 仿真结果分析 为检验模型性能,将DBN模型与DNN模型和RNN模型进行了对比测试。DBN模型层数为6,各层神经元数分别为118、100、50、50、50、20、60。DNN和RNN模型的结构均与DBN设置相同,但不进行无监督预训练,只采用反向传播算法进行监督学习。DNN模型激活函数采用sigmoid函数,RNN模型激活函数采用tanh函数,损失函数均采用均方误差函数,迭代次数为300。表3和表4为3种模型在测试集中的误差结果。

表3 最大功率补偿量误差结果

表4 功率补偿量稳态值误差结果
通过表3和表4可知,DBN模型的预测性能优于其他两种预测模型的。这是因为虽然DNN模型与RNN模型和DBN模型结构参数一致,但DBN模型无监督预训练获得了良好的初值,使得预测准确率提升。RNN模型相较于DNN模型,神经元具有记忆性,可以挖掘数据时序信息,预测精度更高。

图8 高频事件A中3种模型的功率补偿曲线对比
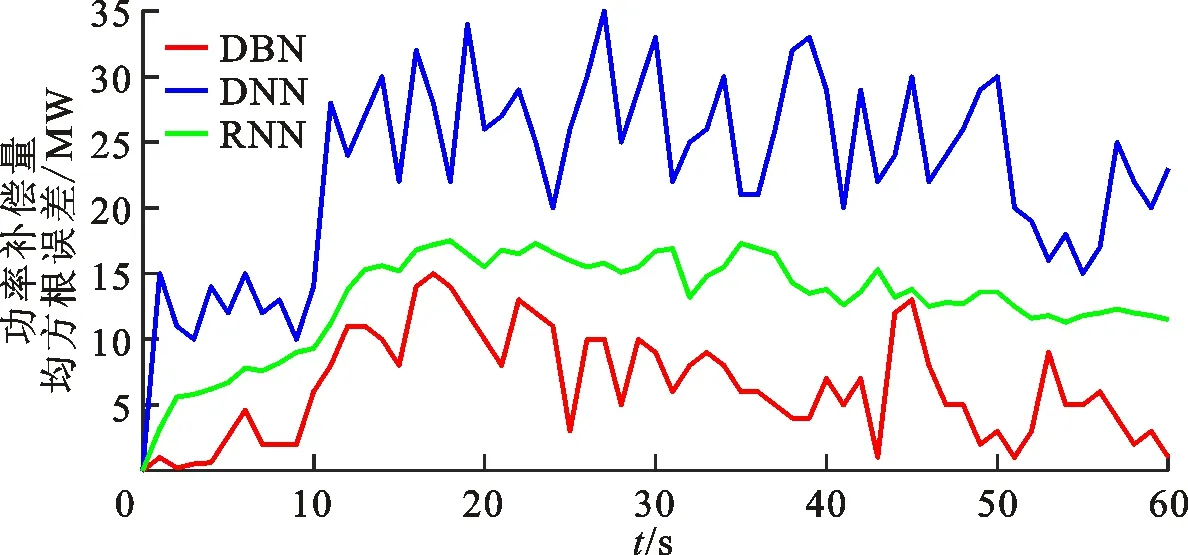
图9 高频事件A中预测模型的功率补偿量均方根误差

图10 高频事件B中3种模型的功率补偿曲线对比
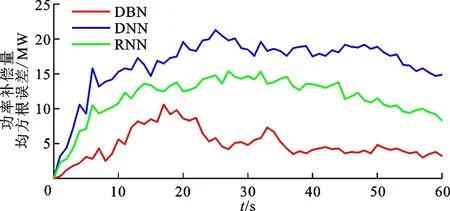
图11 高频事件B中预测模型的功率补偿量均方根误差
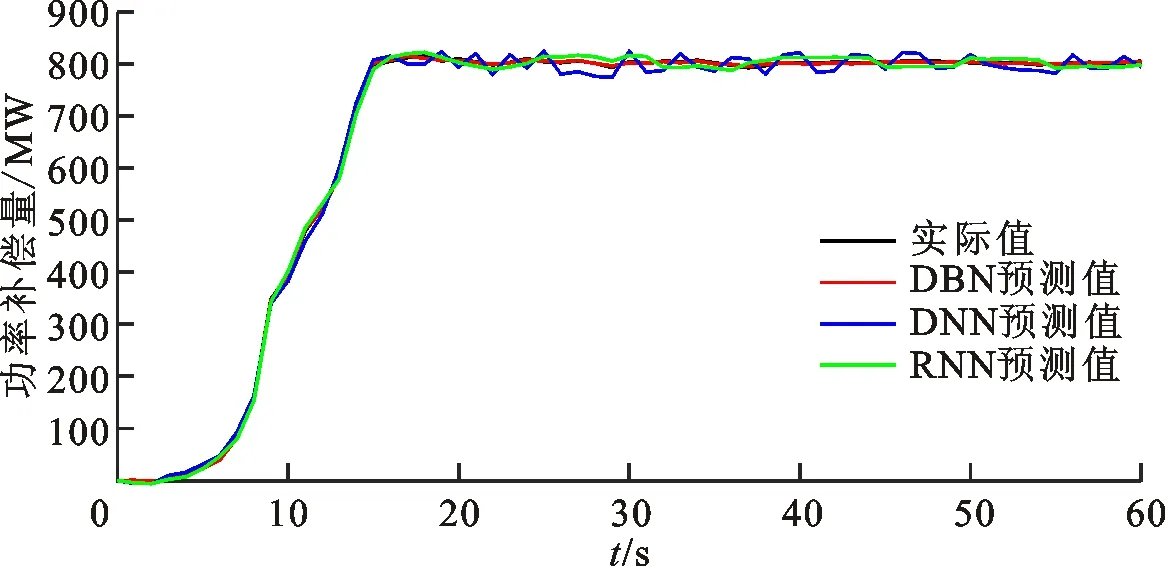
图12 低频事件A中3种模型的功率补偿曲线对比
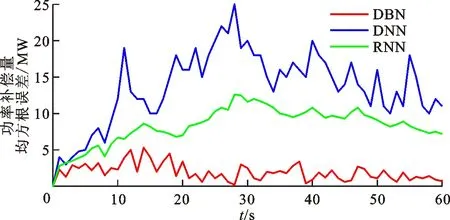
图13 低频事件A中预测模型的功率补偿量均方根误差
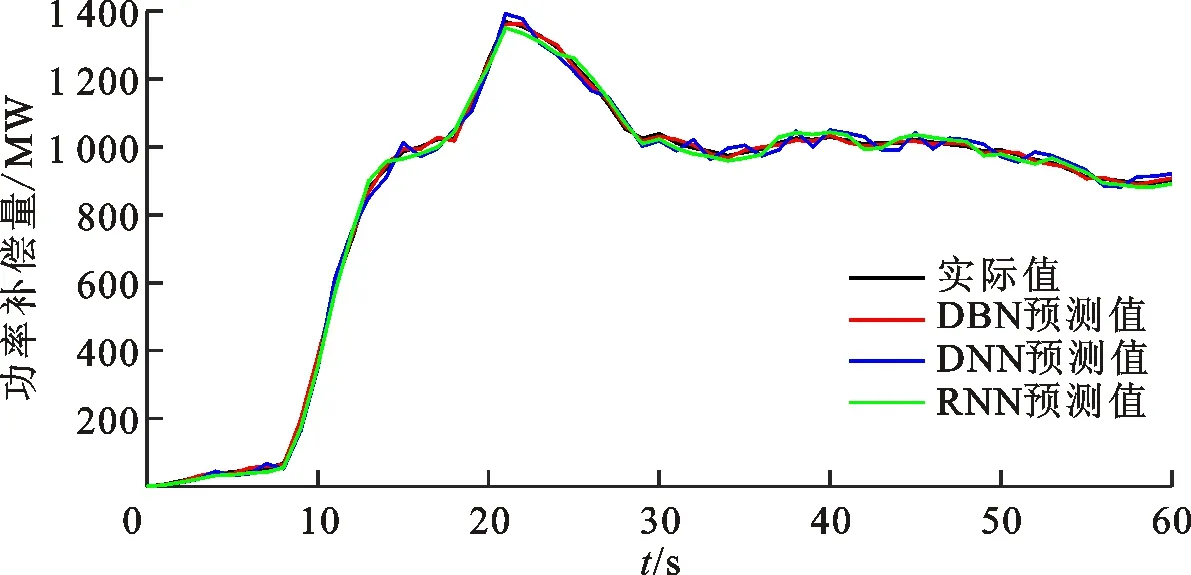
图14 低频事件B中3种模型的功率补偿曲线对比

图15 低频事件B中预测模型的功率补偿量均方根误差
本文分别选取两个高频事件与低频事件,对功率补偿曲线进行分析。图8~11分别为选取的高频事件样本A与B的60 s功率补偿量变化曲线和对应的均方根误差变化曲线。高频样本A为电网某直流极I闭锁事件,事件发生时全网功率缺额约为+1 500 MW;高频样本B为电网某直流极Ⅱ闭锁事件,事件发生时全网功率缺额约为+1 000 MW。图12~15分别为低频事件样本A与B的功率补偿量曲线和对应的均方根误差曲线。低频事件A为某电厂机组故障停机,事件发生时全网功率缺额约为-800 MW;低频事件B为某电厂机组跳闸,事件发生时全网功率缺额约为-1 000 MW。可以看出,无论是高频事件还是低频事件,DBN预测曲线与实际曲线重合度最高、误差最小,DNN预测曲线误差最大。因此,DBN预测曲线的补偿功率稳态值最小、最大有功增量的偏移程度最小,DNN预测曲线的偏移程度最大,符合3.1节的仿真结果。
4 结 论
本文将深度学习应用于电力系统一次调频能力预测,提出一种基于深度置信网络的电力系统一次调频能力预测方法。相较于浅层神经网络的机器学习算法,深度学习可以更好地特征提取,挖掘数据间的隐性联系。本文考虑扰动信息、系统运行状态和机组的状态特征这3种因素,采用机组惯性时间常数、备用容量、系统所有机组的总备用容量、事件类型、功率缺额、系统频率、负荷水平和有功负荷共8维特征作为模型输入,预测扰动后系统的有功功率补偿量动态变化。采用新英格兰39节点系统与某电力系统历史扰动数据进行仿真,与RNN、DNN模型的性能进行对比。结果表明,DBN模型的预测曲线与实际曲线最接近,误差最小,验证了深度信念网络在调频能力预测中的有效性与优越性。DBN模型相较于其他模型,可以通过无监督预训练获得好的初值,挖掘特征间的关系,有效地提升预测的精度。本文通过对功率补偿量曲线的预测,得到扰动后功率补偿量最大值与稳态值,应可为判断扰动危险程度与制定防护控制提供辅助,为人为调控干涉提供依据。
附录A
算法1 对比散度算法(伪代码)
输入:可视层向量v=[v1,…,vm],隐藏层向量h=[h1,…,hn]
输出:连接权重矩阵W=[wij],1≤i≤n,1≤j≤m,可视层偏置向量b=[bj],1≤j≤m,隐藏层偏置向量c=[ci],1≤i≤n
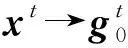
初始化:wij=bj=ci=0,1 (1) fori=1,2,…,ndo (4) end for (5) forj=1,2,…,mdo (8) end for (9) fori=1,2,…,ndo (11) end for (12) fori=1,2,…,n,j=1,2,…,mdo (14) end for (15) forj=1,2,…,mdo (17) end for (18) fori=1,2,…,ndo (20) end for 附录B 算法2 有监督参数微调算法(伪代码) 输出:连接权值矩阵Wk,偏置矩阵bk,其中1≤k≤r,r为网络层数 初始化:使用预训练获得的网络参数Wk、bk (1)fort=1,2,…,Ndo (2) fork=1,2,…,rdo (6) end for (8) fork=1,2,…,r-1 do (10)end for (12)fork=1,2,…,rdo (17)end for (18)end for