近零折射率区超导/介质双层结构的Goos-Hänchen位移
高金霞,武继江
(山东理工大学 物理与光电工程学院,山东 淄博 255049)
超导材料具有一定的不同于传统电介质材料的电磁特性,对含超导材料的各种分层结构光学特性的研究吸引了科研人员的广泛关注[1-3]。Goos-Hänchen(GH)位移是一种特殊的物理光学现象[4]。它泛指光束在一定的界面发生反射时,反射光束相对于几何光学预言的位置在横向上发生了一定位移,这一位移被称为GH位移。一般结构的GH位移在量值非常小,通常为光波长量级,对光学器件的工作过程基本没有影响。近年来随着纳米加工技术的发展,一些光学器件的有效作用尺寸已和光波长相接近,光波在介质界面产生的GH位移,就变成一个非常值得研究的问题。对含超导材料的分层结构,Dadoenkov等人就一维超导光子晶体和含超导材料的三层复合结构的GH位移进行了研究[5-6],得到了一些有意义的结果。
零折射率材料通常是指折射率等于零或近似为零的人工电磁超材料[7]。由于其介电参量具有近零特性,研究人员发现了许多不寻常的光学现象,提出了许多应用。研究表明,超导材料在一定的波段范围内也表现为零折射率材料。在近零折射率区,研究人员对含超导材料的分层结构的光学特性已进行了一定研究,发现了一些奇异的光学特性[8-11]。而对含超导材料的一些光学结构在近零折射率区GH位移的研究近来也开展起来,但所研究的光学结构较为简单[12-13]。对由零折射率材料构成的一定光学结构的GH位移,研究人员也开展了相当多的研究[14-15]。但在这些研究中,近零折射率材料的折射率设定为常数,这不符合近零折射率材料一般为色散材料这一事实。考虑到实际应用,并对上述研究作一定的补充,本文将就由超导材料和传统的电介质材料构成的双层结构的GH位移进行研究。相对于Dadoenkov等[6]所研究的含超导材料的三层复合结构,双层结构在结构上更简单,且在研究中考虑到在Dadoenkov等人的研究中所没有考虑的超导材料的零折射率特性。超导材料的电磁特性可通过外加磁场、温度或压力等物理作用进行调节[3],反之对某一光学结构的光学特性进行测量,可实现对相应物理量的传感测量。基于GH位移效应所实现的传感器件具有较高的传感精确度和探测灵敏度4],因此开展含超导材料的一定光学结构GH位移的研究,对实现低温情况下温度和磁场等物理量的传感测量具有一定的参考价值。随着探测技术的发展,当前完全可以在超低温情况下实现纳米光学尺寸的精密测量[16-17]。
1 计算模型
图1给出了含超导材料双层结构的GH位移示意图。设该双层结构处于自由空间(n0= 1)。根据光波传输所经过的先后顺序,该双层结构如图1所示有超导(S)/介质(D)(定义为SD结构)和介质/超导 (定义为DS结构)两种情况。当光波以入射角θ从自由空间入射到双层结构上,基于稳态相位法,此时所产生的GH位移可表示为
(1)
式中:k0= 2πn0/λ为入射空间中的波矢量;Ф是反射系数r的相位角;λ为真空中光波长。图1中nS(nD)和dS(dD)分别为超导材料(介质材料)层的折射率和厚度。对电介质材料,在计算中选择的是Al2O3材料,其折射率nD= 1.767[6]。对超导材料,选择高温超导材料钇钡铜氧超导体 (YBCO)。对分层结构反射系数r的计算可采用大家熟知的传输矩阵法。

(a) SD结构
根据二流体模型,高温超导体的折射率可以被表示为[9]
(2)
式中:ω为入射光的角频率;μ0和ε0分别为自由空间中的磁导率和介电常数;λL为伦敦穿透深度,其一般可表示为
(3)
式中:T为环境温度;Tc为超导材料的临界温度;λ0为T= 0 K时的穿透深度。由式(2)中可以看出,超导材料的折射率不仅依赖于入射光波的频率,还与温度有关。根据式(2),图2给出了7.7 K和80 K时高温超导材料YBCO的折射率的实部nR和虚部nI随波长的变化曲线。其中虚部nI实际上是大家熟知的消光系数。对超导材料YBCO[9],临界温度Tc= 90 K,T= 0 K时的伦敦深度λ0= 220 nm。
由图2易知,在确定的温度下,在某一波长处nR和nI均为0。定义该波长为阈值波长λth。由图2可以看出,当波长小于λth时,nR为实数,且随着波长的增大,nR逐渐减小。而在大于λth的波段范围内,超导材料表现为零折射率材料。由图2还可看出,温度越高,λth就越大。

图2 超导材料YBCO的折射率随波长的变化曲线Fig.2 Wavelength-dependent refractive index of YBCO at 7.7 K and 80 K
2 数值结果与分析
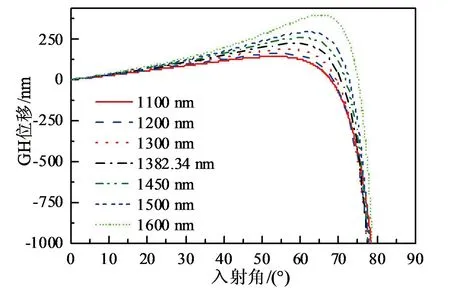
基于上述计算模型,图3和图4分别给出了S波和P波入射时不同波长下的GH位移随入射角的变化曲线。计算中温度取为7.7 K,此时阈值波长λth约为1 382.34 nm。计算中超导层和电介质层的厚度均取为60 nm,其他参数同图2。由图3和图4分可以看出,类似于文献[6]所讨论的三层结构,在掠入射时,GH位移在量值上均随着入射角的增大而急剧增大,所不同的是GH位移的符号存在一定的差异,对S波,GH位移为负值,而对P波,GH位移的正负与结构和入射光波长有关。由于在以较大入射角入射时,GH位移的变化较为简单,后续将主要讨论小角度入射时GH位移的变化规律。
非掠入射时,GH位移随入射角的变化也与结构和入射光波长有关。由图3(a)和(b)可知,在近零折射率区,对S波,各波长下的GH位移随入射角的变化较为一致。随着入射角的增大,对SD结构,由图3(a)可知,GH位移是先增大,达到正的极值后再减小,在减小的过程中由正值变为负值。而对DS结构,由图3(b)可知,各波长下的GH位移保持为负值,且随着入射角的增大而逐渐减小,在量值上则是随着入射角的增大而逐渐增大。由图3(a)和(b)还可看出,此时,GH位移随波长的变化与结构相关。对SD结构,随着波长的增大GH位移逐渐增大,而对DS结构则正好相反。但在量值上二者是一致的,均是随着波长的增大而逐渐增大。
(a)SD结构
对P波,由图4(a)和(b)可知,在近零折射率区,各波长下的GH位移随入射角的变化较为复杂。对SD结构,图4(a)可知,当以阈值波长λth入射时,GH位移基本保持为某一常数而不随入射角变化。当入射光波长小于λth时,GH位移为正值。随着入射角的增大,GH位移基本是先增大后减小而后又增大。当入射光波长大于λth时,GH位移的情况恰好相反。此时,GH位移为负值,且随着入射角的增大,是先减小后增大而后又减小。当小角度入射时,在确定的入射角下,GH位移随波长的变化是一致的,无论入射光波长大于λth还是小于λth,GH位移均是随着波长的增大而逐渐增大,但GH位移在量值上的变化正好相反。

(a) SD结构
类似于SD结构,对DS结构,当P波入射时,GH位移随入射角的变化也以λth为分界波长。但此时以λth入射时,GH位移不再保持为某一常数,而是随着入射角的增大而逐渐增大。当入射光波长大于λth时,GH位移随入射角的增大是先增大后减小而后又增大。当入射光波长小于λth时,若入射光波长濒临λth,GH位移随入射角的增大是先减小后增大,达到极值后又先减小后增大。若入射光波长远离λth,GH位移则随入射角的增大是先减小后增大。小角度入射时,无论入射光波长大于λth还是小于λth,GH位移均是随着波长的增大而逐渐减小,但在GH位移在量值上的变化正好相反。
综合图4(c)和(d)的结果可知,对P波,小角度入射时,无论是SD结构还是DS结构,入射光波长越接近λth,对应波长的GH位移在量值上就越大。此外,在小角度入射时,濒临λth的各入射光波长下GH位移随入射角变化时有一个或两个极值。如对DS结构,以波长1 370 nm入射时,在入射角约为5°和18°附近,GH位移曲线有两个极值。需要说明的是,当入射光波长远离λth时,GH位移的变化规律将与上述结果会有所不同。
上述计算中,超导层和电介质层的厚度dS和dD固定为60 nm,而它们的取值对GH位移有很大影响。由上述计算结果可知,相对而言,P波入射时DS结构的GH位移随入射角的变化较为复杂,因此后续将主要研究P波小角度入射时,DS结构的GH位移随dS和dD的变化情况。
(a) 入射光波长1 370 nm
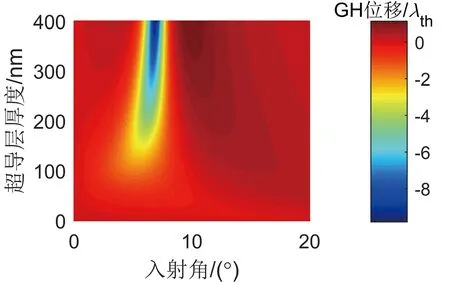
对DS结构,图5给出了P偏振光入射时,入射光波长分别为1 370 nm (小于λth)和1 390 nm (大于λth)的光波的GH位移在小角度入射时随超导层厚度dS变化情况。图中GH位移量值的表示以λth为单位,下同。计算中,电介质层的厚度dD保持为60 nm不变,其他参数同图3。由图5可知,dS对两个波长下GH位移的影响存在一定的差异。由于小角度入射时第二个极值的GH位移相对于第一个极值要小很多,后续将主要讨论第一个极值的变化情况。由图5(b)可知,当入射光波长为1 370 nm时,随着的dS增大,第一个极值向大角度方向移动,且dS越大,GH位移在量值上就越大,在dS为400 nm时GH位移的大小约为10λth。由图5(b)可知,当入射光波长为1 390 nm时,两个极值随dS的变化基本一致,均随着dS的增大向小角度方向移动,GH位移的极值均是先增大后减小,因此存在相应的最佳dS分别使得两极值达到最大。

(a) 入射光波长1 370 nm
类似于图5、图6给出了小角度入射时两不同入射波长下的GH位移随电介质层厚度dD的变化情况。由图6(a)可以看出,在所计算的dD的变化范围内,波长1 370 nm的GH位移的第一个极值随着dD的增加向小角度方向偏移,且随着dD的增大而逐渐减小。可以看出,在近零折射率区,要得到较大的GH位移,dD的取值应为零,也即不加载电介质层。计算表明,当dD取值为零时GH位移可达280λth。为清晰显示GH的变化趋势,图6(a)中GH位移取值较大的区域和色柱的范围做了一定的处理。进一步的计算表明,当入射光波长远离λth时,要得到较大的GH位移,dD不能为零。入射光波长为1 390 nm时,GH位移随的变化与上述情况不同。由图6(b)可以看出,随着dD的增大,第一极值首先向大角度方向移动而后偏向小角度方向。第一极值随着dD的增大是先增大后减小,存在一个最佳的dD使得GH位移最大。
在小角度入射时,对比图5和图6所给出的GH位移曲线第一个极值随dS和dD变化情况可以看出,当入射光波长小于λth时,要使第一个极值的量值尽可能大,需要dS尽可能大,而dD要尽可能小。而当入射光波长大于λth时,dS和dD则存在最佳的取值使得GH位移在某一入射角下达到最大。

图7 温度对GH位移的影响Fig.7 The effect of temperature on the GH shift
超导材料的折射率是温度的函数,对图1所示结构也可进一步讨论温度对GH位移的影响。图7给出了波长为1 380 nm的P波在小角度入射时,DS结构的GH位移随温度的变化情况。计算中,dS和dD的取值分别为100 nm和35 nm。由图可以看出,随着温度的增加,GH位移的极值均逐渐减小,且向大角度方向移动。由图2可知,温度变,λth也随之变化,近零折射率区也随之变化,因此图7的计算结果已超出本文计划讨论的范围。但由图7可知在合理选择相关参数的情况下,图1所示的含超导材料的双层结构可以有较大的可以实现实际检测的GH位移,如图7所示计算结果中最大可达12λth,这对实际中基于GH位移实现超低温情况下温度的传感测量具有一定的参考作用。
3 结论
在近零折射率区,理论研究了由超导材料和电介质材料构成的双层结构的GH位移。结果表明,当入射光掠入射时,该双层结构GH位移随着入射角的增大而急剧增大,而非掠入射时,GH位移与入射光的偏振状态密切相关。S波入射时,GH位移随相关参数的变化较为简单。对SD结构,GH位移随着入射角的增大是先增大后减小。对DS结构,GH位移随着入射角的增大而逐渐减小。P波入射时,GH位移以阈值波长λth为分界波长表现出不同的变化规律。但无论是DS结构还是SD结构,当小角度入射时,入射光波长越接近λth,GH位移的极值在量值上就越大。研究还表明,小角度入射时,对DS结构,P波的GH位移随两介质层厚度dS和dD的变化与入射光波长相关。当入射光波长小于λth时,要使GH位移尽可能大,dS要尽可能大,而dD要尽可能小。当入射光波长大于λth时,dS和dD则存在最佳的取值使得GH位移达到最大。超导材料在光子学领域具有广泛的应用,计算结果为基于超导材料的新型光子学器件研究开发提供了参考。

