基于隐马尔可夫模型的半挂车制动侧滑状态辨识

步玫，宇仁德，吕安涛,2，马晨浩，胡婧晖

(1.山东理工大学 交通与车辆工程学院,山东 淄博 255049；2.山东省交通科学研究院,山东 济南 250100)

目前，从我国的货物中转量来看，半挂车凭借它的较大货运量完成了57.23%的货物中转，成为了公路运输的主力[1]。同时，半挂车侧滑事故也在日益增多，半挂车发生制动侧滑后横向先前移动，因其车身较长和自身质量大的特点，横向滑行产生惯性造成的冲击力较大，因此一旦发生事故往往较为严重。综上所述，研究半挂车制动侧滑的稳定性对道路交通安全具有重要意义。

在车辆状态辨识方面，很多学者都进行了卓有成效的研究。史培龙等[2]首先采用PCA降维的方法对气压制动系统状态进行辨识，然后运用驾驶人制动意图与制动系统响应的双层隐马尔可夫模型对系统状态进行识别，并分别依据实车试验数据对模型进行离线训练和在线辨识验证；孟妮等[3]建立了基于RBF神经网络的驾驶人无意识车道偏离识别模型,并通过归一化、主成分分析和遗传算法对神经网络的权值和阈值参数进行优化,提高了神经网络模型总体识别率；徐强[4]将CarSim仿真数据通过K均值聚类的方法对车辆行驶状态数据进行离线聚类,得到4个离线聚类质心，搭建了CarSim与Simulink联合仿真平台，基于车辆实时行驶数据与离线聚类质心之间的欧氏距离设计了车辆横向稳定性判定准则，对车辆行驶状态进行实时划分与识别；唐智慧等[5]应用Kohonen神经网络对表征驾驶行为状态的9个指标组成的向量进行非监督聚类，用聚类结果组成的时间序列表示驾驶员行为指标的动态变化特征并以此作为输入，通过训练SVM实现驾驶行为险态辨识，解决了高维指标数据监督聚类困难和险态识别的静态性问题，并采用驾驶模拟器进行试验设计，对方法的有效性进行验证；游忍等[6]针对现有汽车防撞高速扇形模型提出了基于双重扩展卡尔曼滤波的高速扇形预警模型，根据车辆状态和路面附着系数估计实现了制动闭环控制；崔宇等[7]采用小波神经网络对车辆运行状态进行识别，对样本进行主成分分析、卡尔曼滤波，利用遗传算法优化小波神经网络，优化后的小波神经网络对数据进行训练与测试，解决了车辆安全辅助系统中对车辆运行状态识别率偏低的问题；刘通等[8]重点从车辆典型危险行驶状态的识别、检测2个方面，梳理纵向及横向危险行驶状态及其表征参数，总结主要的识别与检测方法，得出了隐马尔可夫模型对危险驾驶事件的识别准确率相对较高的结论。尽管上述方法在车辆状态辨识上都有显著效果，但由于车辆状态的影响因素过多，从而也导致了模型中数据维度过高、训练时间过长且辨识率偏低等缺点的存在。

本文选取重心横向位置、重心纵向位置、制动初速度和路面摩擦系数4个重要影响因素作为模型的特征参数，在ADAMS中建立整车模型和道路模型进行直线制动仿真实验，得到一系列特征参数仿真数据以及每条数据的仿真状态，并选用Baum-Welch算法多次迭代得到HMM最优参数，以提高HMM模型的辨识准确率。

1 半挂车模型直线制动仿真实验

1.1 基于ADAMS/CAR半挂车模型的构建

依据ADAMS/CAR中整车虚拟样机的建模原则，本文所建的半挂车模型包括牵引车和半挂车两大部分。牵引车为前桥转向后双桥驱动，转向桥采用钢板弹簧作为弹性元件，驱动桥采用空气弹簧为弹性元件，由刚体车轴、减振器及横、纵向拉杆等组成;半挂车由双支撑、车身、轮胎等组成，采用空气弹簧作为弹性元件[9]。将上述各子系统通过相应的通讯接口组装成的半挂车仿真模型如图1所示。

图1 半挂车模型Fig.1 Semi-trailer model

1.2 道路模型的构建

在ADAMS/CAR标准模式下通过Road Builder建立一条直线形道路，保持其他参数不变，主要修改路面的摩擦系数即可，建好的3D道路仿真模型如图2所示。

图2 道路模型Fig.2 Road model

1.3 整车制动仿真

ADAMS/CAR通过在hps_frame_cg中改变质心坐标来调整重心位置，模拟车辆的重心偏移。实验所构建半挂车模型的质心原点，也即重心初始位置(x,y,z)=(10 025 mm，100 mm，1 128 mm)，且定义X轴，Y轴和Z轴方向的移动分别代表重心的纵向、横向偏移和高度变化。在进行直线制动仿真实验后，通过ADAMS/PostProcessor输出的车速曲线图，分别观察重心在3个方向偏移时半挂车速度的变化情况可知，横、纵向偏移对安全行车速度影响明显，且分别在横向偏移1dm和纵向偏移5 dm时更易观察变化趋势；因此，重心横坐标在初始位置基础上取值为100 mm、200 mm、300 mm、400 mm，同样纵坐标取值为10 025 mm、10 525 mm、11 025 mm、11 525 mm。重心高度的变化对车速的影响不明显，这跟半挂车自身重量较大有关，在这里只考虑重心的横、纵向偏移。

修改道路属性文件中的路面摩擦系数，分别取值0.8、0.7、0.6、0.5。最后在如图3所示的对话框中输入相应数据进行制动仿真实验，设置制动减速度为0.4g，初始速度分别从低、中、高车速中随机取值，其他参数保持不变。

图3 直线制动仿真参数输入界面Fig.3 Straight brake simulation parameter input interface

仿真结束后，通过ADAMS/PostProcessor模块分别输出车身侧滑角曲线图和左右外侧后轮所受侧向力对比曲线图，综合两个曲线图判断此次仿真是否已经发生侧滑。当重心横向位置为100 mm、纵向位置为11 025 mm、路面摩擦系数为0.8、制动初速度为84 km/h时输出的两种曲线图如图4和图5所示。可以看出，半挂车在第4 s的时候车身侧滑角远远大于0°，且左右两轮所受侧向力方向一致，说明在此速度下车辆已经发生了侧滑。通过ADAMS输出多组仿真数据以及每条数据的制动侧滑状态，根据仿真状态将这些数据划分为安全与危险两组。

图4 半挂车的车身侧滑角Fig.4 Side slip angle of semi-trailer

图5 左右后轮受力对比图Fig.5 Force diagram of left and right rear wheels

2 基于HMM的半挂车制动侧滑状态辨识模型的建立

本文主要研究利用重心横向位置、重心纵向位置、路面摩擦系数、制动初速度这4个特征参数组，表征制动未发生侧滑的安全状态和已发生制动侧滑的危险状态。隐马尔可夫模型可以定义为五元组λ={N，M，π，A，B}，下面对各参数的意义进行说明。

车辆制动侧滑状态不能直接被观察到，也就是HMM中所说的隐状态，用参数N表示隐状态数。本文的制动侧滑状态包括表征安全的状态辨识1和表征危险的状态辨识2，所以N=2。

制动侧滑的安全与危险两种状态虽然不能直接通过观察获得，但是本文所选取的重心横向位置、重心纵向位置、路面摩擦系数、制动初速度4个观测信息均可以直接获得；同时，这些观测信息可以表征制动侧滑的两种隐状态，也就是HMM中所说的观察状态，用参数M表示可观察状态的数目，所以M=4。

λ=(π，A，B)称为隐马尔可夫模型的三要素，π和A决定状态序列，B决定观测序列。状态转移概率矩阵A表示安全与危险两个隐状态之间相互转移形成的概率矩阵；观测概率矩阵B表示重心横向位置、重心纵向位置、路面摩擦系数、制动初速度4个特征参数值之间相互转移形成的概率矩阵；初始状态概率向量π为制动侧滑的两个隐状态所形成的初始概率矩阵。

3 HMM制动侧滑状态辨识算法及原理

3.1 Baum-Welch算法

Baum-Welch算法首先对HMM的参数进行初始估计，然后通过给定的数据评估这些参数的价值、减少它们所引起的错误并重新修订这些参数；因此，对于给定的一组观察序列，利用算法来估计一个最合适的HMM，也就是确定对已知序列描述最合适的λ=(π,A,B)三元组。

该算法本质上使用的就是EM(最大期望算法)的原理，即通过一种极大似然对数值(该值反映训练出的模型与实际模型的接近程度，值越大越接近，也称似然度[10])方法，不断迭代训练参数直到HMM模型收敛，最后得到最优参数。具体的参数学习过程如下：

1)参数初始化。随机给πi，aij,bjk赋值，得到模型λ0，设i=0。

初始概率矩阵表达式为

(1)

转移概率矩阵表达式为

(2)

观测概率矩阵表达式为

(3)

式中:O和q分别为观测序列和状态序列。

4)保存模型参数。

3.2 辨识原理

本文采用的是一种离散的隐马尔可夫模型(DHMM)，首先分别对两种隐状态和4个特征参数进行分类编码，见表1和表2(其中表2中车速的编码原则是使每个区间内同时包含制动安全、危险两种状态)；然后将所有的特征参数组作为观测序列输入到模型中进行机器学习和参数优化；最后利用建立好的HMM模型对十组具有代表性的特征参数值进行状态辨识，其辨识原理如图6所示。两种辨识状态分别对应两个HMM辨识器，并且会产生两个似然对数值Logi(P(O|λi))(i=1,2)，即每种状态都会有一个专属的HMM，当输入一组某状态的特征参数数据时，此状态对应的似然对数值就会最大。

表1 制动侧滑状态的分类编码Tab.1 Classification and coding of braking sideslip

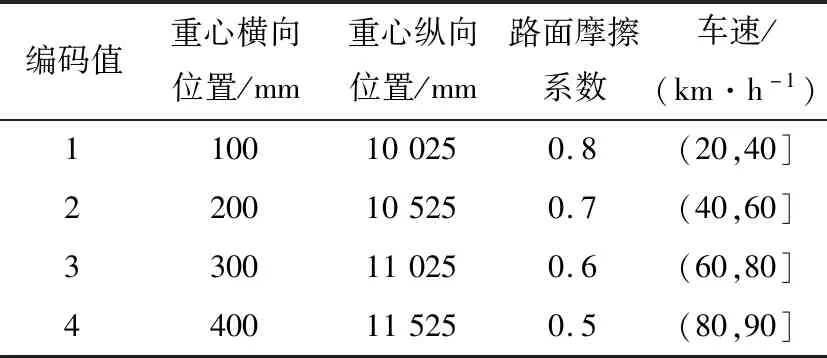
表2 特征参数的分类编码Tab.2 Classification and coding of feature parameters

图6 HMM的辨识原理图Fig.6 HMM state recognition process diagram

4 HMM制动侧滑状态辨识模型验证

4.1 参数输出

通过MATLAB软件对Baum-Welch算法进行编程，将包含安全与危险两种状态的仿真数据输入到隐马尔可夫辨识模型中进行参数迭代训练，并通过似然度曲线变化图可得迭代20次后安全状态HMM1和危险状态HMM2均达到收敛，如图7所示。此时输出优化后的两模型参数πi，Ai，Bi(i=1,2)，如下：

λ1=(π1,A1,B1)，

λ2=(π2,A2,B2)，

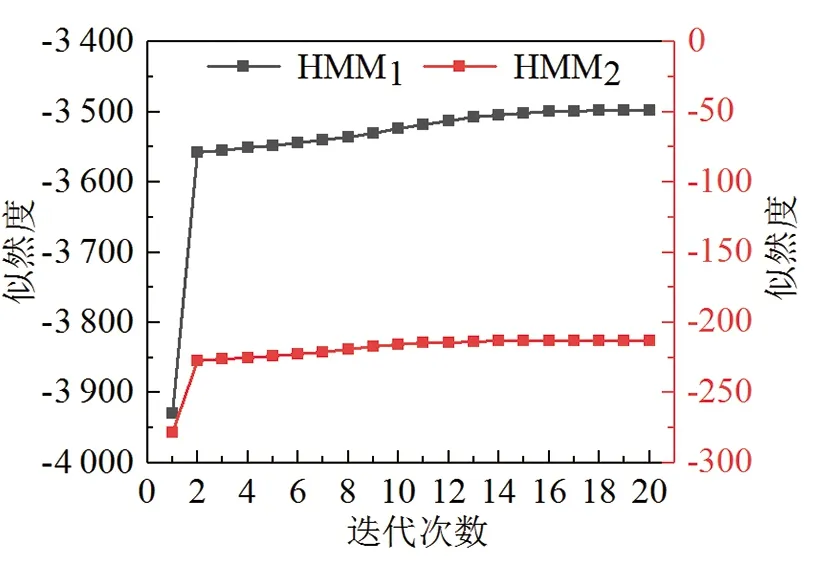
图7 HMM的似然度曲线变化图Fig.7 HMM learning curve with iterations

4.2 辨识结果

半挂车制动侧滑状态辨识结果见表3。分别选取5组安全和危险状态下的特征参数样本，并给出与这10组样本数据相对应的制动侧滑状态HMM输出的Logi(P(O|λi))。表3中显示的这个似然对数值(负值)越大，说明某特征参数样本与HMMi匹配程度越高，也即为该模型所对应的辨识状态，表中用深色标注出正确的辨识结果，证明此辨识模型的有效性。

表3 半挂车制动侧滑状态辨识结果Tab.3 Identification results of brake slippage of a semi-trailer

4.3 准确性验证

为了进一步验证HMM制动侧滑状态辨识模型的准确性，将其与RBF神经网络辨识算法[3]和BP神经网络辨识算法[11]进行对比，随机选取100组测试样本分成10次进行辨识，记录每一次得到的3种模型的准确率，对比结果如图8所示。由图8可知，本文所提出的HMM辨识模型优于其他两种模型，且辨识准确率接近90%。

图8 三种模型辨识准确率对比图Fig.8 Comparison chart of three models′ recognition accuracy

5 结束语

车辆状态辨识是主动监控预警技术的核心要素之一，本文通过ADAMS制动仿真实验得到重心横向位置、重心纵向位置、路面摩擦系数、制动初速度4个特征参数，构建了一种基于隐马尔可夫模型的制动侧滑状态辨识模型，通过Baum-Welch算法实现了HMM模型的优化。辨识结果表明，优化后的模型能够有效辨识半挂车的制动侧滑状态；准确性验证表明，此模型具有辨识率高和鲁棒性好等优点。