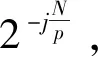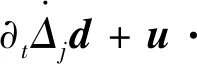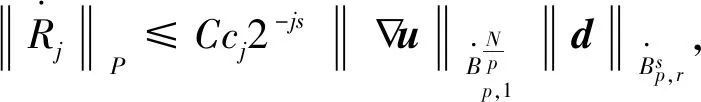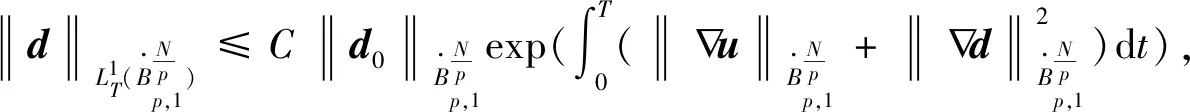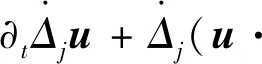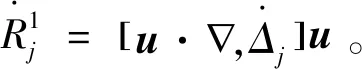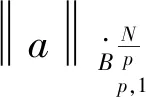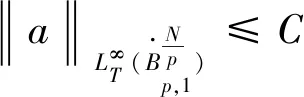密度依赖的不可压缩液晶模型的爆破准则
张明雪,王昌花
(1.山东理工大学 数学与统计学院,山东 淄博255049;2.张店区第九中学,山东 淄博255040)
1 模型和主要结果
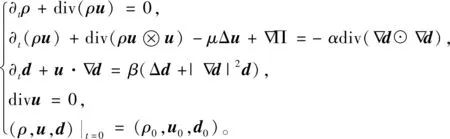
(1)
式中:ρ∈是流体的密度函数;u∈N是速度场;d∈SN-1(N中的单位球面)是代表宏观分子取向的单位矢量场;标量函数∏∈是压力;正常数μ,α,β分别代表粘度,动能与势能之间的竞争,微观弹性弛豫时间或分子取向场的Deborah数,因为α,β的确切值在分析中不起作用,所以可以取α=β=1;符号⊗表示Kronecker张量积,因此u⊗u=(uiuj)1≤i,j≤N;d⊙d表示第i、j个元素为∂xid·∂xjd(1≤i,j≤N)的矩阵。实际上,d⊙d=(d)Td,其中(d)T表示N×N阶矩阵d的转置。
对于所有l>0,注意到系统(1)在以下变换中保持scaling不变:
(2)
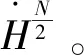

(3)
Xu等[5]在密度场具有小性条件下证明了系统 (1) 的局部适定性和小初值意义下的整体适定性。
命题1 设1
此外,如果存在一个正常数η1使得
则可以取T=+。另外,如果1 徐夫义等[6]对多维可压缩液晶流体进行了类似研究。需要指出的是,该模型大初值意义下的整体适定性仍是一个公开问题。本文探索的是方程中影响局部解延拓到整体解的因素,即该模型的爆破准则问题。 满足 (4) 则(a,u,d)在t=T*之后可以延拓。 容易得到 成立,则称作f的Littlewood-Paley 分解。 定义1[7]令s∈,1≤p,r≤+,定义齐次Besov空间为 其中 在Besov空间中,有以下常用的乘积估计。 命题2 对于所有的1≤r,p,p1,p2≤+,存在一个正常数使得 命题3 令1≤p1≤p2≤+,假设f∈Lp1(N),则对于任意γ∈(∪{0})N,存在不依赖于f,q的常数C1,C2,使得 命题4 令1≤p,p1≤,1≤r≤和σ∈,则存在一个只依赖于σ的常数C>0,使得对任意的q∈,有 其中交换子[·,·]定义为[f,g]=fg-gf,并且(cj)j∈表示一个序列满足 根据临界Besov空间中MHD系统的正则性准则的证明过程[8],证明定理1,为此,本文只需要证明存在常数C>0,使得下面的式子成立 (5) (6) (7) 对于式(7)左边的第二项,由Bernstein 不等式可以得到 (8) 所以,式(7)变为 (9) 由交换子估计: (10) 有 所以, 由Gronwall不等式,可得 (11) 此外,还可得到 (12) 由式(11)、(12)有 (13) ∂tu+u·u-μΔu=F, (14) 式中F≜μaΔu-(1+a)div(d⊙d)-(1+a)∏。 (15) (16) 类似于式(8),有 即 由交换子估计式(10),有 所以, (17) 下面估计F。由乘积估计,有 (18) 对于F第二项(1+a)div(d⊙d),由乘积估计,插值不等式及式(13)有 (19) 估计F第三项(1+a)∏。首先将散度算子div作用于式(3)中的第二个方程,得到 -Δ∏=div(a∏)-divG, 其中G=μaΔ∏-u·u-(1+a)div(d⊙d)。由乘积估计及Bernstein不等式,有 (20) 结合式(18)、(19)和(20)可得 (21) 由Gronwall 不等式有 定理1得到证明。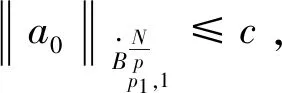
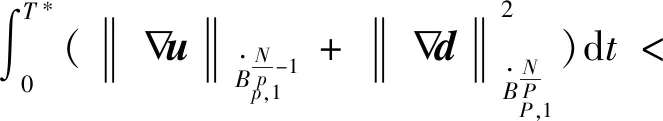
2 预备知识
2.1 Littlewood-Paley 分解
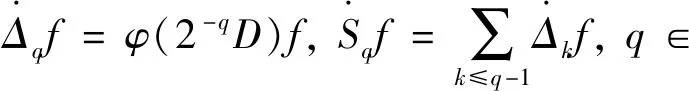

2.2 齐次Besov空间

2.3 伯恩斯坦不等式
3 定理1证明