基于扩张状态观测器的双桨推进无人艇抗干扰目标跟踪控制

吴文涛，彭周华，王丹，刘陆，姜继洲，任帅

大连海事大学 船舶电气工程学院，辽宁 大连 116026

0 引 言

近年来，随着无人驾驶技术的兴起和发展，无人艇(unmanned surface vehicle, USV)作为一种小型化、智能化、多用途无人海洋运载平台，获得了学者们的广泛关注。从运动场景来看，无人艇可用于轨迹跟踪、路径跟踪和目标跟踪，而目标跟踪技术在军事和民用领域具有重要的应用价值[1]。

无人艇的运动控制面临着非线性、模型不确定性、欠驱动和强外部扰动等研究难点，给无人艇有效可靠的目标跟踪控制带来了挑战。目前，研究人员已提出众多方法用于无人艇控制，如滑模控制[2]、鲁棒控制[3]、模糊控制[4]、参数自适应控制[5]、神经网络控制[6]、扰动观测器[7]、扩张状态观测器[8]等。传统的无人艇运动是通过调节螺旋桨和舵机来实现姿态控制，该方法较适用于大型船舶。因舵机需要频繁调整舵角来控制船舶的航向姿态，故难以满足对灵敏性要求较高的小型无人艇。相较之下，双桨推进无人艇由于是通过2 个螺旋桨推力相同或不同来进行速度或航向的控制，能在很大程度上提高无人艇的灵敏性和机动能力，可使无人艇更好地适应工作场景的需要[9]。

本文将研究含模型不确定性与未知海洋环境扰动的双桨推进欠驱动无人艇抗干扰目标跟踪控制问题。首先，建立双桨推进欠驱动无人艇的运动数学模型，包括运动学方程和动力学方程。在运动学层级，提出基于平行接近制导(constant bearing, CB)的目标跟踪制导律；在动力学层级，设计基于扩张状态观测器(extended state observer,ESO)的纵荡速度控制律和艏摇角速度控制律，以消除模型不确定性与未知海洋环境扰动问题，实现无人艇的抗干扰目标跟踪控制。最后，通过输入状态稳定性定理和级联定理，分析所提出的基于ESO 的纵荡速度和艏摇角速度控制器的稳定性，并用实验证明采用CB 制导的抗干扰目标跟踪控制方法的有效性。

1 无人艇数学模型

在地球坐标系XE-YE和艇体坐标系XB-YB下，双桨推进的欠驱动无人艇运动的数学模型[10]如图1 所示。

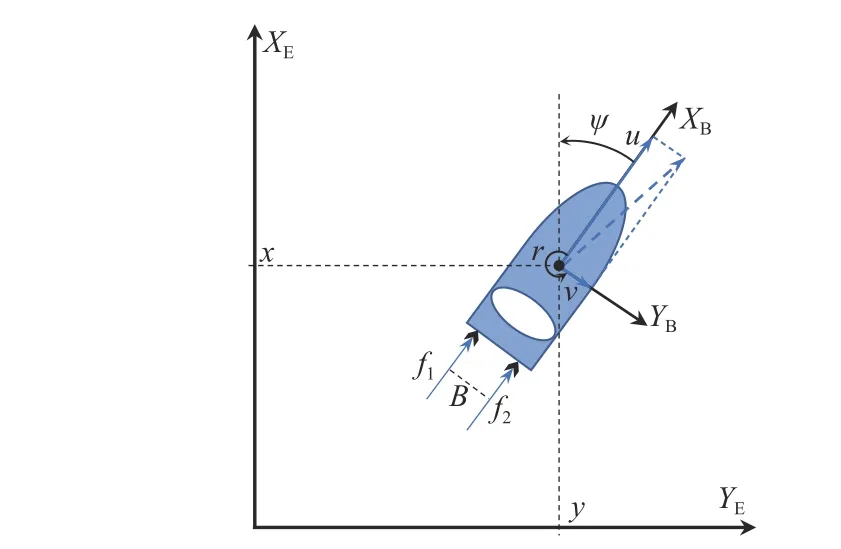
图1 无人艇平面运动示意图Fig. 1 Schematic diagram of plane motion of USV

图中：u,v,r分别为无人艇在艇体坐标系XBYB下的纵荡速度、横荡速度和艏摇角速度；x,y,ψ分别为无人艇在地球坐标系下的XE坐标、YE坐标和偏航角；f1和f2分别为左、右螺旋桨产生的推力；B为左、右螺旋桨之间的横向轴距。

无人艇的运动学模型可由一个三自由度非线性数学模型描述[11]：

式中： υ=[u,v,r]T，为无人艇的速度状态向量；η=[x,y,ψ]T， 为无人艇的位置状态向量；R(ψ)为无人艇在地球坐标系和艇体坐标系下的矩阵。

在动力学建模中，无人艇在水面航行时的水动力阻尼项通常采用线性形式，即无人艇所受阻力与速度成线性关系。因此，无人艇的动力学方程可由如下方程描述[11]：式中：M为无人艇的惯性质量矩阵；C为向心力和科氏力系数矩阵；D为水动力阻尼矩阵； τ为无人艇的推力及其力矩向量； τd为推力和力矩扰动项向量。

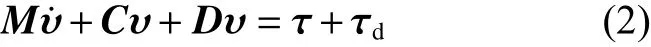
式中：d11,d33为 阻尼系数且d11,d33∈D；m11,m33为惯性质量常数且m11,m33∈M；k为直流电机输入电压与产生的推力关系参数； τd1∈τ，为纵荡速度方向扰动分量， τd3∈τ，为艏摇角速度方向扰动分量。由式(3)可知，仅通过调节控制电压 σu或 σr就可控制无人艇的动作状态，实现其纵荡速度和艏摇角速度的解耦控制，简化了双桨推进无人艇动力学控制器设计，也解决了运动控制过程中回转运动和推进运动耦合的问题。

2 控制器设计

2.1 运动学制导律设计

CB 制导的基本原理是通过将视距旋转率降低到0，从而使跟踪艇以恒定的方位感知并跟踪目标。目标跟踪是将跟踪艇与目标的视距降低到一个期望值并保持。

定义某时刻跟踪艇和目标的位置矢量分别为p(t)=[x(t),y(t)]T和pt(t)=[xt(t),yt(t)]T，则跟踪艇和目标的速度矢量分别为ϑ (t)=dp(t)/dt≜p˙(t) 和ϑt(t)=p˙t(t)。 令p˜(t)=pt(t)−p(t)，为目标和跟踪艇的视距矢量，则CB 制导的控制目标可以表述为

CB 制导律的速度分解关系如图2 所示。

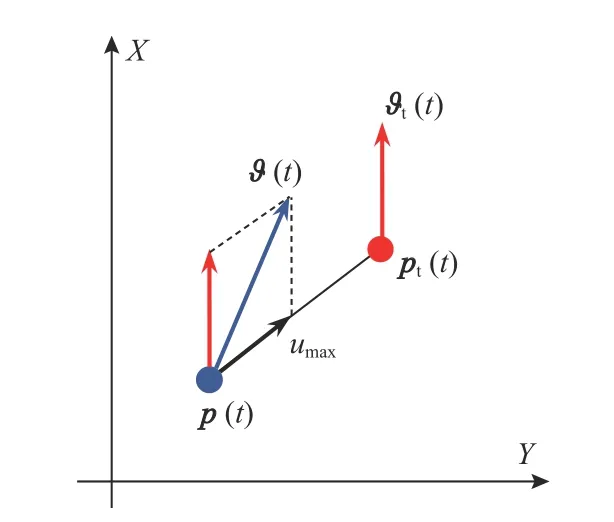
图2 CB 制导律速度分解图Fig. 2 The velocity assignment associated with CB guidance

根据图2，得[13]

式中：umax为跟踪者沿视距方向的最大靠近速度，umax＞0 ； δp˜为 防 碰 撞 常 数， δp˜＞0。因 此，基于CB原理的运动学制导律如下：

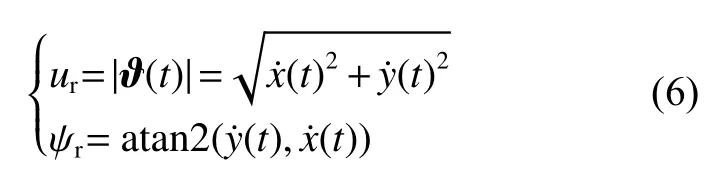
式中：ur为 无人艇的期望速度； ψr为无人艇的期望航向且满足 ψr∈(−π,π]。由于动力学无法直接对航向进行控制，设计如下虚拟控制律：

式中：rr为 无人艇的期望角速度； ψe=ψr−ψ，为航向跟踪误差；Kr为增益常数。

2.2 纵荡速度控制器设计及稳定性分析

在不考虑电机特性的情况下，双桨推进无人艇纵荡速度的响应模型为

式中：fu为纵荡速度方向的不确定项；bu为控制增益。为ESO 子系统的设计和稳定性分析做如下假设。

受模型不确定性和未知环境扰动的影响，式(8)中的fu为未知项。为估计未知项，设计如下一阶线性ESO：

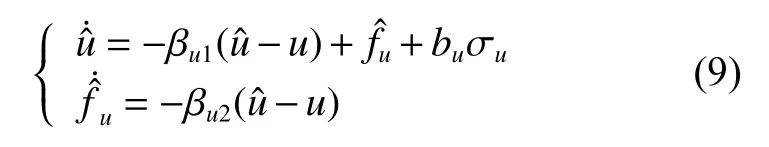
式中， εu∈R， 是一个大于0 的常数；I1是一个三维对角单位矩阵。

根据式(8)，为抵消纵荡速度方向扰动，设计如下纵荡速度自抗扰控制律：

1） ESO 子系统的稳定性分析。

ESO 子系统式(11)的稳定性由引理1 给出。

引理1：在满足假设1 的条件下，式(11)所示系统 状 态 为E1， 系统输入为f˙u的ESO 子 系 统 是 输入状态稳定的。

证明：构建如下李雅普诺夫方程[8]：

对方程(15)进行求导，得

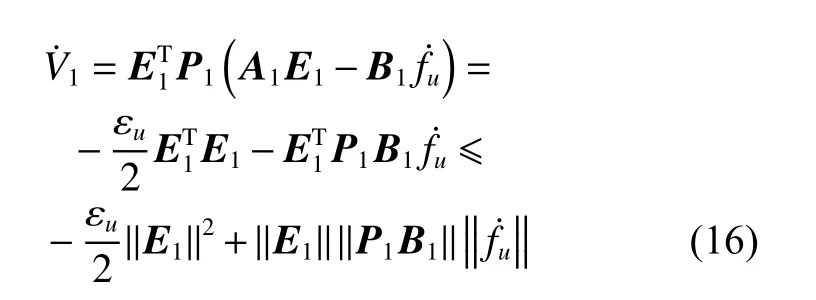
由可得

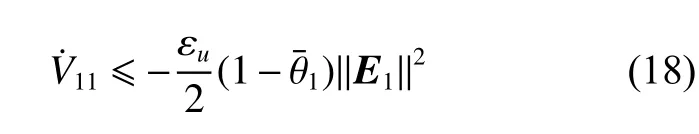
2） 控制子系统的稳定性分析。

控制子系统式(14)的稳定性由引理2 给出。

证明：构建如下李雅普诺夫方程：

对V2求导，得

将式(14)代入式(21)，可得

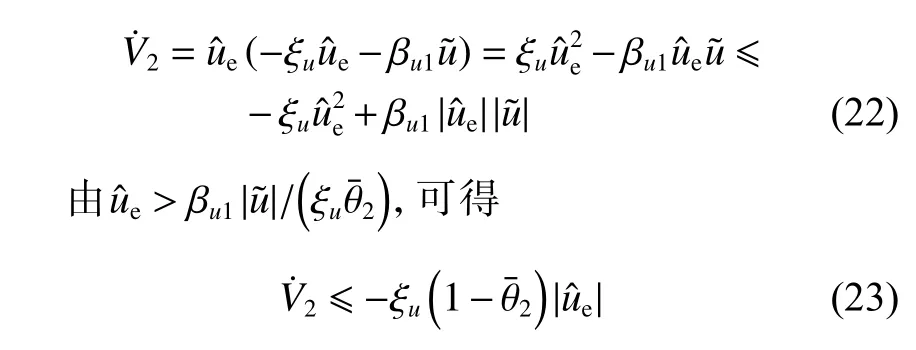
式中， 0 ＜θ¯2＜1。因此，控制子系统式(14)是输入状态稳定的，且存在 KL 类函数 α2和 K∞类 函数 γ2使满足：

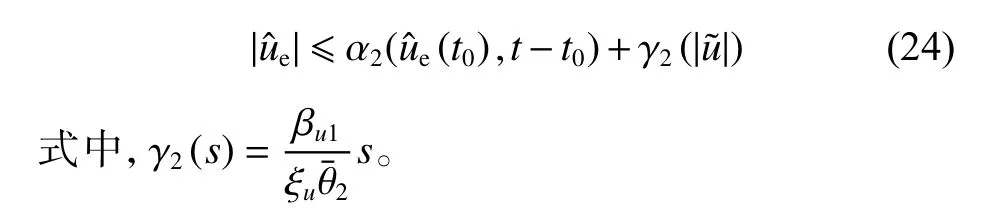
3） ESO 子系统与控制子系统级联稳定性分析。

将ESO 子系统式(11)与控制子系统式(14)看作一个级联系统：

由 Σu1和 Σu2组成的基于ESO 的前纵荡速度控制器级联系统稳定性由定理1 给出。

定理1：考虑无人艇纵荡速度式(8)，在满足假设1 的条件下，纵荡速度ESO 式(9)和纵荡速度控制律式(13)使 Σu1和 Σu2组成的级联系统是输入状态稳定的。

2.3 艏摇角速度控制器设计及稳定性分析

在不考虑电机特性的情况下，双桨推进无人艇艏摇角速度的响应模型为：

式中：fr为 艏摇角速度方向的不确定项；br为控制增益。为ESO 子系统的设计和稳定性分析做出如下假设。

受模型不确定性和未知环境扰动的影响，式(27)中的fr为未知项。为估计该未知项，设计如下一阶线性ESO：

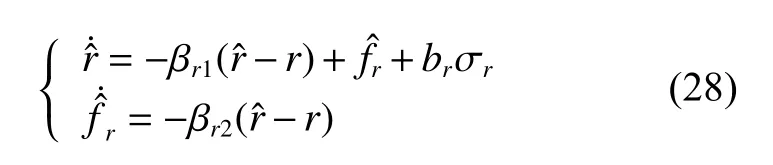
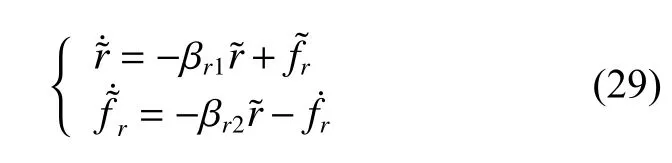
令E3=[r˜,f˜r]T，将式(29)改写成矩阵形式：

式中， εr∈R，是一个大于0 的常数。

根据式(27)，为抵消艏摇角速度方向扰动，设计如下艏摇角速度自抗扰控制律：

至此，整个闭环系统控制器设计完毕，控制器结构如图3 所示。

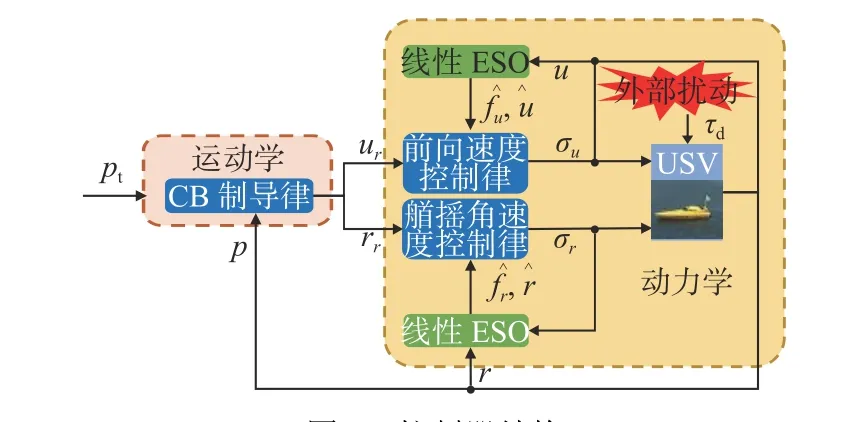
图3 控制器结构Fig. 3 Controller structure

1） ESO 子系统的稳定性分析。

ESO 子系统式(30)的稳定性由引理3 给出。

引理3：在满足假设2 的条件下，式(30)所示系统 状 态为E3， 系统 输 入 为f˙r的ESO 子系 统 是输入状态稳定的。

证明：构建如下李雅普诺夫方程：

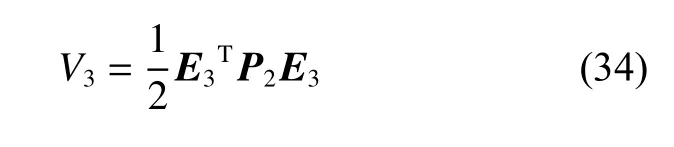
对V3求导，联立式(30)，可得

由

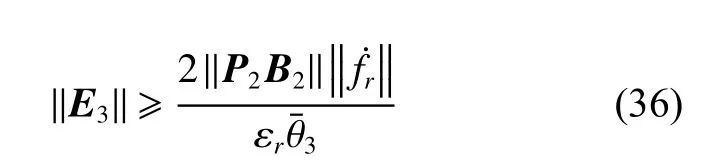
可得

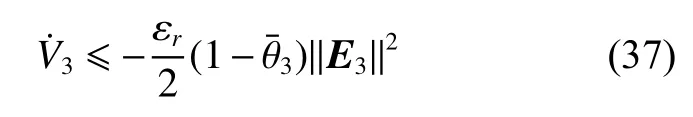
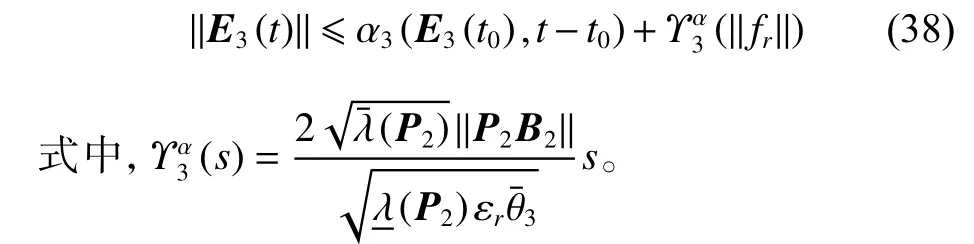
2） 控制子系统的稳定性分析。

控制子系统式(33)的稳定性由引理4 给出。

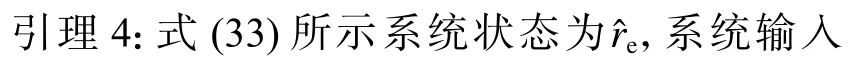
证明：构建如下李雅普诺夫函数：

对V4求导，联立式(33)，可得

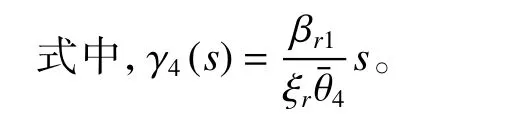
3） ESO 子系统与控制子系统级联稳定性分析。

将ESO 子系统式(30)与控制子系统式(33)看作一个级联系统：

由 Σr1和 Σr2组成的基 于ESO 的艏摇 角速度控制器级联系统稳定性由定理2 给出。

定理2：考虑无人艇艏摇角速度式(27)，在满足假设1 的条件下，艏摇角速度ESO 式(28)和艏摇角速度控制律 式(32)使 Σr1和 Σr2组成的级联系统是输入状态稳定的。

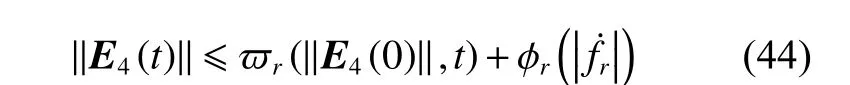
3 试验结果

为了验证本文所提的基于ESO 的平行接近制导抗干扰目标跟踪控制方法的有效性，采用图4所示的2 艘CSICST-DH01 号无人艇进行试验。该无人艇装配有全球定位模块、电子罗盘、运动处理单元、飞思卡尔单片机、无刷直流电机、电子调速器、无线通信模块和电源等设备。

图4 目标跟踪无人艇试验平台Fig. 4 Experimental platform for target tracking of USV

本次试验的控制器参数为：umax=0.7 m/s，δp˜=4，βu1=1， βu2=0.25 ，βr1=1， βr2=0.25，ξu=2，ξr=0.5，bu=1，br=1。为避免跟踪艇和目标艇发生碰撞，根据坐标平移原理，使跟踪艇跟踪目标艇附近的虚拟目标点，虚拟目标点在XE-YE中的位置如下[14]：

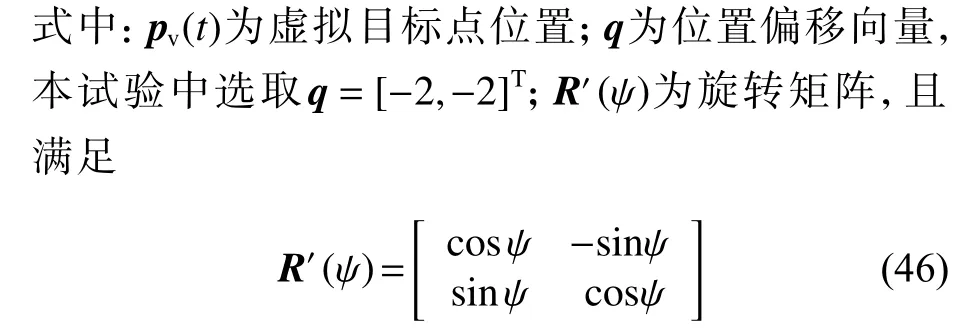
图5～图7 展示了纵荡速度控制试验的结果。图5 表明，对于给定的期望速度信号，基于ESO的估计值和无人艇的实际速度均能在较短的时间内稳定到期望值。图6 显示，在纵荡速度控制律式(13)的作用下，在稳态时，无人艇的速度跟踪误差稳定在0 左右。图7 展示了无人艇在暂态和稳态时的扰动变化情况，在稳态时，扰动基本为恒定值，这与实际情况相符，说明了纵荡速度ESO式(9)的有效性。

图8～图10 展示了艏摇角速度控制试验的结果。图8 表明，对于给定的期望速度信号，基于ESO 的估计角速度和实际艏摇角速度均能在较短时间内稳定到期望值。图9 显示，在艏摇角速度控制律式(32)的作用下，在稳态时，无人艇的角速度跟踪误差稳定在0°左右。图10 显示无人艇在稳态时扰动基本为恒定值，与实际情况相符，说明了艏摇角速度ESO 式(28)的有效性。

图5 USV 纵荡速度Fig. 5 Surge velocity of the USV

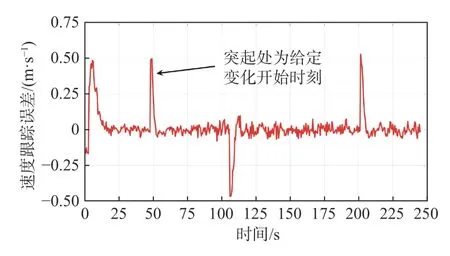
图6 纵荡速度跟踪误差Fig. 6 Tracking error of the surge velocity

图7 纵荡速度ESO 的扰动估计Fig. 7 Estimated disturbance based on the surge velocity ESO

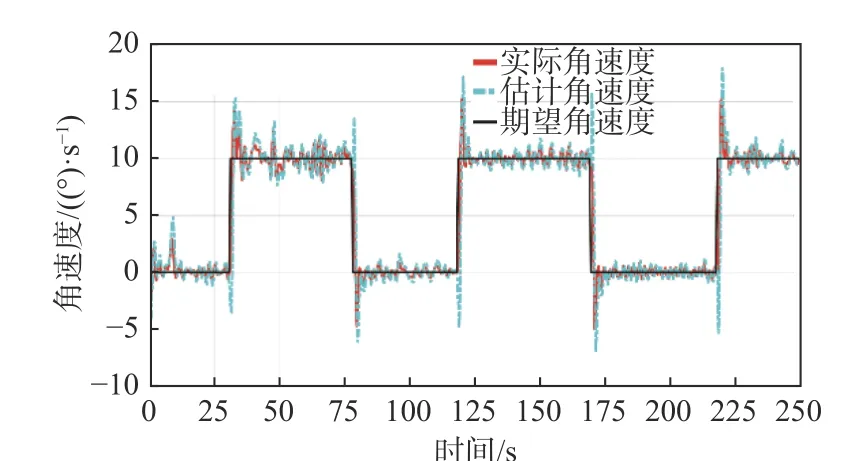
图8 USV 艏摇角速度Fig. 8 Yaw angular velocity of the USV

图9 艏摇角速度跟踪误差Fig. 9 Tracking error of the yaw angular velocity

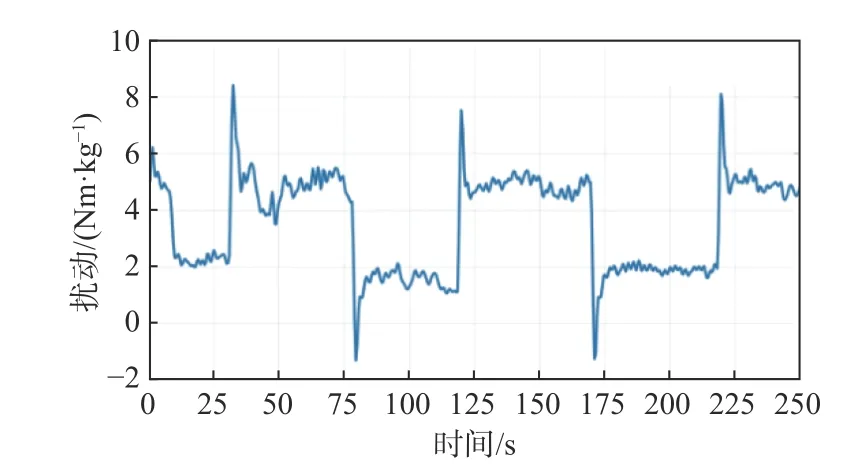
图10 艏摇角速度ESO 的扰动估计Fig. 10 Estimated disturbance based on the yaw angular velocity ESO

图11～图14 展示了艏摇角速度控制试验的结果。图11 显示了跟踪艇（红线）和目标艇（蓝线）的实际轨迹信息，从中可以看出，跟踪艇已稳定至式(45)设定的虚拟目标点位置。图12 展示了跟踪艇与虚拟跟踪点的跟踪误差，从中可以发现，在所提CB 制导律式(6)的作用下，无人艇的位置逐渐收敛至虚拟目标点附近，跟踪误差稳定在0 m 左右。由图13 和14 可知，随着跟踪误差的减小，跟踪艇与虚拟目标点的航向和速度渐趋一致。本次试验湖泊中存在有水草并随机分布于水中。在75 s 时经过水草密集区，由于跟踪艇推进器被水草缠绕，导致误差增大，由制导律式(6)和控制律式(13)可知，纵荡速度开始增加，纵荡速度控制输入 σu也增加，螺旋桨转速增加，摆脱水草后继续追赶目标，使跟踪状态重新回到稳态。

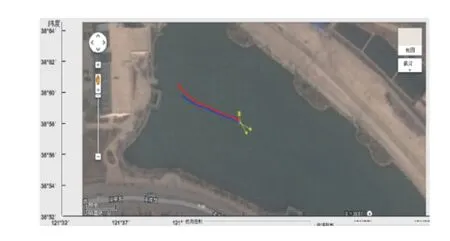
图11 无人艇的目标跟踪轨迹Fig. 11 Target tracking trajectory of the USV

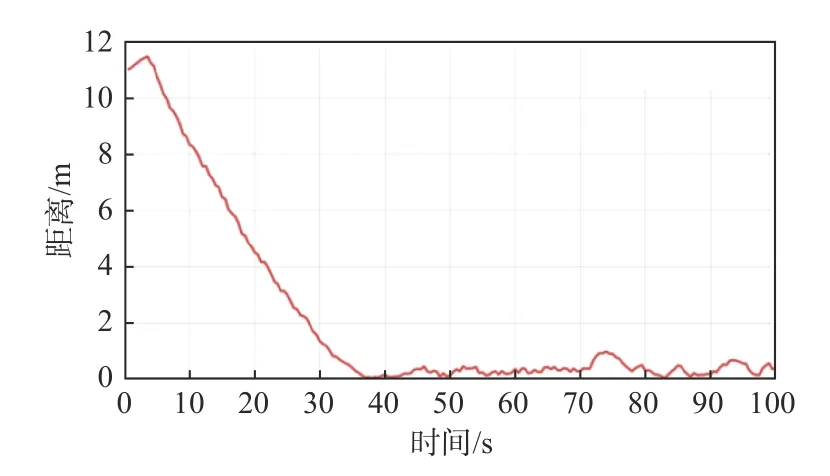
图12 基于CB 制导的跟踪误差Fig. 12 Tracking error based the CB guidance law

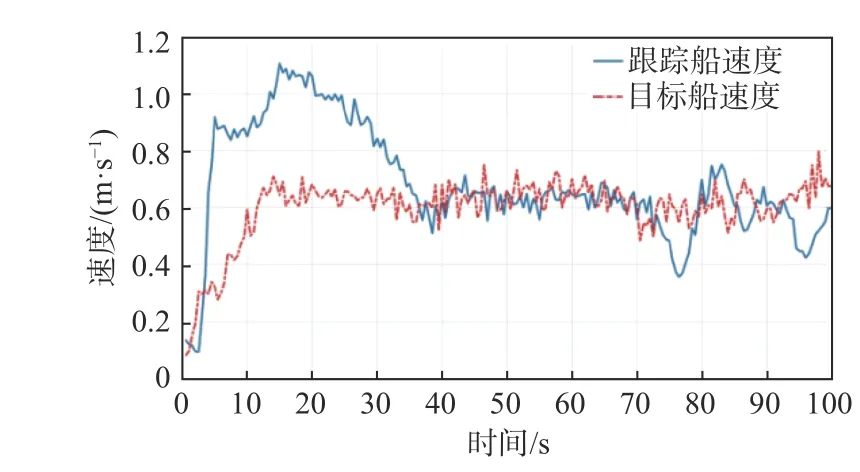
图13 跟踪艇和目标艇的速度Fig. 13 Actual speed of the target ship and follower ship

图14 跟踪艇和目标艇的航向Fig. 14 Actual yaw of the target ship and follower ship

4 结 语

本文针对双桨推进无人艇的目标跟踪问题，提出了基于ESO 的CB 制导抗干扰目标跟踪控制方法。首先，在XE-YE和XB-YB坐标系下建立了双桨推进无人艇运动模型。接着，在运动学层级提出了基于CB 制导的目标跟踪控制律，在动力学层级提出了基于ESO 的纵荡速度控制律和艏摇角速度控制律，克服了无人艇模型的不确定性和由未知环境扰动带来的问题。通过输入状态稳定性定理和级联定理，证明了所提控制器的稳定性。最后，通过试验证明了所提抗干扰目标跟踪控制方法的有效性。