基于参数扰动模型的遥控潜水器滑模控制方法

崔鹏飞，田军委，孙江龙，王轩

1 西安工业大学 电子信息工程学院 西安 710032

2 西安工业大学 机电工程学院 西安 710032

0 引 言

遥控潜水器（ROV）已被广泛应用于水下任务[1]。根据水下作业任务的不同，ROV 需要不断改变其操作工具或拾取和释放导致行为改变的负载。这会导致其重量、浮力和水动力的变化，这些因素会使ROV 控制性能下降[2]。此外，ROV 必须应对以水流和浅水波浪为表现形式的高度动态的水下环境对ROV 控制的影响[3]。当ROV 运动系统的动态特性取决于时间或是其运行条件的变化时，就需要设计一种能改善水流与外界干扰影响的控制器，以提高ROV 的控制性能。

国内外学者对此开展了深入研究。申雨轩[4]讨论了存在海流干扰下的水下机器人模型，采用3 个方向海流的相对流速作为模型的干扰项。但其研究没有考虑到各个方向海流干扰的耦合性，因而很难保证系统的控制精度和鲁棒性。刘慧婷等[5]对水下机器人受到的干扰力，采用非奇异终端滑模控制对推力进行补偿，用来减小水下机器人所受到的干扰力；但研究中未考虑水流的干扰，且其干扰力系人为设定。杨俭健等[6]和杨建华等[7]针对ROV 深度控制系统的不确定性以及外界干扰，设计了滑模变结构控制器来处理环境的干扰力，但系统的鲁棒性只是局限在有界的外部扰动内。Liu 等[8]设计了一种滑模控制器来控制由机械手引起的机器人的俯仰变化并检测摇动和倾斜，通过模糊系统逼近扰动和不确定性。虽然模糊系统具有很强的逼近任何非线性系统的能力，但由于其模糊规则的制定具有一定的不确定性，因此会对控制精度有所影响。Kim 等[9]提出在水下环境大扰动下操作的无人水下机器人自动控制系统，用滑动观测控制器估计了非线性动力学模型的扰动并补偿控制输入以实现稳健的控制性能，在强环境干扰下控制水下机器人，具有估计环境干扰的优点。虽然设计的控制器具有一定的自适应性，但没有对非线性模型的不确定性进行讨论。

综上所述，对于ROV 控制效果不理想的主要原因，一方面是没有建立完整的ROV 模型，另一方面则是设计的控制器在简化模型下对实际系统的控制性能[10-12]不理想。

考虑到外界干扰力与模型不确定性对ROV控制的影响，本文拟在ROV 非线性模型的基础上，考虑建模的不确定性和模型所受干扰的影响，建立新的适应扰动的ROV 非线性模型，设计一种基于参数扰动模型的滑模控制器，以解决ROV 运动控制易受到外干扰和模型不确定性影响的问题。

1 ROV 参数扰动模型

ROV 具有很复杂的非线性特性而且自由度之间的耦合关系也很复杂[13-14]，ROV 在水中不仅受到水的影响，而且还会受到自身模型参数的影响。在对ROV 建模时，这些因素都必须考虑到。ROV 的数学模型是否完整和准确对其控制性能至关重要[15-16]。

1.1 坐标系与运动参数

空间刚体具有6 个独立的运动变量：在空间三维方向的平动和转动。空间坐标系是描述ROV 运动的基础，选取合适的空间坐标系来描述ROV 的运动可以极大地简化表述ROV 的运动学与动力学模型。本文为ROV 建立了2 个坐标系，惯性坐标系（E−ξηζ）及ROV的本体坐标系（O−XYZ）。2 个坐标系都按照右手法则来确定相应的方位，图1 所示为ROV 的2 个坐标系。在坐标系下定义的ROV 运动参数如表1所示。

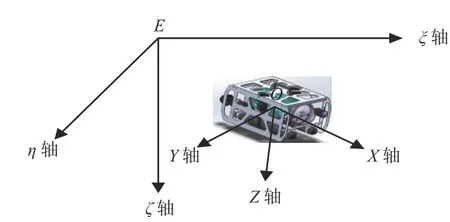
图1 ROV 的坐标系Fig. 1 Coordinate system of ROV

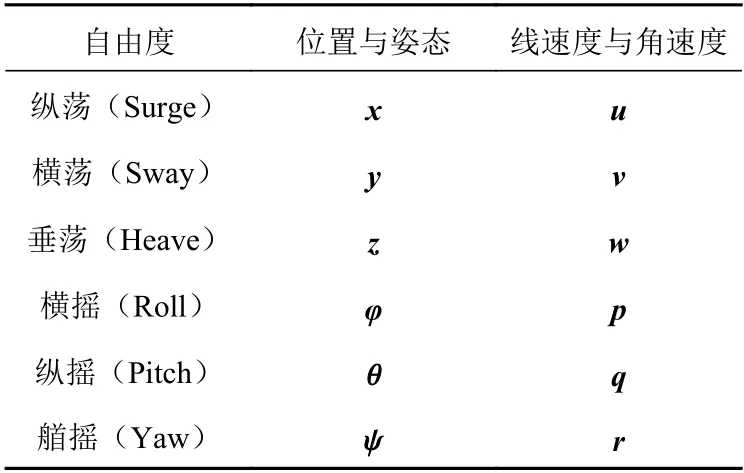
表1 ROV 的运动参数Table 1 Motion parameters of ROV

1.2 ROV 动力学模型

ROV 的动力学模型是用于分析其在水中复杂工况下的受力情况。ROV 在水下受到多种力的作用，主要有流体动力（惯性类水动力和黏性力类水动力）、静力（重力与浮力）、推进器的推力以及受到的外界干扰力和缆线力等，如式（1）[17]所示：式中： τH为ROV 在水下受到的惯性类水动力和黏性类水动力； τR为ROV 在水中受到的静力（重力和浮力）； τP为ROV 推进器的推力 以 及 推 力 矩；f为ROV 外界干扰、水流、缆线力等。

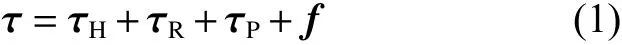
ROV 的一般运动可以在惯性坐标系下进行描述，并且可以用更简化的形式[18]表示为

1.3 参数扰动模型

ROV 动力学模型的参数扰动模型可表示为

式中：pf为模型扰动参数；Δ为模型的不确定性。从模型的扰动参数可以看出参数扰动模型不但有模型参数的不确定性而且包含环境的外干扰。这些参数不确定性和环境的干扰力并非线性不变的，通过软件模拟和施加干扰并与标准的ROV模型比较，就可以确定出ROV 的参数扰动模型。

根据状态变量和模型参数的运动学变换转化为惯性坐标模型。在惯性坐标系下的ROV 模型为

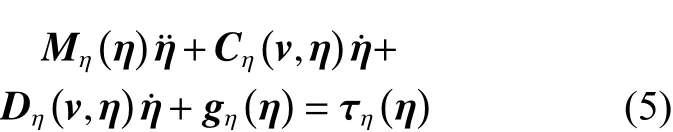
其中：

ROV 的惯量矩阵、向心力和科氏力矩阵以及对角水动力阻尼矩阵参数允许在式(8)和式(10)中规定的范围内变化。假定这些变化是由于建模中参数的不确定性和ROV 外部环境发生变化造成的。利用计算机辅助设计软件Pro-E 通过改变各推进器、ROV 本体框架的质量特性和加入干扰，以及多次模拟水下环境，可以得到不同的惯量矩阵、向心力、科氏力矩阵以及水动力阻尼矩阵。从而计算标准模型的参数矩阵和新的参数矩阵之间的差异，可以确定ROV 参数矩阵的扰动极限。其中，惯性矩阵的扰动极限由其逆矩阵给出

Mη(˙η,η)−1的极限范围为

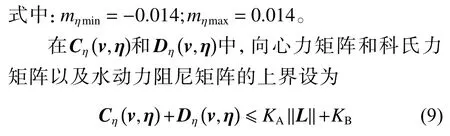
式 中：KA=KB=0.006；L=[ee˙]T，其 中e为 误 差。KA＞0 和KB＞0 为常数，由CAD软件Pro-E 获得，其意义是多次模拟得出的扰动极限模型的2 个参数。

1.4 基于参数扰动的ROV 解耦合

ROV 水下运动时会出现耦合现象，自由度间的耦合会严重影响ROV 的稳定运行。ROV 的速度越大，各自由度间的耦合程度也越大。解决这种耦合现象的一种方法就是对其模型进行解耦。

一般的解耦方法除了忽略自由度间的耦合关系外，还有一个缺点就是没有考虑模型参数的不确定性[19]。本文是在ROV 参数扰动模型的基础上，对ROV 运动模型进行解耦。这种在扰动模型上解耦出来的运动方程既可以让ROV 模型更简化，还包含了耦合现象与环境外干扰的影响。

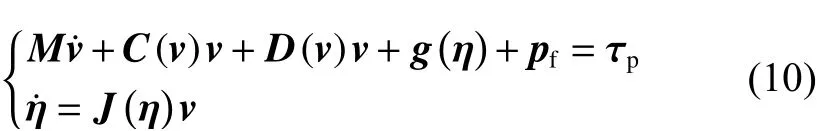
ROV 在运行过程中，要保证潜水器在水下进行正常的平稳运动，ROV 的横摇与纵倾需要为0 或者非常小。所以在设计ROV 时，使其重心与浮心在同一点上，这样就可以保证ROV在水平运动时具有一定的稳定性。根据ROV 的设计思路，可以假设ROV 的横摇角与纵倾角为

将式(11)代入式(10)中，则带参数扰动的ROV 六自由度动力学方程展开可以得到深度方向的运动模型为

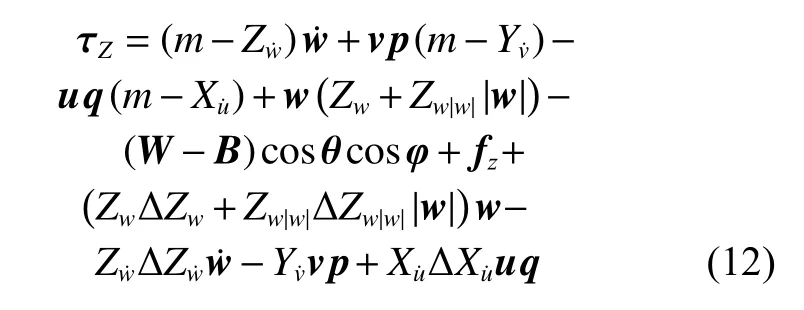
式 中：m为ROV 的 质 量；Xu˙，Yv˙，Zw˙，Zw，Zw|w|均 为ROV 的水动力系数；fz为ROV 在定深方向所受的外力；W和B为ROV 的重力与浮力。

将式（12）变换为

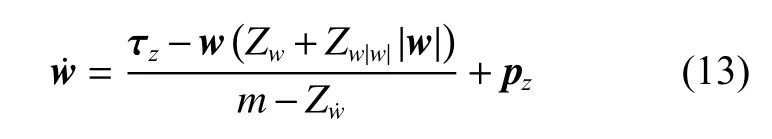
可得到定深的运动方程：

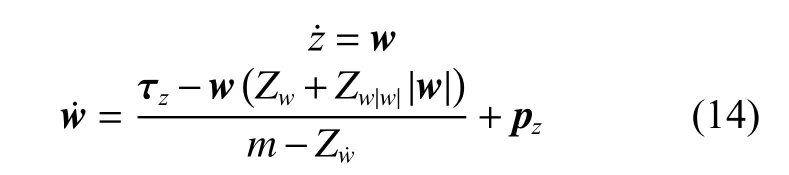
其中：

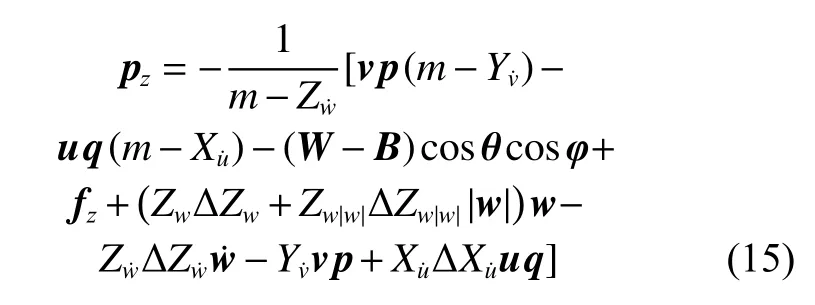
从定深运动方程可以看出，这种方法将耦合项、模型不确定项和外力干扰一起当作外干扰项来考虑，既可以简化模型的复杂度和耦合现象，方便后续设计合适的控制器，也能够最大程度上考虑模型参数不确定性对系统的影响。

2 定深滑模控制器设计

定深方向的运动方程为

为了方便设计控制器，式（16）可写为

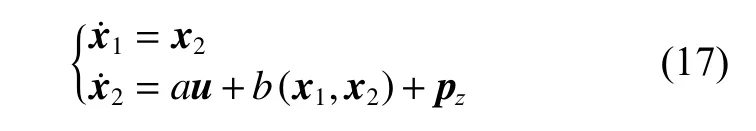
式中：x1=z,x2=w,u=τz；a=1/(m−Zw˙)；b(x1,x2)=[w(Zw+Zw|w||w|)]/(m−Zw˙)。

设理想状态目标为xd，定义误差为

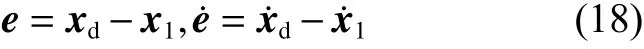
设计滑模面s=ce+e˙，式中，c＞0 满足Hurwitz条件，则

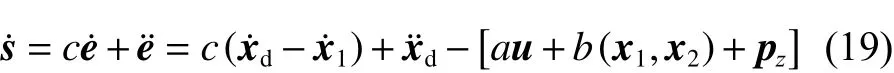
趋近律f(s)=−ksgn(s)，则滑模控制的控制律为

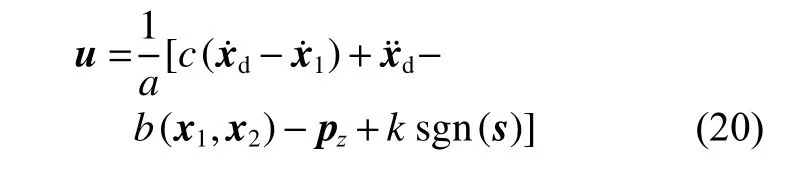
式中：c，k分别为滑模控制器的参数。

选取以下Lyapunov 函数进行稳定性分析

对式（21）求导，得

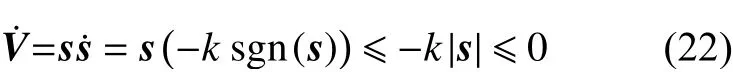
即控制系统稳定且是收敛的。

3 仿真与分析

如图1 所示，本文研究的对象为小型框架式ROV，重量为17.53 kg，长、宽、高分别为0.52，0.46，0.3 m，航速小于1 m/s。此ROV 的重心与浮心在同一点，在水中具有较大的稳定性。

3.1 ROV 模型仿真对比

为了对比带参数扰动模型与标准模型ROV的操纵性，设定ROV 初始轴向位移（纵荡方向）为0 m，初始速度为0 m/s，期望的轴向位移为1 m。在扰动极限mηmax=0.014，KA=KB=0.006，L=[ee˙]T时，对标准ROV 模型和带参数扰动的ROV 模型进行了仿真对比，仿真结果如图2 和图3 所示。

图2 所示为轴向运动1 m，标准ROV 模型与带参数扰动ROV 模型的位置与姿态对比曲线，图3 所示为其速度与角速度对比曲线。由图2(a)与图3(a)可以看出，2 种模型都达到了期望的轴向位移，在带参数扰动ROV 轴向运动中的超调量为0.009 4 m, 系统在148.2 s 时达到稳定，稳定后的误差为0.004 7 m。而标准模型轴向运动的超调量为0.001 6 m，系统在118.43 s 时达到稳定，稳定后的误差为0.000 6 m。结果表明，加入参数扰动的模型对ROV 的操纵性有较大影响，且横荡(图2(b))和艏摇(图2(f))自由度均未能收敛，即在扰动模型下的ROV 不能稳定运行。

3.2 定深滑模控制仿真

为了验证基于扰动模型ROV 定深滑模控制器的性能，设定ROV 初始深度为0 m，初始速度为0 m/s，期望的下潜深度为5 m。模型的扰动极限设为mηmax=0.014，KA=KB=0.006，滑模控制器的参数c=5，k=11。在Matlab 中对扰动模型下ROV的滑模控制器进行了仿真，如图4 与图5 所示。

图4 所示为在惯性坐标系下ROV 滑模控制定深运动5 m 的六自由度阶跃响应图。图5 所示为ROV 定深运动5 m，本体坐标系下ROV 线速度与角速度变量的变化。仿真结果表明，滑模控制器在定深(下潜方向)控制中的超调量为0.011 m，系统在35.4 s 时达到稳定，稳定后的误差为0.009 m。在所期望的深度，所设计的滑模控制达到了运动稳定，在极限扰动模型下也有很好的控制性能。

3.3 定深控制仿真对比

在扰动模型下，设定ROV 初始深度0 m，期望下潜深度5 m。滑模控制器的参数c=5，k=11，PID控制器的参数为Kp=9，Ki=0.15，Kd=2。在Matlab中对滑模控制器与PID 控制器进行仿真，仿真结果如图6 与图7 所示。

图6 为在扰动模型下的PID 控制器与滑模深度控制的对比曲线，图7 为2 个控制器深度控制的速度对比曲线。仿真结果表明：PID 控制响应时间为26.3 s，比滑模深度控制响应时间少；但是PID 控制的超调为1.82 m，与滑模深度控制相比存在较大的超调并且达到稳态的时间很长；而滑模在定深控制上具有很平滑的曲线，基本上没有超调，达到稳态的时间比PID 要早很多。设计的滑模控制器在扰动模型下有更好的控制性能。

图2 标准ROV 模型（绿色虚线）与带参数扰动ROV 模型（蓝色实线）的位置与姿态变量对比Fig. 2 Comparison of position and attitude variables between standard ROV model (green dotted line) and ROV model with parameter disturbance (blue line)

图3 标准ROV 模型(绿色虚线）与带参数扰动ROV 模型（蓝色实线）的速度与角速度变量对比Fig. 3 Comparison of speed and angular velocity variables between standard ROV model (green dotted line) and ROV model with parameter perturbation (blue line)

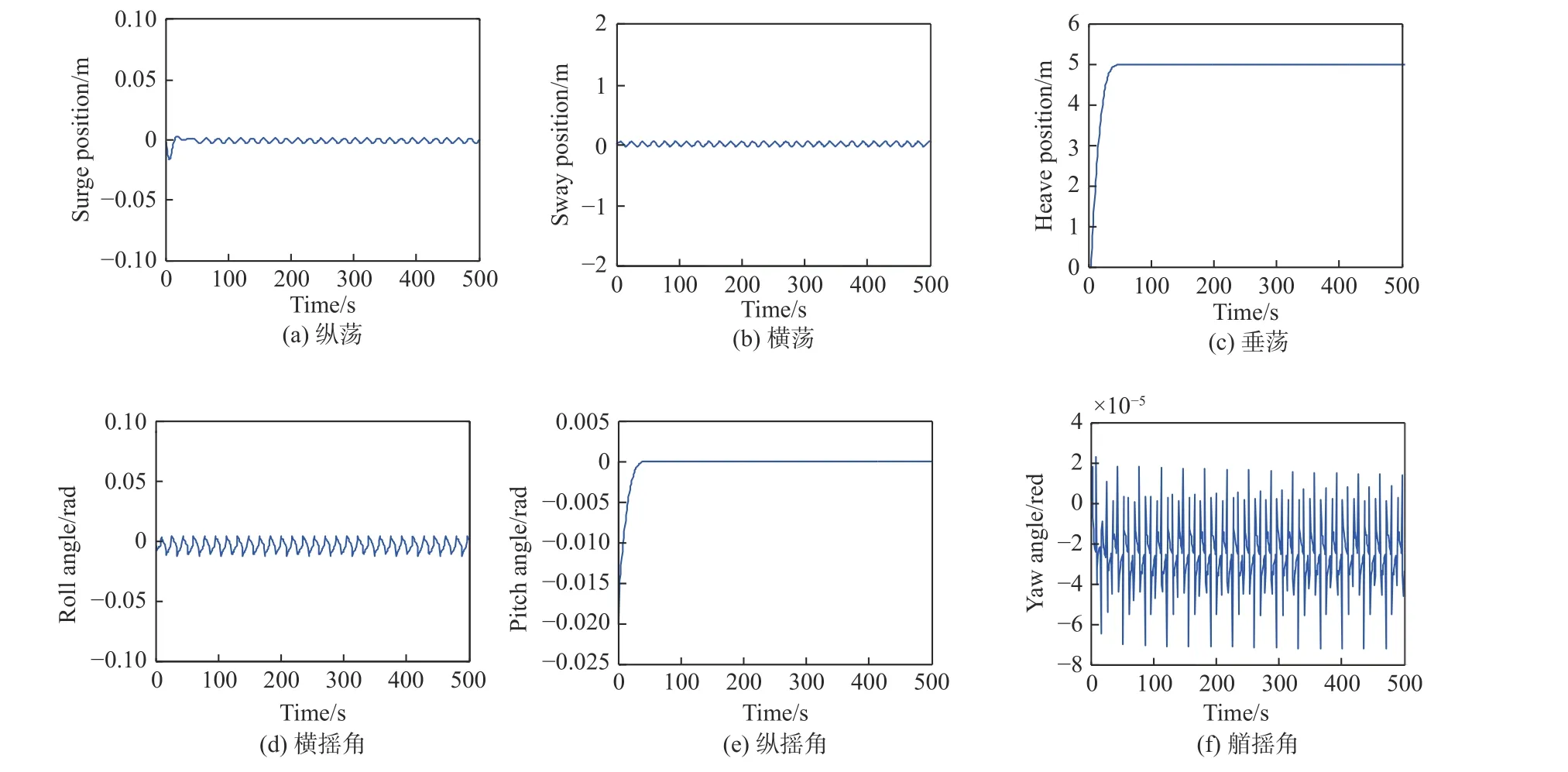
图4 位置与姿态响应Fig. 4 Position and attitude response

图6 PID 与滑模深度控制对比Fig. 6 Comparison of PID and sliding mode depth control

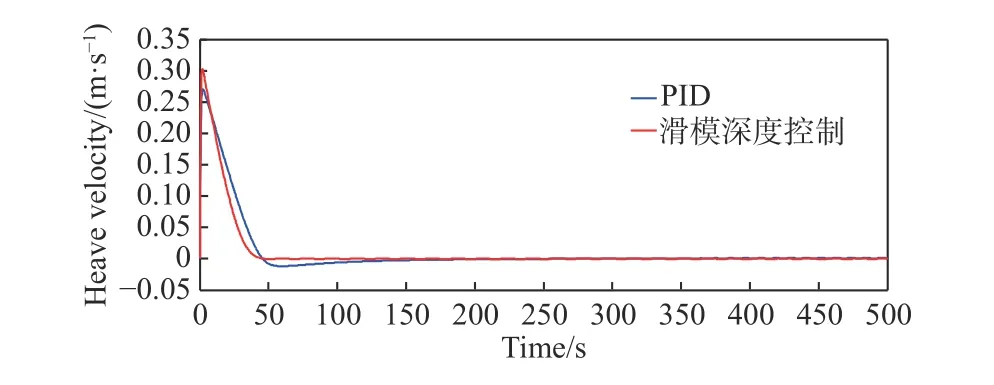
图7 PID 与滑模深度控制速度对比Fig. 7 Speed comparison between PID and sliding mode depth control

4 结 论

本文建立了适应外干扰和模型参数不确定性的带参数扰动的ROV 模型，并且在此ROV 模型上为定深运动设计了滑模控制器，得出了以下结论：

1） 建立的参数扰动的ROV 模型考虑到了外干扰与模型不确定性的影响，有利于提高ROV 的控制效果。

2） 与PID 相比，所提出的基于参数扰动模型的滑模控制器的控制精度高，且基本无超调，提高了ROV的控制性能。

未来还会将所提出的滑模控制器应用于实际工程系统。