混合动力汽车氢镍电池建模研究

徐钦赐， 贠海涛， 杨腾盛， 周哲义

(青岛理工大学机械与汽车工程学院，山东青岛266520)

现阶段等效电路模型有很多种，本文选择的是二阶RC带滞回效应的等效电路模型，该模型可以很好地对应氢镍电池的外特性。从图1 可以看出氢镍电池的滞回特性比较显著，其滞回效应远比一些锂电池要明显。文献[1]介绍了产生滞回的原因，所以无论是在荷电状态(sate of charge, SOC)估算还是等效电路参数辨识，都需要考虑滞回电压这一影响因素。文献[2-5]也给出了不同的滞回电压估算方法。本文的主要思路就是将滞回电压与SOC 进行拟合，实时地估算出滞回电压。参考文献中进行数据的分析和辨识都需要进行脉冲充放电实验来获得数据，然后再进行下一步的工作。本文则是将实车运行1 h 53 min 采集到的电压、电流、时间数据进行辨识，车辆在道路上行驶时任何工况都是随机的，所以采集到的数据即是电池在道路上的真实反映。仿真结果显示利用实车运行工况数据并结合本文提出的估算方法一样可以获得较高的精度，且数据获取将会更加的方便快捷，不需要一些特定的仪器以及特定的工况来获取数据。另外电池内部存在电化学极化和浓差极化，且二者的反应时间差距较大，文献只是将二者进行了简单的介绍，并没有进行细致的研究和分析这两个动态反应过程。本文对两个反应时间分别进行考虑，并且针对反应时间的快慢[6-7]分别辨识出不同时间的模型参数，该方法能够更加体现出电池真实的动态反应[8]。

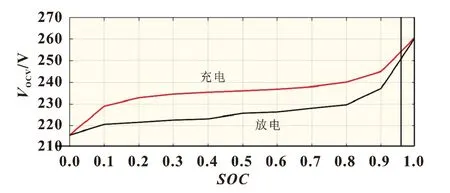
图1 静置3 h的氢镍电池开路电压与SOC的关系

1 氢镍电池的开路电压特性

图1 是通过将氢镍电池进行间歇性的充、放电，然后再静置3 h 后采集电池开路电压。根据氢镍电池的特性分析，静置3 h 后，氢镍电池基本处于稳定状态。

从图1 可以看出，在同一SOC 时刻下，充电的开路电压远远高于放电的开路电压，这就是氢镍电池的滞回特性。估算氢镍电池的SOC 状态时，如果不考虑氢镍电池的滞回特性，精度将会大大降低，本文在第4 节进行数据分析时会对比考虑滞回和不考虑滞回仿真精度的差异，同时迟滞现象也改变了电池的模型参数，从而改变了电池的动态响应。所以在参数辨识时需要考虑滞回因素，参数辨识是电池SOC 估算的基础，辨识结果的精度直接影响SOC 估算的精度。本文对于滞回的考虑是建立一个实时在线估算系统从而判断选择哪种工况的电压，当电池充放电循环次数较多时，电池会出现老化的因素，会间接影响到估算的精度。由于在本文中没有考虑电池老化对电池特性的影响，所以滞回特性不会随着电池的老化而改变，考虑老化因素对电池特性的影响将会是下一步重点的研究工作。

2 氢镍电池等效电路模型

等效电路模型的精度随着电路模型阶数的增多而提高,但不是越高越好，因为模型阶数越高，辨识过程就越复杂，所以实用性并不好[8]。本文综合考虑模型的精确性与复杂性以及实用性，故选用的模型为考虑滞回特性的二阶RC 等效电路模型。图2 为二阶RC 等效电路模型。该模型可以很好地体现出电池的特性[9]，R0表示电池的欧姆内阻；并联的R1、C1表示电池的电化学极化；并联的R2、C2表示电池的浓差极化；Vh表示电池的滞回特性；EEMF为电池的平衡电势；VOCV表示电池开路电压；V0表示负载电压。

根据图2 可以得到模型输出的电池端电压数学表达式：

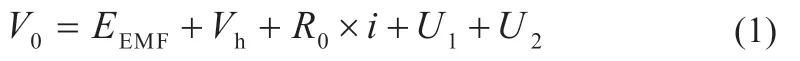
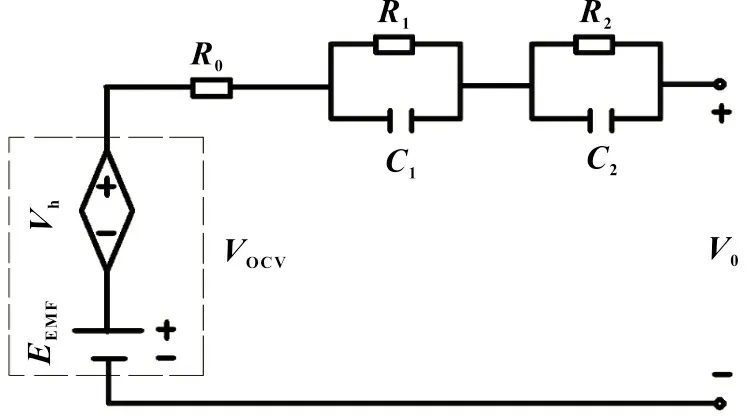
图2 二阶RC等效电路模型

3 模型参数辨识

根据氢镍电池的外特性表现可知，电池的欧姆内阻上的电压反应时间和电化学极化的反应时间τ1都比较短暂，而浓差极化反应时间τ2比较长，在文献[10-11]中只是介绍了这两个时间常数，并没有根据具体的时间长短情况进行具体的分析。常用的参数辨识方法一般都是采用最小二乘法或者递推最小二乘法以及运用扩展卡尔曼等方法进行参数的辨识，这些方法将τ1、τ2一起考虑进行运算，从而得到辨识出的参数，但精度不是很高，辨识出的参数精度直接对后期SOC 估算的准度有很大的影响。为了克服这个缺陷，本文针对电池快速动力学反应和慢速动力学反应的特性，提出一种新的参数辨识方法，将反应时间长、短不同的参数进行单独的考虑从而辨识出等效电路中的参数。同时因为氢镍电池的滞回特性比其他类型的动力电池明显，所以在分别考虑时间常数的前提下，首先考虑电池的滞回特性，因为氢镍电池的滞回反应也影响了电池的模型参数精度，从而改变了电池的动态响应。

将开路电压定义为：

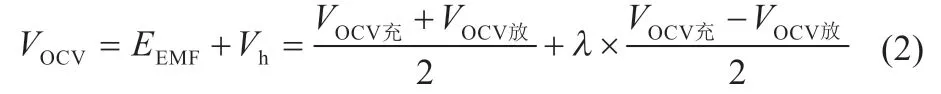
当为充电工况时，λ 为1，当为放电工况时，λ 为-1，在Simulink 模型中自动判别为何种工况。将滞回电压Vh与SOC的状态进行曲线的拟合，随着SOC 的改变，实时计算滞回电压，所以SOC 估算的精度极大影响着滞回电压的精度，而SOC 的精度主要受到辨识参数精度的影响，分开研究两个反应时间长短的参数，可以更精确地辨识出参数，进而可以更加精确地估算出电池的SOC。

负载电压的表达式为：

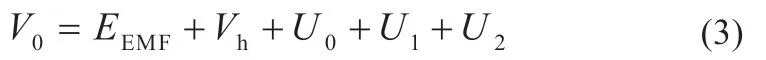
RC 模块电压可以表示为：

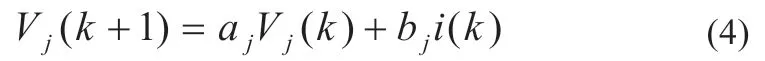
式中：aj= exp(- Ts/ τj)； bj= Rj(1 - aj)； j =1,2；Ts为采样间隔时间；Vj(k)表示Vj在k 时刻的电压。

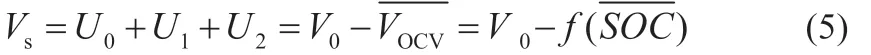
令：将方程(3)与(5)结合：

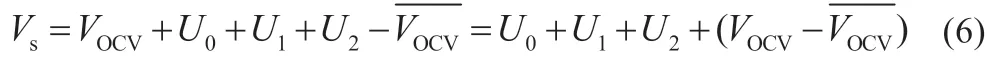
假设：

式中：Va为开路电压差。

模型误差：

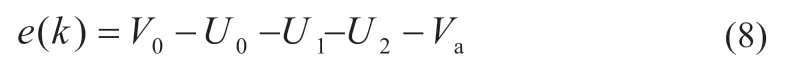
快速反应的电压：

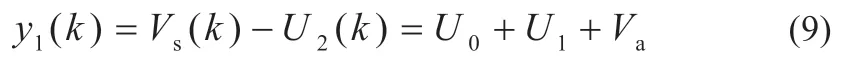
慢速反应的电压：

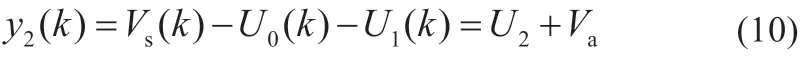
慢速反应参数采用最小二乘进行辨识：

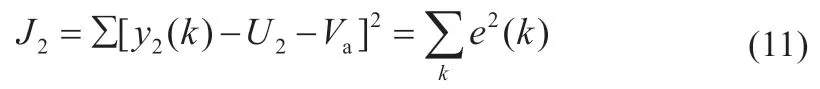
快速反应的参数采用遗忘因子β 为0.98 的递推最小二乘进行辨识：

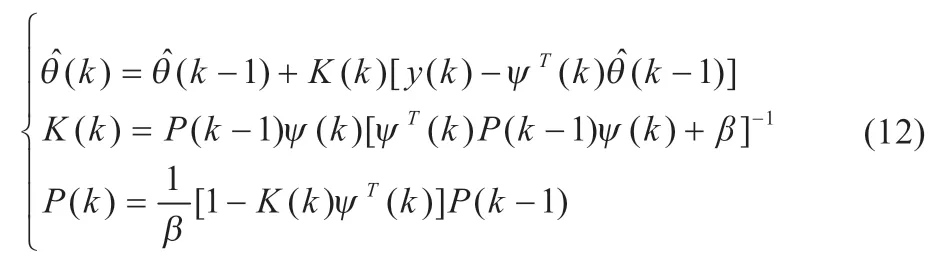
等效电压源部分的数学关系可表示为：

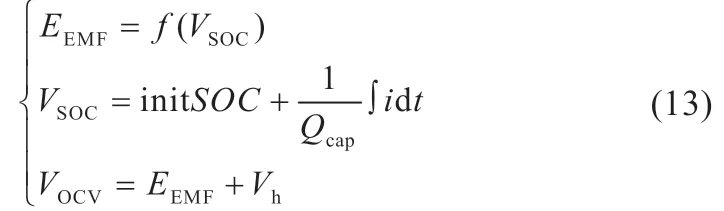
式中：Qcap为电池容量。

在等效阻抗电路部分的数学关系可表达为：

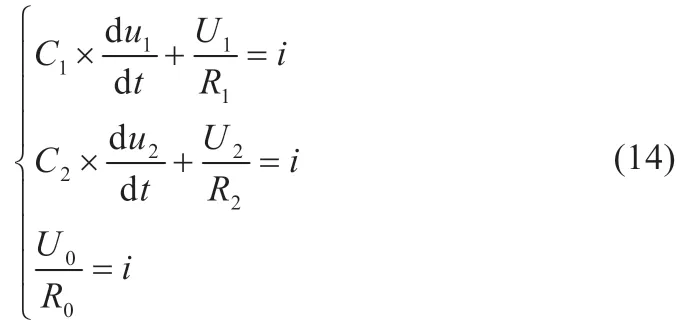
将式(13)与(14)的数学表达式在Simulink 中实现，即得到本文的模型仿真结构图。本文将构图分为两个部分，充电部分和放电部分，设置判断电流的正负来进行模型的实现。

4 模型的验证

在本文中采用的数据为车辆实际运行过程中采集到的电压、电流和时间，采集数据时，室外温度为15 ℃，温度升高变化范围在5～7 ℃，所以本文建立的模型适用温度范围为15～22℃，如图3 所示。

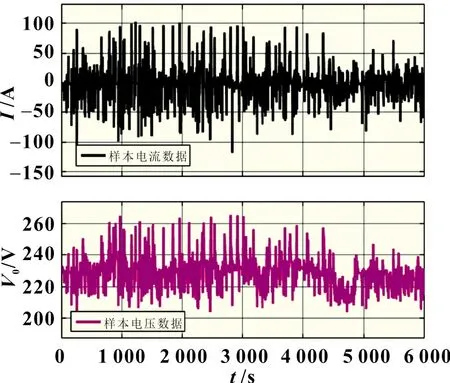
图3 参数辨识所用到的样本数据

为了能够更加精确地体现动力电池的特性，所以选取的数据为电池在运行中只有充电和放电两个时间段分别进行分析，并对这两个时间段分别考虑电池的快速反应电压和慢速反应电压，从而辨识出电池的参数。因为本次辨识采用的数据为车辆实际运行采集到的数据，所以辨识的结果可以很好地适应实车运行的工况。图4所示为放电工况相关样本数据。

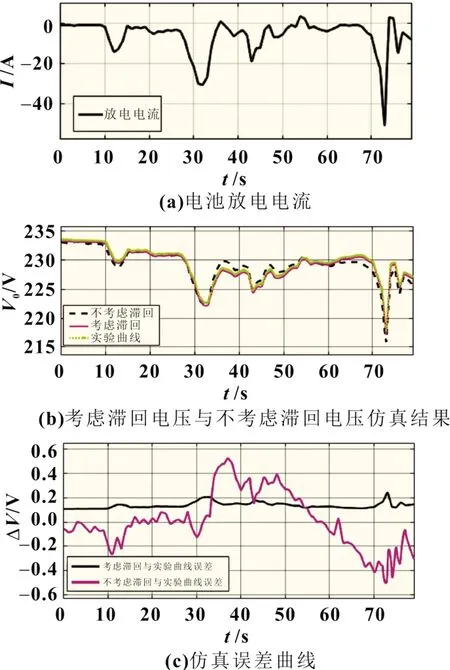
图4 实车放电79 s，仿真曲线与实验数据曲线对比结果

从图4 可以看出，采用新方法进行仿真与真实值曲线相比具有较好的拟合效果，但是还是存在一些误差，这是由于氢镍电池的滞回现象没有考虑。从图中可以看到加入滞回特性以后，仿真曲线的精度更高，平均仿真误差值低于0.01 V。图5 为充电工况相关样本数据。

从图5(a)可以看到，充电电流数据里也夹杂着一些放电电流，因为该动力电池在运行中，充放电工况一直在交替循环，没有很长时间充电或者很长时间放电的工况，所以本文在选取充电工况数据时，尽可能的多选取一些充电时间比较多的数据，来保证辨识结果的精准性。从图5 可以看出，带滞回效应的仿真曲线与实际数据曲线可以很好地吻合，且仿真精度较高，其平均仿真误差值也低于0.01 V，验证了该方法的可行性。

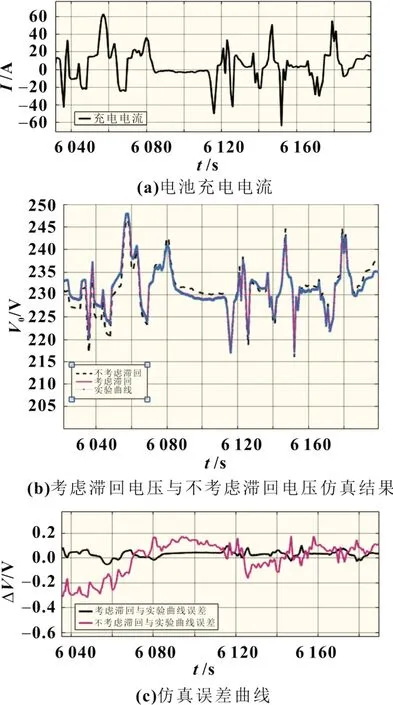
图5 实车充电170 s，仿真曲线与实验数据曲线对比结果

接下来通对辨识结果进行仿真，通过与车辆实际运行的数据进行比较，验证模型的精度。图6 为实测电压与仿真结果的对比情况,图7 为车辆运行在高速工况下的样本数据与仿真结果对比情况。通过仿真图形可以看出，运用本文提出的方法可以很精准地追踪到车辆实际运行的数据，具有较高的准确性。

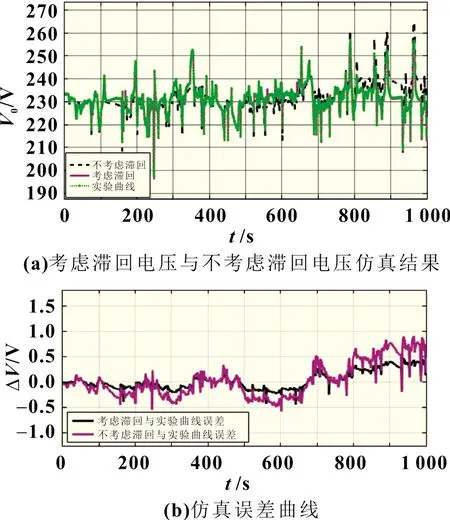
图6 仿真结果与实测电压的比较

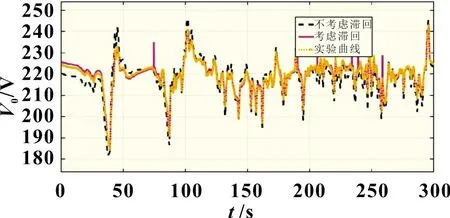
图7 在高速工况下考虑滞回电压与不考虑滞回电压仿真结果

5 结论

(1)本文首先建立了二阶的带有滞回特性的等效电路模型，然后根据电池的动态特性对电池内部的快速反应和慢速反应分别进行考虑，从而分别辨识出等效电路模型的参数，经过验证表明，辨识结果精度比较高。

(2)本文所选取的数据为车辆实际运行1 h 53 min 所收集到的电流电压数据，从而不用专门进行电池充放电实验。为了保证精度，本文不仅分别考虑了慢速和快速反应，而且还在两个反应的基础上考虑了电池充电和放电这两个工况，最大程度上保证辨识的精确性。通过对比结果可知，该模型和本文提出的方法具有较高的实用性和经济型，并且该方法可以随着氢镍电池的老化等因素，自动在线辨识出适合该时刻的电阻电容等值，具有一定的时效性。

(3)参数和电压的初始值都是任意设置的，但是仿真曲线可以在很短的时间内逼近真实值，有比较好的收敛性。

(4)本文在采用充电和放电工况进行分析时，充电工况里有一些放电动作。同样的，放电工况里也有少许充电动作，可能会对辨识结果产生一些影响。因为车辆运行中，任何动作都是随意的，没有专门针对分析研究进行的专门充电或放电动作，下一步应测量一些专门针对本次研究方法的数据进行深层次的分析验证。

(5)本文没有考虑电池温度变化情况对电压的影响，下一步的研究应该考虑温度变化对电压的影响问题。