冻融对严寒地区湿地软土路基累积应变影响

崔高航, 张玳笠, 朱成浩, 席 晨

(东北林业大学土木工程学院, 哈尔滨, 150040)

严寒的哈尔滨地区冬季长达6个月有余,1月份平均气温在-15～-30 ℃[1]。该地区路基土也随着季节的变化历经周期性的冻融循环作用,导致路基土的力学性质、物理性质发生较大的损伤。路基温度低于0 ℃时,土壤中水分会因热力学条件改变而发生相变和迁移。水冻结成冰体积膨胀,对土体有明显挤压作用,破坏土的原有结构,对道路路基土的质量以及结构性造成影响甚至破坏。其中湿地软土路基因含水率较高而受冻融影响更为明显。

对于路基土动力学的研究,中外皆有不同研究方向及研究进展。Tang等[2]、Li等[3]对上海地区地下隧道施工的冻融饱和软黏土的动力特性进行研究,提出了适用于该地区冻融饱和软黏土动应力应变关系的双曲线模型。Hyodo等[4]研究发现:原状土动强度曲线会因固结压力的增大而愈发趋于稳定；陈颖平等[5]对萧山原状土进行动三轴试验验证了此类现象,提出土体最小动强度这一概念,并且证实了当振次N大于1 000 时,在不同应变破坏标准定义下,土体动强度曲线较为接近并最终趋于一致。戴文亭等[6]按照粉质黏土动强度与冻融循环之间的关系建立了动强度衰减模型,阐述土体动强度会随着冻融循环作用而逐渐减弱。Christ等[7]在冻结状态下对土的阻尼比及其相关影响因素进行了分析。Shelman等[8]主要研究在循环温度(20～-23 ℃)下的5种不同土类的应变变化率和弹性模量。

近年来有关寒区土动力特性方面的研究主要集中在对重塑土的动强度、动弹性模量等,但对受冻融循环作用下的路基原状土,尤其是受动荷载作用后的累积塑性变形研究却不够完善。相关工程中仍采用重塑后的未冻土计算模型来预估路基土受动荷载作用所引起的沉降。但大量文献已表明:土经冻融后的动力学参数与原土样相比有明显衰减；重塑土与原状土相比,实验所得累积应变值偏小等。且因所处地区的差异,各实验使用的土类也有所不同。湿地路基软土土质松软,在同等受力条件下的变形量、沉降量、累积应变等皆大于其他地区。更何况湿地软土含水率较高,致使该地区受反复冻融循环影响程度较大,土体结构易发生不规则变化,在受动荷载作用后便会出现不同程度的塑性形变。若无法正确预估道路通车后规定年限内的变形量,则道路的平整度就无法得到保障,进而致使交通事故的频发。因此,现对不同冻融循环影响下的路基原状土进行动三轴试验,探究其累积变形量的相关变化规律,以期得到更合理的方式来预估寒区湿地软土路基原状土的累积应变,为今后实际工程进行动荷载变形分析计算提供合理可靠的理论基础。

1 动三轴试验

1.1 试验土样

试验依托绥满高速卧白项目A1标段,试验土样采用ZK626-ZK628直填段路基原状土。该路段位于哈尔滨市与大庆市之间,横穿湿地,水位较高。试验取土点位于路基中间带正下方,取土深度均在冻结层以内。土样的基本物理参数如表1所示。

表1 试验土样的基本物理参数Table 1 Basic physical parameters of test soil samples

1.2 试样处理

1.2.1 真空饱和

如图1(a)所示,将原状土置于切土盘上切取直径39 mm,高80 mm的圆柱土样，制成土样后放入饱和器贴好标签。按《公路土工试验规程》(JTG E40-2007)步骤,将装有制成土样的饱和器放入真空缸内,注入蒸馏水淹没饱和器,在-101 kPa下静待24 h后取出，以确保饱和度达到95%以上。

1.2.2 冻融循环

土样经真空抽气饱和后，为防止水分蒸发,用保鲜膜密封后,置于土工实验室温控冻融箱中。现有研究[9]表明，气温对地温的影响具有滞后性,路基土冻结所需时长略大于融化时长。综合考虑土样所处地区的平均温度,使得土样充分冻结。试验设置从恒温18 ℃开始,每小时降温6 ℃,降至-18 ℃后静置8 h,再升温至18 ℃放置10 h,此为一次冻融循环。每次冻融循环试验放置两个参照样，如图1(b)所示,分别在试验途中验证其冻结状态和融化状态。试验以0、1、3、6、10、15次冻融循环式样为例。

图1 试验所用原状土样以及冻融参照样Fig.1 Undisturbed soil sample for testand reference sample

1.3 动荷载施加方案

试验仪器为GDS动三轴仪,循环荷载采用正弦波形,试验仪器如图2所示。

图2 GDS动三轴仪器舱Fig.2 GDS dynamic tri-axial test instrument

在以往的对于冻土三轴实验研究中,诸多学者选用200 kPa甚至更大的围压,但在该工况中,经计算最大冻结深度所在处围压仅在110 kPa左右。结合试验所用原状土取土深度,试验选用在100 kPa下进行等压排水固结(固结完成的条件以反压体积曲线平稳为准),正弦波频率固定为1 Hz。由于车辆荷载引起的动应力并非双向正弦振动,因此为了保证试样为纯压加载方式,待固结完成后,施加等同于动应力幅值的偏应力,再施加动荷载。按照文献[10]所述，当静偏应力达到预定值后,立刻施加正弦循环荷载，如图3所示,以控制动应力数值不变的方式加载。试验方案如表2所示。

图3 加载方式示意图Fig.3 Schematic diagram of axial load

表2 动三轴试验方案Table 2 Dynamic triaxial test schemes

2 试验结果分析

2.1 累积应变曲线

图4 典型滞回圈曲线示意图Fig.4 Typical hysteresis loop curve diagram

典型滞回圈曲线示意图如图4所示。通过图4可以看出，该类粉质黏土具有很好的黏聚力,即随着振次N的增多,滞回圈越来越瘦小，相邻滞回圈之间的间距也随着振次和应变量的增大而减小，也可以看出滞回圈中应变ε随应力σd的变化存在一定的滞后性，在同一滞回圈中,最大应力所在点并非对应最大应变所在点。且试验加载方式为单向纯压加载,不存在拉拔应力,因此,应取每次循环中应变量最小点作为加载后累积应变进行分析。这并不同于其他相关文献中使用拉压正弦加载方式后,取的偏应力为0时所对应的应变量。根据表2中的试验方案,施加5 000次循环动荷载。试验所得的原状土样在不同动应力σd、不同冻融循环次数n下的累积塑性应变εp与振次N的关系曲线如图5所示。

图5 不同冻融次数下振次与累积应变的关系Fig.5 Relationship between vibration number and accumulated strain under different freeze-thaw cycles

图5中,无论哪一种动应力、冻融循环次数所示的曲线,在加载初期(N≤500),累积塑性应变都会随着N的增加而迅速增加,而当N≥1 000后,其增长速率逐渐减缓且趋于平稳。根据动应力的大小不同,振动前期累积塑性应变变化的速率会随着动应力幅值的增大而增大。N≤500时,图5(a)(σd=20 kPa)所示的累积应变变化程度也明显缓于图5(c)(σd=40 kPa)时的变化程度。文献[11]中提出累积塑性应变的几种不同发展情况有临界型、稳定型(也有其他文献称渐稳型)、破坏型。从图5中可以看出,试验土样受冻融循环后的累积塑性应变曲线均趋于稳定型发展,并未出现破坏现象。由此可以推断,该地区路基原状土的临界动应力要大于试验中所采用的最大动应力幅值。在图5(a)中第10次冻融循环土样的累积应变曲线明显高于第15次冻融循环土样,但曲线形状并未出现其他不同的发展趋势。对于此现象,笔者认为,土样经冻融循环处理时,由于孔隙水结冰后对土样的挤压作用方向、大小无法把控,可能会致使土样内部结构重组咬合,形成偏离基本规律的其他结构特性。文献[12]中也出现了类似的波动现象,需对土样在冻结状态时的微观结构变化状态进行分析。

2.2 冻融次数的影响

为了反映冻融循环次数对累积应变的影响,以冻融循环次数n为横坐标,将振次N为1 000、5 000时的累积塑性应变值εp绘制如图6所示。

根据前文所述,在土样冻结过程中,孔隙水结冰体积膨胀约为9%,对土样内部有挤压作用,且该类路基原状土可塑性良好。因此在挤压作用下,土样内部结构会产生不可逆的塑性变形,使得土中孔隙增大。当土样融化后,因塑性形变导致土样内部结构无法回到土样冻结前的形状。所以在少次冻融循环作用下累积塑性应变变化程度明显。但如此反复作用,经过多次冻融循环后,土体结构中的孔隙度将逐渐适应孔隙水冻胀变化,土样内部结构也渐渐适应了受冻胀后的挤压。从而在相同动荷载作用下,随着冻融循环次数的再次增加,累积塑性应变即使有增加趋势,也不会发生较大的差异。为了更好地阐述此类现象,提出平均增长比计算公式为

(1)

由图6可见，在动应力、振次相同的条件下,εp也会随着冻融循环次数增加而增加。以振次N=5 000时所对应的εp为例,对于不同动应力(20、30、40 kPa)作用下,冻融循环0～6次εp的平均增长比为11.7%、12%、11.2%。冻融循环6～15次土样εp的平均增长比在20、30、40 kPa作用下分别约为0.8%、1.3%、1.3%,平均增长比有明显的减小变化。

笔者认为,试样的累积应变随冻融循环次数的变化在6次冻融以前比较明显,冻融7～10次左右趋于稳定。这类现象在戴文亭等[6]、王静等[12]对于土动强度、动弹性模量的研究结果中也提出了相同的规律。

图6 累积应变随冻融次数的变化Fig.6 Change of cumulative strain with freeze-thaw cycle

3 累积应变模型

3.1 模型的提出

对于经验拟合法,即通过室内试验对数据进行拟合,中外学者在早期就已提出一些简单的指数模型,如Monismith等[13]提出的在早期最常使用的指数模型

εp=aNb

(2)

式(2)中:εp为累积塑性应变；N为振次；a、b为试验拟合系数。

为了对系数a进一步研究,黄茂松等[14]、刘明等[15]先后综合考虑偏应力水平,引入D*,在K0固结状态下对指数模型进行修正，即

εp=a(D*)Nb

(3)

(4)

式中:D*为相对偏应力水平;Dp=(qs+qd)/qult，Ds=qs/qult,二者分别为峰值偏应力水平和静偏应力水平,qult为由修正剑桥模型推导出的极限强度。

考虑其他因素的类似模型还有很多,但都存在一个尚未改变的共性:累积应变εp会随着振次N的增加而难以限制其变化程度。当振次足够大时,模型发展趋势与试验值的稳定性变形特征略有不符。其间,张勇等[16]曾针对该问题进行分析,提出另一种更加稳定的曲线方程，即

(5)

并将a/c赋予累积应变极限值的物理意义。而笔者在试验数据处理时发现:对横坐标振次N取对数,土样经过一定振次后,即使累积塑性应变变化逐渐平稳,但仍然有微小的变形累积,并非绝对稳定，如图7所示,以σd=20 kPa为例。

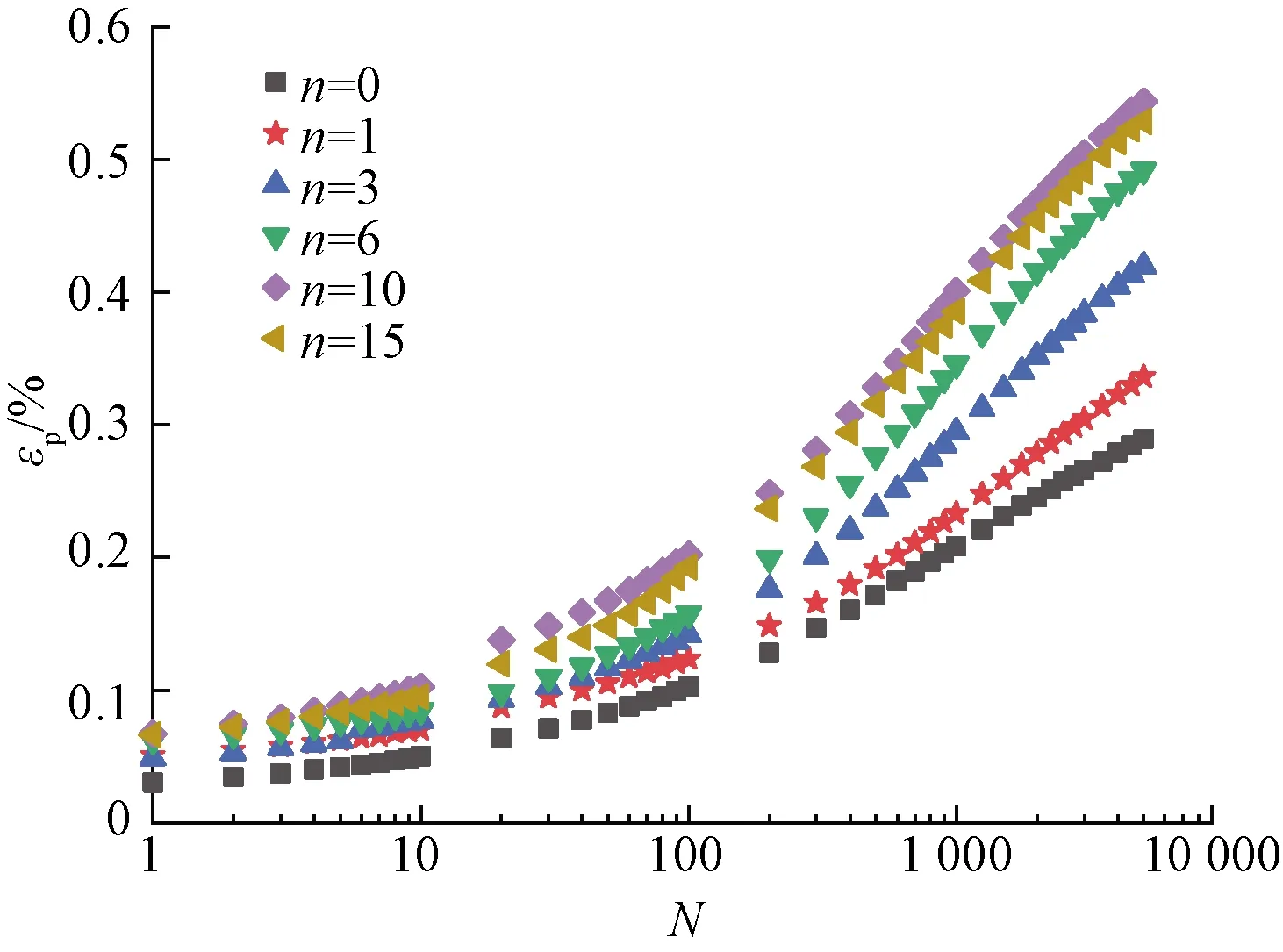
图7 εp-lgN曲线图(σd=20 kPa)Fig.7 Typical curveof εp-lgN(σd=20 kPa)

综合以上模型曲线特征,为了缩减εp随振次N的变化程度,采用式(6)对数方程来拟合εp-N关系曲线，即

εp=a(lgN)b+c

(6)

式(6)中:a为累积应变随振次的变化程度系数；b为拟合函数指数,与试验所用土样性质有关。当N为1时,用参数c修正εp所对应的值,c即为一次震动后的εp。3.2节中将对各参数在不同实验方式下的变化关系进行详细叙述。

图8 不同动应力和冻融次数下拟合效果Fig.8 Fitting effect under different dynamic stress and freeze-thaw cycles

拟合效果如图8所示,各参数拟合以及相关系数Pc如表3所示。

根据洛必达法则推导:

(7)

由曲线的发展规律可知:式(7)中b为常量且大于0。则以此公式类推,该极限值趋于无穷大。证明了在振次足够大的情况下,所用拟合模型中εp随N的变化程度要小于指数模型中的变化程度,更符合试验曲线发展规律。

3.2 拟合参数的变化状态分析

表3中各相关参数在不同动应力作用下随冻融次数的变化关系曲线如图9所示。

由图9可以看出,参数a随着动应力、冻融循环次数的增加而增加,图9(a)中σd=40 kPa所对应的曲线随冻融次数的变化更加明显。b在不同冻融循环次数下变化存在波动,变化程度偏弱,有细微的减小趋势。而c在冻融7～10次后几乎没有变化,也更加证实2.2节所述:试样在经过一定冻融循环后,孔隙的变化会因土样逐渐适应冻融循环变化而趋于稳定。

表3 不同动应力和冻融次数下参数拟合结果Table 3 Fitting results of parameters under different dynamic stress and freeze-thaw cycles

图9 不同实验条件下各参数的变化情况Fig.9 Changes of parameters under different experimental conditions

值得注意的是，在图9(b)3条曲线对比中,当改变动应力的大小时,同一横坐标下,动应力越大参数b越小。这与a、c随动应力幅值的变化趋势呈相反现象。为了更好地阐述参数b随动应力增大而减小这一现象,此处以冻融循环1次后的累积应变曲线为例,如图10所示。

图10 冻融循环1次后不同动应力下累积塑性应变曲线Fig.10 Cumulative plastic strain curve under different dynamic stress in one freeze-thaw cycle

图10中,在动应力幅值为20、30、40 kPa下,对应的试验最终εp分别为0.336%、0.564%、0.889%,其中,振次从1 000～5 000下εp的差值为0.103%、0.124%、0.156%,与试验总应变量的比值分别为30.65%、21.98%、17.54%。由此可知,振次在1 000～5 000次下的Δεp在试验总应变量中所占比重会随着动应力的增大而减小。笔者认为,随着应力幅值的增大,试验中循环荷载对土样的挤压程度也就越大。在土样可承受的动荷载范围内,即当土样未破坏的情况下,所受动荷载越大,土样最后的密实程度就越高，在多次动荷载循环后孔隙度也会越低。因此,动应力越大,前期曲线变化将会越陡峭,曲线后期发展会越平稳[图10(a)],在N取对数后的曲线弯曲程度会越小[图10(b)],拟合函数指数,即参数b的值便相对越小。

4 结论

(1)在不同冻融循环次数、不同动应力下,原状粉质黏土土样的累积塑性应变会随着振次的增加而增加,其增加速率会随着累积应变的增大而逐渐减小,曲线趋于稳定型发展。

(2)同一振次下累积塑性应变随冻融循环次数的增加而增大,增加趋势逐渐平缓。引入平均增长比计算公式,平均增长比在6次冻融循环以前较高,7～10次冻融循环后趋于稳定,且存在有小幅度的波动现象。

(3)通过分析累积塑性应变随振次发展的特点,对该曲线提出了一个新的拟合公式,并且分析不同冻融循环次数对相关拟合参数的影响。参数a、c会随着冻融次数的增加而增大,参数b随着动应力增大而减小。

(4)试验所得曲线均未发生破坏,且随着动应力幅值的增大,曲线在振动后期发展反而比较平稳,因而可以断定在临界动应力以内,该地区土体所受动荷载越大,土体的挤密效应越明显。